Изобретение относится к вычислительной технике и может быть использовано при создании специализированной ЭВМ (специализированного сопроцессора для универсальной ЭВМ), реализующих операции кубического исчисления, используемые в алгоритмах Рота синтеза дискретных устройств (алгоритм извлечения) и синтеза тестов поиска неисправностей (D-алгоритм) схем автоматики и вычислительной техники [см. Миллер Р. Теория переключательных схем. - М.: Наука, 1970. Т. 1; Чжен Г., Мэннинг Е., Метц Г. Диагностика отказов цифровых вычислительных машин. - М.: Мир, 1972; Проектирование цифровых вычислительных машин. Под ред. С.А. Майорова. Учебн. пособ. для вузов. М.: Высшая школа, 1972; Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы). - Л.: Энергия, Ленингр. отд., 1979. - 232 с.; Луцик Ю.А., Лукьянова И.В. Арифметические и логические основы вычислительной техники: Учеб. пособие - Минск: БГУИР, 2004. - 121 с.].
Известно устройство («Ячейка одномерной однородной вычислительной среды») реализации операции d-пересечения [А.с. SU 1173406 А, авторы: Альбеков А.Ш., Герасимов Е.Р., Чикалов А.Н., 1985]. Устройство содержит логические элементы И, ИЛИ, ИЛИ-НЕ, ЗАПРЕТ, восемь входов и семь выходов и реализует таблицу истинности кубической операции d-пересечения [Чжен Г., Мэннинг Е., Метц Г. Диагностика отказов цифровых вычислительных машин. - М.: Мир, 1972]. Недостатком данного устройства является реализация всего одной кубической операции d-пересечения n-мерных кубов.
Известно устройство реализации кубической операции х-произведение [А.с. SU 1656522 А1, авторы: Альбеков А.Ш., Герасимов Е.Р., 1991]. Устройство содержит n вычислительных ячеек, каждая из которых содержит элементы И, ИЛИ-НЕ, ИЛИ, по четыре входа и по три выхода и один решающий узел, содержащий 3n входов, 3n выходов и элементы ИЛИ, ЗАПРЕТ, мажоритарный элемент и реализует таблицу истинности кубической операции х-произведение [Миллер Р. Теория переключательных схем. - М.: Наука, 1970. Т. 1; Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы). - Л.: Энергия, Ленингр. отд., 1979. - 232 с.]. Недостатком данного устройства также является реализация всего одной кубической операции х-произведение n-мерных кубов.
Наиболее близким {прототипом) к патентуемому изобретению является устройство для обработки логической информации, реализующее кубическую операцию склеивания n-мерных кубов [Патент RU 2027218 С1, авторы: Альбеков А.Ш., Герасимов Е.Р., Хализев В.Н., 1995]. Устройство является комбинационным, с жесткой логикой, содержит n вычислительных ячеек, каждая из которых содержит элементы И, ИЛИ-НЕ, ИЛИ, по четыре входа и по три выхода и один решающий блок, содержащий 3n входов, 3n выходов и элементы И, ИЛИ, НЕ, ИСКЛЮЧАЮЩЕЕ ИЛИ и реализует таблицу истинности кубической операции склеивания n-мерных кубов [Миллер Р. Теория переключательных схем. - М.: Наука, 1970. Т. 1; Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы). - Л.: Энергия, Ленингр. отд., 1979. - 232 с.]. Причина, которая не позволяет достичь с помощью аналога того технического результата, который обеспечивается заявляемым изобретением, заключается в невозможности реализации прототипом кубической операции ИЛИ (OR, ∨) из-за жесткости закона его функционирования.
Целью изобретения является расширение функциональных возможностей и производительности специализированной вычислительной техники при реализации ею алгоритмов синтеза дискретных устройств и тестов поиска неисправностей схем автоматики и вычислительной техники. Цель достигается за счет аппаратной реализации кубической операции ИЛИ (OR, ∨).
Техническим результатом изобретения является возможность схемного выполнения заявляемым устройством кубической операции логического сложения ИЛИ (OR, ∨) над двумя n-мерными кубами, n-мерный куб К[1:n] представляет собой вектор, содержащий n координат (компонент), каждая из которых принимает значение на троичном множестве {0, 1, X}.
Операция «кубическое ИЛИ» осуществляется над двумя n-разрядными кубами К1[1:n] и К2[1:n] в соответствии с таблицей истинности табл. 1 [см. studfile.net/preview/7014248/page:5; studall.org/all3-26567.html; dl.nure.ua/plug-infile.php/534/mod_resource/content/2/content/example1.html].
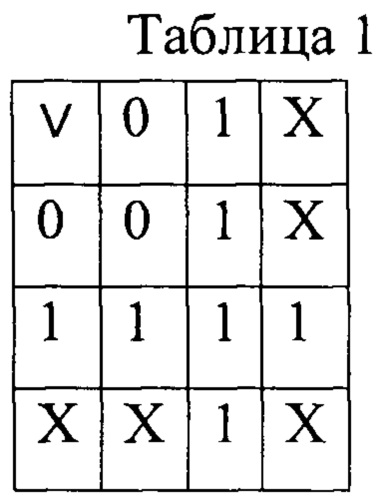
Результатом выполнения операции является n-разрядный куб К3[1:n], координаты которого также определены на троичном множестве {0, 1, X}.
Для практической реализации заявляемого устройства на серийной двоичной элементной базе необходимо осуществить переход от троичной системы счисления к двоичной системе.
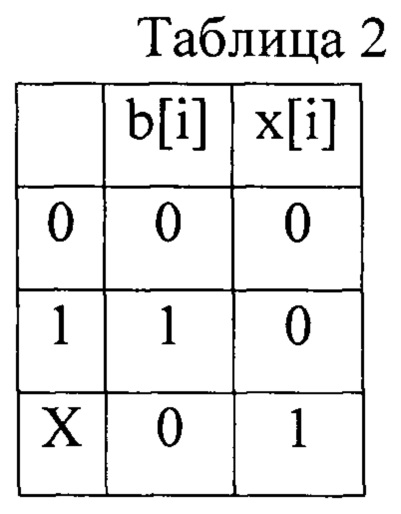
С целью схемного представления троичных значений координат кубов предлагается двухпозиционное представление b[i] и x[i] (табл. 2) координат кубов Кi[1:n], i=1, 2, 3, где b[i] - позиция, кодирующая бинарные значения 0 и 1 из табл. 1; x[i] - позиция, кодирующая значение X из табл. 1.
Поскольку значения координат куба-результата К3[1:n] независимы друг от друга и полностью определяются таблицей истинности (табл. 1), устройство содержит n независимых вычислительных ячеек, каждая из которых реализует табл. 1 с учетом принятой двоичной кодировки (табл. 2) значений координат, и не содержит решающего узла (блока), имеющегося в аналогах. Извлечение из таблиц 1 и 2 аналитических формул логических функций, реализуемых ячейками устройства, дает следующую систему уравнений:
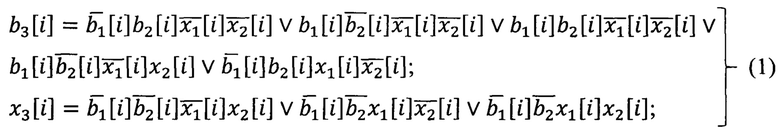
где 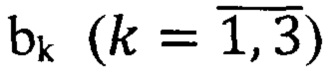 - кодовые значения бинарных (0, 1) координат кубов К1,2,3[1:n],
- кодовые значения бинарных (0, 1) координат кубов К1,2,3[1:n], 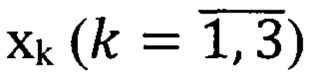 - кодовые значения Х-координат кубов К1,2,3[1:n], i (i=1, 2, …n) - номер кубической координаты.
- кодовые значения Х-координат кубов К1,2,3[1:n], i (i=1, 2, …n) - номер кубической координаты.
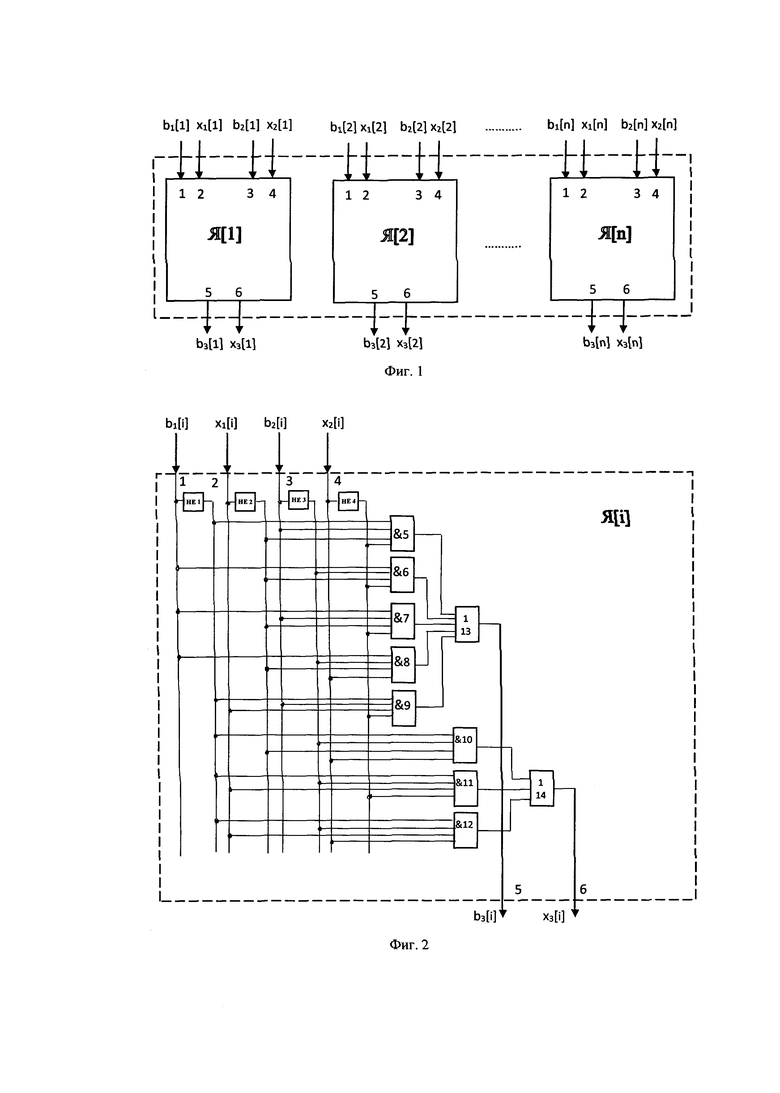
На фиг. 1 представлена структурная схема устройства реализации кубической операции ИЛИ, на фиг. 2 - функциональная схема вычислительной ячейки 1 устройства. Каждая вычислительная ячейка устройства 2, …, 3, как и ячейка 1, реализует систему логических функций (1) и идентична ячейке 1.
Устройство (фиг. 1) содержит n вычислительных ячеек 1, 2, …, 3; 2×n входов, соответствующих координатам куба К1[1:n]; 2×n входов, соответствующих координатам куба К2[1:n]; и 2×n выходов, соответствующих координатам куба-результата К3[1:n].
Вычислительная ячейка 1 устройства (фиг. 2), имеет четыре входа, два выхода и содержит инверторы НЕ 4, 5, 6, 7, четырехвходовые элементы И 8, 9, 10, 11, 12, 14, 15, 16, пятивходовый элемент ИЛИ 13 и трехвходовый элемент ИЛИ 17. Причем, первый вход ячейки соединен с входом элемента НЕ 4, первым входом элемента И 9, первым входом элемента И 10, первым входом элемента И 11. Второй вход ячейки соединен с входом элемента НЕ 5, третьим входом элемента И 12, третьим входом элемента И 15, и третьим входом элемента И 16. Третий вход ячейки соединен с входом элемента НЕ 6, вторым входом элемента И 8, вторым входом элемента И 10, вторым входом элемента И 12. Четвертый вход ячейки соединен с входом элемента НЕ 7, четвертым входом элемента И 11, четвертым входом элемента И 14, четвертым входом элемента И 16. Выход элемента НЕ 4 соединен с первым входом элемента И 8, первым входом элемента И 12, первым входом элемента И 14, первым входом элемента И 15, первым входом элемента И 16. Выход элемента НЕ 5 соединен с третьим входом элемента И 8, третьим входом элемента И 9, третьим входом элемента И 10, третьим входом элемента И 11, третьим входом элемента И 14. Выход элемента НЕ 6 соединен с вторым входом элемента И 9, вторым входом элемента И 11, вторым входом элемента И 14, вторым входом элемента И 15, вторым входом элемента И 16. Выход элемента НЕ 7 соединен с четвертым входом элемента И 8, четвертым входом элемента И 9, четвертым входом элемента И 10, четвертым входом элемента И 12, четвертым входом элемента И 15. Выход элемента И 8 соединен с первым входом элемента ИЛИ 13, выход элемента И 9 соединен с вторым входом элемента ИЛИ 13, выход элемента И 10 соединен с третьим входом элемента ИЛИ 13, выход элемента И 11 соединен с четвертым входом элемента ИЛИ 13, выход элемента И 12 соединен с пятым входом элемента ИЛИ 13, выход которого является первым выходом вычислительной ячейки. Выход элемента И 14 соединен с первым входом элемента ИЛИ 17, выход элемента И 15 соединен с вторым входом элемента ИЛИ 17, выход элемента И 16 соединен с третьим входом элемента ИЛИ 17, выход которого является вторым выходом вычислительной ячейки.
Устройство работает следующим образом. На первые и вторые входы вычислительных ячеек 1, 2, …, 3 подается код куба К1[1:n], на третьи и четвертые входы - код куба К2[1:n]. На выходах вычислительных ячеек вырабатывается код куба К3[1:n]=К1[1:n]∨К2[1:n], являющийся результатом кубической операции ИЛИ. Поскольку ячейки устройства являются комбинационными автоматами, то их работа полностью определена таблицей истинности (табл. 1) с учетом принятого двоичного кодирования (табл. 2) координат {0, 1, X}.
Повышение производительности вычислительного процесса с применением операции кубического ИЛИ, реализуемой заявляемым устройством, из-за за жесткости законов функционирования аналогов, не позволяющей реализовывать кубическое ИЛИ аналогами, доказуемо в сравнении с универсальным программируемым вычислительным устройством последовательной архитектуры. По сравнению с универсальным вычислительным устройством неймановской архитектуры (универсальным процессором) повышение производительности достигается тем, что заявляемое устройство реализует операцию, при условии выставления кодов кубов К1[1:n] и К2[1:n] на его входах, за три машинных такта, в то время, как универсальное устройство, с этой же целью, должно выполнить программный код поразрядной обработки кубов, состоящий из циклической последовательности операторов языка высокого уровня. Поскольку операция «кубическое ИЛИ» определена на 9-ти входных наборах (см. табл. 1), то циклический блок обработки таблицы 1 (напр., на С++) содержит 9 операторов if(), покрывающих все наборы таблицы:

Очевидно, что один оператор if() требует для своей реализации не менее 4-х машинных тактов, а обработка одного разряда кубов К1[1:n], К2[1:n] и К3[1:n] требует, в среднем, выполнения 9/2=4,5 операторов if(). Следовательно, обработка всех разрядов кубов К1[1:n], К2[1:n] и К3[1:n] потребует не менее 4×4,5×n машинных тактов, где n - разрядность обрабатываемых кубов. То есть, выигрыш В по времени реализации кубического ИЛИ заявляемым устройством составит порядка 18×n/3 раз, где n - длина (размерность) обрабатываемых кубов. Так, для n=32, выигрыш составит В≥192 раз, а для n=64, выигрыш составит В≥384 раз.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство реализации операции "КУБИЧЕСКОЕ ИСКЛЮЧАЮЩЕЕ ИЛИ" | 2022 |
|
RU2792603C1 |
| Устройство реализации кубической операции И | 2021 |
|
RU2772311C1 |
| УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ЛОГИЧЕСКОЙ ИНФОРМАЦИИ | 1991 |
|
RU2027218C1 |
| Устройство реализации кубической операции "Дополнение" | 2022 |
|
RU2795382C1 |
| "Устройство реализации операции "/х/-произведение @ -мерных кубов" | 1989 |
|
SU1656522A1 |
| УПРАВЛЯЕМЫЙ МАЖОРИТАРНЫЙ ЭЛЕМЕНТ "ТРИ ИЗ ПЯТИ" | 2017 |
|
RU2651189C1 |
| Многопортовая ячейка оперативного запоминающего устройства | 2017 |
|
RU2665248C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2020 |
|
RU2751802C1 |
| ПОЛНЫЙ ОДНОРАЗРЯДНЫЙ СУММАТОР ПО МОДУЛЮ | 2009 |
|
RU2427027C1 |
| ПОЛНЫЙ ОДНОРАЗРЯДНЫЙ СУММАТОР ПО МОДУЛЮ | 2011 |
|
RU2484519C1 |
Изобретение относится к области вычислительной техники. Технический результат – повышение производительности вычислительной техники при реализации ею алгоритмов синтеза дискретных устройств и тестов поиска неисправностей схем автоматики и вычислительной техники, а также расширение функциональных возможностей, заключающихся в реализации кубической операции ИЛИ. Устройство содержит n вычислительных ячеек. Каждая i-тая 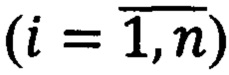 вычислительная ячейка имеет четыре входа, два выхода и содержит четыре элемента НЕ, восемь четырехвходовых элементов И, один пятивходовой элемент ИЛИ и один трехвходовой элемент ИЛИ. За счет оригинального двоичного кодирования троичных значений координат кубов и оригинального соединения входов и выходов элементов вычислительных ячеек, реализуется таблица истинности кубической операции ИЛИ и достигается заявленный технический результат. 2 ил., 2 табл.
вычислительная ячейка имеет четыре входа, два выхода и содержит четыре элемента НЕ, восемь четырехвходовых элементов И, один пятивходовой элемент ИЛИ и один трехвходовой элемент ИЛИ. За счет оригинального двоичного кодирования троичных значений координат кубов и оригинального соединения входов и выходов элементов вычислительных ячеек, реализуется таблица истинности кубической операции ИЛИ и достигается заявленный технический результат. 2 ил., 2 табл.
Устройство реализации кубической операции ИЛИ, содержащее n вычислительных ячеек, где n - размерность куба, причем каждая из n вычислительных ячеек содержит четыре элемента НЕ, восемь четырехвходовых элементов И, один пятивходовой элемент ИЛИ и один трехвходовой элемент ИЛИ, отличающееся тем, что с целью расширения функциональных возможностей за счет реализации операции «кубическое ИЛИ» над n-мерными кубами и с целью повышения производительности вычислений, каждая i-тая 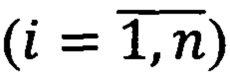 вычислительная ячейка содержит четыре входа и два выхода, причем первый вход i-той ячейки соединен с входом первого элемента НЕ, первым входом второго четырехвходового элемента И, первым входом третьего четырехвходового элемента И, первым входом четвертого четырехвходового элемента И; второй вход ячейки соединен с входом второго элемента НЕ, третьим входом пятого четырехвходового элемента И, третьим входом седьмого четырехвходового элемента И и третьим входом восьмого четырехвходового элемента И; третий вход ячейки соединен с входом третьего элемента НЕ 3, вторым входом первого четырехвходового элемента И, вторым входом третьего четырехвходового элемента И, вторым входом пятого четырехвходового элемента И; четвертый вход ячейки соединен с входом четвертого элемента НЕ, четвертым входом четвертого четырехвходового элемента И, четвертым входом шестого четырехвходового элемента И, четвертым входом восьмого четырехвходового элемента И; выход первого элемента НЕ соединен с первым входом первого четырехвходового элемента И, первым входом пятого четырехвходового элемента И, первым входом шестого четырехвходового элемента И, первым входом седьмого четырехвходового элемента И, первым входом восьмого четырехвходового элемента И; выход второго элемента НЕ соединен с третьим входом первого четырехвходового элемента И, третьим входом второго четырехвходового элемента И, третьим входом третьего четырехвходового элемента И, третьим входом четвертого четырехвходового элемента И, третьим входом шестого четырехвходового элемента И; выход третьего элемента НЕ соединен с вторым входом второго четырехвходового элемента И, вторым входом четвертого четырехвходового элемента И, вторым входом шестого четырехвходового элемента И, вторым входом седьмого четырехвходового элемента И, вторым входом восьмого четырехвходового элемента И; выход четвертого элемента НЕ соединен с четвертым входом первого четырехвходового элемента И, четвертым входом второго четырехвходового элемента И, четвертым входом третьего четырехвходового элемента И, четвертым входом пятого четырехвходового элемента И, четвертым входом седьмого четырехвходового элемента И; выход первого четырехвходового элемента И соединен с первым входом пятивходового элемента ИЛИ, выход второго четырехвходового элемента И соединен с вторым входом пятивходового элемента ИЛИ, выход третьего четырехвходового элемента И соединен с третьим входом пятивходового элемента ИЛИ, выход четвертого четырехвходового элемента И соединен с четвертым входом пятивходового элемента ИЛИ, выход пятого четырехвходового элемента И соединен с пятым входом пятивходового элемента ИЛИ, выход которого является первым выходом вычислительной ячейки; выход шестого четырехвходового элемента И соединен с первым входом трехвходового элемента ИЛИ, выход седьмого четырехвходового элемента И соединен с вторым входом трехвходового элемента ИЛИ, выход восьмого четырехвходового элемента И соединен с третьим входом трехвходового элемента ИЛИ, выход которого является вторым выходом вычислительной ячейки.
вычислительная ячейка содержит четыре входа и два выхода, причем первый вход i-той ячейки соединен с входом первого элемента НЕ, первым входом второго четырехвходового элемента И, первым входом третьего четырехвходового элемента И, первым входом четвертого четырехвходового элемента И; второй вход ячейки соединен с входом второго элемента НЕ, третьим входом пятого четырехвходового элемента И, третьим входом седьмого четырехвходового элемента И и третьим входом восьмого четырехвходового элемента И; третий вход ячейки соединен с входом третьего элемента НЕ 3, вторым входом первого четырехвходового элемента И, вторым входом третьего четырехвходового элемента И, вторым входом пятого четырехвходового элемента И; четвертый вход ячейки соединен с входом четвертого элемента НЕ, четвертым входом четвертого четырехвходового элемента И, четвертым входом шестого четырехвходового элемента И, четвертым входом восьмого четырехвходового элемента И; выход первого элемента НЕ соединен с первым входом первого четырехвходового элемента И, первым входом пятого четырехвходового элемента И, первым входом шестого четырехвходового элемента И, первым входом седьмого четырехвходового элемента И, первым входом восьмого четырехвходового элемента И; выход второго элемента НЕ соединен с третьим входом первого четырехвходового элемента И, третьим входом второго четырехвходового элемента И, третьим входом третьего четырехвходового элемента И, третьим входом четвертого четырехвходового элемента И, третьим входом шестого четырехвходового элемента И; выход третьего элемента НЕ соединен с вторым входом второго четырехвходового элемента И, вторым входом четвертого четырехвходового элемента И, вторым входом шестого четырехвходового элемента И, вторым входом седьмого четырехвходового элемента И, вторым входом восьмого четырехвходового элемента И; выход четвертого элемента НЕ соединен с четвертым входом первого четырехвходового элемента И, четвертым входом второго четырехвходового элемента И, четвертым входом третьего четырехвходового элемента И, четвертым входом пятого четырехвходового элемента И, четвертым входом седьмого четырехвходового элемента И; выход первого четырехвходового элемента И соединен с первым входом пятивходового элемента ИЛИ, выход второго четырехвходового элемента И соединен с вторым входом пятивходового элемента ИЛИ, выход третьего четырехвходового элемента И соединен с третьим входом пятивходового элемента ИЛИ, выход четвертого четырехвходового элемента И соединен с четвертым входом пятивходового элемента ИЛИ, выход пятого четырехвходового элемента И соединен с пятым входом пятивходового элемента ИЛИ, выход которого является первым выходом вычислительной ячейки; выход шестого четырехвходового элемента И соединен с первым входом трехвходового элемента ИЛИ, выход седьмого четырехвходового элемента И соединен с вторым входом трехвходового элемента ИЛИ, выход восьмого четырехвходового элемента И соединен с третьим входом трехвходового элемента ИЛИ, выход которого является вторым выходом вычислительной ячейки.
| УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ЛОГИЧЕСКОЙ ИНФОРМАЦИИ | 1991 |
|
RU2027218C1 |
| Устройство для извлечения кубического корня | 1981 |
|
SU1023323A1 |
| US 4410956 A, 18.10.1983 | |||
| US 5038315 A, 06.08.1991 | |||
| Способ очистки углеводородного сырья от моно-, ди- или полисульфидов или их смесей | 1991 |
|
SU1834898A3 |
Авторы
Даты
2022-09-13—Публикация
2021-07-30—Подача