Изобретение относится к вычислительным модулярным системам и предназначено для выполнения гомоморфного шифрования данных посредством перевода в полиномиальную систему остаточных классов и использует схему Асмута-Блума для обеспечения вычислений над зашифрованными данными.
Необходимость обеспечения безопасности хранения и обработки данных становится особенно актуальными в связи с распространением крупномасштабно распределенных вычислительных инфраструктур, таких как облака. Принимая во внимание, что ни одной отдельной службе хранения и обработки, узлу или пользователю нельзя полностью доверять, конфиденциальные данные должны быть закодированы и распределены по набору независимых узлов хранения. На основе этих фундаментальных принципов был разработан ряд надежных систем хранения, таких как схемы порогового разделения секрета, которые способны защитить данные в облаке, поскольку они потенциально обеспечивают улучшения по сравнению с обычными стратегиями шифрования и репликации, поскольку они не подвержены таким проблемам, как управление ключами и атаки методом грубой силы. При этом важной проблемой остается обработка зашифрованных данных.
Известны способ и устройство обработки отзыва участника, оборудование и носитель информации (патент CN109981293, опубл. 05.07.2019), которые обеспечивают способ обработки отзыва участников. На основе схемы, основанной на цифровой подписи, каждый действительный член в системе управления генерирует секретную долю каждого члена, используя исторический закрытый ключ и случайное число каждого члена; каждый действительный член генерирует новый закрытый ключ, используя других участников и секретные общие ресурсы, полученные действительным участником, весь процесс гарантирует, что открытый ключ группы и закрытый ключ группы по-прежнему остаются неизменными при выходе участников, а открытый ключ группы и закрытый ключ группы по-прежнему может использоваться для подписи и проверки, что снижает стоимость обновления системы; и тем временем, если текущий частный ключ утерян, исторический частный ключ и частный ключ последующего периода не могут быть известны, так что безопасность исторической подписи и последующей подписи также гарантируется. Изобретение дополнительно раскрывает устройство обработки отзыва участников, оборудование обработки отзыва участников и читаемый носитель данных, которые имеют вышеупомянутые положительные эффекты.
Недостатком данного изобретения является невозможность вычисления с зашифрованными данными.
Известны устройство и способ для хранения секретного ключа в гетерогенной избыточной системе (патент CN110430042, опубл. 08.11.2019), которое относится к области гетерогенных избыточных систем и технологии хранения секретных ключей шифрования, в частности к устройству и способу хранения секретного ключа в гетерогенной избыточной системе. Устройство содержит модуль сегментации секретного ключа, используемый для сегментирования секретного ключа определенной длины на m блоков секретных ключей одинаковой длины и маркировки каждого секретного ключевого блока меткой данных 1, 2, ..., m; модуль распределения секретных ключей, используемый для распределения (k-1)⋅m блоков секретных ключей на k блоков хранения секретных ключей в соответствии с установленной стратегией; модуль хранения секретного ключа, используемый для правильного хранения n блоков секретного ключа, выделенных каждому блоку хранения секретного ключа, при этом блоки хранения секретного ключа распределены в различных гетерогенных исполнительных механизмах; и модуль комбинации секретных ключей, используемый для получения блоков секретных ключей из блока хранения секретных ключей и объединения блоков секретных ключей в полный секретный ключ в соответствии с меткой данных. Секретные ключи сегментируются и хранятся в различных блоках хранения секретных ключей, так что все секретные ключи не могут быть потеряны в условиях одноточечного прорыва системы.
Недостатком данного изобретения является невозможность вычисления с зашифрованными данными.
Известна схема разделения секрета с полиномиальным делением над полем GF(Q) (заявка US2010046739, опубл. 25.02.2010), в которой секрет представлен секретным многочленом степени d над GF (q), построенным с помощью простого числа или степени простого числа. Затем секретный многочлен вкладывается в расширенный многочлен степени m, превышающей d. Полином расширения делится на n полиномов-взаимно простых делителей над GF (q) с использованием арифметики, определенной для многочленов над GF (q), для генерации n долей секрета. Каждая доля включает в себя один из полиномов делителей и соответствующий остаток. Эти n общих ресурсов распределяются между множеством взаимодействующих объектов для совместного использования секрета.
Недостатком данного изобретения недостаточная защищенность данных и невозможность вычисления с зашифрованными данными.
Наиболее близким по технической сути является способ и система для безопасного хранения данных с использованием схемы разделения секрета (заявка US2019288841, опубл. 19.09.2019), в котором на основе Китайской теоремы об остатках предоставляется метод безопасного хранения целевого числа. Генерируется набор из n пар взаимно простых чисел, при этом целевое число (секрет) может быть однозначно получено из любого t из n пар. В одном аспекте делители предварительно выбираются так, что любые случайно выбранные n целых чисел из последовательности являются допустимой последовательностью Асмута-Блума для любой структуры доступа (t, n), где 1 <t≤n≤N. В другом аспекте предусмотрены средства для предварительного сохранения членов последовательности Миньотта или Асмута-Блума из N делителей в справочной таблице, из которой могут быть выбраны n делителей. Таким образом поддерживается гибкая структура доступа. Совместное использование секретов для выбранной структуры доступа может быть сгенерировано без необходимости выполнять трудоемкий процесс вычисления последовательностей Миньотта для каждого секрета и структуры доступа. Объем памяти, необходимый для хранения секретных долей, также уменьшается за счет хранения и извлечения пар сравнения в форме индекса и остатка.
Недостатком данного изобретения является сложность выполнения операций с большими числами для получения частей секрета и невозможность вычислений с зашифрованными данными.
Техническим результатом данного изобретения является снижение сложности вычислений за счет применения полиномиальной системы остаточных классов и расширение функциональных возможность, а именно выполнение вычислений над зашифрованными данными.
Технический результат достигается тем, что система гомоморфного шифрования данных на основе системы остаточных классов (СОК), включающая блок шифрования данных, блок дешифрования данных, содержит n блоков шифрования, n блоков нахождения остатков по модулю pj(x), j=1,…,n, вычислительную среду, выполняющую вычисления над зашифрованными данными, нейросетевой блок восстановления, блок дешифрования, при этом в качестве системы остаточных классов взята полиномиальная система остаточных классов с n взаимно простыми многочленами pj(x) над полем F2, для которых k<n является порогом, K(x) – секретный ключ, который взаимно прост с каждым из модулей СОК, Seed(x) - случайный многочлен, удовлетворяющий условию 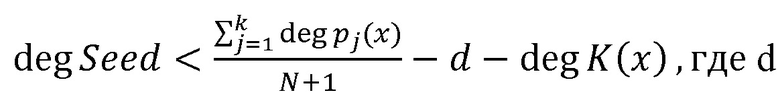 - максимальная степень исходных данных
- максимальная степень исходных данных 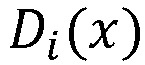 , а N - максимальное количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующих шифрование данных по формуле
, а N - максимальное количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующих шифрование данных по формуле 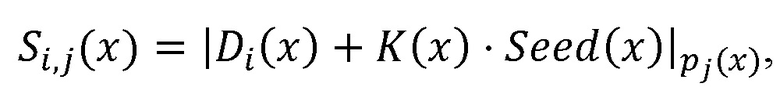 где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены со входами нейросетевого блока восстановления, реализующего формулу
где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены со входами нейросетевого блока восстановления, реализующего формулу 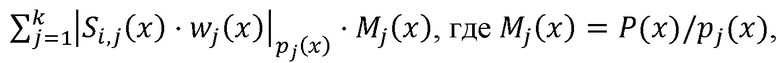
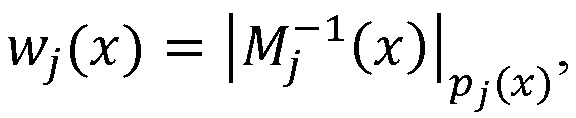 а P(x) - произведение модулей pj(x) принятых k секретов, j=1,…,k, выход нейросетевого блока восстановления соединен со входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы, при этом нейросетевой блок восстановления содержит n нейронных сетей конечного кольца, выполняющих оператор взятия остатка по модулю pj(x) произведения входного значения
а P(x) - произведение модулей pj(x) принятых k секретов, j=1,…,k, выход нейросетевого блока восстановления соединен со входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы, при этом нейросетевой блок восстановления содержит n нейронных сетей конечного кольца, выполняющих оператор взятия остатка по модулю pj(x) произведения входного значения 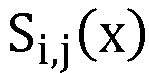 на веса нейронной сети
на веса нейронной сети 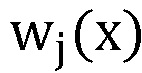 , n блоков умножения многочленов, выполняющих умножение на
, n блоков умножения многочленов, выполняющих умножение на 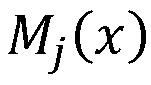 , блок суммирования многочленов, при этом каждый вход нейросетевого блока восстановления подключен к каждому входу нейронных сетей конечного кольца, выходы которых подключены к входам соответствующих блоков умножения многочленов, выходы которых подключены ко входам блока суммирования многочленов, выход которого является выходом нейросетевого блока восстановления.
, блок суммирования многочленов, при этом каждый вход нейросетевого блока восстановления подключен к каждому входу нейронных сетей конечного кольца, выходы которых подключены к входам соответствующих блоков умножения многочленов, выходы которых подключены ко входам блока суммирования многочленов, выход которого является выходом нейросетевого блока восстановления.
Сущность изобретения основана на следующем математическом аппарате. В полиномиальной системе остаточных классов (СОК) число представляется в виде полинома F(x), который в свою очередь представляется как набор остатков
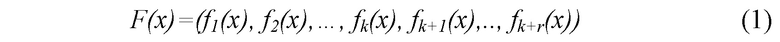
где fi(x)=rest(F(x)/pi(x)), остаток от деления многочленов; pi(x) – взаимно простые многочлены над полем F2, например трехчлены вида pi(x)=x15+xa+1, где a=[1,2,3,4,5,6,7,8,9,11,13,14]. При этом в данной (k,n) схеме разделения секрета используется порог k при разделении секрета на n=k+r частей, т.е. любые k остатков могут восстановить секрет, а менее k остатков уже не могут. Для перехода от двоичного представления к полиномиальному будем ставить в соответствие числу в двоичной системе счисления 10112 многочлен x3+x+1 над F2, т.е. 1 соответствует 1 перед соответствующей степенью. Вычисления над полем F2 соответствуют операции XOR, суммирования по модулю 2. Математический аппарат основан на следующих свойствах:
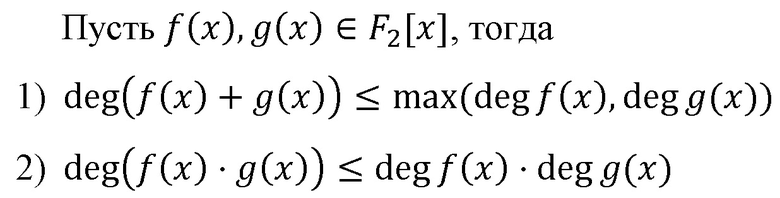
Пусть заданы исходные данные, приведенные к представлению в виде многочленов 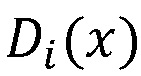 и
и 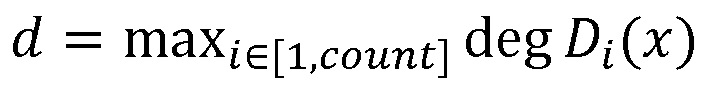 , где
, где 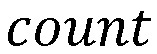 - количество обрабатываемых данных, подлежащих гомоморфному шифрованию, при этом заранее известно, что при гомоморфном шифровании в вычислительной среде будет выполнено не более N умножений с зашифрованными данными. Под вычислительной средой могут пониматься любые ЭВМ, выполняющие вычисления над зашифрованными данными, в том числе, с использованием облачных вычислений. Система гомоморфного шифрования определяется двумя параметрами:
- количество обрабатываемых данных, подлежащих гомоморфному шифрованию, при этом заранее известно, что при гомоморфном шифровании в вычислительной среде будет выполнено не более N умножений с зашифрованными данными. Под вычислительной средой могут пониматься любые ЭВМ, выполняющие вычисления над зашифрованными данными, в том числе, с использованием облачных вычислений. Система гомоморфного шифрования определяется двумя параметрами: 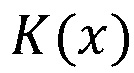 - секретный ключ, взаимно прост с каждым из модулей СОК,
- секретный ключ, взаимно прост с каждым из модулей СОК, 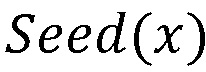 - случайное число, при этом существуют следующие условия: из свойства 1) следует, что количество операций сложения с шифр текстом неограниченно, из свойства 2) и Китайской теоремы об остатках следует, что количество операций умножение с зашифрованными данными ограничено следующим неравенством
- случайное число, при этом существуют следующие условия: из свойства 1) следует, что количество операций сложения с шифр текстом неограниченно, из свойства 2) и Китайской теоремы об остатках следует, что количество операций умножение с зашифрованными данными ограничено следующим неравенством
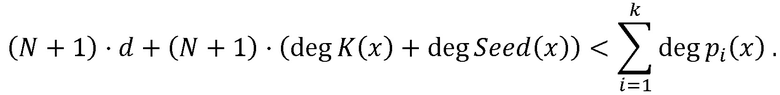
С точки зрения безопасности действует следующее ограничение
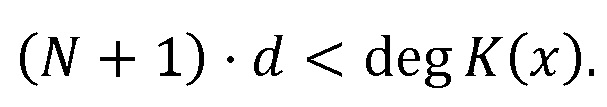
Тогда исходные данные 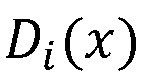 могут быть представлены в виде шифр текстов
могут быть представлены в виде шифр текстов 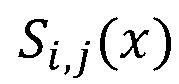 по следующей формуле
по следующей формуле
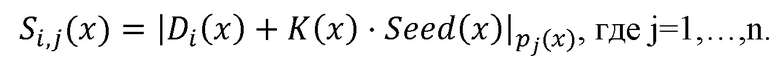
При дешифровании на основе k частей по
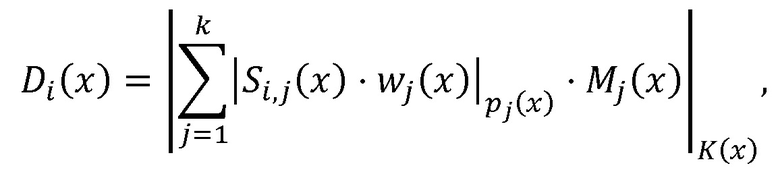
где 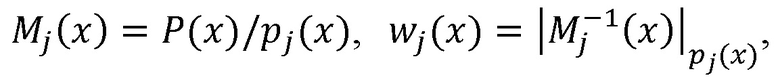 где P(x) - произведение модулей pj(x), j=1,…,k.
где P(x) - произведение модулей pj(x), j=1,…,k.
Изобретение поясняется фигурами 1 и 2.
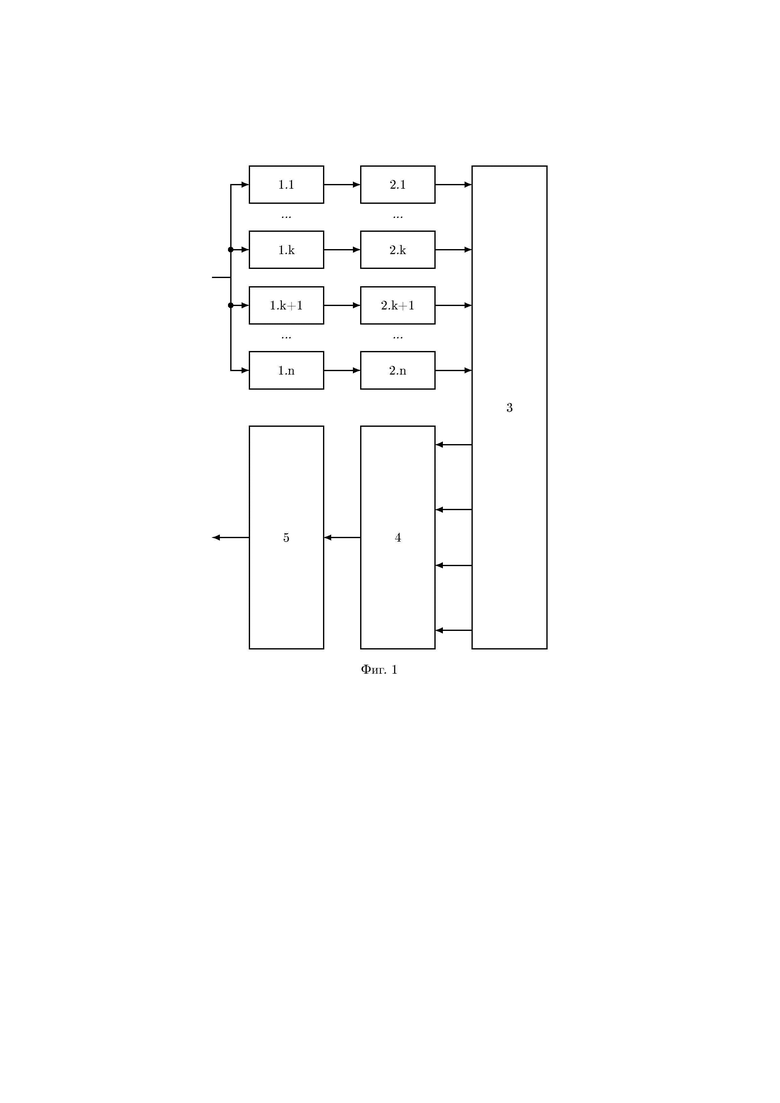
На фигуре 1 изображена общая схема системы гомоморфного шифрования данных на основе системы остаточных классов, содержащая n блоков 1.i шифрования, n блоков 2.i нахождения остатков по модулю pi(x), i=1,…,n, вычислительную среду 3, нейросетевой блок восстановления 4, блок дешифрования 5. Вход системы подключен к входам блоков 1.i шифрования, выходы которых подключены к входам соответствующих блоков 2.i нахождения остатков по модулю pi(x), выходы которых подключены к входам вычислительной среды 3, в которой осуществляется обработка зашифрованных текстов, результат обработки из вычислительной среды 3 поступает на входы нейросетевого блока восстановления 4, выход которого подключен ко входу блока дешифрования 5, выход которого является выходом системы.
Фигура 1 поясняет, но не ограничивает данное изобретение, например, блоки 2.i нахождения остатков по модулю pi(x), реализующий операцию 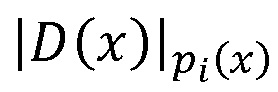 , может быть объединен с блоком 1.i шифрования, реализуя общие вычисления по формуле
, может быть объединен с блоком 1.i шифрования, реализуя общие вычисления по формуле 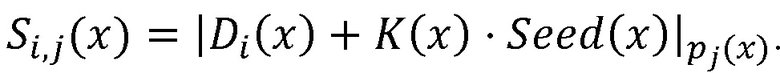
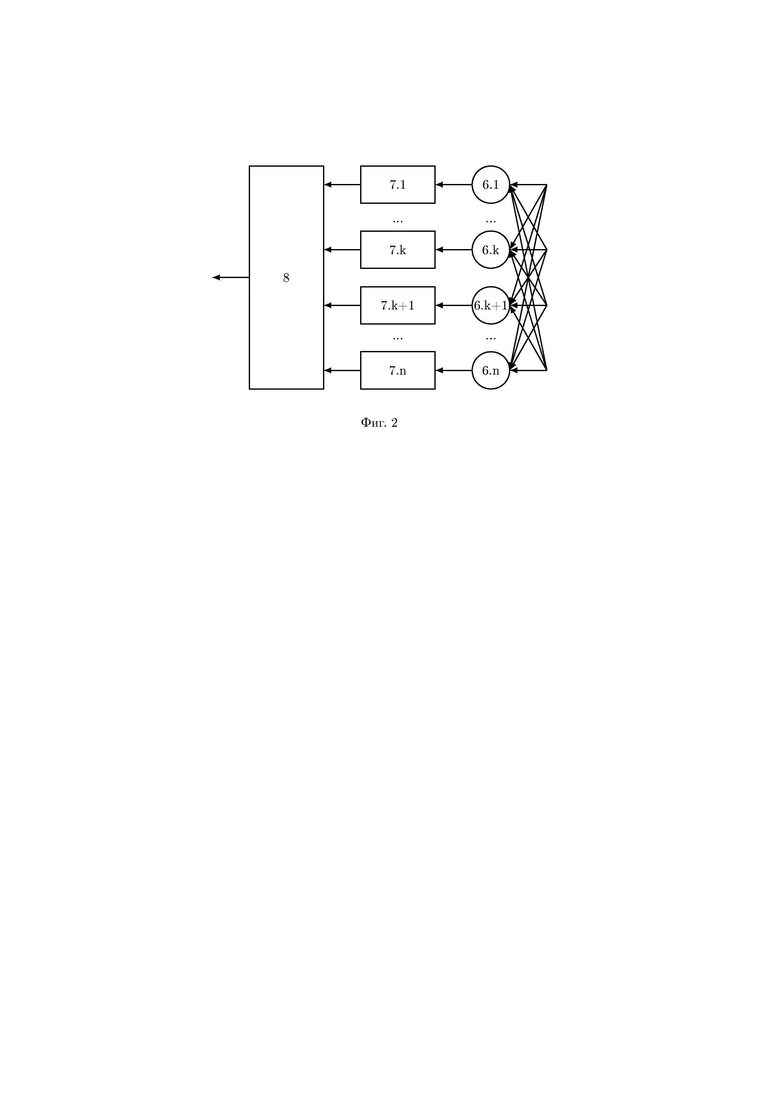
На фигуре 2 раскрыта схема нейросетевого блока восстановления 4, содержащая n нейронных сетей конечного кольца 6.i, выполняющих оператор взятия остатка по модулю pi(x) произведения входного значения 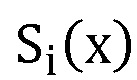 на веса нейронной сети
на веса нейронной сети 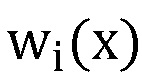 , n блоков умножения многочленов 7.i, выполняющих умножение на
, n блоков умножения многочленов 7.i, выполняющих умножение на 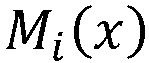 , блок суммирования многочленов 8, при этом каждый вход нейросетевого блока восстановления 4 подключен к каждому входу нейронных сетей конечного кольца 6.i, тем самым сообщая по каким модулям получен секрет для вычисления
, блок суммирования многочленов 8, при этом каждый вход нейросетевого блока восстановления 4 подключен к каждому входу нейронных сетей конечного кольца 6.i, тем самым сообщая по каким модулям получен секрет для вычисления 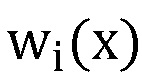 и
и 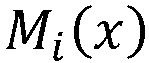 в блоке умножения многочленов 7.i.
в блоке умножения многочленов 7.i.
Рассмотрим пример. Пусть взята полиномиальная система остаточных классов p1=x15+x+1, p2=x15+x2+1, p3=x15+x3+1, p4=x15+x4+1, p5=x15+x5+1, p6=x15+x6+1, p7=x15+x7+1, p8=x15+x8+1, p9=x15+x9+1, p10=x15+x11+1, p11=x15+x13+1, p12=x15+x14+1 с порогом k=10. В качестве секретного ключа задан многочлен K(x)=x49+x+1. Пусть надо произвести вычисления над числами D1(x)=x9+x+1, D2(x)=x16+x+1, вычислим d, получим d=max(deg(D1(x)),deg(D2(x)))=max(9,16)=16. Проверим условие (N+1)⋅d<deg(K(x)), откуда следует, что вычислительная система может выполнять до 2 умножений над зашифрованными данными. Пусть N=1.
Вычислим 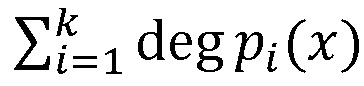 , получим:
, получим:
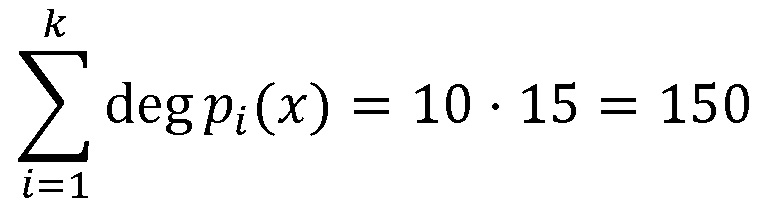 .
.
Вычислим 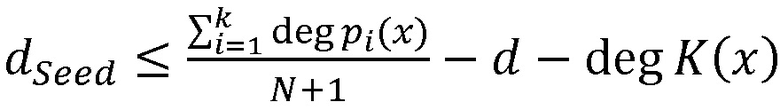 , получим:
, получим:
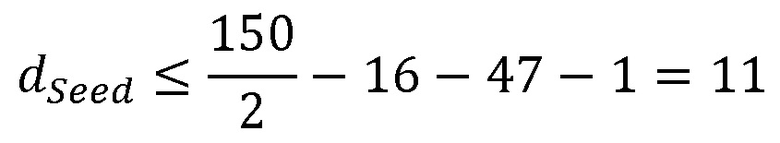 .
.
Пусть 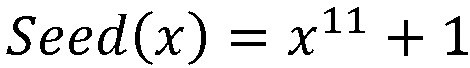 при кодировании
при кодировании 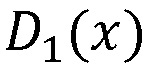 , тогда в блоках 1.j шифрования и блоках 2.j нахождения остатков по модулю pj(x) получают следующие значения
, тогда в блоках 1.j шифрования и блоках 2.j нахождения остатков по модулю pj(x) получают следующие значения 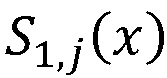 , которые совместно со значением модуля pj(x) передаются в вычислительную среду 3:
, которые совместно со значением модуля pj(x) передаются в вычислительную среду 3:
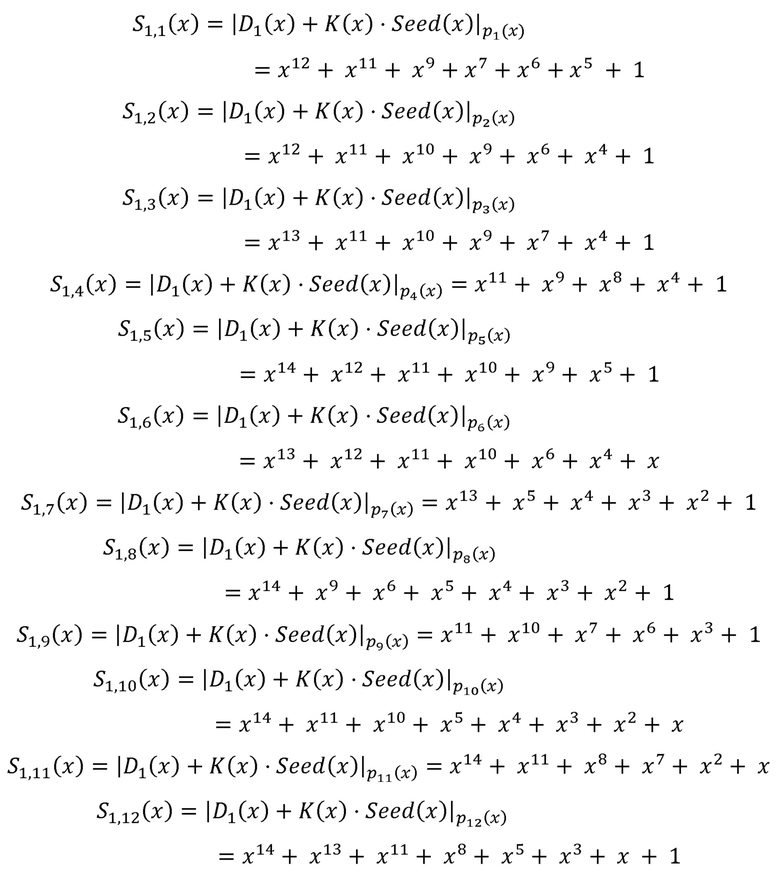
Пусть  при кодировании
при кодировании  , тогда в блоках 1.j шифрования и блоках 2.j нахождения остатков по модулю pj(x) получают следующие значения
, тогда в блоках 1.j шифрования и блоках 2.j нахождения остатков по модулю pj(x) получают следующие значения , которые совместно со значением модуля pj(x) передаются в вычислительную среду 3:
, которые совместно со значением модуля pj(x) передаются в вычислительную среду 3:

Пусть в вычислительной среде 3 выполняется сложение зашифрованных чисел. Получим

Пусть для восстановления из вычислительной среды 3 получено 10 частей из 12, и поскольку порог равен 10, то этого достаточно для восстановления. Пусть для простоты получены результаты по первым 10 модулям, т.е. R1(x)-R10(x). Данные значения с соответствующими модулями поступают в нейросетевой блока восстановления 4.
В нейронной сети конечного кольца 6.1 на основе принятых значений модуля находятся значения
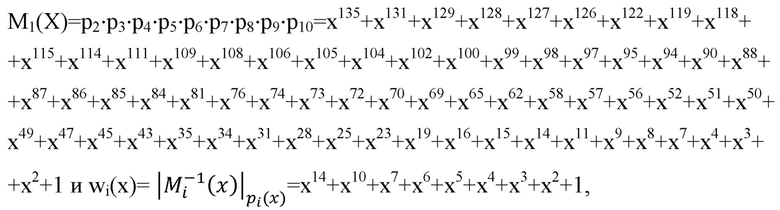
тогда на выходе нейронной сети конечного кольца будет значение
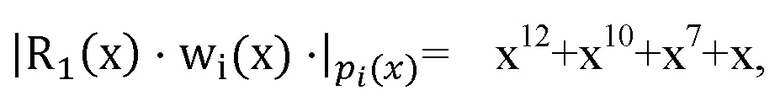
которое поступает на вход блока умножения многочленов 7.1, выполняющий умножение на 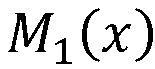 , и подающий на свой выход, который является входом блока суммирования многочленов 8, значение
, и подающий на свой выход, который является входом блока суммирования многочленов 8, значение 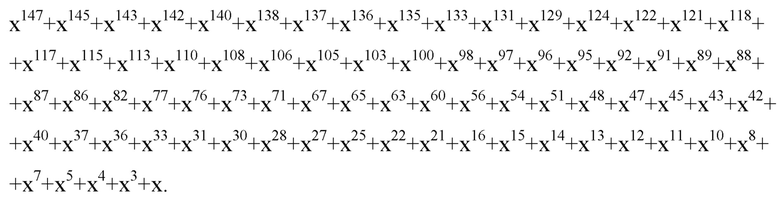
Аналогичные вычисления проводятся в остальных блоках 6.i и 7.i. В случае, когда данные по этим модулям не приняты, значения принимаются равными 0.
Таким образом, на выходе блока суммирования многочленов 8 получим зашифрованный результат сложения x60+x58+x50+x16+x12+x11+x10+x2+x.
В блоке дешифрования 5 находится остаток по секретному ключу K(x).
(x60+x58+x50+x16+x12+x11+x10+x2+x) mod (x49+x+1)= x16+x9.
Проведем проверку, сложив в поле F2[x] значения D1(x)=x9+x+1, D2(x)=x16+x+1, получим x16+x+1+ x9+x+1= x16+x9.
Таким образом, заявляемая система позволяет производить вычисления над зашифрованными числами.
Преимуществом данного устройства является выполнение операций над полем 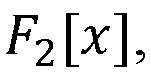 что позволяет производить вычисления с использованием логического элемента XOR, а также возможность выполнения операций над зашифрованными числами.
что позволяет производить вычисления с использованием логического элемента XOR, а также возможность выполнения операций над зашифрованными числами.
Реализация всего устройства возможна с использованием программируемых логических интегральных схем (ПЛИС), специализированных интегральных схем, а также в виде алгоритма работы ЭВМ и может использоваться как отдельное устройство, так и как сопроцессор для выполнения гомоморфного шифрования данных на основе системы остаточных классов.
| название | год | авторы | номер документа |
|---|---|---|---|
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| Способ защиты информации в облачных вычислениях с использованием гомоморфного шифрования | 2017 |
|
RU2691874C2 |
| ИСПОЛЬЗОВАНИЕ ИЗОГЕНИЙ ДЛЯ РАЗРАБОТКИ КРИПТОСИСТЕМ | 2004 |
|
RU2376651C2 |
| Способ и устройство шифрования данных | 2021 |
|
RU2763394C1 |
| РАСПРЕДЕЛЕНИЕ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ СОСТАВНЫХ ПОВТОРНО ЗАШИФРОВАННЫХ ИЗОБРАЖЕНИЙ | 2021 |
|
RU2828473C1 |
| РАСПРЕДЕЛЕНИЕ ИЗОБРАЖЕНИЙ С СОХРАНЕНИЕМ ПРИВАТНОСТИ | 2021 |
|
RU2826373C1 |
| ВОССТАНОВЛЕНИЕ ЗАШИФРОВАННОЙ ИНФОРМАЦИИ ТРАНЗАКЦИЙ В КОНФИДЕНЦИАЛЬНЫХ ТРАНЗАКЦИЯХ С ЦЕПОЧКАМИ БЛОКОВ | 2018 |
|
RU2726157C1 |
| СПОСОБ ФОРМИРОВАНИЯ ОБЩЕГО СЕКРЕТНОГО КЛЮЧА В ГРУППЕ АБОНЕНТОВ | 2019 |
|
RU2719634C1 |
| СИСТЕМА И СПОСОБ ДЛЯ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2721959C1 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО С ИЗМЕНЯЕМОЙ КОНФИГУРАЦИЕЙ | 2018 |
|
RU2752697C1 |
Изобретение относится к вычислительным модулярным системам и предназначено для выполнения гомоморфного шифрования данных. Техническим результатом является снижение сложности вычислений за счет применения полиномиальной системы остаточных классов и возможность выполнения вычислений над зашифрованными данными. Система гомоморфного шифрования данных на основе системы остаточных классов (СОК), включающая блок шифрования данных, блок дешифрования данных, содержит n блоков шифрования, n блоков нахождения остатков по модулю pj(x), j=1, …, n, вычислительную среду, выполняющую вычисления над зашифрованными данными, нейросетевой блок восстановления, блок дешифрования, при этом в качестве системы остаточных классов взята полиномиальная система остаточных классов с n взаимно простыми многочленами pj(x) над полем F2, для которых k<n является порогом, K(x) – секретный ключ, который взаимно прост с каждым из модулей СОК, Seed(x) - случайный многочлен, удовлетворяющий условию 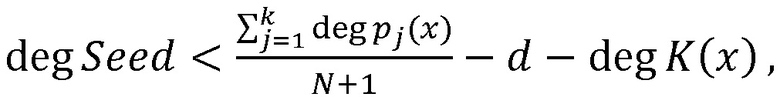 где d - максимальная степень исходных данных
где d - максимальная степень исходных данных 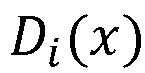 , а N - количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующие шифрование данных по формуле
, а N - количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующие шифрование данных по формуле 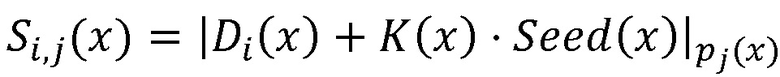 , где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены с входами нейросетевого блока восстановления, реализующего формулу
, где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены с входами нейросетевого блока восстановления, реализующего формулу 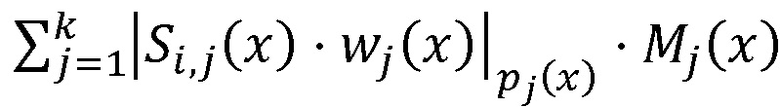 , где
, где 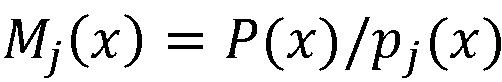 ,
, 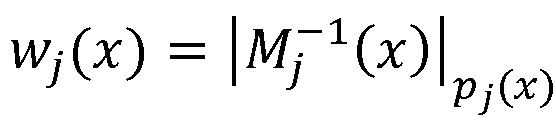 , а P(x) - произведение модулей pj(x), j=1, …, k, выход нейросетевого блока восстановления соединен со входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы. 2 ил.
, а P(x) - произведение модулей pj(x), j=1, …, k, выход нейросетевого блока восстановления соединен со входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы. 2 ил.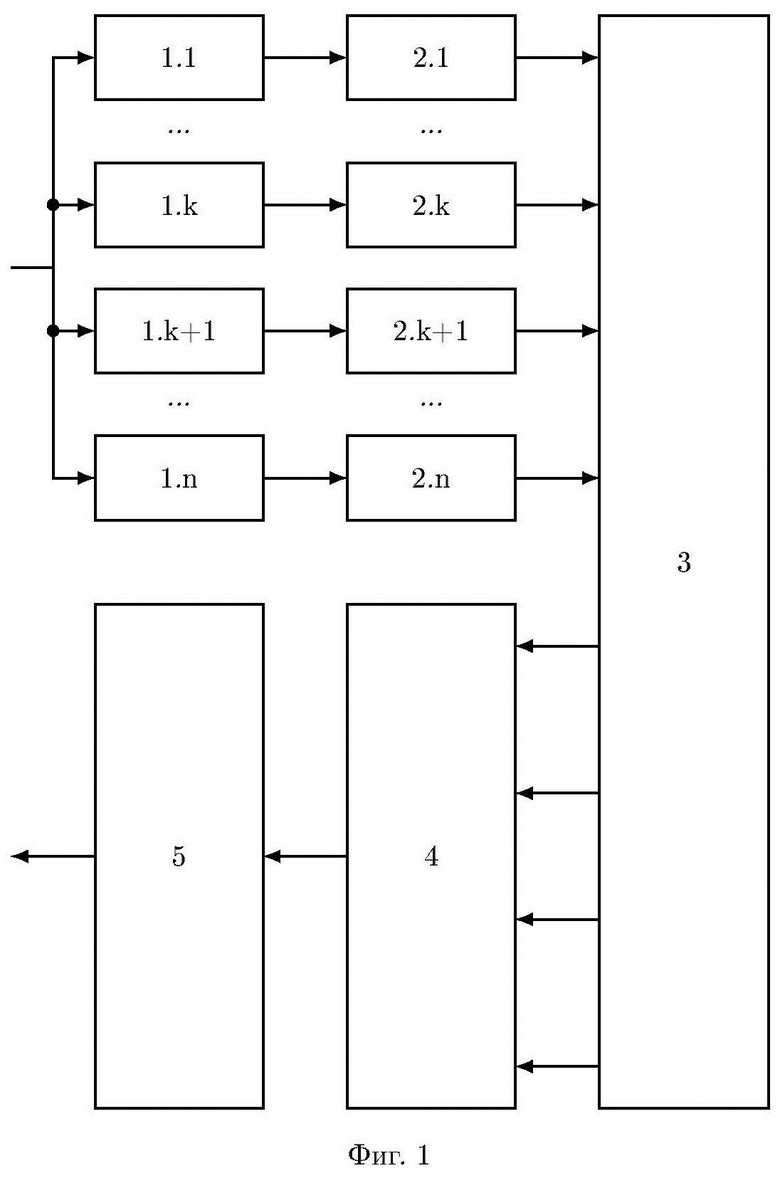
Система гомоморфного шифрования данных на основе системы остаточных классов (СОК), включающая блок шифрования данных, блок дешифрования данных, отличающаяся тем, что содержит n блоков шифрования, n блоков нахождения остатков по модулю pj(x), j = 1, …, n, вычислительную среду, выполняющую вычисления над зашифрованными данными, нейросетевой блок восстановления, блок дешифрования, при этом в качестве системы остаточных классов взята полиномиальная система остаточных классов с n взаимно простыми многочленами pj(x) над полем F2, для которых k<n является порогом, K(x) - секретный ключ, который взаимно прост с каждым из модулей СОК, Seed(x) - случайный многочлен, удовлетворяющий условию 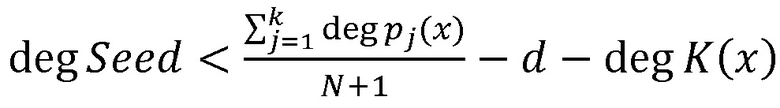 , где d - максимальная степень исходных данных
, где d - максимальная степень исходных данных 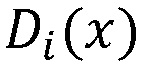 , а N - максимальное количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующих шифрование данных по формуле
, а N - максимальное количество операций умножения с зашифрованными данными, исходные данные поступают через блоки шифрования на входы соответствующих блоков нахождения остатков по модулю pj(x), совместно реализующих шифрование данных по формуле 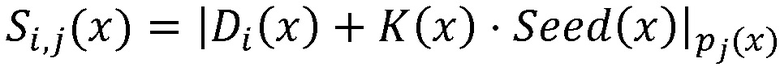 , где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены с входами нейросетевого блока восстановления, реализующего формулу
, где i - номер исходных данных, выходы блоков нахождения остатков по модулю pj(x) соединены с входами вычислительной среды, выходы которой соединены с входами нейросетевого блока восстановления, реализующего формулу 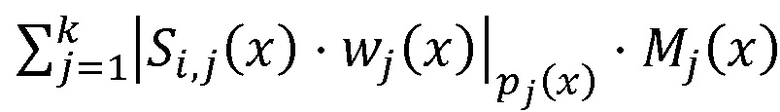 , где
, где 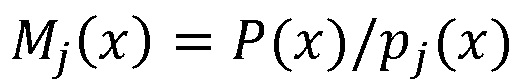 ,
, 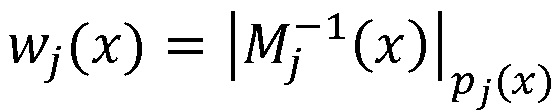 , а P(x) - произведение модулей pj(x) принятых k секретов, j = 1, …, k, выход нейросетевого блока восстановления соединен с входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы, при этом нейросетевой блок восстановления содержит n нейронных сетей конечного кольца, выполняющих оператор взятия остатка по модулю pj(x) произведения входного значения
, а P(x) - произведение модулей pj(x) принятых k секретов, j = 1, …, k, выход нейросетевого блока восстановления соединен с входом блока дешифрования, осуществляющего нахождение остатка по секретному ключу K(x), выход блока дешифрования является выходом системы, при этом нейросетевой блок восстановления содержит n нейронных сетей конечного кольца, выполняющих оператор взятия остатка по модулю pj(x) произведения входного значения 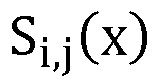 на веса нейронной сети
на веса нейронной сети 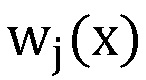 , n блоков умножения многочленов, выполняющих умножение на
, n блоков умножения многочленов, выполняющих умножение на 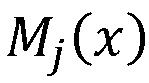 , блок суммирования многочленов, при этом каждый вход нейросетевого блока восстановления подключен к каждому входу нейронных сетей конечного кольца, выходы которых подключены к входам соответствующих блоков умножения многочленов, выходы которых подключены к входам блока суммирования многочленов, выход которого является выходом нейросетевого блока восстановления.
, блок суммирования многочленов, при этом каждый вход нейросетевого блока восстановления подключен к каждому входу нейронных сетей конечного кольца, выходы которых подключены к входам соответствующих блоков умножения многочленов, выходы которых подключены к входам блока суммирования многочленов, выход которого является выходом нейросетевого блока восстановления.
| Станок для придания концам круглых радиаторных трубок шестигранного сечения | 1924 |
|
SU2019A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| CN 109981293 A, 05.07.2019 | |||
| CN 110430042 A, 08.11.2019 | |||
| 0 |
|
SU163440A1 | |
| 0 |
|
SU161050A1 | |
Авторы
Даты
2022-09-19—Публикация
2021-12-27—Подача