ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к сетевому узлу, выполненному для осуществления криптографической операции, способу осуществления криптографической операции и компьютерочитаемому носителю информации.
УРОВЕНЬ ТЕХНИКИ
В криптографии протокол выработки общего ключа представляет собой протокол, посредством которого две или более сторон, которые, возможно, еще не используют совместно общий ключ, могут согласовывать такой ключ. Предпочтительно обе стороны могут влиять на результат, чтобы ни одна из сторон не могла принуждать к выбору ключа. Злоумышленных, который перехватывает обмен данными между двумя сторонами, не должен ничего узнать о ключе. Тем не менее, хотя злоумышленник, который видит тот же обмен данными, узнает немного или ничего, сами стороны могут извлекать совместно используемый ключ. Протоколы выработки общего ключа полезны, например, для защиты связи, например, для шифрования и/или проверки подлинности сообщений между сторонами.
Для способствования защищенной связи между сторонами протоколы выработки общего ключа иногда дополнительно подразделяют на схемы обмена криптографическими ключами (KEX) и инкапсуляции криптографического ключа (KEM).
Схемы KEX могут включать обмен открытыми ключами каждой стороной, которые затем независимо используются другой стороной наряду с их собственными секретным ключом для вычисления общего совместного ключа. Хорошо известным примером такой схемы KEX является обмен ключами Диффи-Хеллмана, защищенность которого основана на решении задачи дискретного логарифмирования. Интересной особенностью некоторых схем KEX является то, что стороны не обмениваются никогда фактическим конечным общим секретом, даже в зашифрованном виде, а две стороны вычисляют его независимо на каждом конце. В результате достигают требуемого свойства, известному как прямая секретность, которое гарантирует, что даже вскрытие злоумышленником долгосрочного секретного ключа какой-либо стороны в будущем не поставит под угрозу секретность зашифрованных сообщений, которыми обменивались в прошлом.
Схемы KEM могут устанавливать общий секрет между двумя объектами или сторонами за счет использования одной стороной, обычно инициатором обмена данными, асимметричной криптографии для шифрования или инкапсуляции (с помощью открытого ключа другой стороны) и передачи общего ключа другой стороне, называемой ответчиком, которая может после этого расшифровывать или декапсулировать его (с помощью своего секретного ключа) и затем использовать для защищенного обмена данными со стороной-инициатором. Такие схемы KEM могут только достигать прямой секретности, если она кратковременная. В противном случае любой злоумышленник, который вскрывает секретной ключ какой-либо стороны для прошлого сеанса и записал все сообщения, которыми обменивались стороны в этом сеансе, может восстановить общий секрет для данного конкретного сеанса.
Ввиду растущего спроса на безопасность в Интернете вещей схемы обмена ключами должны также достигать высокой эффективности (т. е. требований к минимальному объему обмена данными или пропускной способности), оставаясь при этом надежными против классических, а также обладающих квантовыми возможностями злоумышленников.
Последние достижения указывают на то, что квантовые компьютеры могут стать реальностью через несколько лет. Возможно, в течение каких-то 5-10 лет. Как только квантовый компьютер будет доступным, большинство существующих криптографических схем с открытым ключом станут ненадежными, т. к. основополагающие задачи, на которых они основаны, могут быть эффективно решены квантовым компьютером. Следовательно, крайне важно разработать квантово-устойчивые алгоритмы с открытым ключом, т. е. алгоритмы с открытым ключом, которые не могут быть взломаны при помощи квантового компьютера.
Существуют несколько классов квантово-устойчивых алгоритмов: на основе теории решеток, на основе кода, на основе изогении и т. д. В настоящем документе мы имеем дело с квантово-устойчивыми алгоритмами на основе теории решеток. Основанные на решетках криптографические системы являются активной областью исследований, в которой были предложены множество различных типов систем. Например, решетка может быть определена в виде матрицы чисел, например, элементов некоторого конечного поля, или с использованием полинома и т. д. Тип криптографической операции тоже может меняться. Например, основанная на решетках криптография доступна для: инкапсуляции ключа (KEM), обмена ключами (KEX), шифрования с открытым ключом (PKE), цифровых подписей и т. д. Примерами этих схем являются:
основанный на LWE KEX, такой как Frodo;
основанные на RLWE KEX и CPA-KEM Newhope и NewHopeSimple;
основанные на модульной решетке CPA-PKE, CPA-KEM и CCA-KEM, такие как Kyber;
основанный на LWR KEX,такой как spKEX.
Каждая из вышеуказанных схем реализует криптографический протокол (например, KEX, KEM или PKE), опирающийся на одну основополагающую задачу, например, обучение с ошибками (LWE), или обучение с округлением (LWR), модульные решетки с модулями, например, RLWE для фиксированного кольца, или LWR. Например: NewHope опирается только на RLWE, Kyber опирается только на объединение модулей k = 3 причем каждый модуль является многочлен в кольце Zq[x]/x256 + 1, spKEX опирается только на LWR, Frodo опирается только на LWE. В схемах, таких как RLWE, R означает «кольцо» или реализации полиномиального типа.
Это создает несколько проблем. Прежде всего, реализация каждой из таких систем будет крупным капиталовложением. Нужно будет не только закодировать каждую из схем, но и отладить каждую, чтобы убедиться в отсутствии критических ошибок, которые могут ухудшать их безопасность. С другой стороны, реализация не всех схем, или по меньшей мере большинства, тоже влечет определенные риски. Если одна из вышеуказанных задач взломана, например, RLWE или модульная решетка, то все соответствующие схемы полностью взломаны. Желательно наличие некоторого варианта обновления, чтобы в случае взлома можно было перейти с одного типа схемы на другой.
Литература
[1] «Device and method sharing a matrix for use in a cryptographic protocol», заявка на европейский патент № 17159296.7, поданная 6 марта 2017 г. № в реестре поверенного: 2017P01555
[2] Ludo Tolhuizen, Ronald Rietman and Oscar Garcia-Morchon, «Improved key reconciliation method», Cryptology ePrint Archive, Report 2017/295, https://eprint.iacr.org/2017/295
[3] (Frodo): J. Bos et al, «Frodo: Take off the ring! Practical, Quantum-Secure Key Exchange from LWE», Cryptology ePrint Archive, Report 2016/659, https://eprint.iacr.org/2016/659
[4] (New Hope): E. Alkim et al, «Post-quantum key exchange - a new hope», Cryptology ePrint Archive, Report 2015/192, https://eprint.iacr.org/2015/1092
[5] (New Hope Simple): E. Alim et al, «NewHope without reconciliation», Cryptology ePrint Archive, Report 2016/1157, https://eprint.iacr.org/2016/1157
[6] (Kyber): J. Bos et al, «CRYSTALS -- Kyber: a CCA-secure module-lattice-based KEM», Cryptology ePrint Archive, Report 2017/634, https://eprint.iacr.org/2017/634
[7] (spKEX): S. Bhattacharya et al, «spKEX: an optimized lattice-based key exchange», Cryptology ePrint Archive, Report 2017/709, https://eprint.iacr.org/2017/709
Каждый из документов [1]-[7] включен в настоящий документ путем ссылки.
РАСКРЫТИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Авторы изобретения поняли, что можно определить одну схему, которая параметризует большие классы криптографии, основанной на решетках, принимая лишь несколько входных параметров, которые изменяют характер лежащей в основе криптографии. Например, криптографическое устройство, которое определено в формуле изобретения, может принимать параметр (d) сложности и параметр (n) структуры, которых вместе достаточно для задания типа используемой криптографии. Как параметр (d) сложности, так и параметр (n) структуры представляют собой положительные целые числа. При повышении параметра сложности структура задачи остается той же самой, но более крупной, и, таким образом, используются более стойкие реализации. Параметр сложности иногда называют параметром безопасности. В варианте реализации параметр сложность относится к размеру лежащей в основе решетки. Чем больше значение параметра сложности, тем больше размер лежащей в основе решетки, и, следовательно, тем труднее решить задачу злоумышленнику. Параметр структуры относится к величине алгебраической структуры в системе. Чем выше значение параметра структуры, тем больше алгебраическая структура. Предполагается, что при более высоких значениях параметра структуры атаковать может быть легче, поскольку решетка имеет больше закономерностей. Например, в случае продвижения исследований по поиску все более хорошего способа решения задач теории решеток пользователь может реагировать увеличением параметра сложности. С другой стороны, в случае продвижения исследований по поиску радикально более хорошего способа решения задачи теории решеток конкретного типа пользователь может реагировать уменьшением параметра структуры.
Например, в варианте реализации определяют схему, которая может эффективно реализовывать множества лежащих в основе задач, а именно: RLWE, RLWR, модульное RLWE, модульное RLWR, LWE и LWR. Это означает не то, что схема опирается на две разные спецификации, одну для задачи 1 и другую для задачи 2, а то, что один и тот же алгоритм может быт использован для реализации обоих задач, причем единственным отличием являются входные параметры. Преимущества:
- охват множества потенциальных областей применения с помощью одной и той же схемы;
- сведение к минимуму затрат на реализацию;
- уменьшение размера кода;
- подготовка к потенциальному сценарию перехода, в котором опора на «более слабую» задачу больше ненадежна и требуются новые алгоритмы, опирающиеся на «более стойкую» задачу.
Криптографическое устройство представляет собой электронное устройство. Например, криптографическое устройство может быть мобильным электронным устройством, например мобильным телефоном. Например, криптографическое устройством может быть телеприставкой, смарт-картой, компьютером и т. д. Способ выполнения криптографической операции, описанный в настоящем документе, может быть применен к широкому диапазону областей практического применения. В число таких областей практического применения входят финансовые приложения, конфиденциальная или аутентифицированная связь и т. д.
Способ согласно настоящему изобретению может быть реализован на компьютере в виде компьютеризованного способа, или в виде специализированного оборудования, или в виде сочетания того и другого. Исполнимый код для способа в согласно настоящему изобретению может храниться в компьютерном программном продукте. В число примеров компьютерных программных продуктов входят запоминающие устройства, оптические запоминающие устройства, интегральные схемы, серверы, интерактивное программное обеспечение и т. д. Предпочтительно компьютерный программный продукт содержит некратковременный программных код, хранящийся на компьютерочитаемом носителе информации, для осуществления способа в соответствии с настоящим изобретением при исполнении данного программного продукта на компьютере.
В предпочтительном варианте реализации компьютерная программная программа представляет собой компьютерный программный код, выполненный с возможностью осуществления всех этапов способа в соответствии с настоящим изобретением при выполнении компьютерной программы на компьютере. Предпочтительно компьютерную программу реализуют на компьютерочитаемом носителе информации.
Согласно другому аспекту настоящего изобретения предложен способ создания компьютерной программы, доступной для загрузки. Этот аспект используют при загрузке компьютерной программы, например, в App Store компании Apple, Play Store компании Google или Windows Store компании Microsoft, а также в том случае, когда компьютерная программа доступна для загрузки из такого магазина.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Дальнейшие подробные сведения, аспекты и варианты реализации будут описаны только на примерах со ссылкой на чертежи. Элементы на фигурах показаны для простоты и ясности и необязательно изображены в масштабе. На фигурах элементы, которые соответствуют уже рассмотренным элементам, могут иметь одинаковые ссылочные позиции. Содержание чертежей:
на Фиг. 1 схематически показан пример варианта реализации сети с выработкой общего ключа;
на Фиг. 2 схематически показан пример варианта реализации способа электронного обмена ключами;
на Фиг. 3a схематически показан компьютерочитаемый носитель информации, имеющий выполненную с возможностью записи часть, содержащую компьютерную программу согласно настоящему варианту реализации,
на Фиг. 3b схематически показано представление процессорной системы согласно варианту реализации,
на Фиг. 4a схематически показан пример варианта реализации узла расшифрования с открытым ключом,
на Фиг. 4b схематически показан пример варианта реализации узла с шифрованием открытого ключа.
Список номеров позиций на Фиг. 1 и Фиг. 3:
100 сеть с выработкой общего ключа
110 сетевой узел типа инициатора
120 интерфейс связи
130 блок общей матрицы
131 параметр сложности и параметр структуры
140 блок матрицы закрытого ключа
150 блок матрицы открытого ключа
160 блок общего ключа
162 необработанный ключ
164 данные согласования (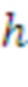 )
)
166 общий ключ
210 сетевой узел типа ответчика
220 интерфейс связи
230 блок общей матрицы
240 блок матрицы закрытого ключа
250 блок матрицы открытого ключа
260 блок общего ключа
262 необработанный ключ
264 данные согласования (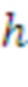 )
)
266 общий ключ
1000 компьютерочитаемый носитель информации
1010 выполненная с возможностью записи часть
1020 компьютерная программа
1110 интегральная (-ые) схема (-ы)
1120 блок обработки
1122 память
1124 специализированная интегральная схема
1126 элемент связи
1130 межсоединение
1140 процессорная система
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Хотя настоящее изобретение может быть реализовано во многих различных формах, на чертежах показаны и будут подробно описаны один или более конкретных вариантов реализации при том понимании, что настоящее описание нужно рассматривать как пример принципов настоящего изобретения, и оно не предназначено для ограничения изобретения показанными и описанными конкретными вариантами реализации. Далее в целях понимания элементы вариантов реализации описаны во время работы. Однако очевидно, что соответствующие элементы выполнены с возможностью осуществления функций, описываемых как выполняемые ими. Кроме того, настоящее изобретение не ограничивается этими вариантами реализации, и изобретение заключается в каждом из новых признаков или комбинации признаков, описанных в данном документе или изложенных во взаимно отличающихся зависимых пунктах формулы изобретения.
Напомним, что существуют несколько схем, основанных на решетка, для разработки протокола обмена ключами (KEX), механизма инкапсуляции ключей (KEM; иногда называемого также методом инкапсуляции ключей), шифрования с открытым ключом (PKE), цифровых подписей и т. д. Примерами этих схем являются:
Frodo, которая представляет собой KEX, основанный на задаче обучения с ошибками (Learning with Errors, LWE);
NewHope, которая представляет собой KEX, основанный на задаче обучение с ошибками в кольце (Ring Learning with Errors, RLWE);
NewHopeSimple, которая представляет собой KEM, предназначенный для атаки с выбором открытого текста (CPA) на основе RLWE;
Kyber, которая представляет собой CPA-KEM и CCA-KEM на основе задачи модульного LWE.
spKEX, которая представляет собой KEX, основанный на задаче обучения с округлением (Learning with Rounding, LWR).
Каждая из вышеуказанных схем реализует криптографический протокол (например, KEX, KEM, PKE, цифровая подпись), опирающийся на одну основополагающую задачу теории решеток: либо LWE, либо LWR, либо модульное LWE для фиксированного кольца, либо LWR.
NewHope и NewHopeSimple опираются только на RLWE с использованием кольца 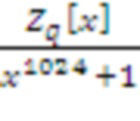
Kyber опирается только на объединение k модулей, причем каждый модуль представляет собой многочлены в 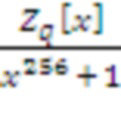
spKEX опирается только на LWR.
Frodo опирается только на LWE.
Хотя все вышеуказанные задачи связаны, некоторые из них считаются более рискованными в том смысле, что они полагаются на конкретные структуры. С другой стороны, использование структуры кольца делает возможными более мелкие сообщения. Хотя в настоящее время об атаках с использованием таких структур неизвестно, такие атаки могут стать известными в будущем. Тогда все схемы, основанные на этих конкретных задачах (например, RLWE или модульное LWE), будут взломаны. Поэтому существует потребность в запасном варианте. Таким образом, необходимо реализовывать и испытывать множество схем, некоторые из которых основаны на более рискованных задачах, но с более хорошими свойствами производительности, а некоторые основаны на хорошо изученных задачах, но с менее хорошей производительностью.
Авторы изобретения поняли, что вышеуказанные задачи теории решеток связаны, и нашли схему, которая может реализовывать все такие задачи, включая: RLWE, RLWR, модульное LWE, модульное LWR, LWE и LWR. Ниже описаны несколько примеров криптографии, в которых разные решетки создаются на основе параметра  сложности и параметра
сложности и параметра  структуры.
структуры.
Изменяя параметры в этой схеме, мы можем, таким образом, реализовывать протоколы (KEX, KEM, PKE и т. д.) на основе разных лежащих в основе задач и проявляющих разные свойства производительности.
Эта схема может быть применена к нескольким областям применения с разными потребностями в безопасности/производительности. Например, совершенно секретные документы могут быть зашифрованы с использованием настроек схемы для LWE, тогда как выработка общего ключа по беспроводной связи с ограниченными ресурсами может быть основана на параметрах LWR в кольце. Схема имеет дополнительные преимущества: во-первых, она уменьшает размер кода, поэтому требуется меньше памяти. Во-вторых, усилия по проверке кода сведены к минимуму, т. к. требуется проверить один алгоритм и подтвердить его правильность. Наконец, такая схема подготавливает к потенциальному сценарию перехода, в котором опора на «более слабую» задачу (например, RLWE) больше ненадежна и требуются новые алгоритмы, опирающиеся на «более стойкую» задачу (например, основанную на LWE). Схема не опирается на две разные спецификации, одну для задачи 1 и другую для задачи 2 и т. д., а использует один и тот же алгоритм для реализации разных задач, причем единственным отличием являются входные параметры.
В основном изобретении использована задача о решетке размера d, где d является входным параметром. Размер решетки может быть размером, соответствующим RLWE, RLWR, модульному LWE, модульному LWR, LWE, LWR. Схема опирается на матрицу, содержащую k × k элементов, где каждый элемент является элементом в Zq[x]/f[x], f[x] - многочлен приведения по модулю степени n, а n - входной параметр. k определено как d/n и не является входным параметром; в вариантах реализации предполагают, что d является кратным n.
Таким образом, если даны фиксированные размер d решетки и степень n многочлена приведения, мы получаем количество элементов (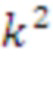 ) матрицы. Обратите внимание, что в этом заключается основное отличие от модульных решеток. Например, в таких решетках некоторые авторы оптимизируют операции кольца в кольце многочленов (а именно,
) матрицы. Обратите внимание, что в этом заключается основное отличие от модульных решеток. Например, в таких решетках некоторые авторы оптимизируют операции кольца в кольце многочленов (а именно, 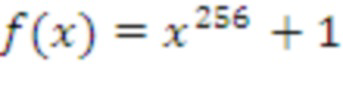 ), и они используют количество модулей для «увеличения» размера решетки следующим образом: d = 256 * k. Эта схема может быть реализована только в виде модульного RLWE или RLWE, которое слишком мало для целей защиты.
), и они используют количество модулей для «увеличения» размера решетки следующим образом: d = 256 * k. Эта схема может быть реализована только в виде модульного RLWE или RLWE, которое слишком мало для целей защиты.
Если n = 1, то это представляет матрицу для LWE или LWR.
Если n = d, то это представляет матрицу для RLWE или RLWR.
Если 1 < n <d, то это представляет матрицу для модульного LWE или модульного LWR.
Без потери обобщенности отметим, что в последующих разделах часто фокусируется внимание только на двух случаях, а именно: n = 1 и n = d.
KEX на основе LWR и NTRU-RING LWR
Далее мы будем использовать кольцо NTRU для иллюстрации наших вариантов реализации. На практике также могут быть использованы другие кольца, такие как (простые) круговые многочлены при условии, что q является простым элементом, обеспечивающим, что n = 1 (mod p). В альтернативном варианте реализации можно также взять (простые) круговые многочлены с q, являющимся степенью двойки. Дополнительное ограничением состоит в том, что (простой) круговой многочлен неприводим по модулю 2.
Кольцо NTRU представляет собой 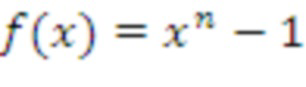 , где
, где  является простым числом. Затем для данной задачи с решеткой размера d можно реализовать систему, например при
является простым числом. Затем для данной задачи с решеткой размера d можно реализовать систему, например при  или
или  . Если
. Если  , получаем NTRU-RING LWR, а если
, получаем NTRU-RING LWR, а если  , получаем схему LWR. Можно также взять входной параметр d > n и d, причем d кратное простому n, так сто получаем модульное LWR с использованием кольца NTRU.
, получаем схему LWR. Можно также взять входной параметр d > n и d, причем d кратное простому n, так сто получаем модульное LWR с использованием кольца NTRU.
Таблица 1. Описание протокола KEX высокого уровня. Обратите внимание, что round(vector, p, q) означает выполнение округления с использованием модулей p и q. Обратите внимание, что игнорированы подробные сведения о том, как выполняют согласование ключа, поскольку они не являются основополагающими для данного описания. Приведенная ниже информация содержит также протоколы PKE, CPA-KEM и CCA-KEM, включая все необходимые подробности.
Создание общей матрицы A с d/n × d/n элементами в Z [x]/f[x]
Создание секрета s, содержащего d/n элементов в Z [x]/f[x]
Создание открытого ключа b = round(A s, p, q) с d/n элементами в Zp[x]/f(x), где A s является произведением матрицы A и вектора s секрета, вычисленным по модулю f(x) и модулю q
Отправка (b, A)
Создание матрицы открытого ключа u = round(r^t A, p, q) с d/n элементами в Zp[x]/f(x), где r^t A является матричным произведением транспонированного вектора r секрета и общей матрицы A, вычисленным по модулю f(x) и модулю q
Вычисление необработанного ключа rkr=(r^t b) (mod p), содержащего d/n элементов в Zp[x]/f(x), где r^t b является матричным произведением транспонированного вектора r секрета и матрицы b, вычисленным по модулю f(x) и модулю p
Вычисление данных согласования (h) из rkr
Отправка (u, h)
Вычисление итогового ключа из h и rki
Из приведенного выше можно увидеть, что в зависимости от выбора n лежащей в основе задачей является RLWR (если n = d) или LWR (n = 1). В обоих случаях лежащая в основе задача теории решеток имеет размер d. Следует отметить, что уровень техники будет иметь две различные реализации вышеуказанного алгоритма, а именно:
Таблица 2. Обратите внимание, что мы игнорировали округление, требуемое в LWR при вычислении открытых ключей b и u, т. к. это не существенно для описания. Мы также игнорируем подробности, касающиеся того, каким образом может быть выполнено согласование ключей, см. ссылки.
Обратите внимание, что rki и rkr являются необработанными ключами инициатора и ответчика, соответственно.
Как описано в уровне техники и формулировке проблемы, нынешние схемы, приведенные в таблице 2, опираются на одну задачу и, следовательно, оптимизированы с помощью слегка отличающихся параметров и алгоритмов. Например, задачи RLWE обычно опираются на кольцо Zq[x]/x^n + 1, где n является степенью двойки, а q является простым числом, поэтому можно использовать теоретико-числовое преобразование (Number Theoretic Transform, NTT). Эти варианты не являются оптимальными для объединения с версиями без кольца, т. к. для этого требуется, чтобы q было простым, что делает модульные операции более сложными при выполнении матричных операций.
Схема в таблице 1 определена для работы с аналогичными параметрами и процедурами. В частности, по этой причине в данном описании используется кольцо NTRU, поскольку оно опирается на q, которое представляет собой степень двойки, что также является хорошим выбором для схем LWE/LWR. Этот также позволяет нам использовать ту же процедуру для этапа согласования ключа, которая опирается на тот факт, что и p, и q являются степенями двойки [2]. Эти тонкости подробно объяснены в последующей информации ниже, поясняющей вариант реализации для CPA-PKE, CPA-KEM и CCA-KEM.
В некоторых вариантах реализации первый этап инициатора в криптографическом протоколе, обобщенном в таблице 1, может содержать PST.CPA-KEM.Keygeneration или PST.NR.CCA-KEM.Keygen, как подробно описано ниже, или любой их вариант, например, операцию формирования ключа механизма инкапсуляции ключей. Аналогичным образом этап ответчика может содержать PST.CPA-KEM.Encapsulate или PST.NR.CCA-KEM.Encapsulate, как подробно описано ниже, или любой их вариант, например, операцию инкапсуляции ключа механизма инкапсуляции ключей. Второй этап инициатора может содержать PST.NR.CPA-KEM.Decapsulate, PST.NR.CCA-KEM.Decapsulate, как подробно описано ниже, или любой их вариант, например, операцию декапсуляции ключа механизма инкапсуляции ключей (KEM). В данном случае криптографическая операция может быть обменом ключом или инкапсуляцией ключа.
В других вариантах реализации первый этап инициатора в криптографическом протоколе, обобщенном в таблице 1, может включать PST.NR.CPA-PKE.Keygeneration(), как подробно описано ниже, или любой ее вариант, например, операцию формирования ключа схемы шифрования открытого ключа. Этап ответчика может содержать PST.NR.CPA-PKE.Encryptwithrho() или PST.NR.CPA-PKE.Encrypt(), как подробно описано ниже, или любой их вариант, например, операцию шифрования схемы шифрования открытого ключа. Второй этап инициатора может содержать PST.NR.CPA-PKE.Decrypt(), как подробно описано ниже, например, операцию расшифрования схемы шифрования открытого ключа. В этом случае криптографическая операция может быть шифрованием открытого ключа. При шифровании открытого ключа этап ответчика и второй этап инициатора могут быть повторены, например, для шифрования и дешифрования сообщений, и, в частности, второй этап инициатора может быть исполнен несколько раз на множестве устройств, чтобы устройство могло выполнять второй этап инициатора без выполнения перед этим первого этапа инициатора.
Дальнейшие варианты реализации подробно описаны ниже со ссылкой на Фиг. 1.
Обратите внимание, что в протоколе, приведенном в качестве примера в таблице 1, имеются ссылки на round (), которая является функцией, выполняющей округление, как определено в задаче LWR. В частности, округление может включать этапы умножения немасштабированного элемента на p и деление на q, округления до целого числа (например, ближайшего целого числа), и взятия округленного элемента по модулю p, что эффективно добавляет шум к записи.
Базовая реализация (часть 1)
Базовая реализация схемы, приведенной в таблице 1, будет включать следующие процедуры для получения элементов открытого ключа (b и u) и необработанных ключей (rki и rkr):
Вычисление открытых ключей:
Result[] = Computation of public-key(A[,],s[])
Result[] = 0
For (i=0 to d/n)
For (j=0 to d/n)
Result[i] = Add_elements(Result[i], Multiply_elements[A[i,j],s[j])
C[]=Add_elements(A[],B[])
For(i=0 to n)
C[i]=(A[i]+B[i] (mod q))
C[]=Multiply_elements(A[],B[])
C[] =0
For(i=0 to n)
For (j=0 to n)
C[i]=C[i]+ A((i-j)mod n)*B[j] mod q
Обратите внимание, что в вышеприведенных процедурах не включен этап округления с использованием модулей p и q, как в таблице 1. Однако это не существенно для данного изобретения. Если бы осуществлялась версия LWE данной схемы, округление было бы заменено добавлением шума (например, гауссовского шума с математическим ожиданием 0 и малым стандартным отклонением) в Z_q[x]/f(x).
Вычисление необработанных ключей:
Result[] = Computation of raw-key(b[],s[])
Result[] = 0
For (i=0 to d/n)
Result[i] = Add_elements(Result[i], Multiply_elements[b[i],s[i])
C[]=Add_elements(A[],B[])
For(i=0 to n)
C[i]=(A[i]+B[i] (mod p) (mod x^n - 1)
C[]=Multiply_elements(A[],B[])
For(i=0 to n)
C[i]=(A[(n-i)mod(n)]+B[i]) (mod p) (mod x^n - 1)
Обратите внимание, что в алгоритмах для вычисления необработанных ключей мы пишем mod p, т. к. рассматривается обучение с округлением. В случае версии обучения с ошибками (в кольце) настоящего изобретения мы добавляли бы шум вместо выполнения округления, и вычисления были по модулю q.
Базовая реализация (часть 2)
Следует отметить, что секреты, связанные с инициатором и ответчиком в протоколе (KEX, KEM, PKE и т. д.), могут представлять собой больше одного вектора, содержащего d/n элементов в Zq[x]/f(x), но могут содержать n_bar и m_bar этих векторов. Например, секрет s может быть закрытой матрицей, например, матрицей закрытого ключа, открытый ключ b может быть открытой матрицей, например, матрицей открытого ключа, секрет r может быть закрытой матрицей, например, матрицей закрытого ключа, и открытый ключ u может быть открытой матрицей, например матрицей открытого ключа. Для формирования достаточного количества битов ключа предпочтительно, чтобы n_bar и m_bar были больше единицы. Таким образом, все операции в схеме в базовой реализации могут быть представлены как произведения двух матриц, элементы которых находятся в Zq[x]/f(x). В частности, для вычисления b можно вычислить матричное произведение A и s, для вычисления u можно вычислить матричное произведение A и r и для вычисления rkr можно вычислить матричное произведение b и r или b и s.
Для этого требуется следующая родовая функция:
C = Multiply (A, B, A_c, A_r, B_c, B_r, n)
где A и B представляют собой входные матрицы размеров (A_c × A_r) и (B_c × B_r), соответственно. Каждый элемент в матрице содержит элемент в Zq[x]/f(x), который может быть представлен как n элементов в Zq. Выходная матрица C имеет размер (C_c × C_r) = (A_r × B_c).
Далее, в некоторых случаях требуется функция для транспонирования матриц. Для этого требуется функция:
B = Transpose (A, A_c, A_r, n)
где A - входная матрица размера (A_c × A_r). Каждый элемент в матрице содержит элемент в Zq[x]/f(x), который может быть представлен как элементы в Zq. Выходная матрица B имеет размер (B_c × B_r) = (A_c × A_r).
Конкретный способ кодирования информации в матрице заключается в использовании вектора, который хранит элементы самого низкого уровня в Zq. Например, если q = 214, то для хранения каждого элемента могут быть использованы два байта. Матрица A размера (A_c × A_r) с элементами в Zq[x]/f(x) может храниться в векторе длиной A_r * A_c * n * 2 байтов (в предположении, что q <= 216). Этот вектор будет кодировать A: (i) строку за строкой, (ii) в каждой строке столбец за столбцом, и (iii) затем n элементов в Zq.
Вышеуказанные две функции (Multiply() и Transpose()) будут осуществлять доступ к вектору, используемому для хранения матриц подходящим образом. Этим также объясняется, почему n передают в качестве входного параметра этим двум функциям.
Оптимизированная реализация вычисления открытого ключа (часть 1)
Для фиксированного параметра d безопасности вышеуказанная базовая реализация является быстрой в случае 
 , т. к. матрица A содержит один элемент, который представляет собой многочлен из
, т. к. матрица A содержит один элемент, который представляет собой многочлен из 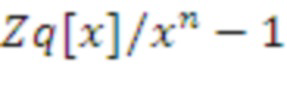
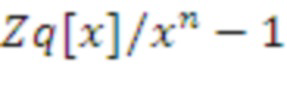 в предположении, что n_bar = m_bar = 1. Для
в предположении, что n_bar = m_bar = 1. Для 
 базовая реализация будет медленной, т. к. A содержит
базовая реализация будет медленной, т. к. A содержит 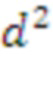
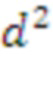 элементов, причем каждый элемент является элементом в Zq, а скалярное произведение реализуют как обычное умножение многочленов.
элементов, причем каждый элемент является элементом в Zq, а скалярное произведение реализуют как обычное умножение многочленов.
Для оптимизированной реализации можно использовать тот факт, что в случае 
 операции умножения многочленов могут быть выражены как умножение матрицы размера d × d = n × n над Zq и вектора длины d с элементами в Zq :
операции умножения многочленов могут быть выражены как умножение матрицы размера d × d = n × n над Zq и вектора длины d с элементами в Zq :
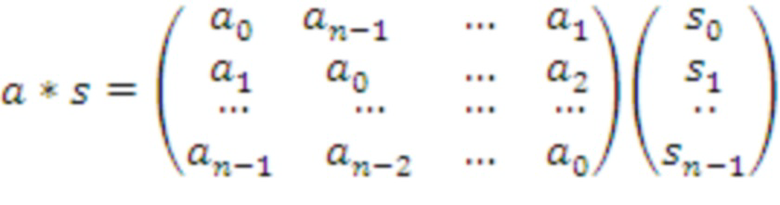
Используя этот факт при реализации вычисления открытого ключа можно всегда предполагать, что входная матрица A, например, представленная в виде расширенной общей матрицы, будет содержать 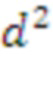
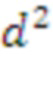 различных элементов для
различных элементов для 
 (LWR) и d различных элементов для
(LWR) и d различных элементов для 
 (RLWR). Другими словами, расширенная матрица может иметь количество столбцов и строк, равное параметру d сложности, и может быть вычислена путем замены элементов-многочленов вышеуказанной циркулянтной матрицей. Единственная разницам между алгоритмами при выполнении умножений матриц состоит в том, что умножение матриц для ответчика выполняют слева для
(RLWR). Другими словами, расширенная матрица может иметь количество столбцов и строк, равное параметру d сложности, и может быть вычислена путем замены элементов-многочленов вышеуказанной циркулянтной матрицей. Единственная разницам между алгоритмами при выполнении умножений матриц состоит в том, что умножение матриц для ответчика выполняют слева для 
 и справа для
и справа для 
 . Другими словами, общая часть, относящаяся к умножению матриц, часть может быть использована для разных значений параметра структуры и/или параметра сложности.
. Другими словами, общая часть, относящаяся к умножению матриц, часть может быть использована для разных значений параметра структуры и/или параметра сложности.
В альтернативном варианте реализации коэффициенты многочленов могут быть организованы в виде векторов строк, и мы используем, что
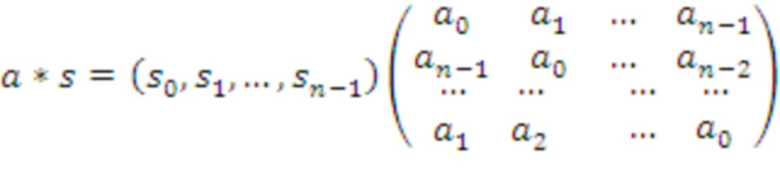
Оптимизированная реализация вычисления открытого ключа (часть 2)
Как раскрыто в соответствующей заявке Philips [1], A может быть эффективно обновлена при наличии эталонной матрицы A_master путем применения перестановки. Перестановка может быть, например, циклическим сдвигом (на выбранное случайным образом смещение (от 0 до n - 1) n' строк (0 <= n' < n) в A_master.
Это можно расширить естественным образом, рассматривая A_master как вектор a_master длины L и применяя к нему перестановку для получения строк A. Мы различаем три случая с весьма конкретными перестановками:
Случай 1: 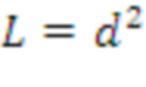
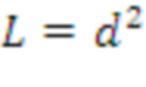 и перестановка для получения строки
и перестановка для получения строки 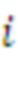
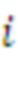 матрицы
матрицы 
 представляет собой взятие d последовательных элементов, начиная с позиции
представляет собой взятие d последовательных элементов, начиная с позиции 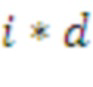
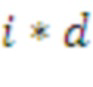 вектора
вектора 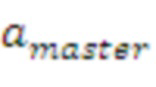
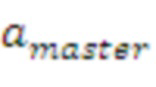 , и циклическое перемещение их по кругу на выбранное случайным образом смещение от 0 до d - 1.
, и циклическое перемещение их по кругу на выбранное случайным образом смещение от 0 до d - 1.
Случай 2: 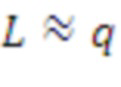
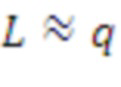 и перестановка для получения строки
и перестановка для получения строки 
 матрицы
матрицы 
 представляет собой взятие
представляет собой взятие 
 последовательных элементов, начиная с элемента
последовательных элементов, начиная с элемента 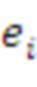
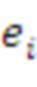 вектора
вектора 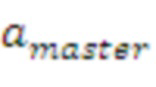
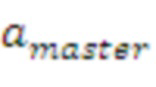 , где
, где 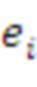
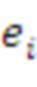 - выбранное случайным образом значение в
- выбранное случайным образом значение в 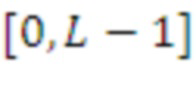
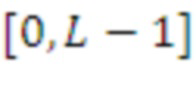 , и заканчивая элементом
, и заканчивая элементом 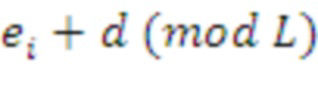
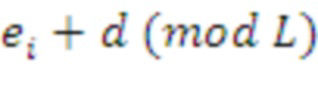 (таким образом, учитывая также циклическую структуру).
(таким образом, учитывая также циклическую структуру).
Случай 3: 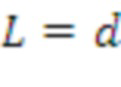
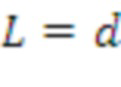 и перестановка для получения строки
и перестановка для получения строки 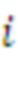
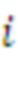 матрицы
матрицы 
 представляет собой взятие
представляет собой взятие 
 последовательных элементов (учитывая также циклическую структуру), начиная с элемента
последовательных элементов (учитывая также циклическую структуру), начиная с элемента 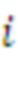
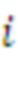 вектора
вектора 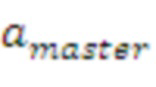
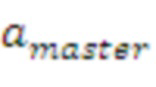 .
.
Очевидно, вышеприведенные три случая могут быть дополнительно обобщены путем использования других типов перестановок или создания 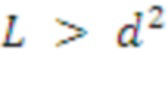
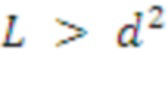 . Что касается трех случаев в данном подходе:
. Что касается трех случаев в данном подходе:
Случай 1 реализует схему, описанную в настоящем документе для 
 . Если
. Если 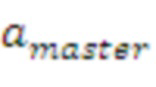
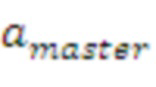 вычисляют случайным образом, то получающаяся в результате
вычисляют случайным образом, то получающаяся в результате 
 невозможно отличить от случайной матрицы. Поскольку элементы перемещаются по кругу на выбранное случайным образом смещение, то при наличии фиксированного a_master этот подход позволяет эффективно получать свежую A.
невозможно отличить от случайной матрицы. Поскольку элементы перемещаются по кругу на выбранное случайным образом смещение, то при наличии фиксированного a_master этот подход позволяет эффективно получать свежую A.
Случай 3 реализует схему для 
 и обеспечивает эффективный способ получения матричного представления
и обеспечивает эффективный способ получения матричного представления 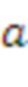
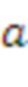 в полиномиальной свертке
в полиномиальной свертке 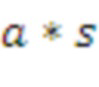
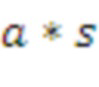 .
.
Случай 2 промежуточный между структурой с кольцом и структурой без кольца. В данном случае невозможно приведение к (LWR) ввиду наличия некоторого перекрытия между строками в A, т. к. L < d2. Таким образом, можно отличать получающуюся в итоге матрицу 
 от случайной матрицы. Однако с практической точки зрения данный подход разрушает однокольцевую структуру в получающейся в результате
от случайной матрицы. Однако с практической точки зрения данный подход разрушает однокольцевую структуру в получающейся в результате 
 , т. к. она содержит гораздо больше элементов. По существу в каждой строке используют отличное от других кольцо.
, т. к. она содержит гораздо больше элементов. По существу в каждой строке используют отличное от других кольцо.
В случае внедрения вышеуказанного подхода к оптимизированной реализации (часть 1) можно реализовать матричное умножение посредством 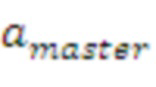
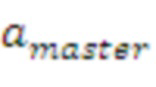 данной длины
данной длины 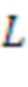
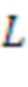 , перестановки некоторых конкретных компонентов и секрета
, перестановки некоторых конкретных компонентов и секрета 
 . В зависимости от выбора длины
. В зависимости от выбора длины 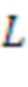
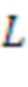 и перестановки один и тот же алгоритм эффективно реализует матричное умножение, как для
и перестановки один и тот же алгоритм эффективно реализует матричное умножение, как для 
 , так и для
, так и для 
 .
.
Следует отметить, что в случае 1 вектор a_master может быть использован повторно, причем его и свежие матрицы A получают путем изменения перестановок строк. В случае 3 рекомендуется регулярно обновлять a_master.
Это обобщено в следующей таблице, из которой видно, что в зависимости от выбора L можно получать разные производительности и обеспечения безопасности. Как можно увидеть, взятие L = q не дает выгод с точки зрения пропускной способности, т. к. структура разрушается, и для передачи A требуется передавать больше информации; однако с точки зрения ЦП данный подход более эффективен, т. к. требуется вычисление меньшего количества случайных чисел.
Оптимизированная реализация (часть 3)
Та же идея с перестановкой может быть применена к вычислению необработанного ключа, учитывая, что в обоих случаях открытый ключ содержит d элементов в Zp. Для 
 они действительно являются
они действительно являются 
 элементами в
элементами в 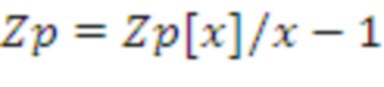
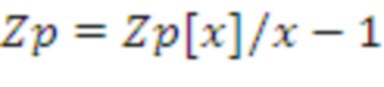 . Для
. Для 
 эти
эти 
 элементов являются коэффициентами многочлена в
элементов являются коэффициентами многочлена в 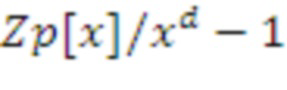
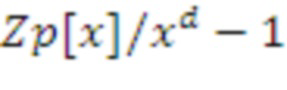 .
.
Для 


 элементов принятого открытого ключа обрабатывают в порядке приема, но в случае
элементов принятого открытого ключа обрабатывают в порядке приема, но в случае 


 элементов сначала нужно переупорядочить, чтобы восстановить порядок первой строки матрицы, которая будет реализовывать оценку многочлена. После этого можно определить два преобразования:
элементов сначала нужно переупорядочить, чтобы восстановить порядок первой строки матрицы, которая будет реализовывать оценку многочлена. После этого можно определить два преобразования:
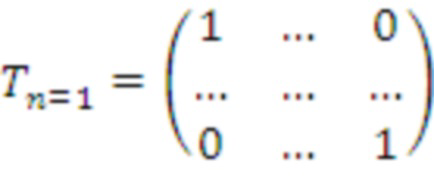
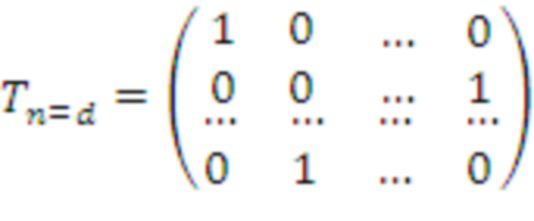
Кроме того, предполагается применение двух перестановок для получения матрицы, напоминающей умножение многочленов
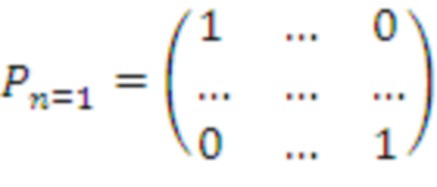
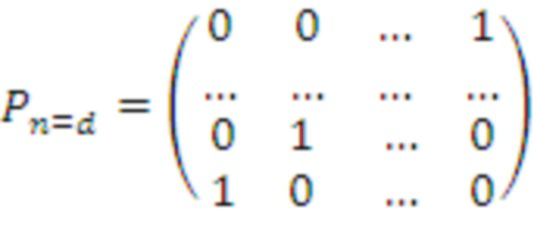
С учетом этого оптимизированный алгоритм для получения необработанного ключа работает следующим образом:
Result[] = Computation of raw-key(b[],s[])
Result[] = 0
For (i=0 to n)
For j=0 to d
Result[i] = 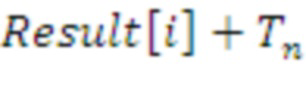
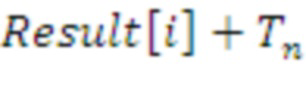 (b)[(
(b)[(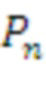
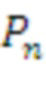 (j) + i) mod(d)] * s(j)
(j) + i) mod(d)] * s(j)
Обратите внимание, что преобразование 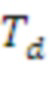
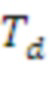 необходимо, поскольку принимается вектор коэффициентов
необходимо, поскольку принимается вектор коэффициентов 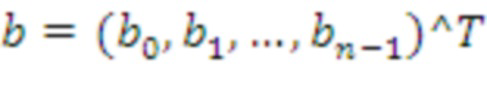
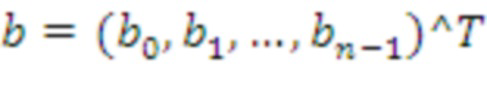 и нужно получить верхнюю строку циркулянтной матрицы с b в качестве крайнего левого столбца.
и нужно получить верхнюю строку циркулянтной матрицы с b в качестве крайнего левого столбца.
В вышеуказанном алгоритме 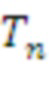
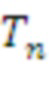 действует на
действует на 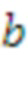
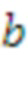 для переупорядочения элементов надлежащим образом, а
для переупорядочения элементов надлежащим образом, а 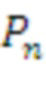
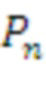 выполняет сдвиг на
выполняет сдвиг на 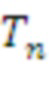
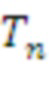 (b) для выполнения операций приведения по модулю.
(b) для выполнения операций приведения по модулю.
Оптимизированная реализация (часть 4)
Ключевым аспектом для оптимизированной реализации является осуществление перестановки на a_master. Для этого требуется реализация приведений по модулю L и модулю d. Это имеет свои недостатки в отношении производительности и атак по побочным каналам. Во избежание этих приведений по модулю, например, на векторе v:
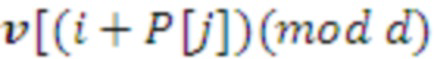
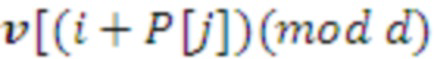 ]
]
оптимизированная реализация может работать с вектором v_star, который просто содержит копию вектора.
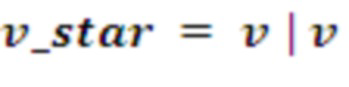
Где | обозначает конкатенацию. Это увеличивает требования к памяти, но исключает приведение по модулю.
Следует также отметить, что данный подход может позволить реализовать другие кольца эффективным образом. Например, в случае использования кольца Zq[x]/x^n + 1 вектор v_star можно было бы получить следующим образом:
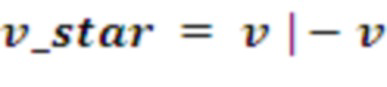
Действительно, тогда бы получилось, что
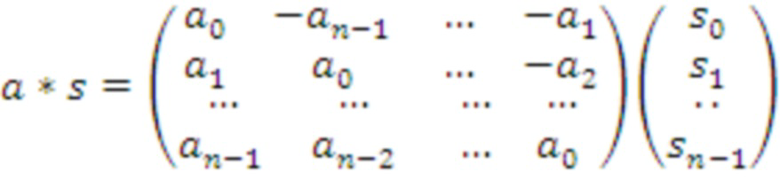
Поэтому A имеет знаки минуса выше диагонали; действительно, A(i,j) =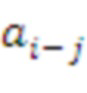
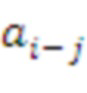 , если
, если 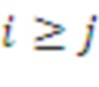
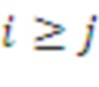 , и
, и 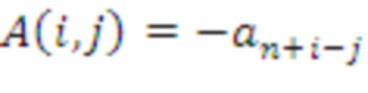
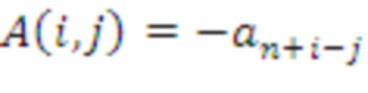 , если
, если 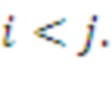
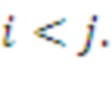 Поскольку
Поскольку 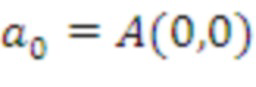
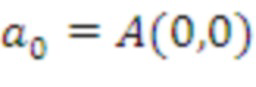 и
и 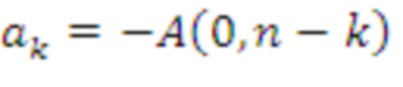
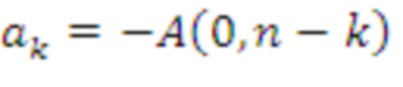 для
для 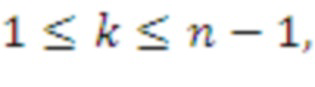
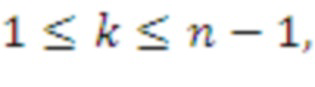 отсюда следует, что
отсюда следует, что 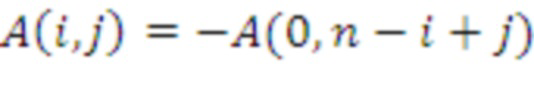
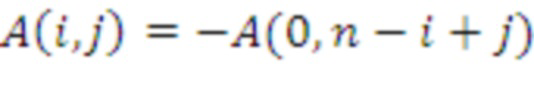 , если
, если 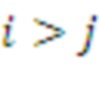
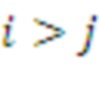 , и
, и 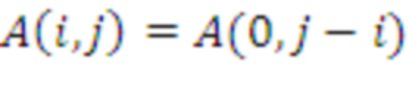
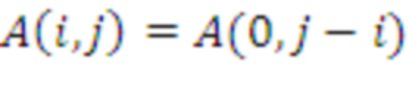 , если
, если 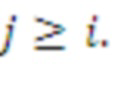
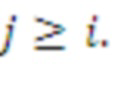 Поэтому
Поэтому 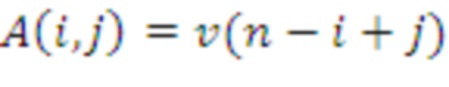
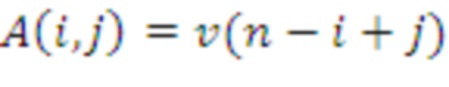 , где
, где 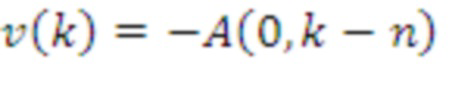
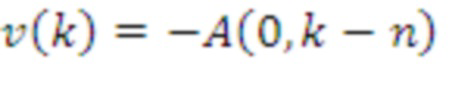 , если
, если 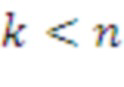
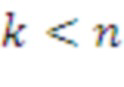 , и
, и 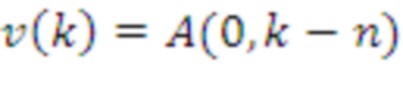
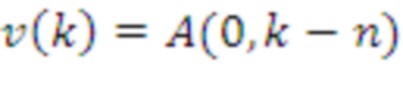 для
для 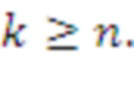
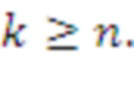
CPA-PKE, CPA-KEM и CCA-KEM на основе LWR и NTRU-RING LWR
Дальнейшая информация, приведенная ниже, описывает порядок построения протоколов CPA-PKE, CPA-KEM и CCA-KEM на основе уже описанных идей. Таким образом, эти протоколы могут быть созданы на основе LWR или NTRU-RING LWR всего лишь путем использования разных параметров конфигурации.
Кольцо NTRU имеет многочлен приведения по модулю 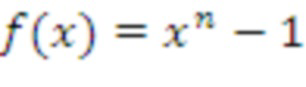
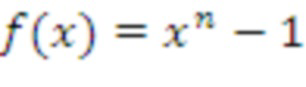 , где
, где 
 представляет собой простое число. Тогда для задачи с решеткой данного размера d можно реализовать систему с
представляет собой простое число. Тогда для задачи с решеткой данного размера d можно реализовать систему с 
 или
или 
 . Если
. Если 
 , получаем NTRU-RING LWR, а если
, получаем NTRU-RING LWR, а если 
 , получаем схему LWR.
, получаем схему LWR.
Следует отметить, что даже при использовании в описании в качестве входных параметров (d, n) либо (d,d), либо (d,1) также можно получить даже еще более общую конфигурацию, в которой входными параметрами являются (k * n, n), где n может быть либо 1, либо простым числом (в случае кольца NTRU).
Другие варианты реализации:
Следует отметить, что описание не опирается на тип секрета или на факт использования округления или стандартного добавления шума (либо гауссовского, однородного, либо любого другого распределения). Таким образом, настоящее изобретение может быть реализовано для любого типа распределения секрета.
Применимость к RLWE: В дальнейшей информации, приведенной ниже, содержатся конкретные варианты выбора для кольца, а p и q являются степенями двойки. Эти варианты продиктованы конкретным типом способа согласования ключа и тем фактом, что использование в качестве p и q степени двойки, приводит к эффективной реализации. В альтернативных вариантах реализации изложенные в настоящем документе идеи применяются к R/LWE. В этом случае вместо применения округления нужно добавлять шум.
Применимость к другим протоколам: в настоящем документе показано, как применять наш подход к построению of KEX, KEM или PKE. Та же самая методология работает для схем типа схема Эль-Гамаля. Эта схема также может быть применима к другим схемам, таким как подписи.
Использование других колец
Большинство вариантов реализации в настоящем документе основаны на многочлене кольца NTRU 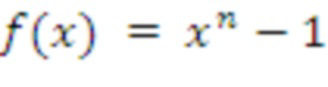
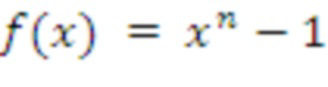 . Однако этом многочлен не является неприводимым и равен (x - 1)(x^(n - 1) + x^(n - 2) +…+ x + 1. Благодаря этому найти решение задачи RLWE (b = as + e) не составляет труда. Тем не менее, нахождение s остается сложным.
. Однако этом многочлен не является неприводимым и равен (x - 1)(x^(n - 1) + x^(n - 2) +…+ x + 1. Благодаря этому найти решение задачи RLWE (b = as + e) не составляет труда. Тем не менее, нахождение s остается сложным.
В литературе используются другие кольца, которые могут быть применены в вышеприведенных вариантах реализации. Например, можно использовать циклотомические кольца в виде 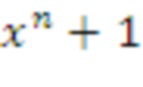
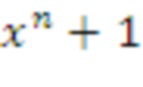 , где n является степенью двойки, а q является простым числом и
, где n является степенью двойки, а q является простым числом и 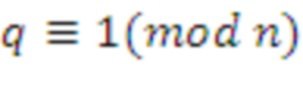
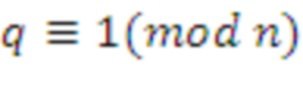 . Также можно использовать простые циклотомические кольца вида
. Также можно использовать простые циклотомические кольца вида 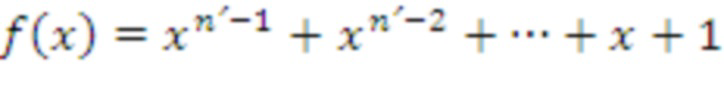
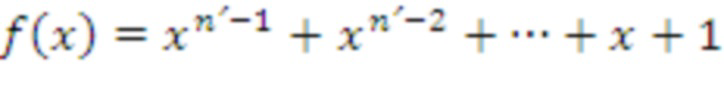 и простое число в качестве q, причем
и простое число в качестве q, причем 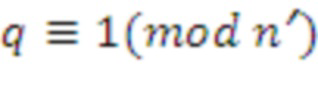
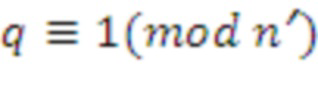 . В этом случае параметр n структуры может быть на единицу меньше простого числа
. В этом случае параметр n структуры может быть на единицу меньше простого числа 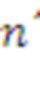
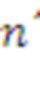 , определяющего простое циклотомическое кольцо, так что в криптографической операции могут быть использованы целочисленные многочлены степени меньше параметра структуры.
, определяющего простое циклотомическое кольцо, так что в криптографической операции могут быть использованы целочисленные многочлены степени меньше параметра структуры.
Эти кольца могут быть использованы способом, аналогичным показанному выше для кольца NTRU. Например, тогда случай без кольца (LWE) реализуют с помощью кольца 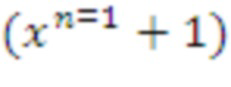
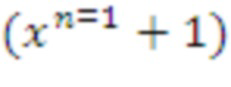 или (1), когда
или (1), когда 
 приведенных выше циклотомических колец. Обратите внимание, что в обоих случаях q является простым числом. Следует отметить, что способ согласования ключа отличается от используемого в варианте реализации, подробно описанном выше, т. к. требуется, чтобы q было степенью двойки. Подходящим вариантом будет согласование ключа как в Frodo.
приведенных выше циклотомических колец. Обратите внимание, что в обоих случаях q является простым числом. Следует отметить, что способ согласования ключа отличается от используемого в варианте реализации, подробно описанном выше, т. к. требуется, чтобы q было степенью двойки. Подходящим вариантом будет согласование ключа как в Frodo.
Другим хорошим вариантом является использование циклотомических многочленов, как показано выше, а именно, 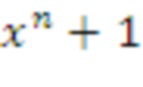
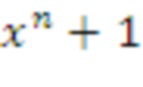 и
и 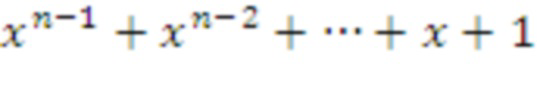
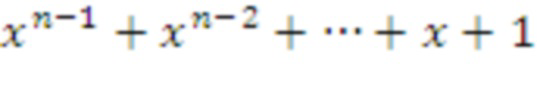 , и использовать q, которое является степенью двойки, а не простым числом. Требование, чтобы q было простым, в основном предназначено для использования NTT, однако для реализации нашей схемы q лучше выбирать равным степени двойки, т. к. реализация схемы посредством умножений матриц является хорошим вариантом.
, и использовать q, которое является степенью двойки, а не простым числом. Требование, чтобы q было простым, в основном предназначено для использования NTT, однако для реализации нашей схемы q лучше выбирать равным степени двойки, т. к. реализация схемы посредством умножений матриц является хорошим вариантом.
Еще один хороший вариант - использование циклотомических многочленов, как указано выше, а именно, 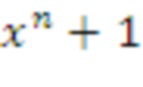
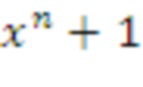 и
и 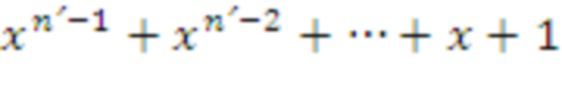
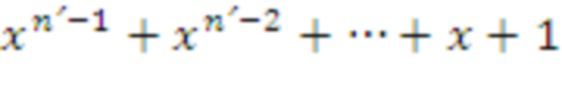 , и использовать q, которое является степенью двойки, при дополнительном требовании, что многочлен неприводим по модулю 2, а параметр n структуры может быть на единицу меньше простого
, и использовать q, которое является степенью двойки, при дополнительном требовании, что многочлен неприводим по модулю 2, а параметр n структуры может быть на единицу меньше простого 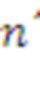
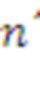 , так что в криптографической операции могут быть использованы целочисленные многочлены, степень которых меньше параметра структуры.
, так что в криптографической операции могут быть использованы целочисленные многочлены, степень которых меньше параметра структуры.
Следует также отметить, что в случае использования простого циклотомического многочлена, 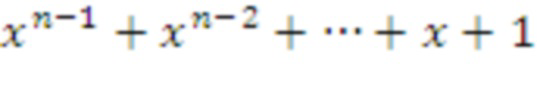
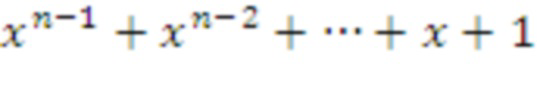 , операции по-прежнему могут выполняться в кольце x^n - 1, поскольку оба кольца отличаются только членом x - 1. Для этого требуется только поднять значения из одного кольца в другое путем умножения на x - 1. После реализации операций можно вернуться в предыдущее кольцо путем деления на ту же величину.
, операции по-прежнему могут выполняться в кольце x^n - 1, поскольку оба кольца отличаются только членом x - 1. Для этого требуется только поднять значения из одного кольца в другое путем умножения на x - 1. После реализации операций можно вернуться в предыдущее кольцо путем деления на ту же величину.
Обоснование выбора параметров с точки зрения производительности
Некоторые оптимизации вычислений, известные для RLWE, не могут быть применены к некоторым вариантам реализации, представленным в настоящем документе. В частности, невозможно применить NTT к кольцу NTRU. В качестве альтернативы можно было бы использовать удобные для NTT параметры, такие как n, равное степени 2, и простые числа q, чтобы операции в Zq[x]/f(x), где f(x) = x^n + 1, могли бы быть выполнены посредством NTT. Данная оптимизация ускорит работу ЦП для случая с кольцом (n > 1) за счет использования NTT, но предполагает более плохую производительность в случае без кольца (n = 1), т. к. операции будут по модулю q (q является простым числом).
Варианты параметров, представленные в настоящем документе, как представляется, являются лучшими для комбинированной схемы, т. к. позволяют быстро реализовывать операции при выполнении их посредством матричных/векторных операций, применимых к любому варианту n. Другими словами, даже если схема для n > 1 может быть не столь эффективной, какой могла бы быть другая схема с кольцом, использующая NTT, вариант в настоящем документе позволят очень быстро реализовывать схему не только при n > 1, но и при n = 1. Кроме того, использование колец NTRU позволяет тонко настраивать требования к безопасности и пропускной способности ввиду наличия множества подходящих колец.
Параметры
Схема может быть сконфигурирована с разными параметрами. Значения d, q и p определяют сложность лежащей в основе задачи теории решеток. Например, типичными значениями являются d около 700, q и p, равные 2^14 и 2^11. В этом случае n_bar и m_bar могут быть равны 8, так что при n = 1 из каждого коэффициента для итоговой матрицы ключа в KEX могут быть получены 4 бита. Когда n= d, на каждый коэффициент многочлена требуется один бит, так что q можно сделать меньше, а значит и p, и, следовательно, n тоже. Так как многочлен имеет n коэффициентов, получают ключ из n битов, а n_bar и m_bar должны быть равны лишь единице.
Следует отметить, что для некоторых вариантов колец может быть несколько наборов параметров. Например, в случае простых циклотомических многочленов могут быть следующие классы параметров:
- Параметры для n = 1 и n = d, определяющие, опирается ли лежащая в основе задача на структуру кольца или нет.
- q, представляющее собой простое или равное степени двойки число, определяющее тип оптимизаций, которые могут быть осуществлены с точки зрения ЦП.
Возможность изменения конфигурации схемы
Схема может быть сконфигурирована для разных уровней защиты и лежащих в основе трудно решаемых задач следующим образом:
Во-первых, для каждой лежащей в основе задачи (например, LWR или RLWR) программа вычисляет целевые параметры (а именно: d, n, q и p) для достижения данного уровня защиты и производительности с точки зрения вероятности отказа, пропускной способности и ЦП. Эта задача может быть выполнена один раз, и затем параметры могут быть опубликованы.
Во-вторых, наборы опубликованных параметров сохраняют в таблице вместе с программой, реализующей схему, предложенную в настоящем документе, причем каждый набор параметров соответствует данной лежащей в основе задаче, уровню защиты и параметрам производительности.
В-третьих, когда две стороны (например, Алиса и Боб) желают пообщаться друг с другом, Алиса информирует Боба о наборе параметров, которые она хочет использовать. Это означает, что Алиса может определять, желает ли она использовать схему, например, в режиме с кольцом или без кольца (варианты d и n), и на каком уровне защиты (зависящем от d, q и p). Алиса может информировать Боба о своем выборе посредством явного задания набора параметров (d, n, q, p, …) путем отправки идентификатора набора параметров или путем задания значений производительности (например, размера открытого ключа, размера закрытого ключа…), которые зависят от выбранных параметров. Следует отметить, что в таком случае у Боба тоже могут быть правила, которые требуют не только минимального уровня защиты, но и определенной трудно решаемой задачи. Таким образом, если предложение от Алисы не устраивает, Боб может запросить другой набор параметров.
Ниже приведены дальнейшая информация относительно вышесказанного и следующие варианты реализации с математической точки зрения в большей мере.
1 Технические характеристики алгоритма и сопроводительная документация
1.1 Обоснование проектных решений
1.2 Основополагающие задачи
1.3 Предварительные сведения
1.4 Шифрование открытого ключа CPA
1.5 Механизм инкапсуляции ключа CPA для случая без кольца
1.6 Платформа механизма инкапсуляции ключа CPA для случая без кольца
1.7 Объединенный случай без кольца и с кольцом
1.7.1 Конфигурации платформы
1.7.2 Наборы параметров
1.7.3 Уровни NIST
1 Технические характеристики алгоритма и сопроводительная документация
1.1 Обоснование проектных решений
Некоторые варианты реализации относятся к платформе алгоритмов для обеспечения инкапсуляции ключей. Предложенные алгоритмы попадают в категорию криптографии на основе теории решеток, в частности, они могут опираться на задачу обучения с округлением (LWR). Эта задача была выбрана для разработки алгоритмов благодаря ее широкому изучению и ее выгодным свойствам в отношении производительности, например пониженных требований к пропускной способности.
Интересным признаком некоторых вариантов реализации является то, что была разработана платформа для «бесшовной» реализации задачи LWR и LWR (RLWR) с кольцом. Это означает, что одни и те же алгоритмы (и код) могут быть использованы для эффективной реализации алгоритмов на основе LWR или RLWR. Основания для такого выбора самые разные.
• Во-первых, это позволяет приспосабливаться к нескольким средам простым способом: с одной стороны, алгоритмы на основе LWR могут быть применены к средам, в которых производительность не так важна, а приоритет отдается безопасности, так что предпочтительно не иметь дополнительной структуры с кольцом. С другой стороны, алгоритмы на основе RLWR достигают наилучшей производительности с точки зрения пропускной способности и вычисления, так что они лучше вписываются в более ограниченные среды.
• Во-вторых, этот подход позволяет использовать стратегию миграции от схем с кольцом к схемам без кольца с самого начала. Это гарантирует, что в случае обнаружения в будущем атак на схемы с кольцом за счет лежащей в основе структуры с кольцом, альтернативное надежное защищенное решение уже доступно и развернуто.
• В-третьих, предложенная платформа сокращает эксплуатационное сопровождение и анализ кода, т. к. одна и та же реализация обеспечивает случаи RLWR и LWR для всех алгоритмов CPA-KEM, CCA-KEM и CCA-PKE.
Вариант реализации дополнительно оптимизирует производительность благодаря нескольким отличительным признакам. Прежде всего, использование LWR и RLWR оптимизирует пропускную способность и избавляет от процедур дискретизации. Во-вторых, выбирают разреженные троичные секреты, поскольку они облегчают реализацию, позволяют повысить производительность и уменьшают вероятность сбоев. В-третьих, для предотвращения атак предварительным вычислением открытую матрицу A не поддерживают постоянной, а обновляют очень эффективным способом для сведения к минимуму ухудшения производительности из-за ее пересчета во время подтверждения установления связи. В-четвертых, функциональные возможности для выполнения округления, сжатия сообщений и расшифрования, реализуют посредством одной и той же функции. Это упрощает и оптимизирует проектное решение. В-пятых, версия с кольцом данного проекта опирается на кольцо NTRU ввиду его хороших характеристик производительности.
1.3 Предварительные сведения
Обозначим кольцо многочленов 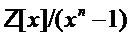 как
как 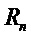 . Здесь n - параметр структуры, а
. Здесь n - параметр структуры, а 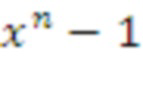
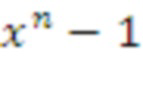 - многочлен приведения по модулю, степень которого равна параметру структуры, так что могут быть использованы многочлены, степень которых меньше структурного параметра. Пусть
- многочлен приведения по модулю, степень которого равна параметру структуры, так что могут быть использованы многочлены, степень которых меньше структурного параметра. Пусть 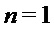 ; тогда
; тогда 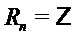 . Допуская некоторую вольность в обозначениях, для каждого положительного целого числа
. Допуская некоторую вольность в обозначениях, для каждого положительного целого числа 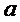 обозначим символом
обозначим символом 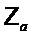 множество
множество 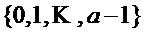 и символом
и символом 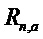 множество многочленов степени меньше
множество многочленов степени меньше 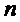 с коэффициентами в
с коэффициентами в 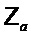 . Многочлен
. Многочлен 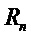 называют троичным, если все его коэффициенты представляют собой 0, 1 или
называют троичным, если все его коэффициенты представляют собой 0, 1 или 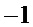 .
.
Везде по тексту настоящего документа буквы обычного шрифта обозначают элементы из 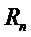 , а выделенные жирным шрифтом строчные буквы представляют векторы с коэффициентами в
, а выделенные жирным шрифтом строчные буквы представляют векторы с коэффициентами в 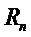 . Все векторы являются векторами столбцов. Выделенные жирным шрифтом заглавные буквы являются матрицами. Транспозицию вектора
. Все векторы являются векторами столбцов. Выделенные жирным шрифтом заглавные буквы являются матрицами. Транспозицию вектора 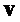 или матрицы
или матрицы 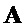 обозначают как
обозначают как 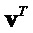 или
или 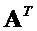 .
.
Приведения по модулю Для положительного целого числа 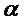 и
и 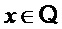 определим
определим 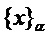 как уникальный элемент
как уникальный элемент 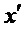 в интервале
в интервале 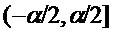 , удовлетворяющий соотношению
, удовлетворяющий соотношению 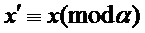 . Кроме того, определим
. Кроме того, определим 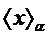 как уникальный элемент
как уникальный элемент 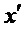 в интервале
в интервале 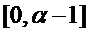 , такой что
, такой что 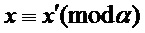 .
.
Округление Для 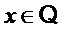 обозначим как
обозначим как 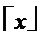 округление
округление 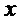 до ближайшего целого числа с округлением вверх, если такие числа с обеих сторон.
до ближайшего целого числа с округлением вверх, если такие числа с обеих сторон.
Сжатие и разуплотнение Пусть 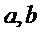 - целые числа, такие что
- целые числа, такие что 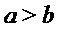 . Определим функции Compress
. Определим функции Compress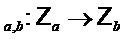 и Decompress
и Decompress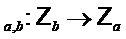 как
как
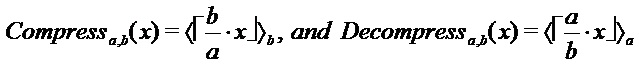
Следовательно, функция Compress может быть использована для добавления шума, например, в элементы матрицы, например, произведения матриц. Например, добавление шума к немасштабированному значению x может включать умножение немасштабированного элемента на модуль b, деление на модуль a, округление до целого числа (например, ближайшего целого числа) и взятие округленного элемента по модулю второго модуля. Можно показать, что функция Decompress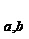 «почти» обратная функции Compress
«почти» обратная функции Compress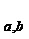 . Точнее говоря, для каждого
. Точнее говоря, для каждого 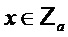

Путем прямого вычисления можно увидеть, что если 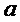 кратно
кратно 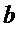 , то
, то
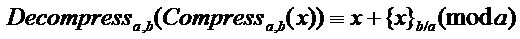
для каждого 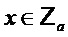 .
.
Функция сжатия служит для трех целей.
• Во-первых, она улучшает безопасность, т. к. она приводит к задаче обучения с округлением.
• Во-вторых, ее используют для расшифрования сообщения.
• В-третьих, она уменьшает размеры открытых ключей и шифртекстов, тем самым снижая требования к пропускной способности.
Для каждого 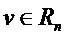 вес Хэмминга
вес Хэмминга 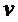 определяют как количество его ненулевых коэффициентов. Вес Хэмминга вектора в
определяют как количество его ненулевых коэффициентов. Вес Хэмминга вектора в 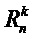 равен сумме весов Хэмминга его компонентов. Обозначим как
равен сумме весов Хэмминга его компонентов. Обозначим как 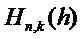 набор всех векторов
набор всех векторов 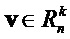 троичных многочленов с весом Хэмминга
троичных многочленов с весом Хэмминга 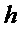 . Если рассматривать коэффициенты многочлена в
. Если рассматривать коэффициенты многочлена в 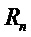 как вектор длины
как вектор длины 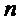 , многочлен в
, многочлен в 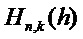 соответствует троичному вектору
соответствует троичному вектору 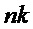 с ненулевыми значениями в
с ненулевыми значениями в 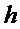 позициях, так что
позициях, так что 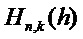 имеет
имеет 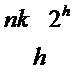 элементов.
элементов.
Для 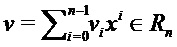 определим
определим 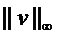 как наибольшее абсолютное значение его коэффициентов, т. е.
как наибольшее абсолютное значение его коэффициентов, т. е.
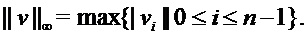
Легко увидеть, что для всех 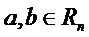 справедливо
справедливо
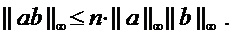
Аналогичным образом, если 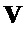 представляет собой матрицу многочленов в
представляет собой матрицу многочленов в 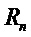 , то
, то 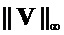 является наибольшим из всех коэффициентов многочленов в
является наибольшим из всех коэффициентов многочленов в 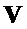 . Наконец, для
. Наконец, для 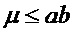 и
и 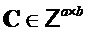 вектор Sample
вектор Sample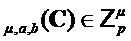 содержит значения в
содержит значения в 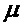 предварительно заданных позициях
предварительно заданных позициях 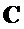 .
.
1.4 Шифрование открытого ключа CPA
В данном разделе описано шифрование открытого ключа для случая без кольца. Наша схема шифрования CPA-стойкого открытого ключа описана с помощью алгоритмов ниже. Эти алгоритмы предполагают знание различных параметров системы, а именно, положительных целых чисел 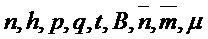 . Алгоритмы включают случайные выборы для матрицы
. Алгоритмы включают случайные выборы для матрицы 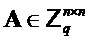 , как и для матрицы
, как и для матрицы 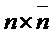
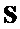 и матрицы
и матрицы 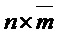
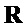 , причем все столбцы обеих входят в
, причем все столбцы обеих входят в 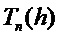 . Т. е. обе
. Т. е. обе 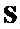 и
и 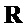 являются троичными матрицами, у которых каждый столбец имеет вес Хэмминга
являются троичными матрицами, у которых каждый столбец имеет вес Хэмминга 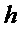 . Для выбора
. Для выбора 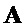 в явном виде системные параметры содержат случайное пространство
в явном виде системные параметры содержат случайное пространство 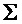 и отображение
и отображение 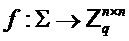 . Аналогичным образом для выбора
. Аналогичным образом для выбора 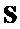 и
и 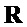 явным образом определены функции
явным образом определены функции 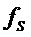 и
и 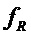 , которые на входах из
, которые на входах из 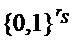 и
и 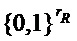 , соответственно, формируют троичные
, соответственно, формируют троичные 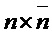 и
и 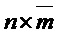 , соответственно, каждый столбец которых имеет вес Хэмминга
, соответственно, каждый столбец которых имеет вес Хэмминга 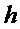 . Для множества
. Для множества 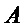 обозначим с помощью
обозначим с помощью  , что
, что 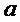 выводится равномерно из
выводится равномерно из 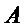 .
.
Первый алгоритм формирует открытый ключ 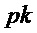 в
в 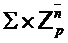 и секретный ключ
и секретный ключ 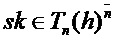 , т. е. троичную матрицу
, т. е. троичную матрицу 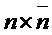 , столбцы которой имеют вес Хэмминга
, столбцы которой имеют вес Хэмминга 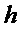 .
.
Алгоритм 1: PST.NR.CPA-PKE.Keygeneration()
Parameters Integers 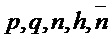
Input -
Output 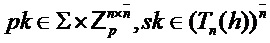

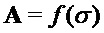
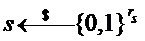
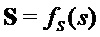
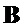 = Compress
= Compress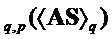
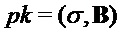
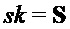
return 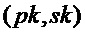
Следующий алгоритм формирует из открытого ключа 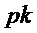 , сообщения
, сообщения 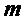 и случайной величины
и случайной величины 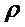 шифртекст
шифртекст 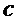 .
.
Алгоритм 2: PST.NR.CPA-PKE.Encryptwithrho(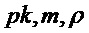 )
)
Parameters Integers 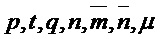
Input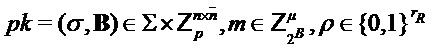
Output 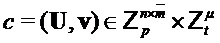
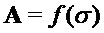
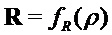
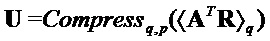
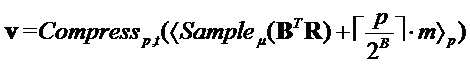
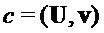
return 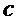
Алгоритм шифрования формирует из открытого ключа 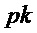 и сообщения
и сообщения 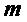 шифртекст
шифртекст 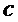 .
.
Алгоритм 3: PST.NR.CPA-PKE.Encrypt(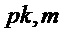 )
)
Parameters Integers 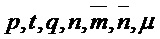
Input 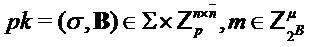
Output 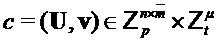
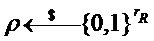
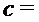 PST.NR.CPA-PKE.Encryptwithro(
PST.NR.CPA-PKE.Encryptwithro(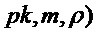
return 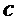
Алгоритм расшифрования получает обратно из секретного ключа 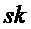 и шифртекста
и шифртекста 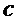 открытое сообщение
открытое сообщение 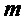 (оценку для него).
(оценку для него).
Алгоритм 4: PST.NR.CPA-PKE.Decrypt(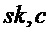 )
)
Parameters Integers 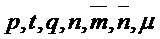
Input 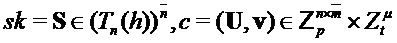
Output 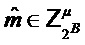
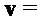 Decompress
Decompress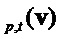
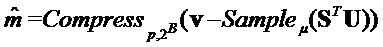
return 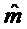
1.5 Механизм инкапсуляции ключа CPA для случая без кольца
Следующие три алгоритма построены на схеме шифрования открытого ключа, определенной в предыдущем разделе, для определения механизма инкапсуляции CPA-стойкого закрытого ключа. Он использует хэш-функцию 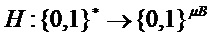 .
.
Примечание Можно было бы также использовать дополнительную хэш-функцию 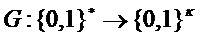 и применять
и применять 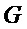 вместо
вместо 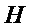 на этапе 4 алгоритма инкапсуляции и этапе 2 алгоритма декапсуляции.
на этапе 4 алгоритма инкапсуляции и этапе 2 алгоритма декапсуляции.
Алгоритм 5: PST.CPA-KEM.Keygeneration()
Parameters Integers 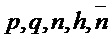
Input
Output 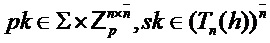
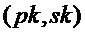 = PST.NR.CPA-PKE.Keygeneration()
= PST.NR.CPA-PKE.Keygeneration()
return 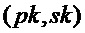
Как показано в алгоритме 5, формирование ключа для механизма инкапсуляции ключа может быть осуществлено путем выполнения формирования ключа схемы шифрования открытого ключа, например PST.NR.CPA-PKE.
Алгоритм 6: PST.CPA-KEM.Encapsulate(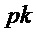 )
)
Parameters Integers 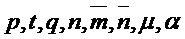
Input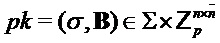
Output 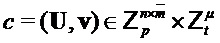 ,
, 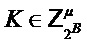
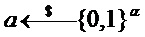
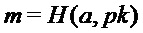
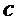 = PST.NR.CPA-PKE.Encrypt(
= PST.NR.CPA-PKE.Encrypt(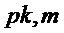 )
)
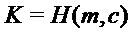
return 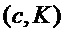
Как показано в алгоритме 6, инкапсуляция ключа может включать шифрование m, который может быть общим ключом, с использованием схемы шифрования открытого ключа, например PST.NR.CPA-KE. В данном алгоритмы биты m являются входом криптографической хэш-функции для получения результата K механизма инкапсуляции ключа, в данном случае в сочетании с c; альтернативные способы использования общих битов, например, в качестве входа в функцию выработки производного ключа, как рассмотрено ниже.
Алгоритм 7: PST.NR.CPA-KEM.Decapsulate(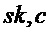 )
)
Parameters Integers 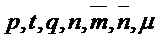
Input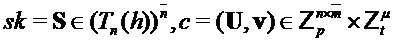
Output 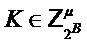
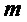 = PST.NR.CPA-PKE.Decrypt(
= PST.NR.CPA-PKE.Decrypt(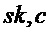 )
)
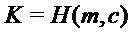
return 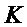
Как показано в алгоритме 7, функция декапсуляции ключа может включать расшифрование шифртекста c схемы шифрования открытого ключа, например, PST.NR.CPA-PKE, для получения открытого текста m, где m может быть общим ключом, и m совместно используют между узлом выполняющим инкапсуляцию и узлом, выполняющим декапсуляцию. Опять же, m может быть использован для получения результата K функции выработки производного ключа с использованием криптографической хэш-функции, как показано в алгоритме 7, или с использованием функции выработки производного ключа, как рассмотрено ниже.
Замечание Обратите внимание, что в алгоритмах 6 и 7 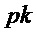 и
и 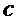 неявно отображают в битовую строку перед подачей их в
неявно отображают в битовую строку перед подачей их в 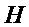 .
.
1.6 Платформа механизма инкапсуляции ключа CPA для случая без кольца
Платформу инкапсуляции ключа получают путем применения варианта KEM преобразования Фуджисаки-Окамото к нашей схеме шифрования, чтобы сделать ее CCA-устойчивой.
Использованы обозначения из схемы CPA-PKE. Также нужны две хэш-функции, 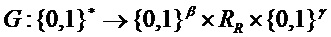 и
и 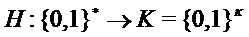 .
.
Сначала опишем алгоритм формирования ключа. Обратите внимание, что в случае равных случайных выборов открытые ключи 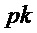 равны; секретный ключ, получаемый с помощью алгоритма 8, содержит секретный ключ, а также открытый ключ и случайную строку (
равны; секретный ключ, получаемый с помощью алгоритма 8, содержит секретный ключ, а также открытый ключ и случайную строку (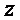 ).
).
Алгоритм 8: PST.NR.CCA-KEM.Keygen()
Parameters Integers 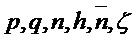
Input
Output - 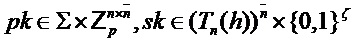
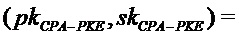 PST.NR.CPA-PKE.Keygen()
PST.NR.CPA-PKE.Keygen()
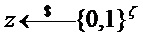
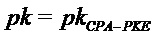
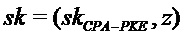
return 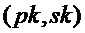
Выход 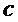 алгоритма 9 содержит, при равном входе с алгоритмом 3 и тем же выбором
алгоритма 9 содержит, при равном входе с алгоритмом 3 и тем же выбором 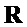 , шифртекст
, шифртекст 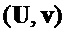 из алгоритма 3. Он также содержит ключ
из алгоритма 3. Он также содержит ключ 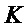 .
.
Алгоритм 9: PST.NR.CCA-KEM.Encapsulate(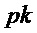 )
)
Parameters Integers 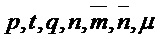
Input 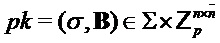
Output 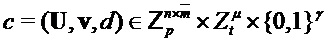
(строка 1) 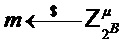
(строка 2) 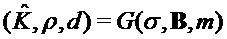
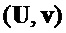 = PST.CPA.PKE.Encryptwithro(
= PST.CPA.PKE.Encryptwithro(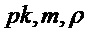 )
)
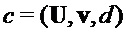
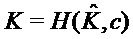
return 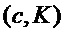
При равном секретном ключе 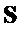 и равном входе
и равном входе 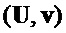 значение
значение 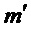 равно значению, получаемому при предоставлении их алгоритму 3. Мы делаем вывод, что если случайные выбора в алгоритмах NR CCA равны случайным выборам в алгоритмах NRCPA-PKE и алгоритмы NRCPA-PKE правильно извлекают сообщение
равно значению, получаемому при предоставлении их алгоритму 3. Мы делаем вывод, что если случайные выбора в алгоритмах NR CCA равны случайным выборам в алгоритмах NRCPA-PKE и алгоритмы NRCPA-PKE правильно извлекают сообщение 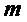 в строке 1 алгоритма 9, то
в строке 1 алгоритма 9, то 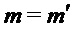 . В этому случае
. В этому случае 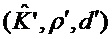 , вычисленные в строке 2 алгоритма 10, равны
, вычисленные в строке 2 алгоритма 10, равны 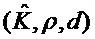 в строке 2 алгоритма 9, и поэтому значений
в строке 2 алгоритма 9, и поэтому значений 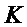 , вычисленные в строке 5 алгоритма 10 и алгоритма 9, равны. Если условие в строке 5 алгоритма 10 не удовлетворено, то выходом является случайный ключ.
, вычисленные в строке 5 алгоритма 10 и алгоритма 9, равны. Если условие в строке 5 алгоритма 10 не удовлетворено, то выходом является случайный ключ.
Алгоритм 10: PST.NR.CCA-KEM.Decapsulate(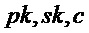 )
)
Parameters Integers 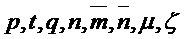
Input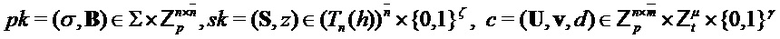
Output 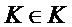
(строка 1) 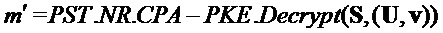
(строка 2) 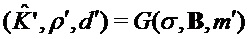
(строка 3) 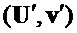 = PST.CPA-PKE.Encryptwithrho
= PST.CPA-PKE.Encryptwithrho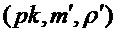
(строка 4) if 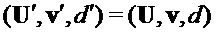 then
then
(строка 5) return 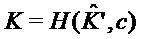
(строка 6) else
(строка 7) return 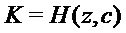
(строка 8) end if
Замечание В алгоритмах 9 и 10 в неявной форме отображают 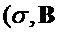 )
) 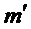 и
и 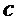 на двоичные строки перед подаче, затем в
на двоичные строки перед подаче, затем в 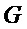 и
и 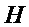 , соответственно.
, соответственно.
1.7 Объединенный случай без кольца и с кольцом
В данном разделе описана комбинированная версия без кольца и с кольцом предыдущего алгоритма с кольцом многочленов 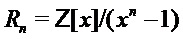 .
. 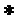 обозначает умножение в
обозначает умножение в 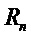 . Чтобы подчеркнуть схожесть со случаем без кольца, определим
. Чтобы подчеркнуть схожесть со случаем без кольца, определим 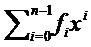 и вектор (столбцов)
и вектор (столбцов) 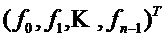 . Для
. Для 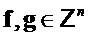 определим
определим 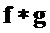 как вектор коэффициентов многочлена
как вектор коэффициентов многочлена 
 . Т. е. для
. Т. е. для 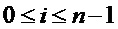
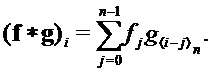
Также определим умножение 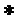 матриц следующем образом. Пусть
матриц следующем образом. Пусть 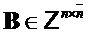 и пусть
и пусть 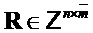 , скажем
, скажем
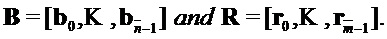
Матрица 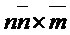
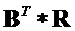 определяется как
определяется как
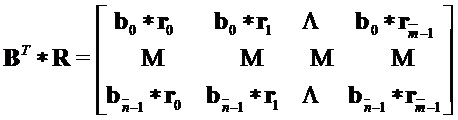
Чтобы различать случаи с кольцом и без кольца, используем булев параметр 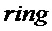 .
.
Алгоритм 11: PST.CPA-PKE.Keygeneration()
Parameters Integers 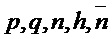 ; Boolean
; Boolean 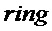 Requirement If
Requirement If 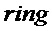 then
then 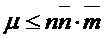 else
else 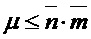
Input
Output - 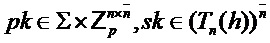
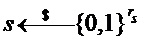
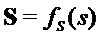

if 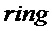
then begin 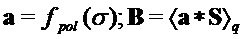 end
end
else begin 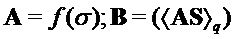 end
end
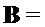 Compress
Compress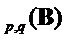
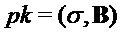
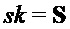
return 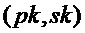
Как отмечалось выше, варианты реализации настоящего изобретения могут быть основаны на параметре сложности и параметре структуры для указания типа криптографии, подлежащей использованию. В настоящем алгоритме входной параметр n используют для обозначения размера выходных значений pk и sk, и в силу этого параметр сложности может быть использован как значение n. Аналогичным образом, параметр ring данного алгоритма используют для указания того, используется ли версия алгоритма с кольцом с кольцом 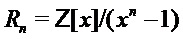 (и, следовательно, может быть установлена на True, если параметр структуры равен параметру n сложности) или используется версия алгоритма без кольца (и, следовательно, может быть установлена на False, если параметр структуры равен 1).
(и, следовательно, может быть установлена на True, если параметр структуры равен параметру n сложности) или используется версия алгоритма без кольца (и, следовательно, может быть установлена на False, если параметр структуры равен 1).
Как в случае с кольцом, так и в случае без кольца алгоритм использует матрицу a или A размера, равного параметру сложности, деленному на параметр структуры, причем элементы являются целочисленными многочленами степени меньше параметра структуры, а матрица может быть общей матрицей. В частности, в случае с кольцом, как упомянуто выше, параметр структуры может быть равен параметру сложности, в каковом случае матрица a может содержать один многочлен степени n, соответствующий (благодаря вышеупомянутой идентификации многочленов с помощью векторов) вектору длины n, как показано в алгоритме 11. В случае без кольца параметр структуры может быть равен 1, так что матрица A имеет размер, равный параметру сложности и содержит многочлены степени меньше единицы, например целые числа. В обоих случай a или A формирование из значения σ с использованием функции f, где σ может быть начальным числом, а оценка f может включать оценку детерминированного генератора псевдослучайных чисел.
В алгоритме 11 матрицу S, которая может быть матрицей закрытого ключа, формируют из области 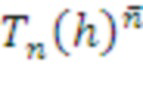
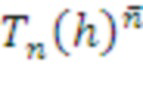 , т. е. с помощью элементов, являющихся троичными матрицами
, т. е. с помощью элементов, являющихся троичными матрицами 
 на
на 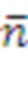
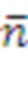 , соответствующей (благодаря вышеупомянутой идентификации многочленов с помощью векторов) матрице, содержащей целочисленные многочлены степени меньше структурного параметра.
, соответствующей (благодаря вышеупомянутой идентификации многочленов с помощью векторов) матрице, содержащей целочисленные многочлены степени меньше структурного параметра.
Далее, алгоритм формирует матрицу B, которая может быть матрицей открытого ключа, путем вычисления матричного произведения между матрицей a или A (которая может быть общей матрицей) и S (которая может быть матрицей закрытого ключа). В таком варианте реализации, как описано выше, может быть использована оптимизированная реализация вычисления открытого ключа a * S или AS. В случае с кольцом операции умножения многочленов a*S могут быть выражены матрицей n × n и вектором элементов длины n с элементами из Zq. В случае без кольца AS тоже является произведением матриц с размером A, равным параметру сложности. Вследствие этого в некоторых вариантах реализации, где используют оптимизированную реализацию операции открытого ключа, общая часть, относящаяся к умножению матриц, может быть вызвана для разных значений параметра структуры и/или параметра сложности. Вне зависимости от этого варианты реализации, использующие алгоритм 11, могут формировать B (которая может быть матрицей открытого ключа) путем вычисления матричного произведения между матрицей a или A (которая может быть общей матрицей) и S (которая может быть матрицей закрытого ключа) по модулю первого модуля, и по модулю многочлена приведения, имеющего степень, равную параметру структуры, и добавления шума к элементам в произведении матрицы, причем добавление шума в данном варианте реализации включает умножение каждого немасштабированного элемента на p, деление на q, округление до целого числа (например, ближайшего целого числа) и взятие округленного элемента по модулю p.
Наконец, алгоритм возвращает значения (σ,B) и S, так что в итоговой операции шифрования открытого ключа открытый ключ может содержать B и значение σ, из которых можно получить a или A, а закрытый ключ может содержать S.
Следующий алгоритм формирует из открытого ключа 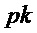 , сообщения
, сообщения 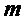 и случайной величины
и случайной величины 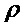 шифртекст
шифртекст 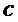 , содержащий первую часть шифртекста и вторую часть шифртекста.
, содержащий первую часть шифртекста и вторую часть шифртекста.
Алгоритм 12: PST.CPA-PKE.Encryptwithrho(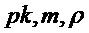 )
)
Parameters Integers 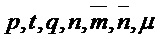 ; Boolean
; Boolean 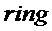 Requirement If
Requirement If 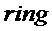 then
then 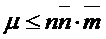 else
else 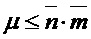
Input 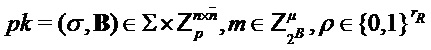
Output 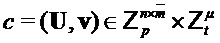
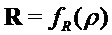
if
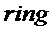
then begin 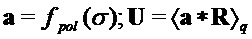 end
end
else begin 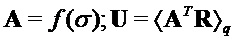 end
end
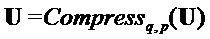
if 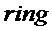
then 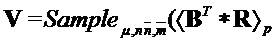 )
)
else 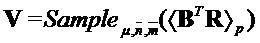 ;
;
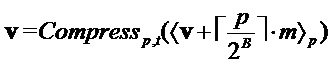
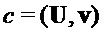
return 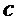
Как показано, алгоритм сначала получает a или A, которая может быть общей матрицей, путем формирования из выхода детерминированного генератора псевдослучайных чисел с использованием σ из pk в качестве начального числа. Следовательно, открытый ключ схемы шифрования открытого ключа может содержать начальное число, из которого нужно получить общую матрицу. Кроме того, он формирует значение 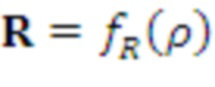
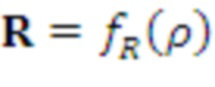 , которое может быть закрытой матрицей. Как и в алгоритме 11, a или A представляет собой квадратную матрицу размера, равного параметру сложности, деленному на параметр структуры, причем элементы являются многочленами степени меньше параметра структуры, а R представляет собой матрицу с элементами, являющимися целочисленными многочленами степени меньше параметра структуры. Кроме того, как и в алгоритме 12, вычисляют матрицу U, которая может быть первой частью шифртекста, путем вычисления матричного произведения между матрицей a или A и R по модулю q и модулю многочлена приведения степени, равной параметру сложности, и последующего добавления шума, включающего умножение каждого немасштабированного элемента на p, деление на q, округление до целого числа (например, ближайшего целого числа) и взятие округленного элемента по модулю p.
, которое может быть закрытой матрицей. Как и в алгоритме 11, a или A представляет собой квадратную матрицу размера, равного параметру сложности, деленному на параметр структуры, причем элементы являются многочленами степени меньше параметра структуры, а R представляет собой матрицу с элементами, являющимися целочисленными многочленами степени меньше параметра структуры. Кроме того, как и в алгоритме 12, вычисляют матрицу U, которая может быть первой частью шифртекста, путем вычисления матричного произведения между матрицей a или A и R по модулю q и модулю многочлена приведения степени, равной параметру сложности, и последующего добавления шума, включающего умножение каждого немасштабированного элемента на p, деление на q, округление до целого числа (например, ближайшего целого числа) и взятие округленного элемента по модулю p.
Далее, алгоритм использует значение B из pk, которое может быть матрицей открытого ключа. Следовательно, открытый ключ схемы шифрования открытого ключа может дополнительно содержать матрицу открытого ключа сетевого узла, соответствующего pk. Исходя из этого, вычисляют значение 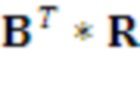
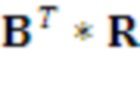 (в случае с кольцом) или
(в случае с кольцом) или 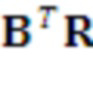
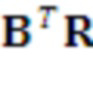 (в случае без кольца), которое может быть необработанным ключом, т. е. матричное произведение между B и R, где B и R рассматривают как многочлены степени меньше параметра структуры. Как отмечалось, в некоторых вариантах реализации та же самая идея перестановки, что и для матрицы открытого ключа, может быть применена к данному вычислению, так что общая часть, относящаяся к умножению, может быть использована для других значений параметра структуры и/или параметра сложности.
(в случае без кольца), которое может быть необработанным ключом, т. е. матричное произведение между B и R, где B и R рассматривают как многочлены степени меньше параметра структуры. Как отмечалось, в некоторых вариантах реализации та же самая идея перестановки, что и для матрицы открытого ключа, может быть применена к данному вычислению, так что общая часть, относящаяся к умножению, может быть использована для других значений параметра структуры и/или параметра сложности.
Наконец, алгоритм вычисляет значение v, которое может быть второй частью шифртекста, из значения 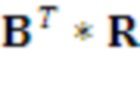
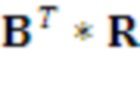 или
или 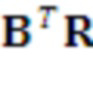
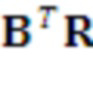 и из сообщения m, которое может быть, например, открытым сообщением или, в случае использования в механизме инкапсуляции, таком как PST.CPA-KEM или PST.NR.CCA-KEM, общим ключом между двумя сторонами, из которого можно вывести ключ, используемый в последующем обмене данными. Значение v возвращается вместе с U из алгоритма, так что эти значения вместе могут быть отправлены сетевому узлу, соответствующему данному pk.
и из сообщения m, которое может быть, например, открытым сообщением или, в случае использования в механизме инкапсуляции, таком как PST.CPA-KEM или PST.NR.CCA-KEM, общим ключом между двумя сторонами, из которого можно вывести ключ, используемый в последующем обмене данными. Значение v возвращается вместе с U из алгоритма, так что эти значения вместе могут быть отправлены сетевому узлу, соответствующему данному pk.
Алгоритм шифрования, приведенный ниже, формирует из открытого ключа 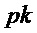 и сообщения
и сообщения 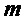 шифртекст
шифртекст 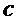 . Данный алгоритм непосредственно вызывает алгоритм 12, так что варианты реализации, использующие алгоритм 13, могут аналогичным образом принимать параметр сложности и параметр сложности, получать общую матрицу, формировать закрытую матрицу, формировать первую часть шифртекста и вычислять вторую часть шифртекста, как указано выше, а в вариантах реализации операции шифрования открытого ключа, основанных на алгоритме 13, открытый ключ может, таким образом, содержать матрицу открытого ключа и данные, из которых может быть получена общая матрица, а закрытый ключ может содержать матрицу закрытого ключа.
. Данный алгоритм непосредственно вызывает алгоритм 12, так что варианты реализации, использующие алгоритм 13, могут аналогичным образом принимать параметр сложности и параметр сложности, получать общую матрицу, формировать закрытую матрицу, формировать первую часть шифртекста и вычислять вторую часть шифртекста, как указано выше, а в вариантах реализации операции шифрования открытого ключа, основанных на алгоритме 13, открытый ключ может, таким образом, содержать матрицу открытого ключа и данные, из которых может быть получена общая матрица, а закрытый ключ может содержать матрицу закрытого ключа.
Алгоритм 13: PST.CPA-PKE.Encrypt(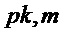 )
)
Parameters Integers 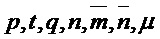 , Boolean
, Boolean 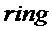
Input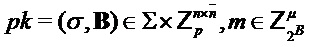
Output 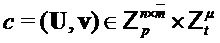
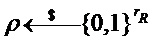
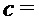 PST.CPA-PKE.Encryptwithro(
PST.CPA-PKE.Encryptwithro(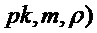
return 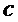
Алгоритмы, такие как PST.CPA-KEM.Encapsulate(), могут использовать PST.CPA-PKE.Encrypt или PST.CPA-PKE.Encryptwithrho в контексте обмена ключами или механизма инкапсуляции ключа. В этом случае U брать на себя роль матрицы открытого ключа стороны, выполняющей инкапсуляцию, а R может брать на себя роль соответствующей матрицы закрытого ключа. Аналогичным образом, v может брать на себя роль данных согласования, чтобы для инкапсулирующего устройства и декапсулирующего устройства поступал один и тот же общий ключ.
Алгоритм расшифрования получает обратно из секретного ключа 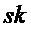 и шифртекста
и шифртекста 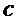 открытое сообщение
открытое сообщение 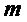 (оценку для него).
(оценку для него).
Алгоритм 14: PST.CPA-PKE.Decrypt(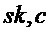 )
)
Parameters Integers 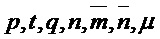 ; Boolean:
; Boolean: 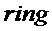 Requirement If
Requirement If 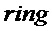 then
then 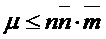 else
else 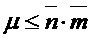
Input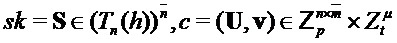
Output 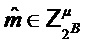
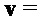 Decompress
Decompress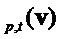
if 
then 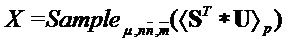
else 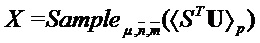
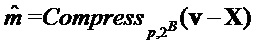
return 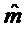
Аналогично вышеприведенным алгоритмам алгоритм 14 принимает в качестве входных параметров значение n, указывающее размер входного sk, и значение ring, указывающее, нужно ли использовать вариант с кольцом или без кольца, например, в вариантах реализации, использующих алгоритм 14, n может соответствовать параметру сложности, а ring может указывать, равен ли параметр сложности параметру структуры или нет. Алгоритм получает в качестве входа матрицу S с элементами посредством соответствия между векторами и многочленами степени n, рассмотренными ниже, которые являются целочисленными многочленами степени меньше параметра структуры, причем S может быть матрицей закрытого ключа самого узла. Алгоритм получает в качестве еще одного входа матрицу U, которая может быть первой частью шифртекста, и вычисляет 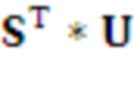
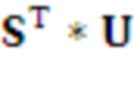 (в случае с кольцом) или
(в случае с кольцом) или 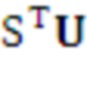
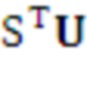 (в случае без кольца), которая может быть необработанным ключом, и которую вычисляют как матричное произведение между S и U, причем обе матрицы рассматриваются как матрицы, содержащие многочлены степени не больше параметра структуры. Затем алгоритм использует произведение матриц, например, значение
(в случае без кольца), которая может быть необработанным ключом, и которую вычисляют как матричное произведение между S и U, причем обе матрицы рассматриваются как матрицы, содержащие многочлены степени не больше параметра структуры. Затем алгоритм использует произведение матриц, например, значение 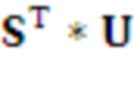
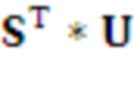 или
или 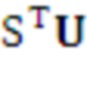
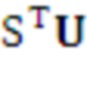 , и другое значение v, принятое в качестве входа, которое может быть второй частью шифртекста, для получения сообщения
, и другое значение v, принятое в качестве входа, которое может быть второй частью шифртекста, для получения сообщения 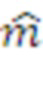
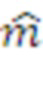 путем использования процедур Sample и Compress. Как и в PST.CPA-PKE.Encryptwithrho сообщение
путем использования процедур Sample и Compress. Как и в PST.CPA-PKE.Encryptwithrho сообщение 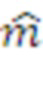
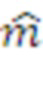 может содержать общий ключ в механизме обмена ключами, из которого выводят ключ одним из способов, подробно описанных ниже, для последующего обмена данными.
может содержать общий ключ в механизме обмена ключами, из которого выводят ключ одним из способов, подробно описанных ниже, для последующего обмена данными.
Как отмечалось выше, PST.CPA-PKE.Decrypt может быть использован алгоритмами, такими как PST.NR.CPA-KEM.DecapsulateВ, в контексте инкапсуляции ключа или обмена ключами. В этом случае U может быть матрицей открытого ключа стороны, выполняющей инкапсуляцию, например, шифрование PST.CPA-PKE.Encrypt; а v может быть данными согласования, чтобы на оба узла поступало одно и то же значение для 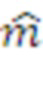
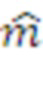 , которое может быть сообщением, общим ключом или данными, для которых выводят общий ключ при последующем обмене данными, например, как подробно описано для PST.NR.CPA-KEM.Decapsulate.
, которое может быть сообщением, общим ключом или данными, для которых выводят общий ключ при последующем обмене данными, например, как подробно описано для PST.NR.CPA-KEM.Decapsulate.
1.7.1 Конфигурации платформы
Приведенные выше алгоритмы позволяют обеспечивать несколько алгоритмов в зависимости от параметров конфигурации.
• CPA-KEM на основе LWR - для n = 1 и k = d.
• CPA-KEM на основе RLWR - для n = d и k = 1.
• CCA-KEM на основе LWR - для n = 1 и k = d.
• CCA-KEM на основе RLWR - для n = d и k = 1.
• CCA-KEM-DEM на основе LWR - для n = 1 и k = d.
• CCA-KEM-DEM на основе RLWR - для n = d и k = 1.
На Фиг. 1 схематически показан пример варианта реализации сети 100 с выработкой общего ключа. Выработка общего ключа является примером криптографической операции. При выработке общего ключа используют ряд элементов, например, построение общей матрицы, матрицы закрытого ключа, матрицы открытого ключа, умножение матриц, добавление шума и т. д., которые являются общими для других типов криптографических операций, например шифрования открытого ключа. В варианте реализации устройство 100 может быть переконфигурировано для других типов криптографических операций, например, как указано выше, или как указано в литературе. В варианте реализации устройство 100 может быть переконфигурировано для нескольких типов криптографических операций. В любом случае устройство 100 имеет преимущество, заключающееся в том, что доступны множество разных уровней структуры и сложности. Например, криптографическая операция может быть одной из следующих: протокол обмена ключами (KEX), механизм инкапсуляции ключа (KEM), шифрование открытого ключа (PKE), цифровая подпись. В варианте реализации первый сетевой узел может быть выполнен с возможностью приема селектора, выбирающего криптографическую операцию из множества разных криптографических операций. Однако в качестве примера варианты осуществления, приведенные ниже, предполагают, что устройство 100 выполнено с возможностью выработки общего ключа.
На Фиг. 1 показаны два сетевых узла в системе: сетевой узел 110 типа инициатора и сетевой узел 210 типа ответчика. В варианте реализации системы выработки общего ключа количество узлов может быть больше, даже намного больше, чем два, например, более 1000 узлов, например, больше 10^6 узлов.
Разницам между сетевым узлом типа инициатора и типа ответчика заключается в том, как они поступают с данными согласования. Сетевой узел типа инициатора принимает данные согласования и применяет их для получения общего ключа, тогда как сетевой узел типа ответчика формирует данные согласования и отправляет их сетевому узлу типа инициатора. Для получения общего ключа сетевому узлу типа ответчика не нужны данные согласования. Как правило, инициатор будет также инициировать протокол выработки общего ключа между двумя сетевыми узлами, т. к. это может сократить количество циклов протокола, выполняемых между двумя сетевыми узлами. Однако это не обязательно - протокол выработки общего ключа может быть также инициирован сетевым узлом типа ответчика.
Кроме того, в варианте реализации сетевого узла сетевой узел выполнен с возможностью функционирования в соответствии с режимом инициатора и в соответствии с режимом ответчика. Например, если сетевой узел инициирует выработку общего ключа, например, отправляет сообщение другому сетевому узлу, сигнализируя о начале протокола выработки общего ключа, то этот сетевой узел может переключиться в режим инициатора. Если сетевой узел отвечает на выработку общего ключа, например, принимает сообщение от другого сетевого узла, сигнализируя о начале протокола выработки общего ключа, то этот сетевой узел может переключиться в режим ответчика. Хотя это удобно на практике, этот вариант тоже не является строго обязательным; например, в системе выработки общего ключа некоторые узлы могут быть сконфигурированы только как инициатор, а некоторые могут быть сконфигурированы только как узлы-ответчики. В результате некоторые узлы не смогут вырабатывать общий ключ совместно. Для некоторых сетей это необязательно будет проблемой, например, в самоорганизующейся сети (ad-hoc сеть) или самоорганизующихся беспроводных ячеистых сетях (ad-hoc wireless grid) и т. д., при условии, что достаточно много пар сетевых узлов могут обмениваться данными и вырабатывать общий ключ.
Узел-инициатор 110 содержит интерфейс 120 связи. Узел-ответчик 210 содержит интерфейс 220 связи. Интерфейсы связи могут быть выполнены с возможностью цифрового обмена данными с другими узлами в системе выработки общего ключа. Однако не обязательно, что все узлы в системе могут быть доступны в любое время.
Интерфейсы 120 и 220 связи выполнены с возможностью цифрового обмена данными. Например, интерфейсы связи могут быть выполнены с возможностью обмена данными по компьютерной сети. Например, интерфейс связи может быть выполнен с возможностью беспроводного, например, Wi-Fi, ZigBee, Bluetooth и т. п., и/или проводного, например, Ethernet, USB и т. п., обмена данными. Обмен данными между узлами 110 и 210 может быть также комбинацией проводных и беспроводных соединений. Например, узлы в системе 100, содержащей узлы 110 и 210, могут содержать электронное запоминающее устройство, которое содержит идентификатор связи, единственным образом определяющий узел в пределах системы 100. Например, идентификатор связи может быть включен в цифровые сообщения, которыми обмениваются узлы 110 и 210, например для адресации сообщения. Например, идентификатор связи может быть IP-адресом, MAC-адресом и т. п.
Узел электронной сети выполнен с возможностью осуществления протокола обмена ключами (KEX). Проток включает обмен сообщениями между узлами 110 и 210 посредством интерфейсов 120 и 220 связи и выполнение вычислений, например, на данных, принимаемых с другого узла. Исполнение протокола выработки общего ключа реализуют в схеме процессора, примеры которой показаны ниже. На Фиг. 1 показаны функциональные блоки, которые могут быть функциональными блоками схемы процессора. Например, Фиг. 1 может быть использована в качестве примерного плана возможной функциональной организации схемы процессора. Схема процессора не показана отдельно от блоков на Фиг. 1. Например, функциональные блоки, показанные на Фиг. 1, могут быть также полностью или частично реализованы в компьютерных инструкциях, которые хранятся на сетевых узлах и выполнены с возможностью исполнения микропроцессором сетевого узла.
Узел-инициатор 110 и узел-ответчик 210 выполнены с возможностью выполнения протокола обмена ключами (KEX). Схемы KEX включают обмен открытыми данными, часто называемыми открытыми ключами, каждой стороной, которые затем независимо используются другой стороной наряду с их собственными закрытыми данными, часто называемыми секретным ключом для вычисления общего совместного ключа. Интересной особенностью некоторых вариантов реализации является то, что стороны не обмениваются никогда фактическим конечным общим секретом, даже в зашифрованном виде, а две стороны вычисляют его независимо на каждом конце. В результате достигают требуемого свойства, известному как прямая секретность, которое гарантирует, что даже вскрытие злоумышленником долгосрочных секретных ключей какой-либо стороны в будущем не поставит под угрозу секретность зашифрованных сообщений, которыми обменивались в прошлом.
Варианты реализации не опираются на обеспечение конфиденциального обмена данных доверенной третьей стороной. Канал связи между интерфейсами 120 и 220 связи необязательно должен быть закрытым каналом. Злоумышленники могут быть в состоянии прослушивать канал связи. Несмотря на это, совместно выработанный узлами 110 и 210, может быть защищенным. Если канал связи защищен от изменений, то степень аутентификации может быть получена в той мере, в какой она обеспечивается каналом. Однако, если канал между интерфейсами 120 и 220 связи не защищен от изменений, схема KEX не достигнет аутентификации. Для получения аутентификации варианты реализации могут быть объединены с известным механизмом аутентификации, например, неявным механизмом аутентификации, например, с использованием сертифицированных открытых ключей, или явным механизмом аутентификации, например, с использованием цифровых подписей.
Узел-инициатор 110 содержит блок 130 общей матрицы. Узел-ответчик 210 содержит блок 230 общей матрицы. Узлы 130 и 230 общей матрицы выполнены с возможностью получения общей матрицы (
 ), совместно используемой между двумя узлами. Существует множество способов обеспечения совместного использования одной и той же матрицы между узлами 110 и 210, особенно с учетом того факта, что матрица A необязательно должна оставаться закрытой для узлов 110 и 210.
), совместно используемой между двумя узлами. Существует множество способов обеспечения совместного использования одной и той же матрицы между узлами 110 и 210, особенно с учетом того факта, что матрица A необязательно должна оставаться закрытой для узлов 110 и 210.
Узел 130 общей матрицы и узел 230 общей матрицы выполнены с возможностью приема в качестве вход параметра 
 сложности и параметра
сложности и параметра 
 структуры. На Фиг. 1 параметр
структуры. На Фиг. 1 параметр 
 сложности и параметр
сложности и параметр 
 структуры схематически указаны номером позиции 131. Следует отметить, что оба узла принимают одинаковые параметр
структуры схематически указаны номером позиции 131. Следует отметить, что оба узла принимают одинаковые параметр 
 сложности и параметр
сложности и параметр 
 структуры. Эти числа
структуры. Эти числа 
 и
и 
 определяют размер и тип элементов матрицы
определяют размер и тип элементов матрицы 
 . Устройства 110 и 210 могут быть также выполнены с возможностью приема селектора, выбирающего криптографическую операцию.
. Устройства 110 и 210 могут быть также выполнены с возможностью приема селектора, выбирающего криптографическую операцию.
Например, параметр 
 сложности и параметр
сложности и параметр 
 структуры могут быть установлены посредством API, например, приложением, которое использует устройства 110 и 210, например, для закрытого обмена данными. Приложение может принимать решение относительно требуемой сложности и структуры и инструктировать устройство 110 и/или 210 посредством, например, вызова функции.
структуры могут быть установлены посредством API, например, приложением, которое использует устройства 110 и 210, например, для закрытого обмена данными. Приложение может принимать решение относительно требуемой сложности и структуры и инструктировать устройство 110 и/или 210 посредством, например, вызова функции.
Элементы в общей матрице 
 предпочтительно выбраны по модулю первого модуля
предпочтительно выбраны по модулю первого модуля 
 , по модулю многочлена (
, по модулю многочлена (
 ) приведения степени, равной параметру структуры (
) приведения степени, равной параметру структуры (
 ). Если n = 1, элементы являются целыми числами; если
). Если n = 1, элементы являются целыми числами; если 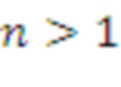
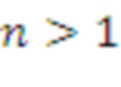 , они представляют собой многочлены. Первый модуль
, они представляют собой многочлены. Первый модуль 
 и многочлен
и многочлен 
 приведения тоже совместно используются узлом 110 и узлом 210, например, передаются или предварительно определяются. Общая матрица
приведения тоже совместно используются узлом 110 и узлом 210, например, передаются или предварительно определяются. Общая матрица 
 представляет собой квадратную матрицу
представляет собой квадратную матрицу 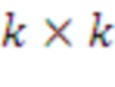
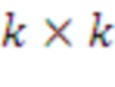 , например, размера
, например, размера 
 . Количество строк и столбцов
. Количество строк и столбцов 
 равно параметру
равно параметру 
 сложности, деленному на параметр
сложности, деленному на параметр 
 структуры. Если
структуры. Если 
 , матрица
, матрица 
 имеет один элемент-многочлен. На практике в качестве многочлена
имеет один элемент-многочлен. На практике в качестве многочлена 
 приведения выбирают, например,
приведения выбирают, например, 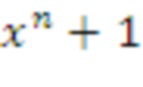
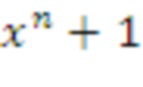 ,
, 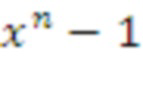
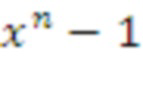 или
или 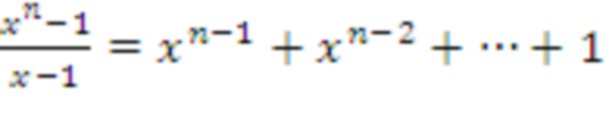
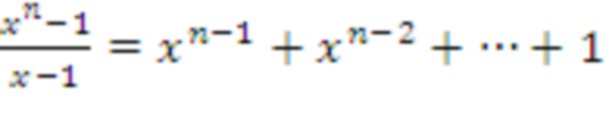 .
.
Предпочтительно параметр 
 структуры делит параметр
структуры делит параметр 
 сложности, так что можно вычислить размер
сложности, так что можно вычислить размер 
 . Однако в варианте реализации
. Однако в варианте реализации 
 получают путем округления параметра
получают путем округления параметра 
 сложности, деленного на параметр
сложности, деленного на параметр 
 структуры, например, округления до ближайшего целого числа, округления вверх или округления вниз.
структуры, например, округления до ближайшего целого числа, округления вверх или округления вниз.
В варианте реализации устройства 110 и 210 выполнены с возможностью приема разных параметров 
 сложности и/или разных параметров
сложности и/или разных параметров 
 структуры. Например, устройства могут допускать любые параметры
структуры. Например, устройства могут допускать любые параметры 
 сложности, например, вплоть до некоторой верхней границы и/или выше некоторой нижней границы. Кроме того, устройство может допускать n = 1 или n = d, или в более общем смысле, любое
сложности, например, вплоть до некоторой верхней границы и/или выше некоторой нижней границы. Кроме того, устройство может допускать n = 1 или n = d, или в более общем смысле, любое 
 , которое делит
, которое делит 
 , и для которого
, и для которого 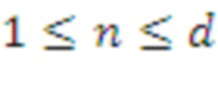
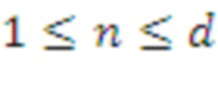 .
.
Что интересно, даже при приеме разных параметров узлам не нужно иметь различные реализации для разных значений параметра. Например, узлы 110 и 210 могут быть выполнены с возможностью вызова общей части, относящейся к умножению матриц, для разных значений параметра 
 структуры и/или параметра
структуры и/или параметра 
 сложности.
сложности.
В варианте реализации параметр 
 структуры ограничен таким образом, что n или n + 1 является простым числом, но это не обязательно. В варианте реализации параметр
структуры ограничен таким образом, что n или n + 1 является простым числом, но это не обязательно. В варианте реализации параметр 
 структуры является степенью числа 2, а первый модуль
структуры является степенью числа 2, а первый модуль 
 представляет собой простое число, но это тоже не обязательно.
представляет собой простое число, но это тоже не обязательно.
Например, один из узлов, скажем, узел-инициатор 110, может выбирать в блоке 130 общей матрицы матрицу A, например, случайным образом с элементами по модулю 
 и модулю
и модулю 
 . После этого элементы могут быть отправлены посредством блоков связи на другой узле, например, в блок 230 общей матрицы. В данном случае последний блок 230 общей матрицы будет просто принимать матрицу и сохранять ее. Матрица A может быть также выбрана узлом-ответчиком 210, а не отправлена узлом-инициатором 110.
. После этого элементы могут быть отправлены посредством блоков связи на другой узле, например, в блок 230 общей матрицы. В данном случае последний блок 230 общей матрицы будет просто принимать матрицу и сохранять ее. Матрица A может быть также выбрана узлом-ответчиком 210, а не отправлена узлом-инициатором 110.
Эти два узла могут взаимодействовать при выборе матрицы A. Например, каждый узел может выбрать некоторые из элементов и отправить их другой стороне. Например, узлы-инициаторы могут выбирать нечетные элементы, а узел-ответчик - четные элементы и т. д. Таким образом, ни один из двух узлов не имеет контроля над конечной матрицей A. Например, каждый двух узлов может выбрать всю матрицу A и сообщить ее другой стороне. Затем эти две матрицы могут быть сложены по модулю 
 и
и 
 . Чтобы последний узел не посылал матрицу заранее, сначала этому последнему узлу может быть отправлена фиксация транзакции по выбранной матрице.
. Чтобы последний узел не посылал матрицу заранее, сначала этому последнему узлу может быть отправлена фиксация транзакции по выбранной матрице.
Интересным способом сокращения служебных данных отправки полной матрицы 
 является формирование случайного начального числа и отправка этого случайного начального числа через канал связи другому узлу. После приема начального числа первый и второй сетевые узлы могут использовать ее для формирования матрицы
является формирование случайного начального числа и отправка этого случайного начального числа через канал связи другому узлу. После приема начального числа первый и второй сетевые узлы могут использовать ее для формирования матрицы 
 любым вышеуказанным способом. То же самое случайное начальное число может быть использовано для затравки детерминированного генератора псевдослучайных чисел, который, в свою очередь, формирует матрицу (
любым вышеуказанным способом. То же самое случайное начальное число может быть использовано для затравки детерминированного генератора псевдослучайных чисел, который, в свою очередь, формирует матрицу (
 ) из выхода генератора псевдослучайных чисел. Как указано выше, каждый узел может отправлять начальное число, например, для формирования разных частей
) из выхода генератора псевдослучайных чисел. Как указано выше, каждый узел может отправлять начальное число, например, для формирования разных частей 
 , или два начальных числа могут быть объединены, например, посредством сложения или «исключающего или» (XOR) и т. д., и объединенное начальное число может быть использовано для формирования
, или два начальных числа могут быть объединены, например, посредством сложения или «исключающего или» (XOR) и т. д., и объединенное начальное число может быть использовано для формирования 
 .
.
Начальные числа могут быть, например, выбраны из еще одного генератора случайных числе, например, генератора истинно случайных чисел. Узлы также могут быть выполнены со списком случайных числе, например при изготовлении. В этом случае узлы выбирают следующее случайное число из списка при каждом формировании новой матрицы 
 для новой выработки общего ключа. В случае исчерпания списка случайных чисел он может быть пополнен из доверенного источника.
для новой выработки общего ключа. В случае исчерпания списка случайных чисел он может быть пополнен из доверенного источника.
В варианте реализации элементы 
 выбирают из вектора
выбирают из вектора 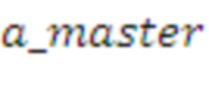
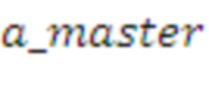 . В варианте реализации матрицу
. В варианте реализации матрицу 
 изменяют после каждого использования, например, применяют перестановку, либо могут быть заменены один или более элементов.
изменяют после каждого использования, например, применяют перестановку, либо могут быть заменены один или более элементов.
Узел-инициатор 110 содержит блок 140 матрицы закрытого ключа. Узел-ответчик 210 содержит блок 240 матрицы закрытого ключа. Блок 140 матрицы закрытого ключа выполнен с возможностью формирования матрицы 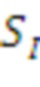
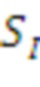 закрытого ключа; блок 240 матрицы закрытого ключа выполнен с возможностью формирования матрицы
закрытого ключа; блок 240 матрицы закрытого ключа выполнен с возможностью формирования матрицы 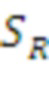
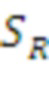 закрытого ключа. Элементы в матрицах закрытого ключа представляют собой целочисленные многочлены степени не боле n. Если степень
закрытого ключа. Элементы в матрицах закрытого ключа представляют собой целочисленные многочлены степени не боле n. Если степень 
 равна 1, то по сути элементы являются целыми числами.
равна 1, то по сути элементы являются целыми числами.
Вообще говоря, матрицу закрытого ключа выбирают случайным образом. Например, элементы в матрице закрытого ключа (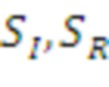
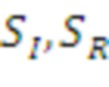 ) могут быть выбраны из равномерного случайного вероятностного распределения. Распределение может быть также не равномерным, например, когда вероятность нулевого элемента выше вероятности ненулевого элемента, например, по меньшей мере в два раза.
) могут быть выбраны из равномерного случайного вероятностного распределения. Распределение может быть также не равномерным, например, когда вероятность нулевого элемента выше вероятности ненулевого элемента, например, по меньшей мере в два раза.
На матрицу закрытого ключа могут быть наложены различные ограничения, например, для улучшения безопасности или для уменьшения размера ее данных. Матрица закрытого ключа (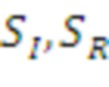
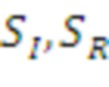 ) может быть выбрана равномерным случайным образом потенциально возможных матриц закрытого ключа, например, в пределах ограничений. Например, в варианте реализации коэффициенты элементов в матрице закрытого ключа ограничивают по абсолютному значению посредством границы (границы), например, когда упомянутая граница равна 2 (
) может быть выбрана равномерным случайным образом потенциально возможных матриц закрытого ключа, например, в пределах ограничений. Например, в варианте реализации коэффициенты элементов в матрице закрытого ключа ограничивают по абсолютному значению посредством границы (границы), например, когда упомянутая граница равна 2 (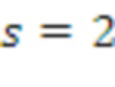
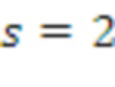 ), или когда граница равна 1 (
), или когда граница равна 1 (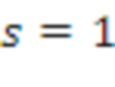
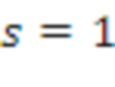 ), причем последний случай соответствует двоичным числам со знаком. Например, столбцы и/или строки закрытого ключа (
), причем последний случай соответствует двоичным числам со знаком. Например, столбцы и/или строки закрытого ключа (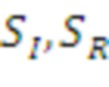
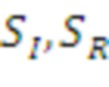 ) имеют фиксированный или ограниченный вес Хэмминга (
) имеют фиксированный или ограниченный вес Хэмминга (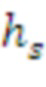
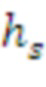 ).
).
Авторы изобретения обнаружили, к своему удивлению, что выбор границы маленькой имеет двойное преимущество: матричные произведения с матрицей закрытого ключа выполняются быстрее, и расстояние между необработанными ключами, вычисленными на каждой стороне, меньше (см. ниже). Последнее означает, что требуется меньше данных согласования и/или снижается вероятность отказа в протоколе и выработки узлами другого общего ключа.
В варианте реализации граница 
 равна 1 (
равна 1 (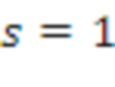
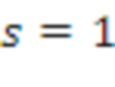 ). Т. е. элементы матрицы закрытого ключа имеют только коэффициенты со значениями -1, 0 и 1. Мы будет также называть это «двоичными числами со знаком».
). Т. е. элементы матрицы закрытого ключа имеют только коэффициенты со значениями -1, 0 и 1. Мы будет также называть это «двоичными числами со знаком».
Размеры матриц закрытого ключа выбирают так, чтобы их можно было умножать на матрицу 
 . Например, если
. Например, если 
 имеет размер
имеет размер 
 на
на 
 , то матрица закрытого ключа узла инициатора может быть матрицей размера
, то матрица закрытого ключа узла инициатора может быть матрицей размера 
 на
на 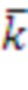
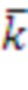 . Размер
. Размер 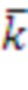
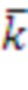 и
и 
 выбирают достаточно большим, чтобы получить достаточное количество битов в общем ключе и получить достаточно высокий уровень защиты.
выбирают достаточно большим, чтобы получить достаточное количество битов в общем ключе и получить достаточно высокий уровень защиты.
В дополнение к ограничению размера элементов матрицы закрытого ключа дальнейшие преимущества достигают путем ограничения количества ненулевых элементов. Мы будем называть весом Хэмминга столбца или строки матрицы сумму весом Хэмминга их компонентов. При этом вес Хэмминга многочлена определяют как количество ненулевых коэффициентов многочлена.
Авторы изобретения исследовали различные способы ограничения веса Хэмминга матриц закрытого ключа. Как правило, достаточно ограничить вес Хэмминга либо для столбцов, либо для строк в зависимости от того, умножают ли эту матрицу закрытого ключа на матрицу 
 слева или справа. Например, если матрицу закрытого ключа умножают на матрицу
слева или справа. Например, если матрицу закрытого ключа умножают на матрицу 
 справа (например,
справа (например, 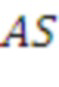
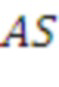 ), достаточно ограничить вес Хэмминга столбцов матрицы закрытого ключа.
), достаточно ограничить вес Хэмминга столбцов матрицы закрытого ключа.
Например, верхняя граница может быть выбрана для веса Хэмминга столбцов и/или строк матрицы закрытого ключа. Верхняя граница может быть одинаковой для всех столбцов и/или строк. В варианте реализации столбцы и/или строки матрицы закрытого ключа (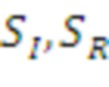
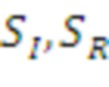 ) имеют одинаковый фиксированный вес Хэмминга.
) имеют одинаковый фиксированный вес Хэмминга.
Защита улучшается, если, в соответствии с условиями, матрицу закрытого ключа выбирают равномерным случайным образом из потенциально возможных матриц закрытого ключа, т. е. из матриц, которые удовлетворяют выбранным требованиям, например, в отношении границ для элементов и весов Хэмминга в столбцах или строках. Например, если требуется принудительно обеспечить условие, что вес Хэмминга каждого столбца равен 50, то матрицу закрытого ключа целесообразно выбирать из множества всех матриц правильных размеров, вес Хэмминга каждого столбца которых равен 50. Эффективные алгоритмы выбора равномерно случайной битовой строки с любым требуемым весом Хэмминга известны.
Другим способом ограничения веса Хэмминга матриц закрытого ключа является выбор столбцов и/или строк матрицы закрытого ключа (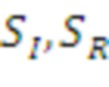
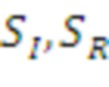 ) из вероятностного распределения. Например, элементы в матрице закрытого ключа (
) из вероятностного распределения. Например, элементы в матрице закрытого ключа (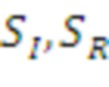
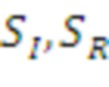 ) могут быть выбраны из неравного вероятностного распределения, где вероятность нулевого элемента выше вероятности ненулевого элемента. В варианте реализации вероятностное распределение выбирают так, что оно дает предварительно заданный ожидаемый вес Хэмминга для столбцов и /или строк. Например, чтобы выбрать столбец длины
) могут быть выбраны из неравного вероятностного распределения, где вероятность нулевого элемента выше вероятности ненулевого элемента. В варианте реализации вероятностное распределение выбирают так, что оно дает предварительно заданный ожидаемый вес Хэмминга для столбцов и /или строк. Например, чтобы выбрать столбец длины 
 и ожидаемого веса Хэмминга
и ожидаемого веса Хэмминга 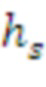
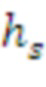 можно выбирать каждый элемент как ненулевой с вероятностью
можно выбирать каждый элемент как ненулевой с вероятностью 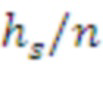
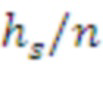 . Ненулевой элемент может быть выбран как 1 или -1, например, с равной вероятностью.
. Ненулевой элемент может быть выбран как 1 или -1, например, с равной вероятностью.
Узел-инициатор 110 содержит блок 150 матрицы открытого ключа. Узел-ответчик 210 содержит блок 250 матрицы открытого ключа. Блок матрицы открытого ключа вычисляет матрицу открытого ключа из матрицы 
 и матрицы
и матрицы 
 закрытого ключа.
закрытого ключа.
Термины «открытый» и «закрытый» призваны отражать ту мысль, что общий ключ не может быть получен только благодаря знанию открытой информации, или без знания некоторой закрытой информации. Но и требования по поводу активного обмена открытой информации нет. Например, протокол выработки общего ключа может быт выполнен посредством (предполагаемого) закрытого канала, который защищает открытые ключи от перехватчиков. В данном случае протокол выработки общего ключа обеспечивает дополнительный уровень защиты в случае взлома канала.
Блок матрицы открытого ключа вычисляет матрицу 
 открытого ключа (
открытого ключа (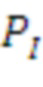
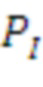 ,
, 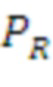
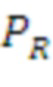 для инициатора и ответчика, соответственно) путем вычисления матричного произведения между общей матрицей (
для инициатора и ответчика, соответственно) путем вычисления матричного произведения между общей матрицей (
 ) и матрицей закрытого ключа (
) и матрицей закрытого ключа (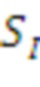
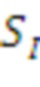 или
или 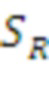
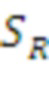 , соответственно) по первому модулю (
, соответственно) по первому модулю (
 ) и по модулю
) и по модулю 
 , получения произведения матриц и добавления шума.
, получения произведения матриц и добавления шума.
Обратите внимание, что это промежуточное произведение матриц не показывают. Знание общей матрицы 
 и результата этого перемножения матриц раскрыло бы закрытый ключ, т. к. он может быть вычислен путем инвертирования матрицы
и результата этого перемножения матриц раскрыло бы закрытый ключ, т. к. он может быть вычислен путем инвертирования матрицы 
 .
.
Добавление шума может быть выполнено путем выбора членов ошибок или членов шума и добавления их к элементу вышеупомянутого произведения матриц. Например, шум может быть выбран из гауссовского распределения с математическим ожиданием 0. Предпочтительным способом добавления шума является уменьшение масштаба произведения матриц, например, уменьшение масштаба коэффициентов.
В варианте реализации блок матрицы открытого ключа уменьшает произведение масштаб матриц до второго модуля 
 . Второй модуль p меньше первого модуля
. Второй модуль p меньше первого модуля 
 . Масштабированный элемент равен немасштабированному элементу, умноженному на второй модуль (
. Масштабированный элемент равен немасштабированному элементу, умноженному на второй модуль (
 ), деленному на первый модуль (
), деленному на первый модуль (
 ) и округленному до ближайшего целого числа. Например, если
) и округленному до ближайшего целого числа. Например, если 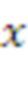
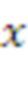 является немасштабированным элементом по модулю
является немасштабированным элементом по модулю 
 в произведении матриц, масштабированный элемент может быть выбран как
в произведении матриц, масштабированный элемент может быть выбран как 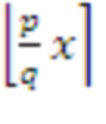
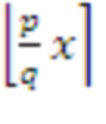 , где
, где 
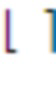 представляет ближайшее целое число. После операции масштабирования больше уже невозможно непосредственно вычислить закрытый ключ из открытого ключа и матрицы
представляет ближайшее целое число. После операции масштабирования больше уже невозможно непосредственно вычислить закрытый ключ из открытого ключа и матрицы 
 .
.
Элементы в матрице открытого ключа могут быть представлены как многочлены с коэффициентами в интервале 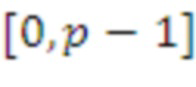
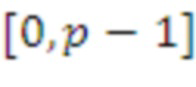 . Элементы в матрице закрытого ключа тоже могут быть представлены как многочлены с коэффициентами в интервале
. Элементы в матрице закрытого ключа тоже могут быть представлены как многочлены с коэффициентами в интервале 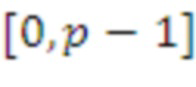
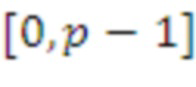 . Коэффициенты целесообразно выбирать в интервале
. Коэффициенты целесообразно выбирать в интервале 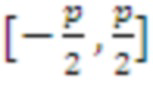
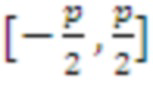 , чтобы уменьшать величину целых чисел для последующих умножений. Как указано выше, матрица закрытого ключа может также иметь коэффициенты, выбранные в интервале
, чтобы уменьшать величину целых чисел для последующих умножений. Как указано выше, матрица закрытого ключа может также иметь коэффициенты, выбранные в интервале 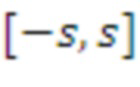
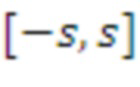 или даже
или даже 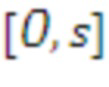
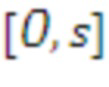 .
.
Умножение матрицы 
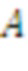 и матрицы
и матрицы 
 закрытого ключа выполняю по первому модулю
закрытого ключа выполняю по первому модулю 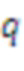
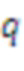 и
и 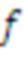
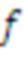 .Для этого сетевой узел может содержать блок приведения по модулю для приведения по модулю
.Для этого сетевой узел может содержать блок приведения по модулю для приведения по модулю 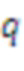
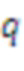 и модулю
и модулю 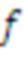
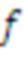 . Если коэффициенты в матрице
. Если коэффициенты в матрице 
 закрытого ключа маленькие, например, ограничены 1 или ограничены 1 по абсолютному значению, приведение по модулю может быть упрощено; во время умножения матриц всякий раза, когда коэффициент становится больше
закрытого ключа маленькие, например, ограничены 1 или ограничены 1 по абсолютному значению, приведение по модулю может быть упрощено; во время умножения матриц всякий раза, когда коэффициент становится больше 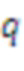
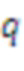 или меньше
или меньше 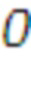
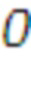 , результат возвращают обратно в интервал от 0 до
, результат возвращают обратно в интервал от 0 до 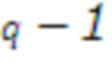
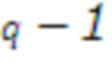 путем вычитания или прибавления
путем вычитания или прибавления 
 .
.
Как узел-инициатор, так и узел-ответчик отправляют свою матрицу открытого ключа другому узлу, например, используя интерфейсы 120 и 220 связи. Авторы изобретения обнаружили по меньшей мере три преимущества, которые реализуются за счет понижения масштаба произведения матриц. Прежде всего, исключается формирование и явное добавление шума в произведение матриц. Введение шума требует вычисления вероятностного распределения, например, гауссовского распределения. Оно относительно вычислительно затратное. Во-вторых, снижаются требования к связи. Т. к. второй модуль 
 меньше первого модуля
меньше первого модуля 
 , для представления элемента матрицы открытого ключа требуется меньше битов, чем в матрице закрытого ключа. В-третьих, извлечения, которые включают матрицу открытого ключа, меньше, т. к. они включают меньшие числа. Удивительно, что одна мера одновременно обеспечивает три преимущества.
, для представления элемента матрицы открытого ключа требуется меньше битов, чем в матрице закрытого ключа. В-третьих, извлечения, которые включают матрицу открытого ключа, меньше, т. к. они включают меньшие числа. Удивительно, что одна мера одновременно обеспечивает три преимущества.
Крайне предпочтительно, что второй модуль 
 делит первый модуль
делит первый модуль 
 . Что интересно, авторы изобретения обнаружили, что ни первый модуль, ни второй модуль не должны быть простым числом. Действительно, оказало, что выбор второго модуля (p) и/или первого модуля (q) в виде степени числа 2 обеспечивает преимущество, заключающееся в том, что открытый и закрытый ключи равномерно распределены. В варианте реализации как первый модуль, так и второй модуль являются степенью числа 2.
. Что интересно, авторы изобретения обнаружили, что ни первый модуль, ни второй модуль не должны быть простым числом. Действительно, оказало, что выбор второго модуля (p) и/или первого модуля (q) в виде степени числа 2 обеспечивает преимущество, заключающееся в том, что открытый и закрытый ключи равномерно распределены. В варианте реализации как первый модуль, так и второй модуль являются степенью числа 2.
В варианте реализации дополнительно требуется, чтобы 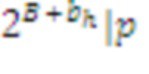
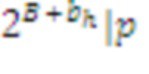 помимо того, что модули p и q являются степенью двойки. Эти приводит к равномерным общим ключам, даже если данные согласования наблюдаются.
помимо того, что модули p и q являются степенью двойки. Эти приводит к равномерным общим ключам, даже если данные согласования наблюдаются. 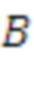
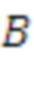 является количеством битов общего ключа на элемент необработанного ключа.
является количеством битов общего ключа на элемент необработанного ключа.
Величины модулей не должны быть слишком большими. Например, в варианте реализации второй модуль имеет размер в битах 12 или более и/или первый модуль имеет размер в битах 8 или более. В зависимости от требований к защите возможны большие или меньшие размеры. В варианте реализации 
 находится в диапазоне от 212 до 215,
находится в диапазоне от 212 до 215, 
 находится в диапазоне от 27 до 29 (включительно). Значения
находится в диапазоне от 27 до 29 (включительно). Значения 
 и
и 
 могут быть выбраны большими или меньшими в зависимости от требований безопасности.
могут быть выбраны большими или меньшими в зависимости от требований безопасности.
Узел-инициатор 110 содержит блок 160 общего ключа. Узел-ответчик 210 содержит блок 260 общего ключа. Блоки общего ключа отличаются в том смысле, что они либо формируют и передают, либо принимают и применяют данные согласования.
Как блок 160 общего ключа, так и блок 260 общего ключа выполнены с возможностью вычисления необработанного ключа 162, 262 в виде матричного произведения между принимаемой матрицей открытого ключа другого узла и матрицей закрытого ключа самого сетевого узла. Это произведение вычисляют по модулю многочлена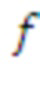
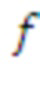 приведения. В случае использования масштабирования последнее вычисляют также по модулю второго модуля (
приведения. В случае использования масштабирования последнее вычисляют также по модулю второго модуля (
 ). Размеры матриц и произведений матриц выбирают так, что в случае опускания операции сканирования обе стороны вычисляли бы идентичный необработанный ключ. Т. е. в результате бы получались идентичные ключи без добавления шума, а все вычисления выполнялись бы по модулю q и
). Размеры матриц и произведений матриц выбирают так, что в случае опускания операции сканирования обе стороны вычисляли бы идентичный необработанный ключ. Т. е. в результате бы получались идентичные ключи без добавления шума, а все вычисления выполнялись бы по модулю q и 
 . Однако, из-за шума оба необработанных ключа не обязательно идентичные. Вычисление необработанного ключа может быть выполнено по модулю
. Однако, из-за шума оба необработанных ключа не обязательно идентичные. Вычисление необработанного ключа может быть выполнено по модулю 
 . Сетевые узлы могут содержать модульный блок для приведения результата умножение по модулю
. Сетевые узлы могут содержать модульный блок для приведения результата умножение по модулю 
 .
.
Блок 260 общего ключа узла-ответчика 210 выполнен с возможностью получения общего ключа 266 и получения данных 264 согласования из необработанного ключа 262 и отправки данных 264 согласования узлу-инициатору 110. На Фиг. 1 общий ключ получают из необработанного ключа и данных согласования, но это не обязательно, например, данные согласования могут быть также получены из необработанного ключа и общего ключа, например, если ответчик выполняет обмен ключами посредством инкапсуляции, например PST.CPA-KEM.Encapsulate или PST.NR.CCA-KEM.Encapsulate. Данные согласования могут принимать форму одного или более битов в необработанном ключа, например, битов из коэффициентов. Биты, выбираемые в качестве данных согласования, игнорируют при формировании ключа. В разделе «Литература» содержатся различные примеры данных согласования.
Блок 260 общего ключа выбирает некоторые биты из элементов необработанного ключа для формирования из них ключа. Например, выбранные биты могут быть конкатенированы. В варианте реализации выбранные биты вводят в функцию выработки производного ключа (KDF), например в криптографическую хэш-функцию. Пример KDF приведен, например, в CMLA_KDF из технической спецификации CMLA версии V1.43-20131218, или функция KDF определена в «Спецификации DRM », OMA-TS-DRM-DRM-V2_0_2-20080723-A, Open Mobile Alliance™, версия 2.0.2, раздел 7.1.2. Функция выработки производного ключа может быть применена к элементам битов ключа в необработанном ключе, например, полученным с помощью функции округления, например, после конкатенации, или из выходов функции согласования, например также после конкатенации.
Некоторые биты, которые выбирают в качестве битов ключа, могут быть выбраны в качестве данных согласования. Наконец, некоторые биты могут быть вообще отброшены. Данные согласования ключа, полученные из необработанного ключа блоком 260 общего ключа, отправляют узлу-инициатору 110.
Блок 160 общего ключа выполнен с возможностью приема данных 164 согласования (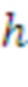
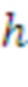 ) второго сетевого узла и вычисления общего ключа 166 путем применения функции согласования к принятым данным согласования и матрице 162 необработанного ключа. Например, функция согласования может быть применена к каждому из элементов в необработанном ключе 162 и соответствующей части данных согласования. Например, если данные 164 согласования были часть необработанного ключа, сформированного узлом-ответчиком 210, узел-инициатор может выбирать необработанный ключа, который мог быть получен узлом 210 и совместим с принятыми данными согласования, например, имеет те же самые средние биты, что и полученные.
) второго сетевого узла и вычисления общего ключа 166 путем применения функции согласования к принятым данным согласования и матрице 162 необработанного ключа. Например, функция согласования может быть применена к каждому из элементов в необработанном ключе 162 и соответствующей части данных согласования. Например, если данные 164 согласования были часть необработанного ключа, сформированного узлом-ответчиком 210, узел-инициатор может выбирать необработанный ключа, который мог быть получен узлом 210 и совместим с принятыми данными согласования, например, имеет те же самые средние биты, что и полученные.
Одну из матриц 
 и матрицы закрытого ключа можно использовать повторно для многократного выполнения протокола выработки общего ключа (если обе одни и те же, будет получен тот же самый общий ключ). Это уменьшит служебные данные обмена данными, особенно в случае повторного использования матрицы
и матрицы закрытого ключа можно использовать повторно для многократного выполнения протокола выработки общего ключа (если обе одни и те же, будет получен тот же самый общий ключ). Это уменьшит служебные данные обмена данными, особенно в случае повторного использования матрицы 
 . Однако авторы изобретения понимают, что в повторном использовании любой из матрицы
. Однако авторы изобретения понимают, что в повторном использовании любой из матрицы 
 и матрицы закрытого ключа нет необходимости, т. к. аутентификация не связана с этими элементами. В предпочтительном варианта реализации для каждого нового обмена ключами получают свежую матрицу
и матрицы закрытого ключа нет необходимости, т. к. аутентификация не связана с этими элементами. В предпочтительном варианта реализации для каждого нового обмена ключами получают свежую матрицу 
 и свежую матрицу закрытого ключа. Это дает преимущество, заключающееся в том, что злоумышленники не имеют возможности наблюдать дополнительную информацию путем наблюдения за несколькими исполнениями протокола. Кроме того, улучшается прямая секретность.
и свежую матрицу закрытого ключа. Это дает преимущество, заключающееся в том, что злоумышленники не имеют возможности наблюдать дополнительную информацию путем наблюдения за несколькими исполнениями протокола. Кроме того, улучшается прямая секретность.
После того, как протокол завершен и оба узла вычислили общий ключ, один из узлов может отправить сообщение о подтверждении ключа другому узлу для проверки того, что они выработали один и тот же общий ключ. Например, сообщение о подтверждении ключа может представлять собой хэш общего ключа, шифрование фиксированного значения, шифрование случайного значения вместе с этим фиксированным значением. Подтверждение ключа может быть также выполнено с использованием запросно-ответного протокола. Также можно пропустить подтверждение ключа. Если стороны получают разные общие ключи, последующий обмен данными между ними потерпит неудачу. Например, общий ключ может быть использован для шифрования и/или аутентификации дальнейших обменов данными, например для цифровых сообщений. Если они поступают при другом общем ключе, то расшифрование и/или верификация могут завершиться неудачей.
В различных вариантах реализации интерфейс связи может быть выбран из различных вариантов. Например, интерфейс связи может быть сетевым интерфейсом с локальной или глобальной вычислительной сетью, такой как Интернет, интерфейсом хранилища с внутренним или внешним хранилищем данных, клавиатурой и т. д.
Сетевые узлы могут содержать электронное запоминающее устройство, например, для хранения промежуточных данных, таких как матрица A, матрицы открытого и закрытого ключей, общий ключ и т. д. Запоминающее устройство может быть реализовано как электронная память, скажем, флэш-память, или магнитная память, скажем, жесткий диск и т. п. Запоминающее устройство может содержать множество дискретных памятей, вместе составляющих запоминающее устройство. Запоминающее устройство также может быть временной памятью, скажем, ОЗУ. В случае временного запоминающего устройства оно может использовать некоторые средства для получения общих параметров перед использованием, например, путем получения их по соединению оптической сети (не показано отдельно).
Как правило, каждое из устройств 110 и 210 содержит микропроцессор (не показан отдельно на Фиг. 1), который исполняет надлежащее программное обеспечение на устройствах 110 и 210; например, это программное обеспечение могло быть загружено и/или сохранено в соответствующей памяти, например, энергозависимой памяти, такой как ОЗУ, или энергонезависимой памяти, такой как флэш-память (не показана отдельно), В альтернативном варианте реализации устройства 110 и 210 полностью или частично реализованы в программируемой логике, например, такой как программируемая пользователем вентильная матрица (FPGA). Устройства 110 и 210 могут быть реализованы, полностью или частично, в виде так называемой специализированной интегральной схемы (ASIC), т. е. интегральной схемы (ИС), изготовленной на заказ для ее конкретного применения. Например, схемы могут быть реализованы в КМОП, например, с использованием языка описания аппаратных средств, такого как Verilog, VHDL и т. д.
В варианте реализации сетевой узел содержит схему интерфейса связи, схему общей матрицы, схему матрицы закрытого ключа, схему матрицы открытого ключа и схему общего ключа. Схемы реализуют соответствующие блоки, описанные в настоящем документе. Схемы могут быть схемой процессора и схемой запоминающего устройства, причем схема процессора исполняет инструкции, представленные в электронном виде в схемах запоминающего устройства.
Схема процессора может быть реализована распределенным образом, например, в виде нескольких схем подпроцессоров. Запоминающее устройство может быть распределенным по нескольким распределенным запоминающим подустройствам. Частично или полностью память может быть электронной памятью, магнитной памятью и т. д. Например, запоминающее устройством может иметь энергозависимую и энергонезависимую часть. Часть запоминающего устройства может быть предназначена только для чтения. Схемы могут также представлять собой FPGA, ASIC и т. п.
На Фиг. 2 схематически показан пример варианта реализации способа 400 электронного обмена ключами. Способ может быть исполнен первым узлом электронной сети, таким как узел-инициатор 110 или узел-ответчик 210.
Способ 400 включает:
- осуществление (410) цифровой связи между первым сетевым узлом и вторым сетевым узлом,
- прием (415) в качестве входа параметра сложности (
 ) и параметра структуры (
) и параметра структуры (
 ),
),
- получение (420) общей матрицы (
 ), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
 ) представляет собой квадратную матрицу (
) представляет собой квадратную матрицу (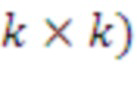
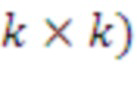 размера (
размера (
 ), равного параметру (
), равного параметру (
 ) сложности, деленному на параметр (
) сложности, деленному на параметр (
 ) структуры, элементы в общей матрице (
) структуры, элементы в общей матрице (
 ) представляют собой целочисленные многочлены степени меньше параметра (n) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
) представляют собой целочисленные многочлены степени меньше параметра (n) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирование (430) матрицы (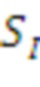
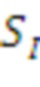 ) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирование (440) матрицы (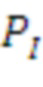
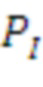 ) открытого ключа путем
) открытого ключа путем
- вычисления (442) матричного произведения между общей матрицей (
 ) и матрицей (
) и матрицей (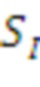
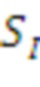 ) закрытого ключа по модулю первого модуля (
) закрытого ключа по модулю первого модуля (
 ) и по модулю многочлена (
) и по модулю многочлена (
 ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления (444) шума к элементам в произведении матриц,
) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления (444) шума к элементам в произведении матриц,
- отправку (452) матрицы общего ключа первого сетевого узла второму сетевому узлу,
- прием (454) матрицы (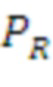
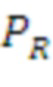 ) открытого ключа второго сетевого узла,
) открытого ключа второго сетевого узла,
- вычисление (460) необработанного ключа как матричного произведения между принятой матрицей открытого ключа второго узла и матрицей закрытого ключа первого сетевого узла.
Если первый сетевой узел функционирует, например, в соответствии с режимом инициатора в протоколе обмена ключами, то первый сетевой узел выполняет следующий дальнейшие этапы:
- прием (472) данных (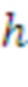
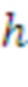 ) согласования второго сетевого узла,
) согласования второго сетевого узла,
- вычисление (482) общего ключа или сообщения путем применения функции (
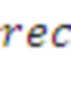 ) согласования к принятым данным согласования и необработанному ключу.
) согласования к принятым данным согласования и необработанному ключу.
Если первый сетевой узел функционирует, например, в соответствии с режимом ответчика в протоколе обмена ключами, то первый сетевой узел выполняет следующий дальнейшие этапы:
- получение (474) общего ключа и получение данных согласования из необработанного ключа,
- отправку (484) данных согласования второму сетевому узлу.
Как очевидно специалисту в данной области, возможны множество разных путей исполнения способа. Например, порядок этапов может быть изменен или некоторые этапы могут быть исполнены параллельно. Кроме того, между этапами могут быть вставлены другие этапы способа. Вставленные этапы могут представлять собой усовершенствования способа, такие как описанные в настоящем документе, или могут не иметь отношения к способу. Например, данный этап может быть не завершен полностью до начала следующего этапа.
Способ согласно настоящему изобретению может быть исполнен с использованием программного обеспечения, которое содержит инструкции для вызова выполнения процессорной системой способа 400. Программное обеспечение может содержать только те этапы, которые предпринимаются компонентом системы. Программное обеспечение может храниться в подходящем носителе информации, таком как жесткий диск, гибкий диск, память, оптический диск и т. д. Программное обеспечение может быть отправлено в виде сигнала по проводу или без провода либо с использованием сети данных, например Интернета. Программное обеспечение может быть доступно для загрузки и/или удаленного использования на сервере. Способ согласно настоящему изобретению может быть исполнен с использованием битового потока, выполненного с возможностью конфигурирования программируемой логики, например, программируемой пользователем вентильной матрицы (FPGA), для осуществления способа.
Понятно, что изобретение также распространяется на компьютерные программы, в частности, на компьютерные программы на или в носителе, приспособленном для воплощения изобретения на практике. Программа может быть в виде исходного кода, объектного кода, промежуточного источника кода и объектного кода, например, в частично компилированном виде или любом ином виде, пригодном для использования в реализации способа согласно настоящему изобретению. Вариант реализации, относящийся к компьютерному программному продукту, содержит выполненные с возможность исполнения инструкции, соответствующие каждому из этапов обработки по меньшей мере одного из изложенных способов. Эти инструкции могут подразделяться на подпрограммы и/или храниться в одном или более файлов, которые могут быть связаны статически или динамически. Другой вариант реализации, относящийся к компьютерному программному продукту, содержит выполненные с возможность исполнения инструкции, соответствующие каждому из средству по меньшей мере одной из описанных систем и/или продуктов.
На Фиг. 3a показан компьютерочитаемый носитель 1000 информации, имеющий часть 1010, содержащую компьютерную программу 1020, причем компьютерная программа 1020 содержит инструкции для вызова выполнения процессорной системой способа выработки общего ключа согласно настоящему изобретению. Компьютерная программа 1020 может быть реализована на компьютерочитаемом носителе 1000 информации в виде физических меток или посредством намагничивания компьютерочитаемого носителя 1000 информации. Однако возможен и любой другой подходящий вариант реализации. Кроме того, понятно, что хотя компьютерочитаемый носитель 1000 информации показан здесь в виде оптического диска, компьютерочитаемый носитель 1000 информации может быть любым подходящим компьютерочитаемым носителем информации, таким как жесткий диск, твердотельной памятью, флэш-памятью и т. д,, и может быть выполнен без возможности записи или с возможностью записи. Компьютерная программа 1020 содержит инструкции для вызова выполнения процессорной системой способа 400 выработки общего ключа или других криптографических операций согласно настоящему изобретению.
На Фиг. 3b показано схематическое представление процессорной системы 1140 согласно настоящему изобретению, например, для реализации одной или более криптографических операций. Процессорная система содержит одну или более интегральных схем 1110. Архитектура одной или более интегральных схем 1110 схематически показана на Фиг. 3b. Схема 1110 содержит блок 1120 обработки, например, ЦП, для выполнения компонентов компьютерной программы с целью осуществления способа согласно варианту реализации и/или реализации его модулей или блоков. Схема 1110 содержит память 1122 для хранения программного кода, данных и т. д. Часть памяти 1122 может быть предназначена только для чтения. Схема 1110 может содержать элемент 1126 связи, например, антенну, разъемы или то и другое и т. п. Схема 1110 может содержать специализированную интегральную схему 1124 для выполнения части или всей обработки, определенной в способе. Процессор 1120, память 1122, специализированная ИС 1124 и элемент 1126 связи могут быть соединены друг с другом посредством межсоединения 1130, скажем, шины. Процессорная система 1110 может быть выполнена с возможностью контактного и бесконтактного обмена данными с использованием антенны и/или разъемов, соответственно.
Например, в варианте реализации сетевой узел может содержать схему процессора и схему памяти, причем процессор выполнен с возможностью исполнения программного обеспечения, хранящегося в схеме памяти. Например, схема процессора может представлять собой процессор Intel Core i7, ARM Cortex-R8 и т. д. В варианте реализации схема процессора может представлять собой ARM Cortex M0. Схема памяти может быть схемой ПЗУ или энергонезависимой памяти, например, флэш-памяти. Схема памяти может быть схемой энергозависимой памяти, например, СОЗУ. В последнем случае устройство проверки подлинности может содержать энергонезависимый программный интерфейс, например, жесткий диск, сетевой интерфейс и т. д., выполненные с возможностью снабжения программным обеспечением.
На Фиг. 4a схематически показан пример варианта реализации узла 310 расшифрования с открытым ключом. Эта фигура содержит параметры 331 сложности и структуры, интерфейс 320 связи, блок 340 закрытого ключа, блок 360 вычисления сообщения, необработанный ключ 362, вторую часть 364 шифртекста и сообщение 366. Эти блоки могут функционировать в соответствии с алгоритмом PST.NR.CPA-PKE.Decrypt(), приведенным выше, например, блок 340 закрытого ключа может получать S, а блок 360 вычисления сообщения может вычислять 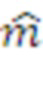
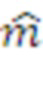 . Обратите внимание, что эта фигура аналогична сетевому узлу 110 типа инициатора, показанному на Фиг. 1, за исключением того, что показаны компоненты, которые соответствуют операции расшифрования открытого ключа. В частности, как показано в алгоритмах PST.CPA-KEM и PST.NR.CCA-KEM, сетевой узел 110 может выполнять обмен ключами с использованием алгоритмов формирования открытого ключа, например, PST.NR.CPA-PKE.Keygeneration(), и алгоритмов расшифрования открытого ключа, например PST.NR.CPA-PKE.Decrypt(). На Фиг. 1 в этом расшифровании участвуют параметры 131 сложности и структуры, интерфейс 120 связи, блок 140 закрытого ключа, блок 160 общего ключа, необработанный ключ 162, данные 164 согласования и общий ключ 166. На Фиг. 4a показан сетевой узел с открытым ключом, который выполняет расшифрования без обязательного выполнения также формирования ключа, следовательно, он имеет только те элементы с Фиг. 1, которые относятся к расшифрованию. Т. е. элемент 331 может соответствовать элементу 131; элемент 320 может соответствовать элементу 120; элемент 340 может соответствовать элементу 140; элемент 360 может соответствовать элементу 160; элемент 362 может соответствовать элементу 162; элемент 364 может соответствовать элементу 164; и элемент 366 может соответствовать элементу 166. Обратите внимание, что узел 310 расшифрования открытого ключа получает сообщение 366 в результате расшифрования, тогда как сетевой узел 110 получает общий ключ 166; однако операции для получения этих соответствующих результатов могут быть в действительности одними и теми же в обоих случаях.
. Обратите внимание, что эта фигура аналогична сетевому узлу 110 типа инициатора, показанному на Фиг. 1, за исключением того, что показаны компоненты, которые соответствуют операции расшифрования открытого ключа. В частности, как показано в алгоритмах PST.CPA-KEM и PST.NR.CCA-KEM, сетевой узел 110 может выполнять обмен ключами с использованием алгоритмов формирования открытого ключа, например, PST.NR.CPA-PKE.Keygeneration(), и алгоритмов расшифрования открытого ключа, например PST.NR.CPA-PKE.Decrypt(). На Фиг. 1 в этом расшифровании участвуют параметры 131 сложности и структуры, интерфейс 120 связи, блок 140 закрытого ключа, блок 160 общего ключа, необработанный ключ 162, данные 164 согласования и общий ключ 166. На Фиг. 4a показан сетевой узел с открытым ключом, который выполняет расшифрования без обязательного выполнения также формирования ключа, следовательно, он имеет только те элементы с Фиг. 1, которые относятся к расшифрованию. Т. е. элемент 331 может соответствовать элементу 131; элемент 320 может соответствовать элементу 120; элемент 340 может соответствовать элементу 140; элемент 360 может соответствовать элементу 160; элемент 362 может соответствовать элементу 162; элемент 364 может соответствовать элементу 164; и элемент 366 может соответствовать элементу 166. Обратите внимание, что узел 310 расшифрования открытого ключа получает сообщение 366 в результате расшифрования, тогда как сетевой узел 110 получает общий ключ 166; однако операции для получения этих соответствующих результатов могут быть в действительности одними и теми же в обоих случаях.
На Фиг. 4b схематически показан пример варианта реализации узла 510 с шифрованием с открытого ключа. Данная фигура содержит параметры 531 сложности и структуры; блок 530 общей матрицы; интерфейс 520 связи; блок 540 закрытой матрицы; блок 550 первой части шифртекста; блок 560 второй части шифртекста; необработанный ключ 562; сообщение 566; и вторую часть 564 шифртекста. Узел 510 шифрования принимает в качестве входа параметры 531 сложности и структуры; получает общую матрицу 530; формирует с помощью блока 540 закрытой матрицы закрытую матрицу; формирует с помощью блока 550 первой части шифртекста первую часть шифртекста; и формирует с помощью блока 560 второй части шифртекста вторую часть 564 шифртекста, причем последнюю вычисляет из необработанного ключа 562 и сообщения 566. Например, эти блоки могут функционировать в соответствии с одним из алгоритмов PST.NR.CPA-PKE.Encryptwithrho, PST.NR.CPA-PKE.Encrypt, PST.CPA-PKE.Encryptwithrho или PST.CPA-PKE.Encrypt, как подробно описано выше. Например, блок 530 общей матрицы может получать A, блок 540 закрытой матрицы может формировать R, блок 550 первой части шифртекста может формировать U и блок 560 второй части шифртекста может вычислять v. Эта фигура аналогична сетевому узлу 210 типа ответчика, показанному на Фиг. 1; в частности, как показано в PST.CPA-KEM и PST.NR.CCA-KEM, узел-ответчик при обмене ключами или инкапсуляции ключа может, в действительности, выполнять шифрование открытого ключа, например, выполняемое узлом 510 с шифрованием открытого ключа.
Следующие пункты не являются формулой изобретения, а содержат предлагаемые варианты реализации. Заявитель настоящим уведомляет о том, что к таким пунктам и/или сочетаниям таких пунктов и/или признаков, взятых из описания или формулы изобретения, могут быть сформулированы новые пункты во время судебного процесса по настоящей заявке или по любой дальнейшей заявке, полученной из нее.
1. Первый узел (110) электронной сети, выполненный с возможностью осуществления криптографической операции, содержащий:
- интерфейс (120) связи, выполненный с возможностью осуществления цифровой связи со вторым сетевым узлом,
- схему процессора, выполненную с возможностью:
- приема в качестве входа параметра (
 ) сложности и параметра (
) сложности и параметра (
 ) структуры,
) структуры,
- получения общей матрицы (
 ), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
 ) представляет собой квадратную матрицу (
) представляет собой квадратную матрицу (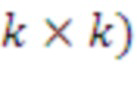
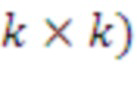 размера (
размера (
 ), равного параметру (
), равного параметру (
 ) сложности, деленному на параметр (
) сложности, деленному на параметр (
 ) структуры, элементы в общей матрице (
) структуры, элементы в общей матрице (
 ) представляют собой целочисленные многочлены степени меньше параметра (
) представляют собой целочисленные многочлены степени меньше параметра (
 ) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирования матрицы (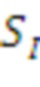
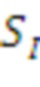 ) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирования матрицы (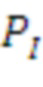
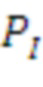 ) открытого ключа путем
) открытого ключа путем
- вычисления матричного произведения между общей матрицей (
 ) и матрицей (
) и матрицей (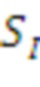
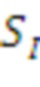 ) закрытого ключа по модулю первого модуля (
) закрытого ключа по модулю первого модуля (
 ) и по модулю многочлена (
) и по модулю многочлена (
 ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, и
) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, и
- отправки матрицы открытого ключа первого сетевого узла второму сетевому узлу.
2. Первый узел (110) электронной сети по пункту 1, в котором криптографическая операция представляет собой протокол обмена ключами (KEX), причем процессор выполнен с возможностью:
- приема матрицы (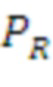
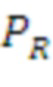 ) открытого ключа второго сетевого узла,
) открытого ключа второго сетевого узла,
- вычисления необработанного ключа как матричного произведения между принятым открытым ключом второго узла и матрицей закрытого ключа первого сетевого узла,
при этом первый сетевой узел также выполнен с возможностью:
- приема данных (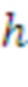
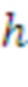 ) согласования второго сетевого узла,
) согласования второго сетевого узла,
- вычисления общего ключа путем применения функции (
 ) согласования к принятым данным согласования и необработанному ключу, или
) согласования к принятым данным согласования и необработанному ключу, или
при этом первый сетевой узел также выполнен с возможностью:
- получения общего ключа и данных согласования из необработанного ключа,
- отправки данных согласования второму сетевому узлу.
3. Первый сетевой узел по любому из предыдущих пунктов, в котором криптографическая операция является одной из следующих: протокол обмена ключами (KEX), метод инкапсуляции ключа (KEM), шифрование открытого ключа (PKE), цифровая подпись.
4. Первый сетевой узел по любому из предыдущих пунктов, в котором многочлен приведения представляет собой 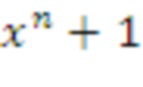
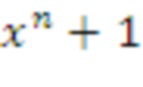 , или
, или 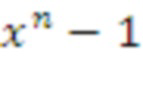
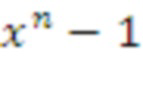 , или
, или 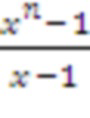
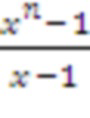 .
.
5. Первый сетевой узел по любому из предыдущих пунктов, в котором:
- параметр (
 ) структуры делит параметр (
) структуры делит параметр (
 ) сложности,
) сложности,
- размер общей матрицы (
 ) получают путем округления параметра (
) получают путем округления параметра (
 ) сложности, деленного на параметр (
) сложности, деленного на параметр (
 ) структуры, например, округления до ближайшего целого числа, округления вверх или округления вниз.
) структуры, например, округления до ближайшего целого числа, округления вверх или округления вниз.
6. Первый сетевой узел по любому из предыдущих пунктов, в котором:
- параметр (
 ) структуры является целым числом, которое не меньше 1 и не больше параметра (
) структуры является целым числом, которое не меньше 1 и не больше параметра (
 ;
; 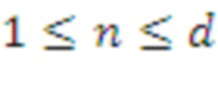
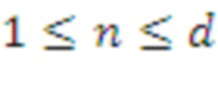 ) сложности, и/или
) сложности, и/или
- параметр (
 ) структуры ограничен тем, что он является простым числом, и/или
) структуры ограничен тем, что он является простым числом, и/или
- параметр (
 ) является степенью числа 2, а первый модуль является простым числом, и/или
) является степенью числа 2, а первый модуль является простым числом, и/или
- параметр (
 ) ограничен тем, что он является простым числом, а первый модуль является простым числом, и/или
) ограничен тем, что он является простым числом, а первый модуль является простым числом, и/или
- параметр (
 ) ограничен тем, что он является простым числом, а первый модуль является степенью двойки, и/или
) ограничен тем, что он является простым числом, а первый модуль является степенью двойки, и/или
- параметр (
 ) структуры ограничен тем, что он является простым числом, а первый модуль является степенью двойки и многочлен приведения неприводим по модулю 2.
) структуры ограничен тем, что он является простым числом, а первый модуль является степенью двойки и многочлен приведения неприводим по модулю 2.
7. Первый сетевой узел по любому из предыдущих пунктов, в котором схема процессора выполнена с возможностью вычисления расширенной общей матрицы для общей матрицы (A) путем замены элементов-многочленов степени больше 0 циркулянтной матрицей, причем указанная расширенная матрица имеет количество столбцов и строк, равное параметру сложности.
8. Первый сетевой узел по пункту 7, в котором схема процессора выполнена с возможностью вычисления расширенной общей матрицы для общей матрицы (A), содержащей d × d элементов, причем каждый элемент является целым числом, а ту же самую схему процессора используют для оценки этой общей матрицы (A) и для получения открытого ключа, причем параметр (
 ) структуры является единицей (1) или равен параметру (
) структуры является единицей (1) или равен параметру (
 ) сложности.
) сложности.
9. Первый сетевой узел по любому из предыдущих пунктов, в котором криптографическая операция представляет собой шифрование открытого ключа, и в котором общая матрица и матрица открытого ключа являются открытым ключом, и в котором матрица закрытого ключа является закрытым ключом.
10. Первый сетевой узел по любому из предыдущих пунктов, в котором добавление шума к произведению матриц включает:
- уменьшение масштаба элементов произведения матриц до второго модуля (
 ), причем масштабированный элемент равен немасштабированному элементу, умноженному на второй модуль (
), причем масштабированный элемент равен немасштабированному элементу, умноженному на второй модуль (
 ), деленному на первый модуль (
), деленному на первый модуль (
 ) и округленному до ближайшего целого числа, второй модуль (
) и округленному до ближайшего целого числа, второй модуль (
 ) меньше первого модуля (
) меньше первого модуля (
 ), граница (
), граница (
 ) не превышает второй модуль (
) не превышает второй модуль (
 ), при этом вычисление необработанного ключа в виде матричного произведения между принятым открытым ключом второго узла и матрицей закрытого ключа первого сетевого узла выполняют по модулю второго модуля (
), при этом вычисление необработанного ключа в виде матричного произведения между принятым открытым ключом второго узла и матрицей закрытого ключа первого сетевого узла выполняют по модулю второго модуля (
 ),
),
или
- выбор элементов шума для одного или более или всех элементов в произведении матриц из распределения шума и добавление элементов шума к одному или более или всех элементам в произведении матрицы, например, когда элементы шума имеют коэффициенты, выбранные из гауссовского распределения с математическим ожиданием 0.
11. Первый сетевой узел по любому из предыдущих пунктов, в котором:
- матрицу закрытого ключа (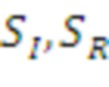
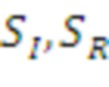 ) выбирают равномерным случайным образом потенциально возможных матриц закрытого ключа, и/или
) выбирают равномерным случайным образом потенциально возможных матриц закрытого ключа, и/или
- коэффициенты элементов в матрице закрытого ключа ограничивают по абсолютному значению посредством границы (границы), например, когда упомянутая граница равна 2 (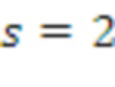
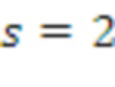 ), или когда граница равна 1 (
), или когда граница равна 1 (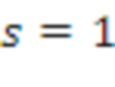
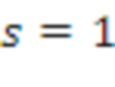 ), причем последний случай соответствует двоичным числам со знаком, и/или
), причем последний случай соответствует двоичным числам со знаком, и/или
- столбцы и/или строки закрытого ключа (
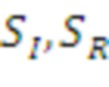 ) имеют фиксированный или ограниченный вес Хэмминга (
) имеют фиксированный или ограниченный вес Хэмминга (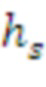
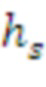 ).
).
12. Первый сетевой узел по любом из предыдущих пунктов, в котором элементы в матрице закрытого ключа (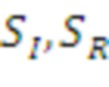
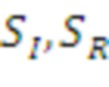 ) выбирают из неравного вероятностного распределения, где вероятность нулевого элемента выше вероятности ненулевого элемента.
) выбирают из неравного вероятностного распределения, где вероятность нулевого элемента выше вероятности ненулевого элемента.
13. Первый сетевой узел по любому из предыдущих пунктов, выполненный с возможностью получения другой матрицы (
 ) и/или другого закрытого ключа для каждого нового обмена ключами.
) и/или другого закрытого ключа для каждого нового обмена ключами.
14. Первый сетевой узел по любому из предыдущих пунктов, выполненный с возможностью получения общей матрицы (
 ) путем формирования случайного начального числа и отправки случайного начального числа посредством канала связи другому узлу, причем первый и второй сетевые узлы используют случайное начальное число для затравки детерминированного генератора псевдослучайных чисел, формируя матрицу (
) путем формирования случайного начального числа и отправки случайного начального числа посредством канала связи другому узлу, причем первый и второй сетевые узлы используют случайное начальное число для затравки детерминированного генератора псевдослучайных чисел, формируя матрицу (
 ) из выхода генератора псевдослучайных чисел.
) из выхода генератора псевдослучайных чисел.
16. Способ (400) электронной криптографической операции для первого узла (110) электронной сети, включающий:
- осуществление (410) цифровой связи между первым сетевым узлом и вторым сетевым узлом,
- прием (415) в качестве входа параметра (
 ) сложности и параметра (
) сложности и параметра (
 ) структуры,
) структуры,
- получение (420) общей матрицы (
 ), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
 ) представляет собой квадратную матрицу (
) представляет собой квадратную матрицу (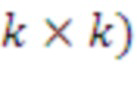
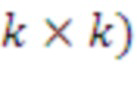 размера (
размера (
 ), равного параметру (
), равного параметру (
 ) сложности, деленному на параметр (
) сложности, деленному на параметр (
 ) структуры, элементы в общей матрице (
) структуры, элементы в общей матрице (
 ) представляют собой целочисленые многочлены степени меньше параметра (
) представляют собой целочисленые многочлены степени меньше параметра (
 ) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирование (430) матрицы (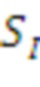
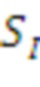 ) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирование (440) матрицы (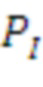
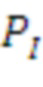 ) открытого ключа путем
) открытого ключа путем
- вычисления (442) матричного произведения между общей матрицей (
 ) и матрицей (
) и матрицей (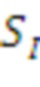
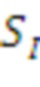 ) закрытого ключа по модулю первого модуля (
) закрытого ключа по модулю первого модуля (
 ) и по модулю многочлена (
) и по модулю многочлена (
 ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления (444) шума к элементам в произведении матриц,
) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления (444) шума к элементам в произведении матриц,
- отправку (452) матрицы общего ключа первого сетевого узла второму сетевому узлу.
Согласно аспекту настоящего изобретения предложен первый узел электронной сети, выполненный с возможностью осуществления криптографической операции, содержащий:
- интерфейс связи, выполненный с возможностью осуществления цифровой связи со вторым сетевым узлом,
- схему процессора, выполненную с возможностью:
- приема в качестве входа параметра (
 ) сложности и параметра (
) сложности и параметра (
 ) структуры,
) структуры,
- получения общей матрицы (
 ), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (
 ) представляет собой квадратную матрицу (
) представляет собой квадратную матрицу (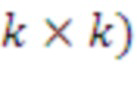
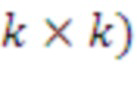 размера (
размера (
 ), равного параметру (
), равного параметру (
 ) сложности, деленному на параметр (
) сложности, деленному на параметр (
 ) структуры, элементы в общей матрице (
) структуры, элементы в общей матрице (
 ) представляют собой целочисленные многочлены степени меньше параметра (
) представляют собой целочисленные многочлены степени меньше параметра (
 ) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирования закрытой матрицы (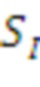
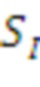 ), причем элементы в закрытой матрице представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
), причем элементы в закрытой матрице представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирования открытой матрицы (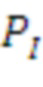
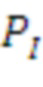 ) первого сетевого узла путем:
) первого сетевого узла путем:
- вычисления матричного произведения между общей матрицей (
 ) и закрытой матрицей (
) и закрытой матрицей (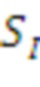
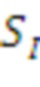 ) по модулю первого модуля (
) по модулю первого модуля (
 ) и по модулю многочлена (
) и по модулю многочлена (
 ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, и
) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, и
- отправки общей матрицы первого сетевого узла второму сетевому узлу.
Такая схема процессора может быть также выполнена с возможностью:
- приема открытой матрицы (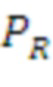
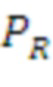 ) второго сетевого узла,
) второго сетевого узла,
- вычисления необработанного ключа как матричного произведения между принятой открытой матрицей второго узла и закрытой матрицей первого сетевого узла,
при этом первый сетевой узел также выполнен с возможностью:
- приема криптографического материала второго сетевого узла,
- вычисления общих данных между первым сетевым узлом и вторым сетевым узлом из принятого криптографического материала и необработанного ключа, или
при этом первый сетевой узел также выполнен с возможностью:
- получения общих данных между первым сетевым узлом и вторым сетевым узлом и получения криптографического материала из необработанного ключа,
- отправки криптографического материала второму сетевому узлу.
Например, закрытая матрица может быть матрицей закрытого ключа, например, в том случае, когда криптографическая операция представляет собой обмен ключами или механизм инкапсуляции ключа. Одна или более из открытой матрицы первого сетевого узла и открытой матрицы второго сетевого узла могут быть матрицей открытого ключа, например, в том случае, когда криптографическая операция представляет собой обмен ключами, механизм инкапсуляции ключа или шифрование открытого ключа. Общие данные могут быть общим ключом или данными, из которых выводят общий ключ, например, в том случае, когда криптографическая операция представляет собой обмен ключами или механизм инкапсуляции ключа; или сообщением, например, в том случае. когда криптографическая операция представляет собой шифрование открытого ключа. Криптографический материал может быть данными согласования, например, в том случае, когда криптографическая операция представляет собой обмен ключами ил механизм инкапсуляции ключа, или он может быть частью шифртекста, например, в том случае, когда криптографическая операция представляет собой шифрование открытого ключа, или обмен ключами, или инкапсуляцию ключа на основе шифрования открытого ключа.
Следует отметить, что вышеупомянутые варианты реализации иллюстрируют, а не ограничивают, настоящее изобретение, и что специалисты в данной области техники в состоянии разработать множество альтернативных вариантов реализации.
В формуле изобретения любые номера позиций, указанные в скобках, не следует трактовать как ограничивающие пункт формулы изобретения. Использование глагола «содержит/включает в себя» и его спряжений не исключает наличия других элементов или этапов, кроме указанных в пункте формулы изобретения. Грамматические средства выражения единственного числа, используемые с элементом, не исключает наличия множества таких элементов. Настоящее изобретение может быть реализовано посредством оборудования, содержащего несколько различных элементов, и посредством соответствующим образом запрограммированного компьютера. В описывающем устройство пункте, перечисляющем несколько средств, некоторые из этих средств могут быть реализованы одним и тем же элементом оборудования. Сам факт того, что определенные меры изложены во взаимно отличающихся зависимых пунктах формулы, не означает того, комбинация этих мер не может быть использована эффективно.
В формуле изобретения ссылки в скобках относятся к номерам позиций на чертежах, демонстрирующих примеры вариантов реализации, или к формулам в вариантов реализации, тем самым повышая понятность пункта формулы изобретения. Эти ссылке не должны толковаться как ограничивающие пункт формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПРОТОКОЛЫ ИНКАПСУЛЯЦИИ КЛЮЧЕЙ | 2019 |
|
RU2787692C2 |
| УСТРОЙСТВА И СПОСОБ СОГЛАСОВАНИЯ КЛЮЧЕЙ | 2018 |
|
RU2736109C1 |
| УСТРОЙСТВА И СПОСОБ ОБМЕНА КЛЮЧАМИ | 2018 |
|
RU2737105C1 |
| УСТРОЙСТВО И СПОСОБ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ МАТРИЦЫ ДЛЯ ИСПОЛЬЗОВАНИЯ В КРИПТОГРАФИЧЕСКОМ ПРОТОКОЛЕ | 2018 |
|
RU2765238C2 |
| Повышение неоднозначности | 2016 |
|
RU2737917C1 |
| СПОСОБ ШИФРОВАНИЯ БЛОКА ДАННЫХ, ПРЕДСТАВЛЕННОГО В ВИДЕ БИТОВОЙ СТРОКИ | 2014 |
|
RU2542929C1 |
| СПОСОБ СИММЕТРИЧНОГО ШИФРОВАНИЯ НА ОСНОВЕ СМЕШАННОЙ СИСТЕМЫ СЧИСЛЕНИЯ | 2009 |
|
RU2429575C2 |
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ И ДОСТУПНОСТИ ИНФОРМАЦИИ В РАСПРЕДЕЛЕННЫХ СИСТЕМАХ ХРАНЕНИЯ ДАННЫХ | 2023 |
|
RU2812948C1 |
| Способ шифрования информации и устройство для осуществления способа | 2020 |
|
RU2756976C1 |
| СПОСОБ И УСТРОЙСТВО ФОРМИРОВАНИЯ МНОГОЗНАЧНЫХ КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ ЗАЩИЩЕННОЙ ПЕРЕДАЧИ ДАННЫХ ПО КАНАЛАМ СВЯЗИ | 2023 |
|
RU2815193C1 |
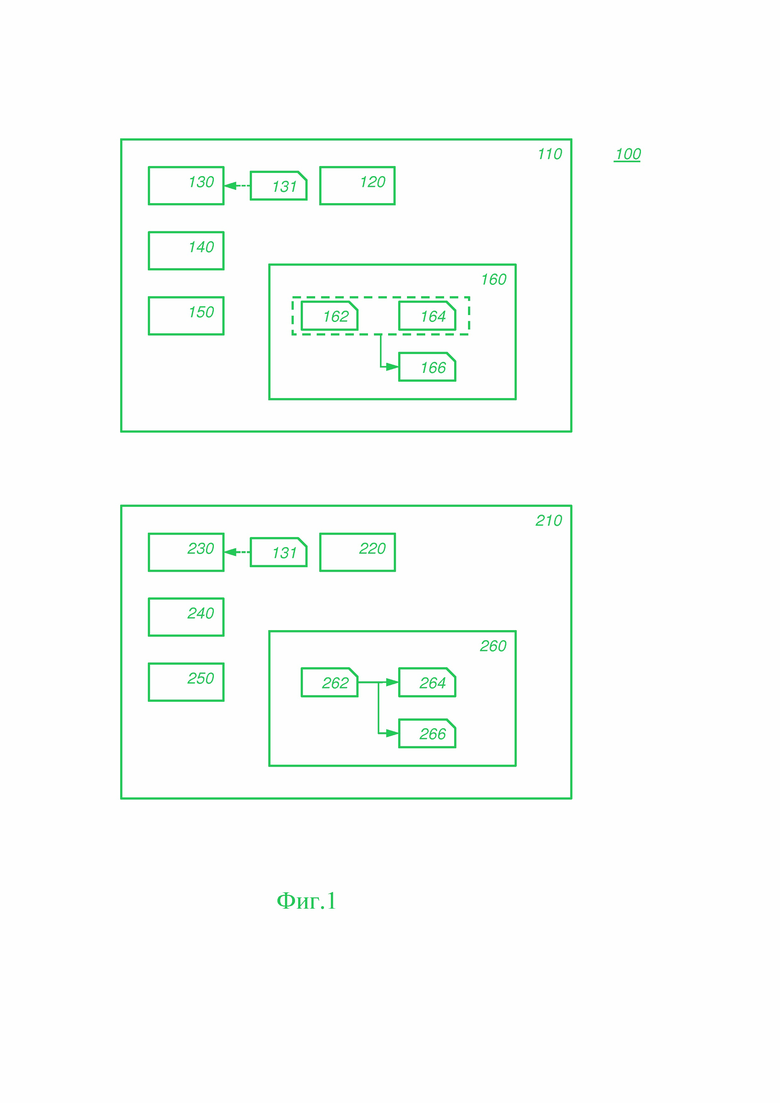
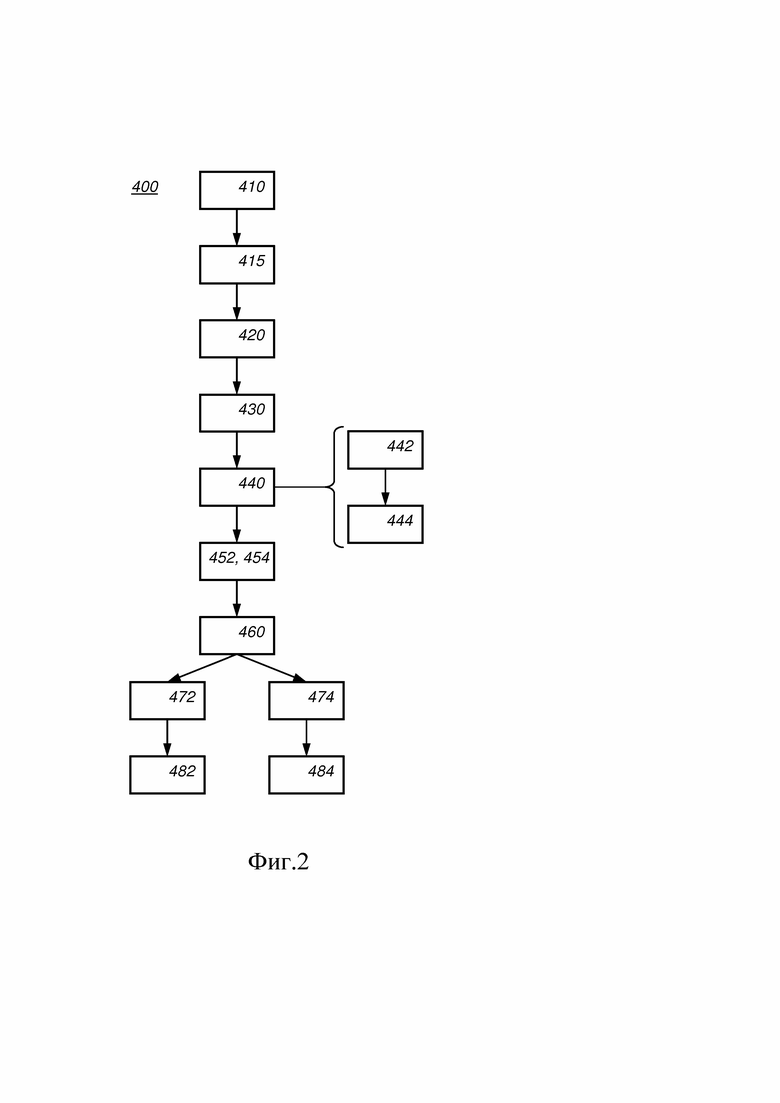
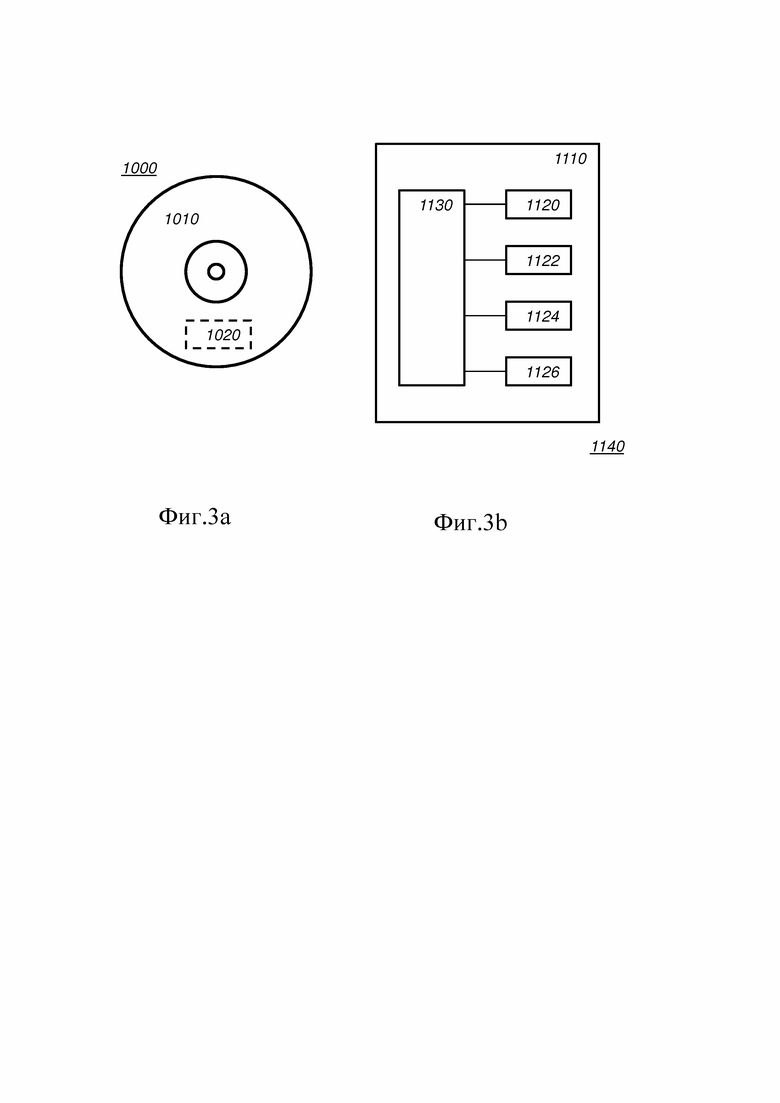
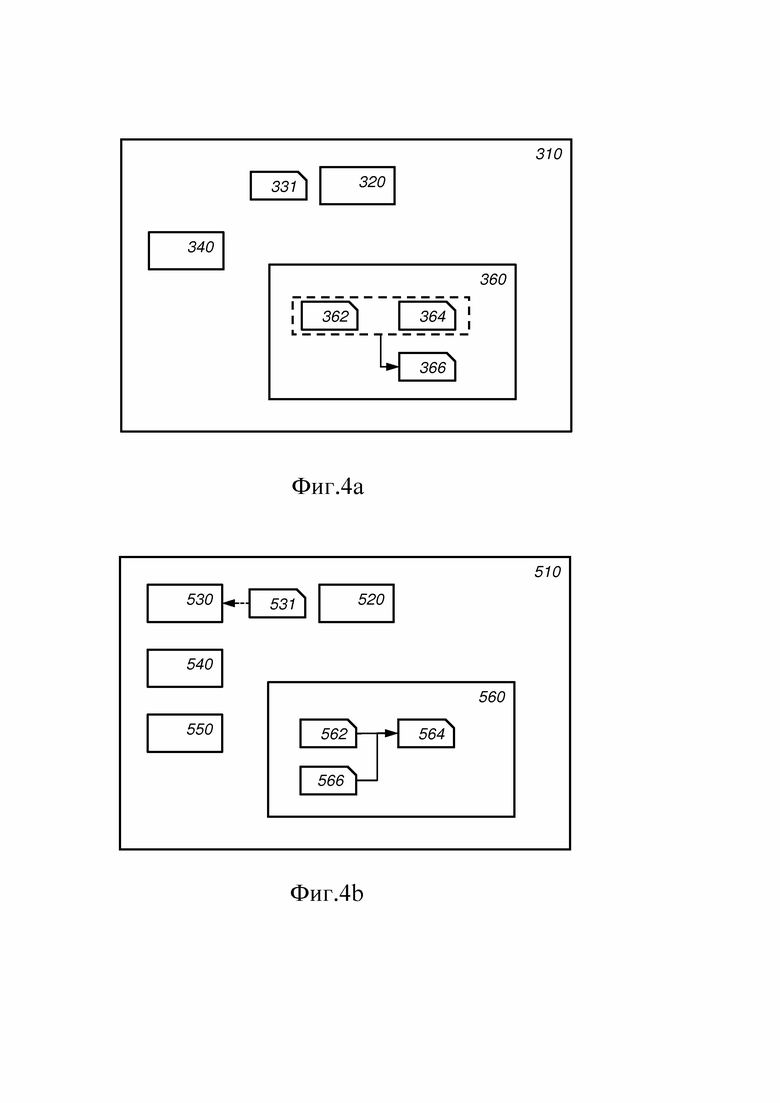
Изобретение относится к сетевому узлу, выполненному для осуществления криптографической операции, способу осуществления криптографической операции и компьютерочитаемому носителю информации. Технический результат заключается в обеспечении безопасной криптографической схемы обмена ключами и достигается за счет того, что первый сетевой узел выполнен с возможностью приема в качестве входа параметра (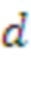 ) сложности и параметра (
) сложности и параметра (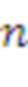 ) структуры и получения общей матрицы (
) структуры и получения общей матрицы ( ), причем общую матрицу совместно используют со вторым сетевым узлом посредством интерфейса связи, элементы в общей матрице
), причем общую матрицу совместно используют со вторым сетевым узлом посредством интерфейса связи, элементы в общей матрице  выбирают по модулю первого модуля (
выбирают по модулю первого модуля (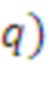 , общая матрица (
, общая матрица ( ) представляет собой квадратную матрицу (
) представляет собой квадратную матрицу (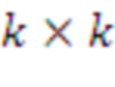 ) размера (
) размера (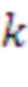 ), равного параметру (
), равного параметру (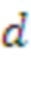 ) сложности, деленному на параметр (
) сложности, деленному на параметр (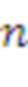 ) структуры, элементы в общей матрице (
) структуры, элементы в общей матрице ( ) являются многочленами по модулю многочлена (
) являются многочленами по модулю многочлена (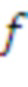 ) приведения степени, равной параметру (
) приведения степени, равной параметру (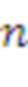 ) структуры, причем указанная криптографическая операция использует общую матрицу. 4 н. и 11 з.п ф-лы, 6 ил., 3 табл.
) структуры, причем указанная криптографическая операция использует общую матрицу. 4 н. и 11 з.п ф-лы, 6 ил., 3 табл.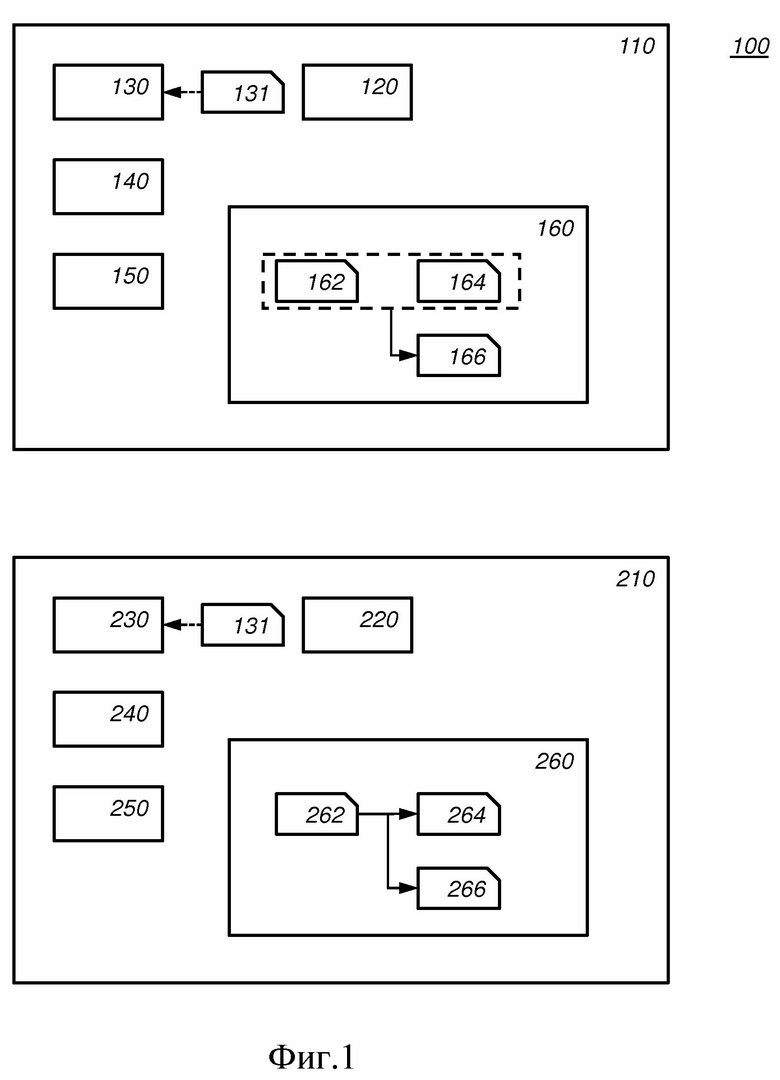
1. Первый узел (110) электронной сети, выполненный с возможностью осуществления криптографической операции с использованием матрицы открытого ключа первого узла электронной сети и содержащий:
- интерфейс (120) связи, выполненный с возможностью осуществления цифровой связи со вторым сетевым узлом,
- схему процессора, выполненную с возможностью:
- приема в качестве входа параметра (d) сложности и параметра (n) структуры,
- получения общей матрицы (А), причем общая матрица совместно используется со вторым сетевым узлом посредством интерфейса связи, общая матрица (А) представляет собой квадратную матрицу (k×k) размера (k), равного параметру (d) сложности, деленному на параметр (n) структуры, элементы в общей матрице (А) представляют собой целочисленные многочлены степени меньше параметра (n) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирования матрицы (S1) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирования матрицы (P1) открытого ключа первого сетевого узла путем:
- вычисления матричного произведения между общей матрицей (А) и матрицей (S1) закрытого ключа по модулю первого модуля (q) и по модулю многочлена (ƒ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, и
- отправки матрицы открытого ключа первого сетевого узла второму сетевому узлу.
2. Первый узел (110) электронной сети по п. 1, в котором схема процессора выполнена с возможностью:
- приема матрицы (PR) открытого ключа второго сетевого узла,
- вычисления необработанного ключа как матричного произведения между принятой матрицей открытого ключа второго узла и матрицей закрытого ключа первого сетевого узла,
при этом первый сетевой узел также выполнен с возможностью:
- приема данных (h) согласования второго сетевого узла,
- вычисления общего ключа или сообщения путем применения функции (rec) согласования к принятым данным согласования и необработанному ключу, или
при этом первый сетевой узел также выполнен с возможностью:
- получения общего ключа или сообщения и получения данных согласования из необработанного ключа,
- отправки данных согласования второму сетевому узлу.
3. Первый сетевой узел по любому из предыдущих пунктов, в котором криптографическая операция является одной из следующих: протокол обмена ключами (KEX), механизм инкапсуляции ключа (KEM), шифрование открытого ключа (PKE), цифровая подпись.
4. Первый сетевой узел по любому из предыдущих пунктов, в котором многочлен приведения представляет собой xn+1 или 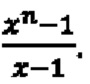
5. Первый сетевой узел по любому из предыдущих пунктов, выполненный с возможностью приема разных параметров (d) сложности и/или разных параметров (n) структуры, причем первый сетевой узел выполнен с возможностью вызова общей части, относящейся к умножению матриц, для разных значений параметра (n) структуры и/или параметра (d) сложности.
6. Первый сетевой узел по любому из предыдущих пунктов, в котором:
- параметр структуры является целым числом, которое не меньше 1 и не больше параметра сложности, и/или
- параметр структуры равен 1 или параметру сложности, и/или
- параметр (n) структуры ограничен тем, что он является простым числом, и/или
- параметр (n) структуры ограничен тем, что он является простым числом, а первый модуль является степенью двойки, и/или
- параметр (n) структуры ограничен тем, что он является простым числом, а первый модуль является степенью двойки и многочлен приведения неприводим по модулю 2.
7. Первый сетевой узел по любому из предыдущих пунктов, в котором схема процессора выполнена с возможностью вычисления расширенной общей матрицы для общей матрицы (А) путем замены элементов многочленов степени больше 0 циркулянтной матрицей, причем указанная расширенная матрица имеет количество столбцов и строк, равное параметру сложности.
8. Первый сетевой узел по любому из предыдущих пунктов, в котором
- криптографическая операция представляет собой формирование открытого ключа, и открытый ключ содержит матрицу открытого ключа первого сетевого узла и общую матрицу или начальное число, из которого ее получают, а закрытый ключ содержит матрицу закрытого ключа, или в котором
- криптографическая операция представляет собой шифрование открытого ключа, и открытый ключ содержит матрицу открытого ключа второго сетевого узла и общую матрицу или начальное число, из которого ее получают.
9. Первый сетевой узел по любому из предыдущих пунктов, в котором добавление шума к элементам в произведении матриц включает умножение несмасштабированного элемента на второй модуль, деление на первый модуль, округление до целого числа и взятие округленного элемента по модулю второго модуля, вычисление необработанного ключа как матричного произведения между принятым открытым ключом второго узла и матрицей закрытого ключа первого сетевого узла, выполняемого по модулю второго модуля (р).
10. Первый сетевой узел по любому из предыдущих пунктов, выполненный с возможностью получения общей матрицы (А) путем формирования матрицы (А) из выхода детерминированного генератора псевдослучайных чисел, затравленного случайным начальным числом, причем общую матрицу совместно используют со вторым сетевым узлом путем отправки или приема случайного начального числа через интерфейс связи.
11. Первый узел (510) электронной сети по любому из предыдущих пунктов, в котором криптографическая операция представляет собой операцию шифрования открытого ключа, причем матрица открытого ключа первого сетевого узла представляет собой первую часть шифртекста, а первый узел электронной сети выполнен с возможностью:
- приема матрицы (P_R) открытого ключа второго сетевого узла,
- вычисления необработанного ключа как матричного произведения между принятой матрицей открытого ключа второго узла и закрытой матрицей первого сетевого узла,
- вычисления второй части шифртекста из необработанного ключа и из сообщения, и
- отправки первой части шифртекста и второй части шифртекста второму сетевому узлу.
12. Первый узел (310) электронной сети, выполненный с возможностью осуществления операции расшифрования открытого ключа, содержащий:
- интерфейс связи, выполненный с возможностью осуществления цифровой связи со вторым сетевым узлом,
- схему процессора, выполненную с возможностью:
- приема в качестве входа параметра (d) сложности и параметра (n) структуры,
- получения матрицы (S1) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- приема первой части (PR) шифртекста и второй части шифртекста от второго сетевого узла, причем первую часть шифртекста и вторую часть шифртекста вычисляют на основе общей матрицы и матрицы открытого ключа первого сетевого узла, а матрицу открытого ключа первого сетевого узла вычисляют из общей матрицы и матрицы закрытого ключа, причем первую часть шифртекста формируют путем вычисления матричного произведения между общей матрицей (А) и закрытой матрицей (S1) по модулю первого модуля (q) и по модулю многочлена (ƒ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления шума к элементам в произведении матриц, причем общая матрица (А) представляет собой квадратную матрицу (k×k) размера (k), равного параметру (d) сложности, деленному на параметр (n) структуры, элементы в общей матрице (А) являются целочисленными многочленами степени меньше параметра (n) структуры, коэффициенты многочленов предпочтительно выбирают по модулю первого модуля (q), элементы в матрице закрытого ключа являются целочисленными многочленами степени меньше параметра (n) структуры,
- вычисления необработанного ключа как матричного произведения между первой частью шифртекста и матрицей закрытого ключа,
- вычисления сообщения из необработанного ключа и второй части шифртекста.
13. Способ (400) электронной криптографической операции для первого узла (110) электронной сети путем выполнения криптографической операции с использованием матрицы открытого ключа первого узла электронной сети, включающий:
- осуществление (410) цифровой связи между первым сетевым узлом и вторым сетевым узлом,
- прием (415) в качестве входа параметра (d) сложности и параметра (n) структуры,
- получение (420) общей матрицы (А), причем общую матрицу совместно используют со вторым сетевым узлом посредством интерфейса связи, общая матрица (А) представляет собой квадратную матрицу (k×k) размера (k), равного параметру (d) сложности, деленному на параметр (n) структуры, элементы в общей матрице (А) представляют собой целочисленные многочлены степени меньше параметра (n) структуры, коэффициенты многочленов предпочтительно выбраны по модулю первого модуля (q),
- формирование (430) матрицы (S1) закрытого ключа, причем элементы в матрице закрытого ключа представляют собой целочисленные многочлены степени меньше параметра (n) структуры,
- формирования (440) матрицы (P1) открытого ключа первого сетевого узла путем:
- вычисления (442) матричного произведения между общей матрицей (А) и матрицей (S1) закрытого ключа по модулю первого модуля (q) и по модулю многочлена (ƒ) приведения со степенью, равной параметру (n) структуры, получения произведения матриц и добавления (444) шума к элементам в произведении матриц,
- отправку (452) матрицы открытого ключа первого сетевого узла второму сетевому узлу.
14. Первый узел электронной сети по любому из пп. 1-11, в котором добавление шума к элементам в произведении матриц включает уменьшение масштаба элементов в произведении матриц.
15. Компьютерочитаемый носитель (1000) информации, содержащий кратковременные и некратковременные данные (1020), представляющие инструкции, выполнение которых процессорной системой приводит к осуществлению ею способа по п. 13.
| US 9673977 B1, 06.06.2017 | |||
| WO 2016162941 A1, 13.10.2016 | |||
| JP 2007151073 A, 14.06.2007 | |||
| US 20120155635 A1, 21.06.2012 | |||
| US 8938623 B2, 20.01.2015 | |||
| СПОСОБ ЗАЩИЩЕННОЙ СВЯЗИ В СЕТИ, УСТРОЙСТВО СВЯЗИ, СЕТЬ И КОМПЬЮТЕРНАЯ ПРОГРАММА ДЛЯ ЭТОГО | 2009 |
|
RU2528078C2 |
| СПОСОБ ПОРОГОВОЙ ГЕНЕРАЦИИ КЛЮЧЕЙ ДЛЯ СИСТЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ НА ОСНОВЕ ИДЕНТИФИКАЦИОННЫХ ДАННЫХ | 2010 |
|
RU2452111C1 |
Авторы
Даты
2021-07-30—Публикация
2018-10-10—Подача