Изобретение относится к области медицины, в частности - к ультразвуковой диагностике, и может использоваться в системах ультразвуковой визуализации.
В последние годы методы статистической обработки сигналов широко используются в различных областях науки как эффективный инструмент анализа стохастических данных различной природы. Стохастические данные, получаемые при построении ультразвуковых изображений в В-режиме при исследовании биологических структур, характеризуемых наличием большого числа однородных отражателей, адекватно описываются статистической моделью Райса [1, 2].
Из уровня техники известны работы, в которых статистические методы обработки данных используются для характеризации исследуемой среды. Так, в работах [3, 4]. методами статистического анализа эхо-сигнала оценивалась концентрация рассеивателей в среде. В этих работах эхо-сигнал анализируется путем расчета параметра распределения Накагами как адекватно описывающего некоторые задачи, связанные с рассеянием ультразвука. Параметры распределения Накагами исследовались прежде всего, как показатели, характеризующие концентрацию рассеивателей. Однако недостатки методов, предлагаемых в данных работах, обусловлены как ограниченной применимостью распределения Накагами для описания процессов ультразвуковой визуализации, так и невозможностью в рамках применяемых в этих работах методов решения задачи получения количественных оценок размеров диагностируемых неоднородностей.
Заявляемое изобретение направлено на решение задачи определения размера структурных образований исследуемой среды при ультразвуковой визуализации.
Сопоставляя заявляемый способ решения данной задачи и аналоги [3, 4], целесообразно отметить, что, хотя в обоих случаях основным инструментом решения поставленной задачи является изучение статистических характеристик эхо-сигнала, тем не менее, заявляемый способ существенно отличается от аналогов следующими особенностями:
- в заявляемом изобретении решается задача количественного оценивания размеров рассеивающих неоднородностей, в то время как в работах [3, 4] определяется концентрация рассеивателей в рамках применимости статистического распределения Накагами; - для решения поставленной в заявляемом изобретении используется статистическая модель Райса как адекватно описывающая исследуемые процессы формирования эхо-сигнала, в то время как статистическая модель Накагами, как известно, используется с определенными допущениями, для упрощения решения ряда задач и имеет ограниченную применимость для описания статистики эхо-сигнала. Решение задачи определения размера неоднородностей среды на основании выявления заметной когерентной составляющей в эхо-сигнале при переходе рэлеевского распределения в райсовское является принципиально новым.
Распределение Райса и его частный случай - распределение Рэлея - в ультразвуковой визуализации соответствуют распределению амплитуды изображения в В-режиме при достаточно однородном составе отражателей и их высокой плотности, причем изображение формируется огибающей радиочастотного сигнала. При этом в отсутствии когерентной компоненты сигнала мы имеем дело с распределением Рэлея, в то время как распределение Райса соответствует случаю высокой плотности случайных отражателей, но при этом в составе сигнала присутствует и заметная когерентная составляющая
В основе предлагаемого способа лежит зависимость степени когерентности рассеянного ультразвукового сигнала от соотношения геометрических параметров ультразвукового луча и рассеивающих неоднородностей. А именно: по мере приближения к фокальной плоскости и сужения луча количество некоррелированных между собой рассеивателей, попадающих в область луча, уменьшается, и при этом рэлеевское распределение, характеризующее рассеяние звука многими некоррелированными неоднородностями, переходит в распределение Райса, характеризующее эхо-сигнал со значительной когерентной составляющей, когда в области луча оказывается практически всего один рассеиватель. Такой переход от рэлеевского распределения эхо-сигнала к райсовскому имеет место на той глубине, где ширина луча соответствует размеру рассеивающей неоднородности, и соответствует переходу от полностью некогерентного рассеяния к появлению значительной когерентной составляющей в эхо-сигнале. Таким образом, выявление факта такой трансформации одного распределения в другое используется в заявляемом техническом решении как инструмент определения размера структурных неоднородностей исследуемой среды как величины, соотносимой с размером области когерентности при рассеянии ультразвуковой волны.
Распространение ультразвуковой волны в среде описывается основным уравнением акустики, конкретное решение которого однозначно определяется свойствами рассеивающей неоднородной среды, в первую очередь - флуктуациями плотности и сжимаемости. Записанное относительно Фурье-преобразования 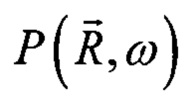 пространственно-временной функции давления
пространственно-временной функции давления 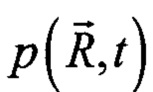 , данное уравнение имеет следующий вид [2]:
, данное уравнение имеет следующий вид [2]:
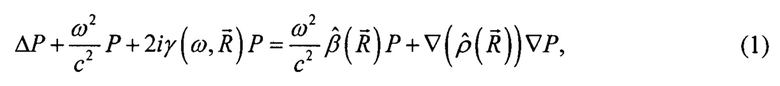
где ω - частота, t - время, с=(ρ0β0)-1/2 - скорость звука в среде с плотностью ρ0 и сжимаемостью 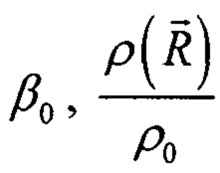 - относительное изменение плотности,
- относительное изменение плотности, 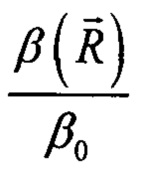 - относительное изменение сжимаемости среды,
- относительное изменение сжимаемости среды, 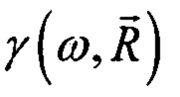 - преобразование Фурье функции поглощения звука в среде,
- преобразование Фурье функции поглощения звука в среде, 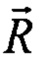 - пространственная координата рассматриваемой точки среды. Как правило, выше приведенное уравнение для спектральной плотности функции давления
- пространственная координата рассматриваемой точки среды. Как правило, выше приведенное уравнение для спектральной плотности функции давления 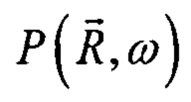 решается в борновском приближении.
решается в борновском приближении.
Функция давления как основная характеристика процесса распространения звука в среде представляет собой комплексную величину и характеризуется амплитудой и фазой. В процессе распространения по неоднородной среде величина рассеянного сигнала неизбежно искажается спекл-шумом, образованным суммированием многих независимых компонент от рассеяния звуковой волны точечными отражателями и поэтому обладающим гауссовской статистикой. Результирующая функция давления и, соответственно, значение эхо-сигнала может быть представлена как сумма некоторой детерминированной величины и искажающей его шумовой компоненты с гауссовской статистикой.
Рассмотрим искомую комплексную величину пространственно-временной функции давления 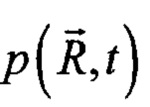 в конкретной точке пространства
в конкретной точке пространства 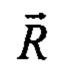 и в момент времени t:
и в момент времени t:
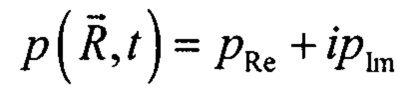 как случайную величину, формируемую некой изначально детерминированной составляющей и гауссовским шумом с дисперсией σ2. Обозначим амплитуду детерминированной компоненты функции давления в конкретной точке
как случайную величину, формируемую некой изначально детерминированной составляющей и гауссовским шумом с дисперсией σ2. Обозначим амплитуду детерминированной компоненты функции давления в конкретной точке 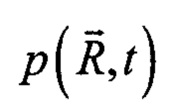 как А. При этом действительная pRe и мнимая pIm части измеряемого и анализируемого комплексного сигнала искажаются гауссовским шумом независимо. Тогда действительная pRe и мнимая pIm компоненты анализируемой комплексной величины представляют собой независимые гауссовские величины с одинаковыми дисперсиями σ2 и ненулевыми математическими ожиданиями, в то время как амплитуда
как А. При этом действительная pRe и мнимая pIm части измеряемого и анализируемого комплексного сигнала искажаются гауссовским шумом независимо. Тогда действительная pRe и мнимая pIm компоненты анализируемой комплексной величины представляют собой независимые гауссовские величины с одинаковыми дисперсиями σ2 и ненулевыми математическими ожиданиями, в то время как амплитуда 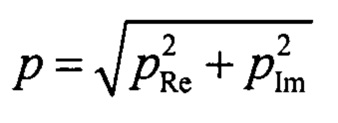 результирующего сигнала, как известно, подчиняется распределению Райса с параметрами А и σ2. Функция плотности вероятности распределения Райса определяется выражением [1]:
результирующего сигнала, как известно, подчиняется распределению Райса с параметрами А и σ2. Функция плотности вероятности распределения Райса определяется выражением [1]:
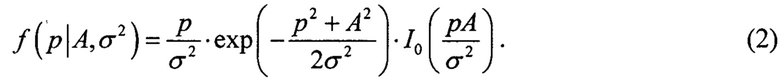
Оба параметра статистического распределения Райса в выражении (2) имеют конкретный физический смысл: σ2 - это дисперсия искажающего сигнал гауссовского шума, а параметр А совпадает с величиной амплитуды исходного детерминированного сигнала, с чем связана значимость задачи как можно более точного оценивания этого параметра при анализе данных. Задача совместного определения обоих параметров сигнала А и шума σ на основе выборочных измерений pi(i=1, 2, …, n) суммарного сигнала р может быть эффективно решена методами двухпараметрического анализа данных [5-7]. Именно эти методы используются в качестве математического инструмента при проведении статистического анализа эхо-сигнала при решении задачи определения размера неоднородности среды.
В качестве примера приведем формулы для вычисления искомых райсовских параметров двухпараметрическим методом моментов, основанным на анализе данных выборочных измерений 2-го и 4-го моментов и в силу этого обозначаемого как ММ24. Известно, что для 2-го и 4-го начальных моментов случайной величины р, подчиняющейся распределению Райса с параметрами (A, σ2), справедливы следующие формулы:

Эти формулы представляют собой простую систему двух уравнений для двух неизвестных А и σ2. В решении данной системы и состоит метод ММ24, [7]. Для определения искомых параметров А и σ2 данным методом нетрудно получить следующие выражения:

Где 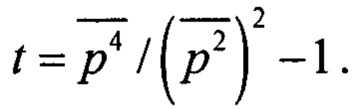 Нетрудно видеть, что для любой случайной величины р в силу стохастичности величины р2 выполняется условие
Нетрудно видеть, что для любой случайной величины р в силу стохастичности величины р2 выполняется условие 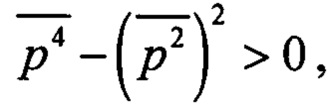 так как разность
так как разность 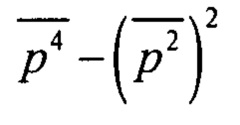 определяет дисперсию случайной величины р2. Поэтому введенный параметр t растет с ростом стохастичности процесса и удовлетворяет соотношению: 0<t≤1. Предельный случай t=1 соответствует частному случаю распределения Райса - распределению Рэлея, когда присутствует гауссовский шум, а детерминированная составляющая сигнала отсутствует (А=0).
определяет дисперсию случайной величины р2. Поэтому введенный параметр t растет с ростом стохастичности процесса и удовлетворяет соотношению: 0<t≤1. Предельный случай t=1 соответствует частному случаю распределения Райса - распределению Рэлея, когда присутствует гауссовский шум, а детерминированная составляющая сигнала отсутствует (А=0).
Таким образом, рассчитывая по формуле (4) параметры статистического распределения эхо-сигнала на основе его выборочных измерений, и, прежде всего -величину амплитуды А, мы можем определить, какое именно распределение - Райса или Рэлея - характеризует эхо-сигнал, формирующий ультразвуковое изображение, и таким образом выявить момент перехода от одного распределения к другому. Соответствующий данному моменту размер фокальной перетяжки будет характеризовать искомый размер структурных неоднородностей исследуемой среды.
Физическая сущность заявляемого способа состоит в следующем. Большинство схем построения изображения в приборах ультразвуковой визуализации основаны на регистрации импульса, рассеянного в обратном направлении, причем в диагностических приборах как правило имеется возможность перемещения фокальной плоскости вглубь среды.
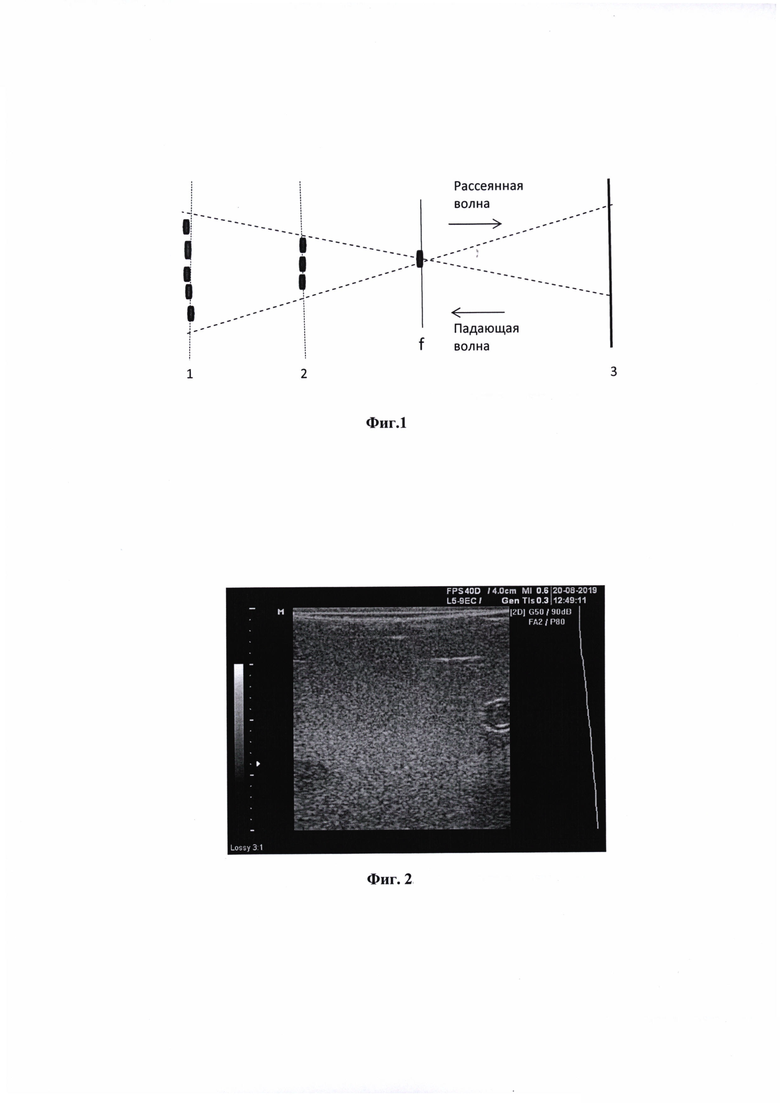
На Фиг. 1 схематически иллюстрируется процесс рассеяния на неоднородностях среды. Плоскость, на которой в данный момент сфокусировано излучение, обозначена буквой f. Для примера показаны две другие плоскости в рассеивающей среде, обозначенные цифрами 1 и 2. Они находятся вне фокуса, и в этих плоскостях расфокусированный падающий луч имеет достаточно большую ширину, так что в пределах луча помещаются несколько рассеивающих неоднородностей. Плоскость излучения и приема ультразвуковых сигналов условно показана в правой части рисунка и обозначена цифрой 3 (конструктивные детали, такие как линзы, отдельные датчики излучающей и принимающей сигналы фазовой решетки в данной схематичной иллюстрации не детализированы, а условно объединены в плоскости 3).
Очевидно, что статистические особенности регистрируемого приемником рассеянного сигнала определяются взаимодействием сигналов, рассеянных отдельными неоднородностями среды, и их взаимной когерентностью: сигнал, регистрируемый с плоскости 1, находящейся на значительном расстоянии от фокальной плоскости f, будет формироваться рассеянием от большого количества неоднородностей, которые как правило являются независимыми, раскоррелированы по фазам, и поэтому результаты рассеяния различными неоднородностями, находящимися в плоскости 1, будут «гасить» друг друга и результирующий рассеянный ими сигнал будет подчиняться распределению Рэлея. По мере уменьшения в зоне луча количества рассеивающих неоднородностей рассеяние от каждой из них все в меньшей степени будет «гаситься» рассеянием от соседних неоднородностей. При этом результирующий сигнал из рэлеевского будет трансформироваться в райсовский, имеющим ненулевую детерминированную составляющую амплитуды. И, наконец, если в зоне луча будет находиться только одна рассеивающая неоднородность (что возможно достичь в фокальной плоскости или на некотором расстоянии от нее, когда размер луча сужается до размера рассеивателя), то рассеяние от этой неоднородности вообще не будет «гаситься» соседними рассеивателями, и яркость соответствующих точек на изображении, формируемом рассеянным излучением, будет заметно выше. В этом случае рассеянный сигнал подчиняется статистическому распределению Райса как сигнал, имеющий отличную от нуля детерминированную составляющую амплитуды, превышающую уровень фонового шума,
Таким образом, усиление яркости изображения в фокальной плоскости, связанное с наличием в отраженной волне сильной когерентной составляющей, свидетельствует о переходе рэлеевского статистического распределения амплитуды эхо-сигнала в райсовское, и размер структурных неоднородностей исследуемой среды при этом можно оценить как величину фокальной перетяжки луча, соответствующую такому переходу.
На Фиг. 2 представлены результаты физического эксперимента, реализующего заявляемое изобретение. В ходе эксперимента с помощью ультразвукового прибора Medison Sonoace 8000 EX Prime с линейным датчиком L5-9EC было проведено исследование отражения ультразвука в фантоме с однородной структурой рассеивателей размером примерно 0,3 мм. Как видно из представленного ниже изображения (Фиг. 2), в зоне ультразвукового изображения, соответствующей рассеянию сигнала от области, расположенной вблизи фокальной плоскости, действительно наблюдается повышение яркости. Такое повышение яркости, несмотря на уменьшение рассеивателей при сужении пучка по мере приближения к фокальной зоне, наблюдалось для определенного размера рассеивающих неоднородностей, который соответствовал размеру луча в фокальной перетяжке, что подтверждает реализуемость заявляемого способа определения размеров неоднородностей посредством статистического анализа эхо-сигнала.
Оценивая ширину фокальной перетяжки, соответствующую увеличению яркости в вышеприведенном эксперименте, по известной формуле:

где F - расстояние от апертуры до фокальной позиции, λ - длина волны, D - ширина апертуры, получаем для размера структурных образований, формирующих ультразвуковое изображение в данном эксперименте, величину порядка 0,2 мм.
Таким образом, осуществление заявляемого изобретения состоит в следующей последовательности действий и измерений:
- на основе выборочных измерений амплитуды эхо-сигнала методами двухпараметрического анализа райсовских данных рассчитывают значения райсовских параметров сигнала и шума;
- определяют глубину, которой соответствует эхо-сигнал с наибольшей яркостью;
- определяют поперечные размеры луча, соответствующие данной глубине;
- размер неоднородности, рассеяние на которой формирует эхо-сигнал максимальной яркости, принимают соответствующим поперечному размеру луча на глубине, с которой приходит эхо-сигнал максимальной яркости.
СПИСОК ЛИТЕРАТУРЫ
1. Rice S. О. Mathematical Analysis of Random Noise // Bell Syst. Tech. Journal. 1944. Vol. 23. P. 282-322.
2. Physical Principles of Medical Ultrasonics, 2nd Edition, C.R. Hill (Editor), J.C. Bamber (Editor), G.R. ter Haar (Editor), ISBN: 978-0-471-97002-6, March 2004, 528 P.
3. Tsui, PH, Wan, YL, Tai, DI, Shu, YC. Effects of estimators on ultrasound Nakagami imaging in visualizing the change in the backscattered statistics from a Rayleigh distribution to a pre-Rayleigh distribution. Ultrasound Med Biol. 2015;41:2240-51, DOI: 10.1016/j.ultrasmedbio.2015.04.003.
4. Lin JJ, Cheng JY, Huang LF, Lin YH, Wan YL, Tsui PH. Detecting changes in ultrasound backscattered statistics by using Nakagami parameters: Comparisons of moment-based and maximum likelihood estimators. Ultrasonics, 2017; 77:133-43, doi: 10.1016/j.ultras.2017.02.006. Epub 2017 Feb 9.
5. Т.В. Яковлева, H.C. Кульберг Способ двухпараметрического анализа случайных сигналов / Патент на изобретении №2555501, 2015 (правообладатель - ФИЦ ИУ РАН).
6. Т.В. Яковлева, Н.С. Кульберг Способ двухпараметрического анализа случайных сигналов на основе измеренных данных для 1-го и 2-го моментов / Патент на изобретении №2556319, 2015 (правообладатель - ФИЦ ИУ РАН).
7. Т.В. Яковлева, Н.С. Кульберг Способ двухпараметрического анализа случайных сигналов на основе измеренных данных для 2-го и 4-го моментов / Патент на изобретении №2556318, 2015 (правообладатель - ФИЦ ИУ РАН).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ НА ОСНОВЕ ИЗМЕРЕННЫХ ДАННЫХ ДЛЯ 2-ГО И 4-ГО МОМЕНТОВ | 2014 |
|
RU2556318C1 |
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ НА ОСНОВЕ ИЗМЕРЕННЫХ ДАННЫХ ДЛЯ 1-ГО И 2-ГО МОМЕНТОВ | 2014 |
|
RU2556319C1 |
| СПОСОБ ОЦЕНКИ СВЕТОРАССЕЯНИЯ В ОПТИЧЕСКИХ СРЕДАХ ГЛАЗА | 2000 |
|
RU2172134C1 |
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ | 2014 |
|
RU2555501C1 |
| Способ определения акустической плотности | 2017 |
|
RU2657314C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАЗМЕРОВ ЧАСТИЦ | 1992 |
|
RU2035036C1 |
| УСТРОЙСТВО И СПОСОБ ИЗМЕРЕНИЯ КРОВЯНОГО ДАВЛЕНИЯ | 2016 |
|
RU2648029C2 |
| Акустический корреляционныйСпОСОб изМЕРЕНия СКОРОСТи пОТОКАжидКОСТи | 1979 |
|
SU808937A1 |
| УСТРОЙСТВО ДЛЯ ДИАГНОСТИКИ | 2005 |
|
RU2408280C2 |
| Устройство для демонстрации явлений интерференции и дифракции света | 1989 |
|
SU1622897A1 |
Изобретение относится к медицинской технике, в частности к ультразвуковой диагностике, и может использоваться в системах ультразвуковой визуализации. Изобретение направлено на решение задачи определения размера структурных образований исследуемой среды при ультразвуковой визуализации. Для этого используется статистическая модель Райса как адекватно описывающая исследуемые процессы формирования эхо-сигнала при достаточно однородном составе отражателей и их высокой плотности, причем изображение формируется огибающей радиочастотного сигнала. В основе предлагаемого способа лежит зависимость степени когерентности рассеянного ультразвукового сигнала от соотношения геометрических параметров ультразвукового луча и рассеивающих неоднородностей. Существенным является выявление заметной когерентной составляющей в эхо-сигнале при переходе рэлеевского распределения в райсовское, что сопровождается заметным усилением яркости изображения в фокальной плоскости. Размер неоднородности, рассеяние на которой формирует эхо-сигнал максимальной яркости, оценивают как соответствующий поперечному размеру луча на глубине, с которой приходит эхо-сигнал максимальной яркости. 2 ил.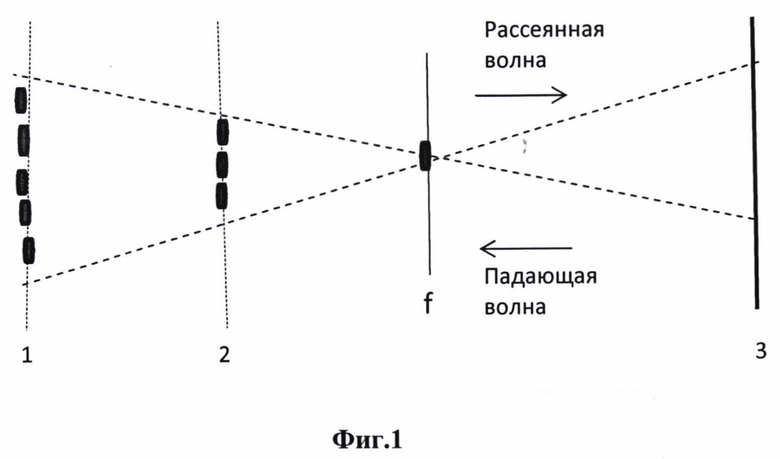
Способ определения размера структурных образований при ультразвуковой визуализации, характеризующийся тем, что в системе ультразвуковой визуализации формируют ультразвуковое изображение,
отличающийся тем, что
- на основе выборочных измерений амплитуды эхо-сигнала методами двухпараметрического анализа райсовских данных рассчитывают значения райсовских параметров сигнала и шума;
- определяют глубину, которой соответствует эхо-сигнал с наибольшей яркостью;
- определяют поперечные размеры луча, соответствующие данной глубине;
- размер неоднородности, рассеяние на которой формирует эхо-сигнал максимальной яркости, принимают соответствующим поперечному размеру луча на глубине, с которой приходит эхо-сигнал максимальной яркости.
| СПОСОБ ОПРЕДЕЛЕНИЯ СРЕДНЕГО ДИАМЕТРА ЗЕРНА МЕТАЛЛИЧЕСКИХ ИЗДЕЛИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2589751C2 |
| WO 9937364 A1, 29.07.1999 | |||
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ | 2014 |
|
RU2555501C1 |
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ НА ОСНОВЕ ИЗМЕРЕННЫХ ДАННЫХ ДЛЯ 1-ГО И 2-ГО МОМЕНТОВ | 2014 |
|
RU2556319C1 |
| СПОСОБ ДВУХПАРАМЕТРИЧЕСКОГО АНАЛИЗА СЛУЧАЙНЫХ СИГНАЛОВ НА ОСНОВЕ ИЗМЕРЕННЫХ ДАННЫХ ДЛЯ 2-ГО И 4-ГО МОМЕНТОВ | 2014 |
|
RU2556318C1 |
Авторы
Даты
2022-10-17—Публикация
2021-12-24—Подача