Изобретение относится к области электротехники, и может быть использовано при производстве и эксплуатации электрических трансформаторов, в том числе, силовых.
Согласно ГОСТ Р 57700.37-2021 [ГОСТ Р 57700.37 – 2021 Компьютерные модели и моделирование. Цифровые двойники изделий. Общие положения: национальный стандарт РФ. – М.: Федеральное агентство по техническому регулированию и метрологии, 2021 – Дата утверждения 16.09.2021.] под цифровым двойником изделия (ЦД) понимается «система, состоящая из цифровой модели изделия и двусторонних информационных связей с изделием (при наличии изделия) и (или) его составными частями». При этом цифровая модель изделия – это «система математических и компьютерных моделей, а также электронных документов изделия, описывающая структуру, функциональность и поведение вновь разрабатываемого или эксплуатируемого изделия на различных стадиях жизненного цикла, для которой на основании результатов цифровых и (или) иных испытаний по ГОСТ 16504 выполнена оценка соответствия предъявляемым к изделию требованиям». Там же: «Цифровая модель должна описывать структуру, функциональность и поведение разрабатываемого или эксплуатируемого изделия на тех стадиях жизненного цикла, которые установлены в соответствующих технических заданиях».
Классификация и основные требования, предъявляемые к ЦД электротехнического оборудования, в частности, к ЦД электрических трансформаторов (ЭТ), приведены в [Дарьян Л.А., Конторович Л.Н. Цифровые двойники электроэнергетического оборудования – основные принципы и технические требования. – Электроэнергия. Передача и распределение, № 5 (62) 2020. – с. 45 – 57.]. Как следует из [Дарьян Л.А., Конторович Л.Н. Цифровые двойники электроэнергетического оборудования – основные принципы и технические требования. – Электроэнергия. Передача и распределение, № 5 (62) 2020. – с. 45 – 57.], ЦД ЭТ могут быть использованы на разных стадиях жизненного цикла изделия для имитационного и прогнозного моделирования.
Известен способ пост Rmu – активное сопротивление ветви намагничивания в Т-образной схеме замещения с параллельным включением элементов ветви намагничивания; k1 = k2 = k роения ЦД ЭТ на основе данных о работе реального оборудования, предложенный в [State Evaluation of Power Transformer Based on Digital Twin // [Электронный ресурс]. – Режим доступа: https://ieeexplore.ieee.org/document/8955043 (18.11.2022)]. В качестве основы для создания ЦД здесь выступает имитационная модель, позволяющая имитировать работу реального устройства в различных режимах в целях оценки выхода за допустимые пределы значений величин, характеризующих работу устройства в данных режимах. После построения модель корректируется (калибруется) по результатам измерений с использованием системы датчиков, собирающих данные с реального трансформатора. Такой ЦД, калиброванный на реальном устройстве, может точно отражать особенности и состояния моделируемого оборудования. К недостаткам данного ЦД можно отнести тот факт, что имитационная модель, приведенная здесь, не позволяет отображать тонкие особенности изменения мгновенных значений величин в произвольных режимах работы ЭТ, от чего зачастую зависит протекание специфических процессов, приводящих к авариям.
Известен также способ построения ЦД технических устройств, основанный на построении имитационных моделей с использованием моделей электрических (и других физических) цепей, а также 2D- и 3D-моделей физических полей. Наиболее ярким представителем данного направления является фирма ANSYS, поставляющая на рынок компьютерных технологий пакет Twin Builder, предназначенный для создания и использования в инженерной практике ЦД технических устройств широкого спектра исполнений [ANSYS Twin Builder // [Электронный ресурс]. – Режим доступа: https://cae-expert.ru/product/ansys-twin-builder (18.11.2022)]. В плане способа создания ЦД ЭТ особенно интересна возможность комбинации в рамках единой имитационной модели двух моделей: модели электрической цепи, в которую включены обмотки трансформатора, и модели магнитного поля трансформатора. В частности, это позволяет рассчитать переходные процессы в трансформаторе с учетом взаимного влияния обмоток не только по магнитному полю в магнитопроводе, но и по магнитному полю за пределами магнитопровода. В результате можно построить модель, способную точно отображать характер изменения во времени мгновенных значений величин, характеризующих работу трансформатора в произвольных режимах работы.
К недостаткам данного способа можно отнести:
1) жесткую привязку к конкретному дорогостоящему пакету численного моделирования, требующего высокой компетенции пользователей;
2) повышенную требовательность к компьютерным ресурсам (например, имитационная модель с использованием полевых моделей может рассчитываться часами, при этом полученная точность расчетов сомнительна, особенно при учете магнитных полей за пределами магнитопровода [Тихонов А.И., Пайков И.А. Анализ моделей для электромагнитного расчета силовых трансформаторов // Вестник ИГЭУ. – 2015. – Вып. 3. – с. 38 – 43.]);
3) невозможность получения точного решения, совпадающего с решением, полученным на реальном трансформаторе ввиду различия заявленных в каталогах магнитных характеристик электротехнических сталей и реальных характеристик, фиксируемых после сборки трансформатора, а также ввиду невозможности точного учета влияния на цифровую модель всех факторов технологического характера.
Наиболее близким к предлагаемому изобретению является имитационная модель однофазного электрического трансформатора (ОЭТ), основанная на использовании модели идеального трансформатора с учетом нелинейности кривой намагничивания и электромагнитного гистерезиса, используемая в библиотеке SimPowerSystems, интегрированной в систему имитационного моделирования MatLab Simulink [MathWorks. Simulink // [Электронный ресурс]. – Режим доступа: https://la.mathworks.com/products/simulink.html?s_tid=hp_products_simulink (18.11.2022)]. Описание модели идеального трансформатора приведено в [Ideal Transformer. Help Center. MathWorks. – Режим доступа: https://www.mathworks.com/help/sps/ref/nonlineartransformer.html (18.11.2022)]. Описание имитационной модели реального нелинейного трансформатора приведено в [Nonlinear Transformer. Help Center. MathWorks. – Режим доступа: https://www.mathworks.com/help/sps/ref/nonlineartransformer.html (18.11.2022)]. Для моделирования гистерезисных явлений сами разработчики имитационной модели ОЭТ использовали математический аппарат, описанный в [Casoria, S., P. Brunelle, and G. Sybille, «Hysteresis Modeling in the MATLAB/Power System Blockset», Electrimacs 2002, École de technologie supérieure, Montreal, 2002.; Frame, J.G., N. Mohan, and Tsu-huei Liu, «Hysteresis modeling in an Electro-Magnetic Transients Program», presented at the IEEE PES winter meeting, New York, January 31 to February 5, 1982.].
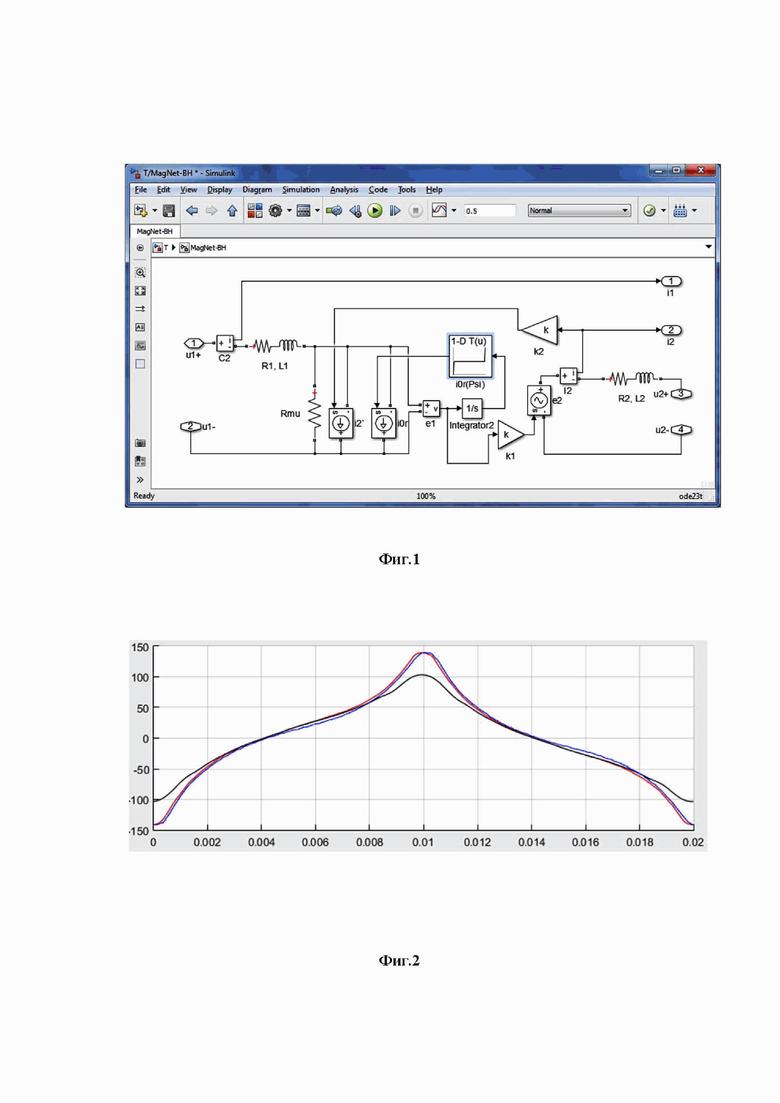
В частности, для моделирования однофазного трансформатора используется цепная модель, приведенная на фиг. 1 - Имитационная модель однофазного трансформатора с использованием кривой намагничивания в форме i0r(Ψ1), реализованная в MatLab Simulink SimPowerSystems. Здесь R1, R2 – активные сопротивления первичной и вторичной обмоток; L1, L2 – индуктивности рассеяния обмоток в опыте трехфазного короткого замыкания (КЗ); Rmu – активное сопротивление ветви намагничивания в Т-образной схеме замещения с параллельным включением элементов ветви намагничивания; k1 = k2 = k – коэффициент трансформации трансформатора; I2’ – управляемый источник тока, на управляющий вход которого подается мгновенное значение приведенного тока вторичной обмотки i2’ = i2.k; i2 – мгновенное значение реального тока вторичной обмотки, фиксируемое измерителем тока во вторичной ветви I2; I0r’ – управляемый источник тока, на управляющий вход которого подается мгновенное значение намагничивающего тока, вычисляемого по кривой намагничивания трансформатора, заданной в форме i0r(Ψ1), звеном табличной зависимости i0r(Ψ1); Ψ1 – потокосцепление первичной обмотки с основным потоком трансформатора, фиксируемое на выходе интегратора 1/s, то есть вычисляемое по формуле
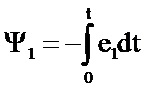 ; (1)
; (1)
e1 – мгновенное значение ЭДС первичной обмотки, фиксируемое измерителем напряжения e1; e2 – управляемый источник ЭДС, на управляющий вход которого подается мгновенное значение ЭДС вторичной обмотки e2 = e1.k; u1-, u1+, u2-, u2+ – электрические контакты на концах соответственно первичной и вторичной обмоток.
Данная модель имеет три недостатка, не позволяющие использовать эту модель без доработок в качестве ЦД ОЭТ, способного при численном исследовании в произвольных режимах работы трансформатора выдавать те же результаты, что и реальное устройство.
Первый недостаток связан с некорректностью задания кривой намагничивания в модели. Так, в частности, в [Nonlinear Transformer Characteristics. Help Center. MathWorks. – Режим доступа: https://la.mathworks.com/help/sps/ug/nonlinear-transformer-characteristics.html (18.11.2022)] разработчики советуют рассчитывать кривую намагничивания, используя «базовый поток, определяемый как пиковое значение синусоидального потока (в веберах), когда обмотка 1 подключена к источнику синусоидального напряжения в 1 о.е.».
Проведенное нами исследование [Подобный А.В. Методика создания цифровых двойников трансформатора на основе корректируемых по результатам эксперимента имитационных моделей: дис. … канд. техн. наук: 05.13.12: защищена 21.09.2022 / Подобный Александр Викторович. – Иваново, 2022. – 141 с.], показывает, что результат моделирования, действительно, существенно зависит от точности задания кривой намагничивания трансформатора. В частности, на фиг. 2 приведены три кривые установившегося тока ХХ однофазного трансформатора, т.е. осциллограмма первичного напряжения и первичного тока в опыте ХХ на одном периоде в установившемся режиме.
Кривая 1 получена из эксперимента на реальном трансформаторе (в качестве объекта исследований выбран однофазный трансформатор малой мощности ОСМ1-0,063ЗУЗ). Кривая 2 получена по результатам моделирования на модели, приведенной на фиг. 1, в которой кривая намагничивания была рассчитана по результатам серии опытов ХХ на реальном трансформаторе при разных действующих значениях питающего напряжения. Из рисунка видно, что отличие в значении амплитуды тока ХХ от экспериментального значения составляет около 40 мА, то есть 29%. Кривая 3 получена на модели, предлагаемой в данном изобретении. При этом результаты моделирования практически совпали с экспериментальной осциллограммой (незначительное смещения кривых 1 и 3 по оси t вызвано действием фильтра, примененного для очистки экспериментальной осциллограммы от высокочастотных шумов).
Таким образом кривая намагничивания должна строиться именно с учетом мгновенных значений тока и напряжения первичной цепи. Любые упрощения, связанные с использованием действующих значений тока и напряжения или сведения реальной формы кривой к синусоиде (как это предлагается в [Nonlinear Transformer Characteristics. Help Center. MathWorks. – Режим доступа: https://la.mathworks.com/help/sps/ug/nonlinear-transformer-characteristics.html (18.11.2022)]), приводят к существенному возрастанию погрешности при расчете мгновенных значений характерных величин на имитационной модели.
При использовании кривых намагничивания трансформатора, полученных из расчета по кривой намагничивания стали, взятой из каталога, отличия результатов моделирования от результатов эксперимента могут быть непредсказуемыми. Так фиг. 3. Показан установившийся ток ХХ, полученный с использованием разных кривых намагничивания, т.е. на фиг. 3 приведены три кривые, полученные на моделях с разными кривыми намагничивания трансформатора: 1 – модель с кривой намагничивания, полученной по методике, приведенной в данном изобретении, дающей результаты, совпадающие с результатами эксперимента, 2 – модель с кривой намагничивания, полученной из опыта ХХ; 3 – модель с кривой намагничивания, полученной расчетным путем по кривой намагничивания электротехнической стали 3408, взятой из каталога [Прокат холоднокатанный тонколистный их электротехнической анизотропной стали / Каталог продукции. – Новолипецкий металлургический комбинат. – 39 с. – Режим доступа: http://facts-plus.com/forum_files/Tech/MAG/NLMK.pdf]. Погрешность в определении амплитудного значения установившегося тока ХХ в последнем случае составила 114%.
Второй недостаток связан с некорректностью учета явления электромагнитного гистерезиса в модели, претендующей на право считаться цифровым двойником реального трансформатора. Как отмечалось, для учета гистерезиса в модели трансформатора в MatLab Simulink SimPowerSystems использованы работы [Casoria, S., P. Brunelle, and G. Sybille, «Hysteresis Modeling in the MATLAB/Power System Blockset», Electrimacs 2002, École de technologie supérieure, Montreal, 2002.; Frame, J.G., N. Mohan, and Tsu-huei Liu, «Hysteresis modeling in an Electro-Magnetic Transients Program», presented at the IEEE PES winter meeting, New York, January 31 to February 5, 1982.]. В то же время, например, в [Casoria, S., P. Brunelle, and G. Sybille, «Hysteresis Modeling in the MATLAB/Power System Blockset», Electrimacs 2002, École de technologie supérieure, Montreal, 2002.], подчеркивается, что речь здесь идет о модели статического гистерезиса без учета влияния на него вихревых токов в стали. В то же время, в гистерезисных кривых, снятых экспериментальным путем, присутствуют обе составляющие, причем в динамике. Как калибровать расчетные кривые по результатам экспериментальных исследований непонятно.
Третий недостаток касается учета влияния на результаты моделирования магнитных потоков за пределами магнитопровода. Традиционно в моделях трансформатора, которые строятся на основе Т-образной схемы замещения (в том числе и в случае использования модели идеального трансформатора), в первичной и вторичной ветвях присутствуют постоянные по величине индуктивности рассеяния (на фиг. 1 – это элементы L1 и L2).
Данные индуктивности для трансформаторов рассчитываются или определяются экспериментально из опыта КЗ, в котором намагничивающие силы (НС) первичной и вторичной обмоток одинаковы по величине и противоположны по знаку. При этом магнитные поля обеих обмоток ослабляют друг друга так, что их общее поле за пределами магнитопровода сосредотачивается, главным образом, в главном канале между обмотками, который поэтому и называется каналом рассеяния.
Однако если использовать модель, представленную на фиг. 1, при моделировании произвольных режимов работы, то проблемы возникают даже при моделировании рема ХХ, так как в этом режиме НС вторичной обмотки равна нулю и ничего не ограничивает магнитный поток за пределами магнитопровода, создаваемый первичной обмоткой. При этом индуктивность L1, вычисленная для опыта ХХ оказывается на один-два порядка выше той же индуктивности, но рассчитанной из опыта КЗ. И если в режиме установившегося ХХ эта ошибка настолько мала, что ей можно пренебречь, то при расчете первого броска тока ХХ при включении трансформатора на ХХ в момент прохождения кривой напряжения u1(t) через 0, бросок тока, полученный на модели, представленной на фиг. 1, оказывается существенно завышенным, так как в данном режиме ток оказывается очень большим, магнитный поток рассеяния существенно возрастает и им уже нельзя пренебречь. То есть здесь даже в режиме ХХ индуктивность рассеяния играет значительную роль, но рассчитана она неверно, то есть исходя из условий, не соответствующих режиму ХХ (практически на два порядка).
Аналогичные ошибки возникают и при моделировании других переходных режимов, особенно в случае многообмоточных трансформаторов, в которых индуктивности рассеяния обмоток, рассчитанные или измеренные из опыта КЗ, для некоторых обмоток могут принимать отрицательные значения, что вообще противоречит физическому смыслу.
Технический результат предлагаемого способа заключается в создании цифровой модели трансформатора, калиброванной по результатам экспериментальных исследований реального устройства, способной выступать в качестве цифрового двойника данного реального трансформатора, позволяя имитировать его работу с большой точностью совпадения мгновенных токов и напряжений, полученных в результате моделирования произвольных режимов работы трансформатора, с реальными осциллограммами, полученными при испытании данного устройства. Созданный таким образом ЦД ОЭТ может использоваться для прогнозирования последствий нештатных ситуаций на данном конкретном устройстве (в частности, аварийных режимов, например, КЗ) или последствий эксплуатации данного устройства в нештатных режимах (например, в режиме перегрузки).
Технический результат достигается предлагаемым способом построения цифрового двойника реального однофазного электрического трансформатора, включающим построение имитационной модели устройства на основе Т-образной схемы замещения трансформатора с параллельным соединением элементов ветви намагничивания и модели идеального трансформатора. Проведение ее калибровки по результатам экспериментальных измерений на реальном устройстве, включающих измерение сопротивлений первичной и вторичной обмоток трансформатора на постоянном токе. Проведение двух опытов холостого хода, сначала при подаче напряжения с первичной стороны, потом со вторичной стороны трансформатора, и одного опыта короткого замыкания при подаче напряжения с первичной стороны трансформатора. По результатам опыта короткого замыкания рассчитывают коэффициент добавочных потерь трансформатора, отличающийся тем, что:
- в опытах холостого хода снимаются осциллограммы напряжения и тока обмотки, на которую подается напряжение, осциллограмма напряжения на разомкнутой обмотке с противоположной стороны трансформатора и осциллограмма напряжения на разомкнутой измерительной обмотке, состоящей из нескольких витков намотанных на верхнее ярмо трансформатора с П-образным сердечником или на боковое ярмо трансформатора с Ш-образным сердечником (после измерений данная обмотка удаляется);
- полученные осциллограммы очищают от высокочастотных шумов;
- по очищенным от шумов осциллограммам рассчитывают матрицу индуктивностей (взаимного влияния обмоток) по магнитным полям за пределами магнитопровода Ls, активное сопротивление ветви намагничивания Rµ и кривая намагничивания трансформатора в форме i0r(Ψ1), где i0r – намагничивающий ток трансформатора; Ψ1 – потокосцепление вторичной обмотки; расчет осуществляется в следующей последовательности:
• на очищенных от шумов осциллограммах выделяют период, соответствующий установившемуся процессу холостого хода;
• на выделенном периоде осуществляют расчет элементов матрицы индуктивностей по полям за пределами магнитопровода; расчет осуществляют по формулам:
 ,
,
где T – период; Ψσp(t) – мгновенное значение потокосцепления p-й обмотки с магнитным полем за пределами магнитопровода, создаваемое током iq, протекающим по q-й обмотке; Ψp(t) – мгновенное значение потокосцепления p-й обмотки с общим магнитным полем, создаваемым током iq; Ф0(t) – мгновенное значение магнитного потока в магнитопроводе; wp – количество витков в p-й обмотке,
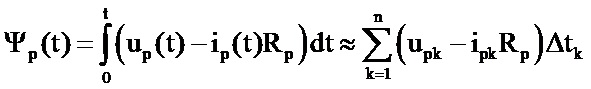 ;
;
где up(t) – мгновенное значение напряжения на p-й обмотке; ip – мгновенное значение тока в p-й обмотке (для разомкнутой обмотки ip = 0); Rp – активное сопротивление p-й обмотки;
• по осциллограммам u1(t) и тока i1(t) вычисляют мгновенную мощность по формуле pt = u1t . i1t, а затем строят кривую зависимости от времени мгновенной мощности; по данной кривой по формуле  , где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, вычисляют мощность магнитных потерь, по формуле
, где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, вычисляют мощность магнитных потерь, по формуле  , где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, действующее значение напряжения, а сопротивление ветви намагничивания Rµ рассчитывают по формуле:
, где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, действующее значение напряжения, а сопротивление ветви намагничивания Rµ рассчитывают по формуле: 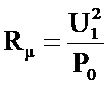 , где U1 – действующее значение напряжения, поданного на первичную обмотку, рассчитываемое по осциллограмме напряжения u1(t) по формуле
, где U1 – действующее значение напряжения, поданного на первичную обмотку, рассчитываемое по осциллограмме напряжения u1(t) по формуле
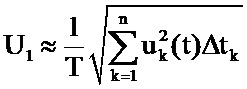 ;
;
• затем строится кривая электромагнитного гистерезиса, представленная на фиг. 9; при этом используется формула 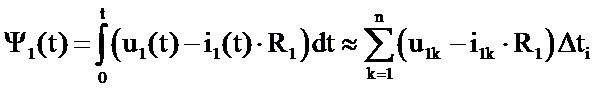 ;
;
• по данной гистерезисной кривой по (10) строится расчетная кривая реального трансформатора i0r(Ψ1);
- по найденному в опыте короткому замыканию коэффициенту добавочных потерь корректируют значения сопротивлений первичной и вторичной обмоток, измеренные на постоянном токе, что позволяет учесть в имитационной модели добавочные потери в трансформаторе; для этого сопротивления обмоток умножаются на коэффициент добавочных потерь;
- в электрическую схему замещения трансформатора вместо индуктивностей рассеяния L1 и L2 (см. фиг. 1) вносятся два управляемых источника тока is1 и is2 (см. фиг. 4), на управляющие входы которых подаются мгновенные значения токов первичной и вторичной обмоток, рассчитываемые с использованием обращенной матрицы индуктивностей по полям за пределами магнитопровода [Ls] (блок [Ls]^-1*u на фиг. 4);
- откорректированные значения сопротивлений R1 и R2 указывают в качестве номиналов элементов R1 и R2 имитационной модели (см. фиг. 4);
- кривую намагничивания i0r(Ψ1) задают в параметрах блока табличной зависимости i0r(Psi1) (см. фиг. 4).
Следовательно, технический результат достигается путем использования при создании ЦД ОЭТ матрицы индуктивной связи первичной и вторичной обмоток по магнитным полям за пределами магнитопровода, а также путем калибровки цифровой модели, основанной на анализе экспериментальных осциллограммам токов и напряжений в режиме ХХ и КЗ, по которым рассчитываются матрица индуктивностей по полям за пределами магнитопровода, активное сопротивление ветви намагничивания и реальная кривая намагничивания.
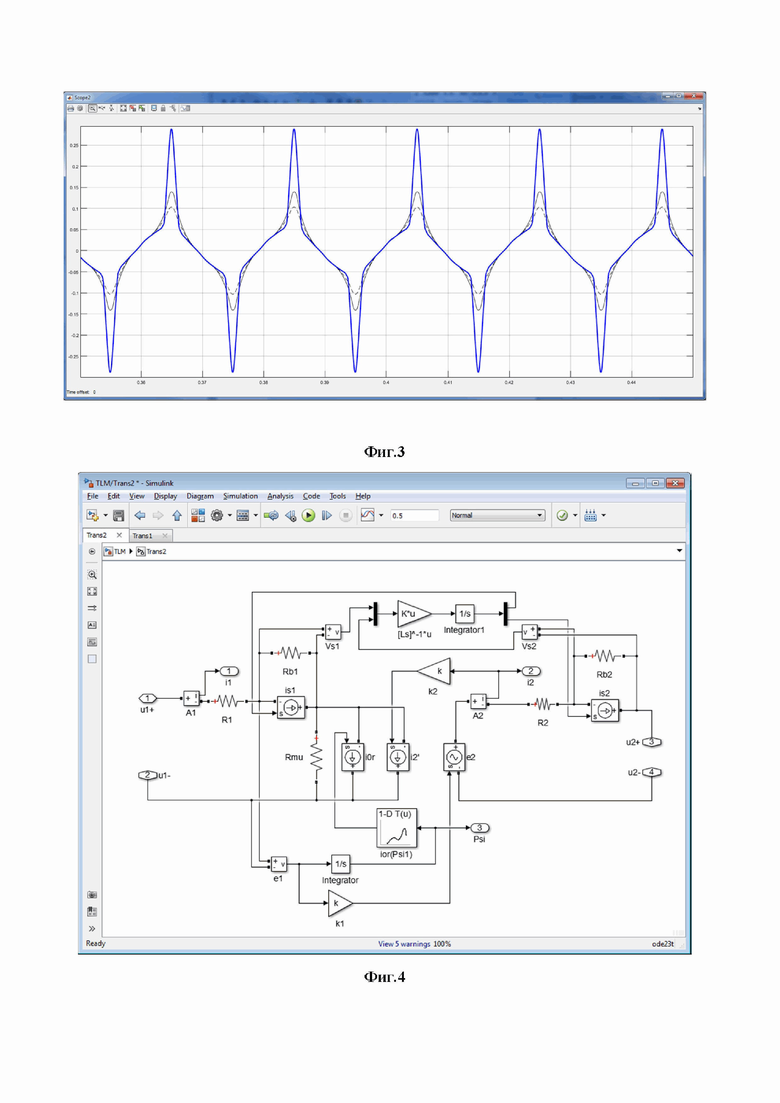
Предлагаемый способ поясняется схемами, где на фиг. 4 показана схема цифровой имитационной модели однофазного трансформатора, адаптированная к возможности калибровки по результатам испытаний на реальном устройстве, на фиг. 5 – осциллограммы первичного напряжения и тока однофазного трансформатора в режиме ХХ, на фиг. 6 – осциллограммы первичного напряжения и первичного тока в опыте ХХ на одном периоде в установившемся режиме, на фиг. 7 – отфильтрованные осциллограммы первичного напряжения и первичного тока, на фиг. 8 – кривая активной мощности однофазного трансформатора, на фиг. 9 – кривая электромагнитного гистерезиса и основная кривая намагничивания однофазного трансформатора, на фиг. 10 – результаты расчета включения однофазного трансформатора на нагрузку с использованием трех моделей переходных режимов.
В отличие от схемы, приведенной на фиг. 1, в схеме на фиг. 4 вместо индуктивностей рассеяния L1 и L2 используется электрическая схема замещения двух индуктивно связанных катушек, состоящая из двух управляемых источников тока, на управляющие входы которых подаются сигналы, вычисляемые по формуле
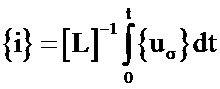 , (2)
, (2)
где 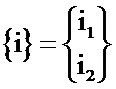 – матрица-столбец мгновенных токов в обмотках;
– матрица-столбец мгновенных токов в обмотках; 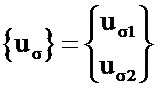 – матрица-столбец мгновенных падений напряжения на индуктивностях рассеяния;
– матрица-столбец мгновенных падений напряжения на индуктивностях рассеяния; 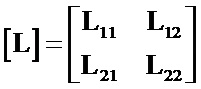 – матрица индуктивной связи между обмотками по потокам рассеяния (точнее по потокам за пределами магнитопровода).
– матрица индуктивной связи между обмотками по потокам рассеяния (точнее по потокам за пределами магнитопровода).
Данный прием позволяет учесть взаимное влияние обмоток по магнитным полям за пределами магнитопровода. Элементы этих матриц определяются экспериментальным путем из осциллограмм, снятых на реальном трансформаторе в двух опытах ХХ, когда напряжение подается поочередно на первичную и вторичную обмотки при разомкнутых противоположных обмотках. Расчет осуществляется по формуле
 , (3)
, (3)
где T – период; Ψσp(t) – мгновенное значение потокосцепления p-й обмотки с магнитным полем за пределами магнитопровода, создаваемое током iq, протекающим по q-й обмотке; Ψp(t) – мгновенное значение потокосцепления p-й обмотки с общим магнитным полем, создаваемым током iq; Ф0(t) – мгновенное значение магнитного потока в магнитопроводе; wp – количество витков в p-й обмотке.
Для расчета Lpq напряжение uq(t) подается на q-ю обмотку при разомкнутой p-й обмотке. Протекающий по q-й обмотке ток iq создает магнитное поле, которое сцепляется с обеими обмотками. Потокосцепление данного поля с p-й обмоткой определяется по формуле
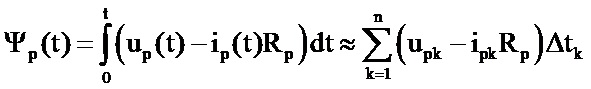 ; (4)
; (4)
где up(t) – мгновенное значение напряжения на p-й обмотке; ip – мгновенное значение тока в p-й обмотке (для разомкнутой обмотки ip = 0); Rp – активное сопротивление p-й обмотки.
Из общего потокосцепления p-й обмотки надо выделить вклад от потоков за пределами магнитопровода. Для этого общего потокосцепления p-й обмотки вычитаем потокосцепление с основным полем Ф0p = Ф0.wp. Для определения основного магнитного потока Ф0 используется вспомогательная измерительная обмотка, которая располагается либо на боковых ярмах трансформатора с Ш-образным сердечником, либо на верхнем ярме трансформатора с П-образным сердечником. При этом используется формула
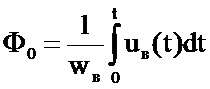 , (5)
, (5)
где uв(t) – мгновенное значение напряжения на вспомогательной обмотке; wв – число витков во вспомогательной обмотке.
Все мгновенные значения токов и напряжений определяются по осциллограммам, снятым на реальном устройстве.
Для расчета реальной кривой намагничивания трансформатора используем осциллограммы первичного напряжения u1(t) и первичного тока i1(t), снятые на реальном трансформаторе в режиме установившегося ХХ.
Рассмотрим данную методику на примере трансформатора ОСМ1-0,063ЗУЗ, осциллограммы тока и напряжения которого приведены на фиг. 5.
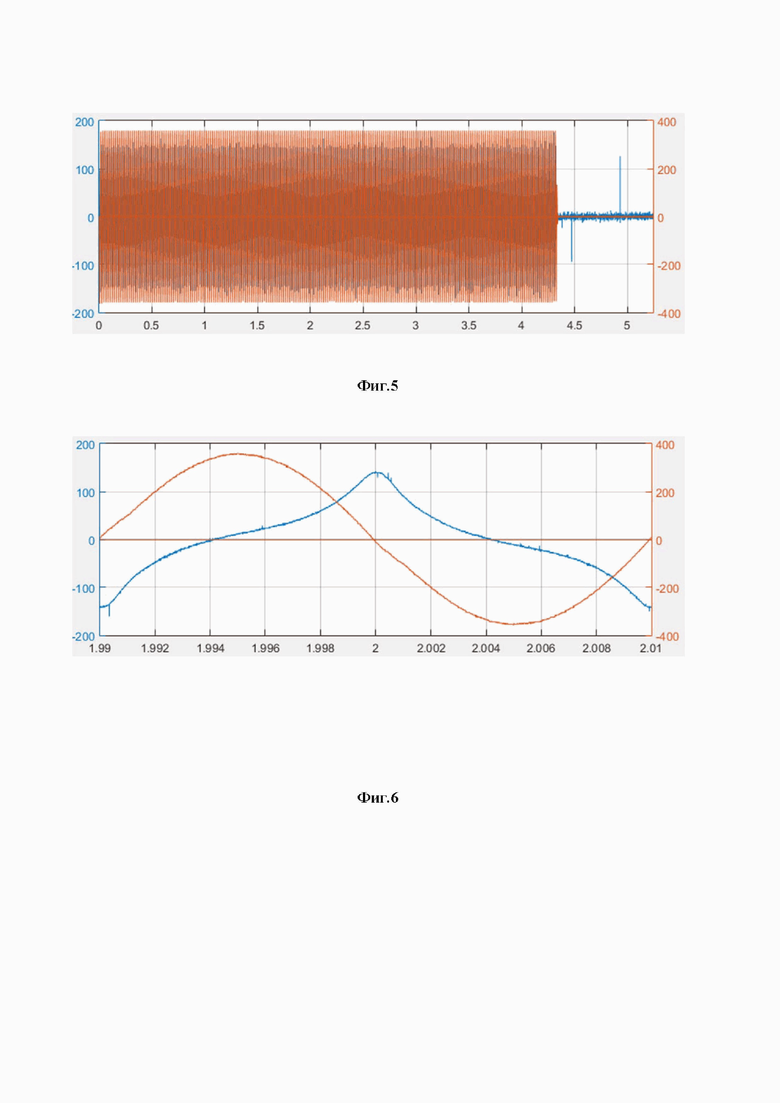
На фиг. 6 приведены осциллограммы первичного напряжения u1(t) и первичного тока i1(t) реального трансформатора на одном периоде в установившемся режиме.
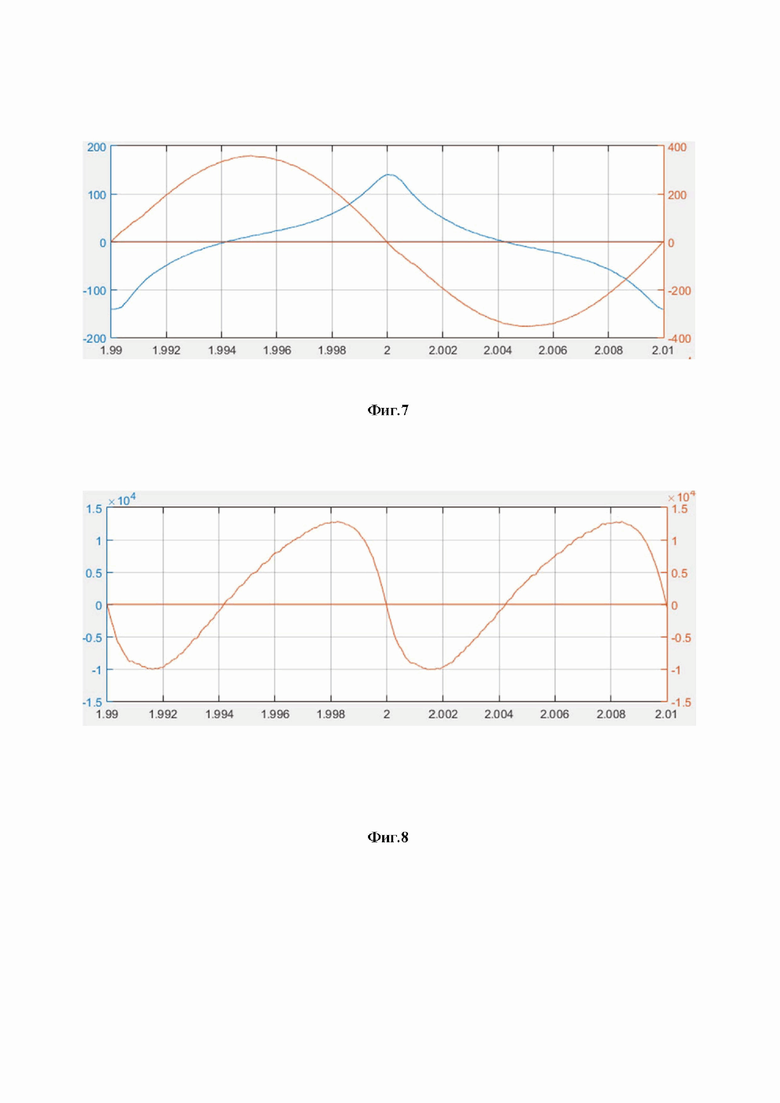
На фиг. 7 приведены эти же осциллограммы, но отфильтрованные от высокочастотных шумов.
На фиг. 8 приведены кривые зависимости от времени мощности магнитных потерь в сердечнике трансформатора, рассчитываемы по осциллограммам, приведенным на фиг. 7, по формуле
 , (6)
, (6)
где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями.
Сопротивление ветви намагничивания рассчитывается по формуле
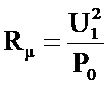 , (7)
, (7)
где U1 – действующее значение напряжения, поданного на первичную обмотку, рассчитываемое по осциллограмме напряжения u1(t) по формуле
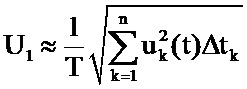 . (8)
. (8)
По отфильтрованной осциллограмме тока и напряжения (фиг. 7) рассчитывается кривая электромагнитного гистерезиса, представленная на фиг. 9.
Расчет мгновенных значений потокосцепления первичной обмотки при этом осуществляется по формуле
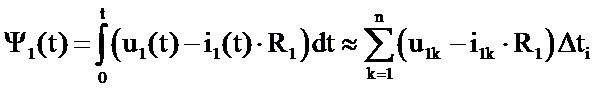 . (9)
. (9)
Расчет средней кривой намагничивания (см. фиг. 9) осуществляется для каждого i-го значения тока по формуле
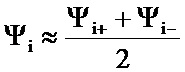 , (10)
, (10)
где 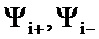 , - соответственно потокосцепления на восходящей и нисходящей ветвях кривой магнитного гистерезиса при i-м значении тока.
, - соответственно потокосцепления на восходящей и нисходящей ветвях кривой магнитного гистерезиса при i-м значении тока.
Средняя кривая намагничивания заводится в качестве параметров блока табличной зависимости i0r(Psi1) в модели, представленной на фиг. 4.
Результат расчета установившегося тока ХХ трансформатора ОСМ1-0,063ЗУЗ на модели, откалиброванной по осциллограммам реального трансформатора, приведен на фиг. 2 (кривая 3). Как отмечалось, данная кривая практически совпадает с реальной осциллограммой, представленной на фиг. 2 кривой 1. Как видно из сравнения кривых 1 и 2 на фиг. 2, кривая зависимости первичного тока от времени строится с учетом гистерезисных явлений (максимум кривой тока смещен относительно точек пересечения данной кривой горизонтальной оси времени). При этом не потребовалось вводить сложных коррекций модели, предлагаемых в [Casoria, S., P. Brunelle, and G. Sybille, «Hysteresis Modeling in the MATLAB/Power System Blockset», Electrimacs 2002, École de technologie supérieure, Montreal, 2002.; Frame, J.G., N. Mohan, and Tsu-huei Liu, «Hysteresis modeling in an Electro-Magnetic Transients Program», presented at the IEEE PES winter meeting, New York, January 31 to February 5, 1982.]. Достаточно вычисленного по (7) активного сопротивления ветви намагничивания. Следует отметить, что такой способ моделирования гистерезисных явлений позволяет учесть не только влияние на работу трансформатора собственно электромагнитного гистерезиса, но и влияние вихревых токов в магнитопроводе трансформатора. Данное допущение справедливо при моделировании трансформатора, работающего на постоянной частоте первичного напряжения.
Расчет процесса включения трансформатора ОСМ1-0,063ЗУЗ на нагрузку при нулевой фазе первичного напряжения (см. фиг. 10), осуществленный по схемам, приведенным на фиг. 1 (кривая 1) и на фиг. 4 (кривая 2), показал наличие существенного различия в расчетной величине первого броска первичного тока (порядка 42%). Примерно такое же различие наблюдается и в первом броске тока при включении трансформатора на ХХ. Как показало несколько численных исследований, в случае мощных трансформаторов расхождение в результатах моделирования, полученных на имитационных моделях с учетом и без учета взаимного влияния обмоток по полям за пределами магнитопровода может составлять 100% и более. Как отмечалось, это расхождение вызвано ошибкой в учете взаимного обмоток по полям за пределами магнитопровода. Предлагаемый способ построения ЦД ОЭТ позволяет учесть данное явление, что повышает точность имитации работы реального устройства в переходных режимах.
Способ осуществляют следующим образом:
В среде MatLab Simulink SimPowerSystems строится имитационная модель однофазного трансформатора, отличающаяся от аналогов способом моделирования потоков за пределами магнитопровода с использованием матрицы индуктивностей [Ls] (см. вверху на фиг. 4). Кроме того, в этой схеме напряжение e1 фиксируется не после индуктивности рассеяния, а до нее. Это позволяет использовать в качестве кривой намагничивания характеристику, снятую с реального трансформатора.
Традиционным способом непосредственно на реальном трансформаторе осуществляем опыт короткого замыкания (КЗ), из которого находим значения сопротивлений R1 и R2 имитационной модели, приведенной на фиг. 4.
На реальный трансформатора наматывается несколько витков измерительной обмотки. В трансформаторах с Ш-образным сердечником измерительная обмотка располагается на боковых ярмах, в трансформаторах с П-образным сердечником – на верхнем ярме трансформатора.
Определяем матрицу индуктивностей [Ls]. Для этого:
Проводим два опыта холостого хода (ХХ). В первом опыте номинальное напряжение подается на первичную обмотку при разомкнутой вторичной обмотке (p = 1) (данные осциллограммы имеют вид, представленный на фиг. 5.). Во втором опыте, наоборот, номинальное напряжение подается на вторичную обмотку при разомкнутой вторичной обмотке (p = 2). В обоих опытах снимаются осциллограммы напряжения up(t) и тока ip(t) в обмотке, подключенной к источнику напряжения, а также осциллограмма ЭДС uв(t), наводимой в измерительной обмотке.
Полученные осциллограммы оцифровываются (приводится к табличной форме).
Для каждой точки осциллограмм up(t) и тока ip(t) по формуле (4) на одном из периодов, соответствующем установившемуся процессу ХХ, рассчитывается зависимость от времени потокосцепления Ψp(t) p-й обмотки, подключенной к источнику напряжения.
Потом по (5) для этого же периода рассчитывается зависимость от времени основного потока Ф0(t) (для трансформатора с Ш-образным сердечником, полученные по (5) величины для каждого момента времени, надо умножить на 2). Элементы матрицы [Ls] рассчитываются по (3) по полученным зависимостям Ψp(t) и Ф0(t).
Определяем кривую намагничивания реального трансформатора. Для этого используем осциллограммы u1(t) и тока i1(t) (то есть при p = 1). Данные осциллограммы имеют вид, представленный на фиг. 5 (для реального трансформатора ОСМ1-0,063ЗУЗ).
На осциллограммах выделяем один период, соответствующий установившемуся процессу ХХ (фиг. 6).
С помощью фильтра очищаем данные осциллограммы от высокочастотных шумов (фиг. 7).
Для каждой точки (для каждого момента времени) осциллограмм u1(t) и тока i1(t) вычисляем мгновенную мощность по формуле pt = u1t . i1t, а затем строим кривую зависимости от времени мгновенной мощности (фиг. 8).
По данной кривой по формуле (6) вычисляем мощность магнитных потерь, по (8) – действующее значение напряжения и по (7) – сопротивление ветви намагничивания Rµ. Данное значение передается качестве параметра элемента Rmu в модель, приведенную на фиг. 4.
Затем по кривым, приведенным на фиг. 7 строится кривая электромагнитного гистерезиса, представленная на фиг. 9. При этом используется формула (9).
По данной гистерезисной кривой по (10) строится расчетная кривая реального трансформатора, которая поставляется в качестве параметра блока табличной зависимости i0r(Psi1) в модели, представленной на фиг. 4.
После этого процесс создания цифрового двойника реального однофазного трансформатора можно считать законченным.
Далее приводятся результаты расчета трансформатора на данной модели.
Таким образом, предлагаемый способ создания цифровых двойников электрических трансформаторов позволяет построить цифрового (виртуального) двойника реального устройства, способного функционировать в виртуальной реальности подобно реальному устройству с учетом конкретных особенностей его конструкции как в установившихся, так и переходных и даже в аварийных режимах, позволяя прогнозировать состояние реального трансформатора, особенно после критических событий (КЗ, перегрузок и т.п.). Функционал данного цифрового двойника может эволюционно расширяться путем добавления в него алгоритмов моделирования различных физических процессов (тепловых, механических, шумов и т.п.).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РЕЛЕЙНОЙ ЗАЩИТЫ ТРАНСФОРМАТОРА | 2016 |
|
RU2643779C1 |
| СПОСОБ РЕЛЕЙНОЙ ЗАЩИТЫ ТРЕХФАЗНОГО ТРАНСФОРМАТОРА | 2017 |
|
RU2655920C1 |
| СПОСОБ КОМПЕНСАЦИИ ПОГРЕШНОСТИ ТРАНСФОРМАТОРА ТОКА | 2012 |
|
RU2526834C2 |
| Способ фильтрации тока намагничивания и воспроизведения первичного тока измерительных трансформаторов тока | 2019 |
|
RU2708228C1 |
| Способ фильтрации тока намагничивания и воспроизведения первичного напряжения измерительных двухобмоточных трансформаторов напряжения | 2019 |
|
RU2728510C1 |
| ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТЫ | 1994 |
|
RU2077110C1 |
| Способ уменьшения погрешности и увеличения диапазона точного определения первичного сигнала трансформатора | 2017 |
|
RU2646863C1 |
| Способ фильтрации тока намагничивания и воспроизведения вторичных токов многообмоточных силовых трансформаторов | 2017 |
|
RU2684169C2 |
| СПОСОБ ФИЛЬТРАЦИИ ТОКА НАМАГНИЧИВАНИЯ И ВОСПРОИЗВЕДЕНИЯ ВТОРИЧНОГО ТОКА СИЛОВЫХ И ИЗМЕРИТЕЛЬНЫХ ТРАНСФОРМАТОРОВ НАПРЯЖЕНИЯ | 2015 |
|
RU2586115C1 |
| Устройство для формирования тока проверки релейной защиты | 1981 |
|
SU1014061A1 |

Изобретение относится к области электротехники. Технический результат заключается в обеспечении возможности имитировать работу трансформатора с большой точностью совпадения мгновенных токов и напряжений, полученных в результате моделирования произвольных режимов работы трансформатора с реальными осциллограммами. Такой результат достигается тем, что при создании цифрового двойника однофазного электрического трансформатора используют матрицы индуктивной связи первичной и вторичной обмоток по магнитным полям за пределами магнитопровода, производят калибровку цифровой модели, основанную на анализе экспериментальных осциллограммам токов и напряжений в режиме холостого хода (ХХ) и короткого замыкания (КЗ), по которым рассчитываются матрица индуктивностей по полям за пределами магнитопровода, активное сопротивление ветви намагничивания и реальная кривая намагничивания. 10 ил.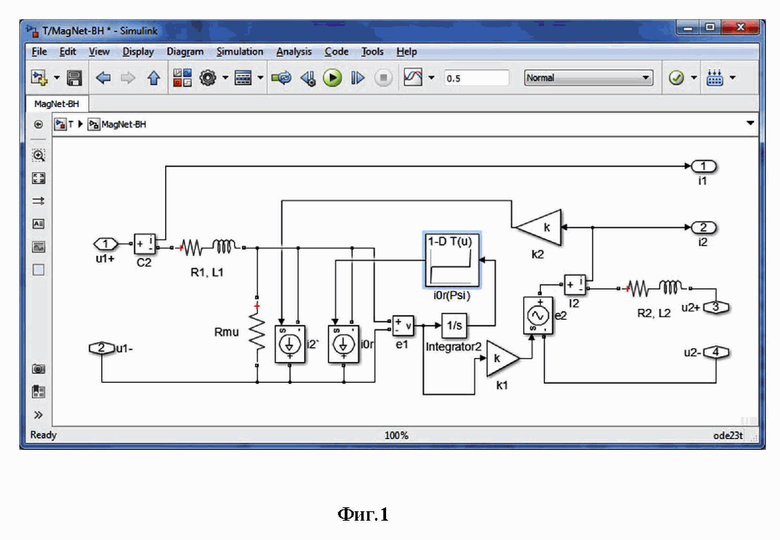
Способ построения цифрового двойника реального однофазного электрического трансформатора, включающий построение имитационной модели устройства на основе Т-образной схемы замещения трансформатора с параллельным соединением элементов ветви намагничивания и модели идеального трансформатора, а также проведение ее калибровки по результатам экспериментальных измерений на реальном устройстве, включающих измерение сопротивлений первичной и вторичной обмоток трансформатора на постоянном токе, проведение двух опытов холостого хода, сначала при подаче напряжения с первичной стороны, потом со вторичной стороны трансформатора, и одного опыта короткого замыкания при подаче напряжения с первичной стороны трансформатора; по результатам опыта короткого замыкания рассчитывают коэффициент добавочных потерь трансформатора, отличающийся тем, что:
- в опытах холостого хода снимаются осциллограммы напряжения и тока обмотки, на которую подается напряжение, осциллограмма напряжения на разомкнутой обмотке с противоположной стороны трансформатора и осциллограмма напряжения на разомкнутой измерительной обмотке, состоящей из нескольких витков намотанных на верхнее ярмо трансформатора с П-образным сердечником или на боковое ярмо трансформатора с Ш-образным сердечником (после измерений данная обмотка удаляется);
- полученные осциллограммы очищают от высокочастотных шумов;
- по очищенным от шумов осциллограммам рассчитывают матрицу индуктивностей (взаимного влияния обмоток) по магнитным полям за пределами магнитопровода Ls, активное сопротивление ветви намагничивания Rμ и кривая намагничивания трансформатора в форме i0r(Ψ1), где i0r – намагничивающий ток трансформатора; Ψ1 – потокосцепление вторичной обмотки; расчет осуществляется в следующей последовательности:
• на очищенных от шумов осциллограммах выделяют период, соответствующий установившемуся процессу холостого хода;
• на выделенном периоде осуществляют расчет элементов матрицы индуктивностей по полям за пределами магнитопровода; расчет осуществляют по формулам:
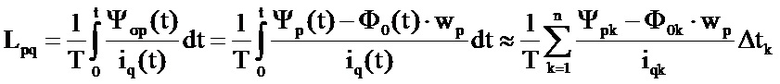 ,
,
где T – период; Ψσp(t) – мгновенное значение потокосцепления p-й обмотки с магнитным полем за пределами магнитопровода, создаваемое током iq, протекающим по q-й обмотке; Ψp(t) – мгновенное значение потокосцепления p-й обмотки с общим магнитным полем, создаваемым током iq; Ф0(t) – мгновенное значение магнитного потока в магнитопроводе; wp – количество витков в p-й обмотке,
и 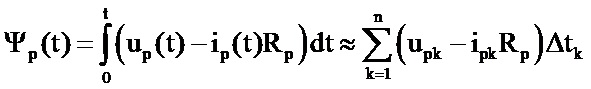 ;
;
где up(t) – мгновенное значение напряжения на p-й обмотке; ip – мгновенное значение тока в p-й обмотке (для разомкнутой обмотки ip = 0); Rp – активное сопротивление p-й обмотки;
• по осциллограммам u1(t) и тока i1(t) вычисляют мгновенную мощность по формуле pt = u1t .⋅ i1t, а затем строят кривую зависимости от времени мгновенной мощности; по данной кривой по формуле 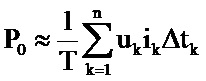 , где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, вычисляют мощность магнитных потерь, по формуле
, где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, вычисляют мощность магнитных потерь, по формуле 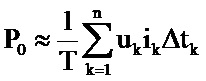 , где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, действующее значение напряжения, а сопротивление ветви намагничивания Rμ рассчитывают по формуле:
, где T – период; n – количество точек осциллограммы на периоде; Δtk – k-й интервал времени меду двумя измерениями, действующее значение напряжения, а сопротивление ветви намагничивания Rμ рассчитывают по формуле: 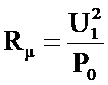 , где U1 – действующее значение напряжения, поданного на первичную обмотку, рассчитываемое по осциллограмме напряжения u1(t) по формуле
, где U1 – действующее значение напряжения, поданного на первичную обмотку, рассчитываемое по осциллограмме напряжения u1(t) по формуле
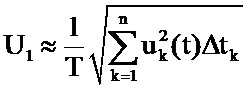 ;
;
• затем строят кривую электромагнитного гистерезиса, при этом используют формулу  ;
;
• по данной гистерезисной кривой строится расчетная кривая реального трансформатора i0r(Ψ1) по формуле  , где
, где 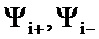 - соответственно потокосцепления на восходящей и нисходящей ветвях кривой магнитного гистерезиса при i-м значении тока;
- соответственно потокосцепления на восходящей и нисходящей ветвях кривой магнитного гистерезиса при i-м значении тока;
- по найденному в опыте короткому замыканию коэффициенту добавочных потерь корректируют значения сопротивлений первичной и вторичной обмоток, измеренные на постоянном токе, для чего сопротивления обмоток умножают на коэффициент добавочных потерь;
- в электрическую схему замещения трансформатора вносят два управляемых источника тока is1 и is2, на управляющие входы которых подают мгновенные значения токов первичной и вторичной обмоток, рассчитываемые с использованием обращенной матрицы индуктивностей по полям за пределами магнитопровода [Ls];
- откорректированные значения сопротивлений R1 и R2 указывают в качестве номиналов элементов R1 и R2 имитационной модели;
- кривую намагничивания i0r(Ψ1) задают в параметрах блока табличной зависимости i0r(Psi1).
| Станок для придания концам круглых радиаторных трубок шестигранного сечения | 1924 |
|
SU2019A1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| CN 110243834 A, 17.09.2019 | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ ТРЕХФАЗНОГО МНОГООБМОТОЧНОГО ТРАНСФОРМАТОРА | 2011 |
|
RU2479025C1 |
Авторы
Даты
2023-07-24—Публикация
2022-12-04—Подача