Изобретение относится к экспериментальной механике и предназначено для определения существенно неоднородных высокоградиентных двумерных полей остаточных напряжений (ОН), возникающих при изготовлении плоских элементов машин и конструкций, например, с применением сварки различного типа. Технический результат заключается в существенном уменьшении трудоемкости экспериментального исследования при обеспечении высокой точности результатов определения остаточных напряжений.
Наиболее близким техническим решением, которые можно рассматривать в качестве прототипа предлагаемого способа, является способ определения неоднородных полей остаточных напряжений в плоских деталях с помощью метода последовательно наращиваемой трещины (Vaidyanathan S., Finnie I., Determination of Residual Stresses from Stress Intensity Factor Measurements // J. Basic Engng. 1971. Vol. 93. P. 242-246), согласно которому во внутренней, удаленной от границ плоской детали, где имеется поле ОН, дискретными шагами наращивают разрез-трещину; на каждом шаге проводят измерения полей напряжений или перемещений в зоне вершины трещины, по которым определяются величины коэффициентов интенсивности напряжений нормального отрыва (KI) и поперечного сдвига (KII) для каждого i-го шага трещины (KI,i и KII,i); по найденным таким образом экспериментальным зависимостям KI(x) и KII(х) определяются искомые распределения остаточных напряжений σу(х) и τху(х) вдоль отрезка линии разреза-трещины (у=0, х0≤х≤xn) на основе соотношений
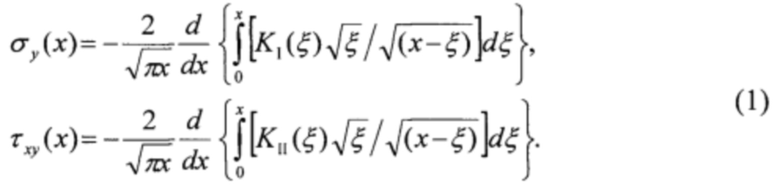
Из соотношений (1) следует корректность постановки задачи расчета остаточных напряжений на основе данных эксперимента, что обеспечивает устойчивость расчета остаточных напряжений к погрешностям исходных экспериментальных данных. Существенным недостатком такого подхода, позволяющего обеспечить высокую точность определения неоднородного высокоградиентного (вплоть до разрывного) распределения ОН, является его высокая трудоемкость, так как не каждом шаге приращения длины трещины требуется определение величин KI(x) и KII(х) на основе математической обработки полей напряжений или перемещений в зоне вершины трещины с использованием интерференционно-оптических методов (И.А. Разумовский. Интерференционно-оптические методы механики деформируемого твердого тела. М.: Издательство МГТУ им. Н.Э. Баумана. 2007. 234 с).
Предлагаемый способ определения неоднородного поля включает в себя установку исследуемого объекта (элемента конструкции или образца) в оптическую схему спекл-интерферометра, регистрацию спектр-структуры на поверхности объекта в исходном состоянии высокоразрешающей цифровой видеокамерой, его удаление из оптической схемы интерферометра, создание в нем единственного узкого разреза-трещины, его возвращение в исходное положение в оптической схеме интерферометра, регистрацию спектр-структуры на его деформированной поверхности, визуализацию картин интерференционных полос путем численного вычитания двух зарегистрированных оцифрованных спекл-структур, определение полей приращений перемещений, вычисление компонент ОН, которые имели место на берегах разреза-трещины путем математической обработки полей приращений напряжений с использованием специализированной программы, разработанной на основе теоретического решения задачи теории упругости о напряженно-деформированном состоянии в пластине неограниченных размеров с внутренней трещиной, к берегам которой приложены произвольные нормальные и касательные напряжения и τху.
Техническим результатом предлагаемого изобретения является существенное уменьшение объема экспериментов при сохранении высокой точности определения неоднородных распределений остаточных напряжений в исследуемых образцах деталей и конструкций.
Технический результат достигается тем, что предлагаемый способ определения неоднородных полей остаточных напряжений в плоских деталях включает в себя совокупность следующих действий: установку исследуемого образца в схему оптического спектр-интерферометра, проведение регистрации исходного состояния спектр-структуры на его поверхности с помощью высокоразрешающей цифровой видеокамеры. После этого проводится регистрации состояния образца и его удаление из оптической схемы, далее создают в нем узкий разрез в виде трещины и возвращают образец в исходное положение в оптической схеме интерферометра, после чего производят вторую регистрацию спектр-структуры его деформированной поверхности и визуализацию полученной картины интерференционных полос путем численного вычитания двух зарегистрированных оцифрованных спектр-структур, определении полей приращений перемещений, по которым вычисляют компоненты остаточных напряжений, которые имели место на берегах разреза-трещины. Далее путем математической обработки полей приращений перемещений с использованием решения задачи теории упругости о напряженно-деформированном состоянии в пластине неограниченных размеров с внутренней трещиной, к берегам которой приложены произвольные нормальные и касательные напряжения, параметры которых вычисляют на основе главного вектора сил и момента, приложенных к дуге ΔГ контура трещины по формулам
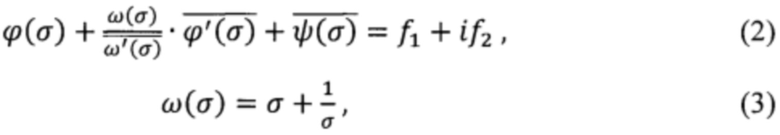
где ϕ(σ), ψ(σ) - аналитические функции - комплексные потенциалы Мусхелишвили; ω(σ) - функция, конформно отображающая контур выреза на окружность; σ - координата точки в комплексном виде; ƒ1+iƒ2=i∫(Xn+iYn)ds+С - функции, определяющие нагрузки Xn, Yn, на контуре трещины Г, которые являются искомыми остаточными напряжениями; ds - элемент дуги контура выреза; С - константа; 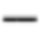 - символ комплексного сопряжения; ' - символ производной функции.
- символ комплексного сопряжения; ' - символ производной функции.
Связь между функциями напряжений ϕ(σ), ψ(σ) и определяемыми экспериментально компонентами вектора перемещений u и v выражается соотношением
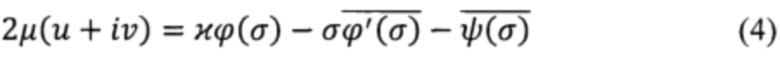
где u и v - компоненты тангенциальных перемещений; 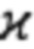 - параметр упругости материала, определяемый как
- параметр упругости материала, определяемый как 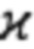 =(λ*+3μ)/(λ*+μ),λ*=2λμ/(λ+2μ); где λ* - первый параметр Ламе для обобщенного плоского напряженного состояния; λ и \μ - первый и второй параметры Ламе: λ=vE/(1+v)(1-2v); μi=E/2(1+v); E - модуль Юнга, v - коэффициент Пуассона
=(λ*+3μ)/(λ*+μ),λ*=2λμ/(λ+2μ); где λ* - первый параметр Ламе для обобщенного плоского напряженного состояния; λ и \μ - первый и второй параметры Ламе: λ=vE/(1+v)(1-2v); μi=E/2(1+v); E - модуль Юнга, v - коэффициент Пуассона
В отличие от прототипа предлагаемый способ требует создания в исследуемом объекта единственного прямолинейного разреза-трещины, что во много раз сокращает общую трудоемкость эксперимента. Процедура расчета распределения остаточных напряжений путем математической обработки полей деформаций (напряжений) заключается в следующем. В качестве основного соотношения используется общее решение плоской задачи теории упругости для пластины неограниченных размеров с вырезом произвольной формы, на контуре которого действуют произвольные нагрузки, полученное Н.И. Мусхелишвили ([1], Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 708 с.). Это соотношение имеет вид
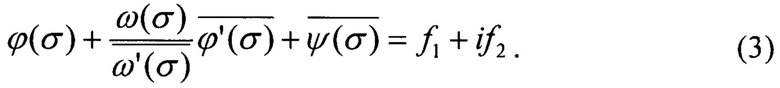
Здесь ϕ, ψ - комплексные потенциалы (функции напряжений); z=ω(ς) - аналитическая функция, конформно отображающая контур г на комплексной плоскости z=x+iy=|z|eiθ на окружность |ς|=1 на комплексной плоскости ς=ξ+iη; θ - полярный угол точки окружности |ς|=1;; ƒ1+iƒ2 - функции нагрузки на контуре, причем 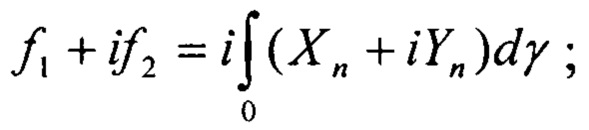 Xn, Yn - значения компонент внешних нагрузок на контуре г (фиг. 2); (…) и
Xn, Yn - значения компонент внешних нагрузок на контуре г (фиг. 2); (…) и 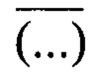 обозначает комплексно сопряженные функции.
обозначает комплексно сопряженные функции.
В случае использования в качестве индикатора остаточных напряжений трещины-выреза (фиг. 3) функция, конформно отображающая контур г на окружность, имеет следующий вид

Для решения соответствующей граничной задачи используется представление функций ϕ(…) и ψ(…)в виде степенных рядов [1]
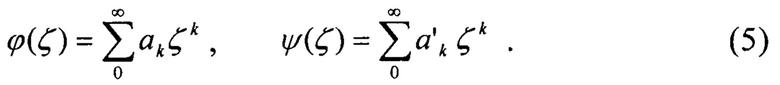
Функции конформного отображения ω(σ) и нагрузки ƒ1+ƒ2, действующие на контуре Г (искомые остаточные напряжения) представляются в следующем виде


Подставляя выражения (4) - (6) в формулу (2), и приравнивая коэффициенты при υm(m=1,2,…), получаем систему линейных уравнений для отображения границы выреза
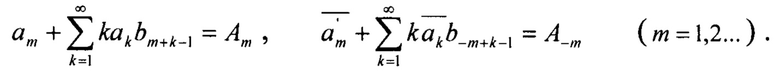
В результате преобразований получается система линейных уравнений вида

где [С] - матрица коэффициентов, 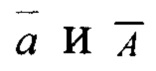 векторы коэффициентов разложения ϕ(…), ψ(…) и ƒ1+iƒ2.
векторы коэффициентов разложения ϕ(…), ψ(…) и ƒ1+iƒ2.
Найденные таким образом функции нагрузки, приложенной к контуру-вырезу ƒ1+iƒ2 являются искомыми распределения остаточных напряжений. Искомые функции отыскиваются в виде соответствующих разложений в ряды (4-6), и задача их определения сводится к нахождению коэффициентов их разложения в ряды указанного типа.
Корректность задачи определения остаточных напряжений на основе экспериментально полученных полей деформаций (напряжений) обеспечивается использованием используемых аналитических соотношений, связывающих экспериментальные данные с искомыми значениями на контуре выреза, возможностью оптимизации соответствующих расчетных процедур, а также возможностью обработки значительных массивов экспериментальной информации. При этом связь между остаточными напряжениями и деформациями определяется законом Гука.
Трудозатраты на проведение экспериментального исследования неоднородных полей остаточных напряжений данным методом значительно (во много раз) меньше, чем в методе последовательно наращиваемой трещины.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения коэффициентов интенсивности напряжений для трещин | 2017 |
|
RU2667316C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ | 2014 |
|
RU2574231C1 |
| СПОСОБ ОЦЕНКИ ПРОЧНОСТИ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ | 1999 |
|
RU2186361C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА, ВЫЗВАННЫХ ВОЛНИСТОСТЬЮ ПОВЕРХНОСТЕЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680615C1 |
| Устройство формирования фазового сдвига в оптическом диапазоне | 2018 |
|
RU2697900C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ ДЛЯ ТРЕЩИНЫ В КОНСТРУКЦИИ | 2021 |
|
RU2773260C1 |
| СПОСОБ ЛАЗЕРНОГО ГЕТЕРОДИННОГО ПРИЕМА ИЗЛУЧЕНИЙ | 2007 |
|
RU2349930C1 |
| Способ определения параметров взволнованной водной поверхности в инфракрасном диапазоне | 2017 |
|
RU2651625C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАБЕГА ФАЗЫ МОНОХРОМАТИЧЕСКОЙ ПОВЕРХНОСТНОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ИНФРАКРАСНОГО ДИАПАЗОНА | 2012 |
|
RU2491522C1 |
| СПОСОБ ВИЗУАЛИЗАЦИИ ПОЛЕЙ ФАЗОВОЙ ОПТИЧЕСКОЙ ПЛОТНОСТИ В ГАЗОВЫХ И КОНДЕНСИРОВАННЫХ СРЕДАХ | 2018 |
|
RU2681672C1 |
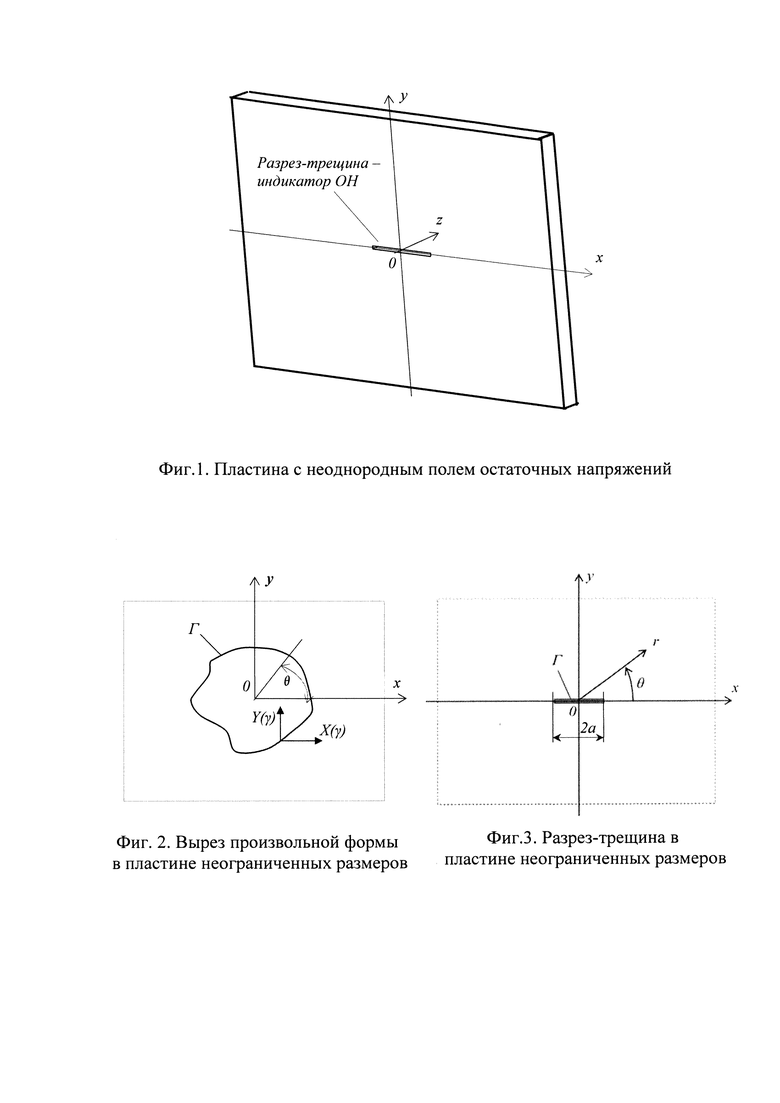
Изобретение относится к области экспериментальной механики и касается способа определения неоднородных полей остаточных напряжений в плоских деталях. Способ заключается в установке исследуемого образца в схему оптического спектр-интерферометра, проведении регистрации исходного состояния спектр-структуры на его поверхности с помощью высокоразрешающей цифровой видеокамеры. Затем в образце создают узкий разрез в виде трещины, после чего производят вторую регистрацию спектр-структуры его деформированной поверхности и визуализацию полученной картины интерференционных полос путем численного вычитания двух зарегистрированных оцифрованных спектр-структур. Далее определяют поля приращений перемещений, по которым вычисляют компоненты остаточных напряжений, которые имели место на берегах разреза-трещины, путем математической обработки полей приращений перемещений с использованием решения задачи теории упругости о напряженно-деформированном состоянии в пластине неограниченных размеров с внутренней трещиной, к берегам которой приложены произвольные нормальные и касательные напряжения, параметры которых вычисляют на основе главного вектора сил и момента, приложенных к дуге ΔГ контура трещины. Технический результат заключается в уменьшении объема экспериментов при сохранении высокой точности. 3 ил.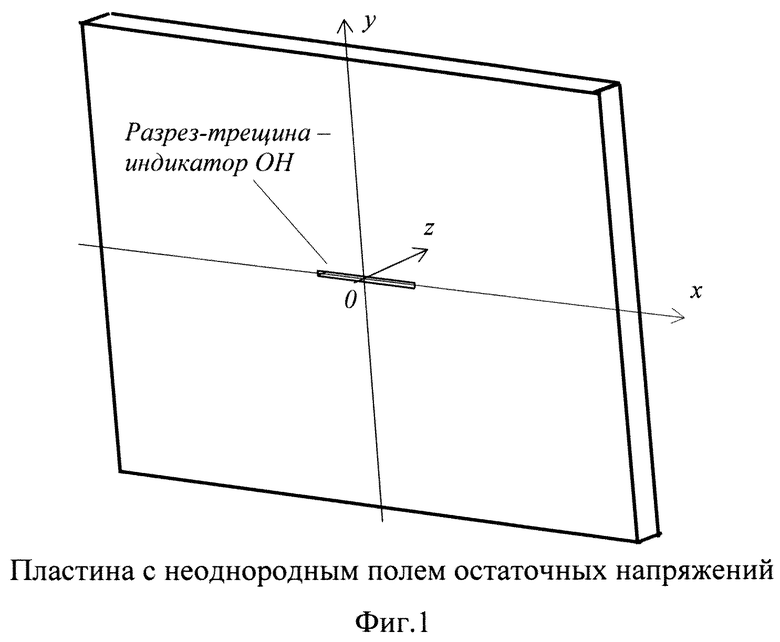
Способ определения неоднородных полей остаточных напряжений в плоских деталях, заключающийся в установке исследуемого образца в схему оптического спектр-интерферометра, проведении регистрации исходного состояния спектр-структуры на его поверхности с помощью высокоразрешающей цифровой видеокамеры, отличающийся тем, что после регистрации образец удаляют из оптической схемы, создают в нем узкий разрез в виде трещины и возвращают образец в исходное положение в оптической схеме интерферометра, после чего производят вторую регистрацию спектр-структуры его деформированной поверхности и визуализацию полученной картины интерференционных полос путем численного вычитания двух зарегистрированных оцифрованных спектр-структур, определении полей приращений перемещений, по которым вычисляют компоненты остаточных напряжений, которые имели место на берегах разреза-трещины, путем математической обработки полей приращений перемещений с использованием решения задачи теории упругости о напряженно-деформированном состоянии в пластине неограниченных размеров с внутренней трещиной, к берегам которой приложены произвольные нормальные и касательные напряжения, параметры которых вычисляют на основе главного вектора сил и момента, приложенных к дуге ΔГ контура трещины по формулам
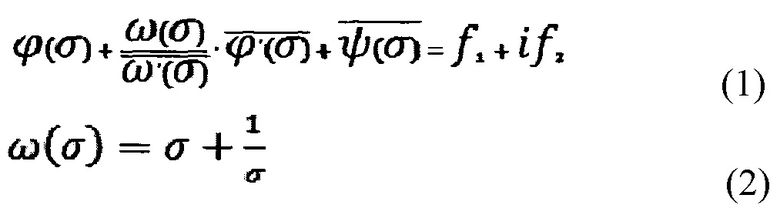
где ϕ(σ), ψ(σ) - аналитические функции - комплексные потенциалы Мусхелишвили;
ω(σ) - функция, конформно отображающая контур выреза на окружность;
σ - координата точки в комплексном виде;
ƒ1+iƒ2=i∫(Xn+iYn)ds+С - функции, определяющие нагрузки Xn, Yn, на контуре трещины Г, которые являются искомыми остаточными напряжениями;
ds - элемент дуги контура выреза;
С - константа;
 - символ комплексного сопряжения; ' - символ производной функции, при этом связь между функциями напряжений ϕ(σ), ψ(σ) и определяемыми экспериментально компонентами вектора перемещений u и v выражается соотношением
- символ комплексного сопряжения; ' - символ производной функции, при этом связь между функциями напряжений ϕ(σ), ψ(σ) и определяемыми экспериментально компонентами вектора перемещений u и v выражается соотношением
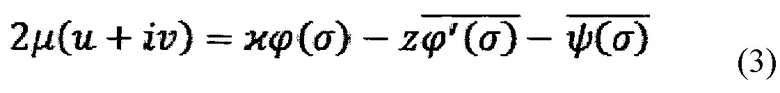
где u и v - компоненты тангенциальных перемещений,
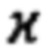 - параметр упругости материала, определяемый как
- параметр упругости материала, определяемый как
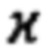 =(λ*+3μ)/(λ*+μ),λ*=2λμ/(λ+2μ),
=(λ*+3μ)/(λ*+μ),λ*=2λμ/(λ+2μ),
где λ* - первый параметр Ламе для обобщенного плоского напряженного состояния,
λ и μ - первый и второй параметры Ламе:
λ=vE/(1+v)(1-2v); μ=E/2(1+v);
E - модуль Юнга,
v - коэффициент Пуассона.
| Vaidyanathan S., Finnie I | |||
| "Determination of Residual Stresses from Stress Intensity Factor Measurements", JOURNAL OF BASIC ENGINEERING, т | |||
| Домовый номерной фонарь, служащий одновременно для указания названия улицы и номера дома и для освещения прилежащего участка улицы | 1917 |
|
SU93A1 |
| Металлические подъемные леса | 1921 |
|
SU242A1 |
| С.М | |||
| Усов и др | |||
| "Исследование полей остаточных напряжений с использованием трещин-индикаторов и метода электронной спекл-интерферометрии", ЗАВОДСКАЯ ЛАБОРАТОРИЯ | |||
| ДИАГНОСТИКА | |||
Авторы
Даты
2024-01-11—Публикация
2022-10-11—Подача