Изобретение относится к области экспериментальной механики и предназначено для определения коэффициентов интенсивности напряжений (КИН) для трещин при воздействии внешних и, особенно, остаточных напряжений, что необходимо для повышения эксплуатационного ресурса и надежности элементов авиационных конструкций за счет учета эволюции параметров механики разрушения вследствие циклического нагружения.
Известен ряд практически идентичных способов определения КИН для трещин в поле внешних напряжений на основе измерения полей перемещений в окрестности вершины трещины, согласно которым образец в виде пластины прямоугольной формы с начальной трещиной закрепляют в нагружающем устройстве (чаще всего в испытательной машине), монтируют оптическую схему электронного (цифрового) спекл-интерферометра, нагружают образец начальным усилием, регистрируют распределение фазы отраженной волны, соответствующее состоянию поверхности образца в исходном состоянии, нагружают образец конечным усилием, регистрируют распределение фазы отраженной волны, соответствующее деформированной поверхности образца вследствие увеличения нагрузки на образец с трещиной, получают распределение фаз отраженной волны, соответствующее разнице двух состояний, измеряют значения фазы этой волны для N точек (100≤N≤500) в окрестности вершины трещины, преобразуют значения фазы волны во всех точках, чтобы получить величины компонент тангенциальных перемещений в направлении линии трещины u и в перпендикулярном направлении ν, выбирают теоретическую модель, которая задает соотношения между измеренными перемещениями и силовыми параметрами линейной механики разрушения в окрестности вершины трещины, определяют величину КИН путем решения переопределенной системы алгебраических уравнений на основе метода наименьших квадратов (Moore A.J., Tyrer J.R. The evaluation of fracture mechanics parameters from electronic speckle pattern interferometric fringe patterns // Optics and lasers in Engineering. - 1993. V. 19, №4-5. - P. 325-336; Shternlikht A.,  F.A., Lopez-Crespo P., Withers P.J., Patterson E.A. Mixed Mode (KI+KII) Stress Intensity Factor Measurement by Electronic Speckle Pattern Interferometry and Image Correlation // Applied Mechanics Materials. - 2004. V. 1-2. - P. 107-112; Yoneyama S., Ogawa Т., Kobayashi Y. Evaluating mixed-mode stress intensity factors from full-field displacement fields obtained by optical methods // Engineering Fracture Mechanics. - 2007. V. 74, №9. - P. 1399-1412; Vasco-Olmo J.M., James M.N., Christopher C.J., Patterson E.A.,
F.A., Lopez-Crespo P., Withers P.J., Patterson E.A. Mixed Mode (KI+KII) Stress Intensity Factor Measurement by Electronic Speckle Pattern Interferometry and Image Correlation // Applied Mechanics Materials. - 2004. V. 1-2. - P. 107-112; Yoneyama S., Ogawa Т., Kobayashi Y. Evaluating mixed-mode stress intensity factors from full-field displacement fields obtained by optical methods // Engineering Fracture Mechanics. - 2007. V. 74, №9. - P. 1399-1412; Vasco-Olmo J.M., James M.N., Christopher C.J., Patterson E.A.,  F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding // Fatigue & Fracture of Engineering Materials & Structures. - 2016. V. 39, №8. - P. 969-981; Vasco-Olmo J.M.,
F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding // Fatigue & Fracture of Engineering Materials & Structures. - 2016. V. 39, №8. - P. 969-981; Vasco-Olmo J.M.,  F.A., Patterson E.A. Experimental evaluation of shielding effect on growing fatigue cracks under overloads using ESPI // International Journal of Fatigue. - 2016. V. 83. №2. - P. 117-126).
F.A., Patterson E.A. Experimental evaluation of shielding effect on growing fatigue cracks under overloads using ESPI // International Journal of Fatigue. - 2016. V. 83. №2. - P. 117-126).
Главным техническим недостатком подобного подхода является сложность оптической схемы интерферометра, которая требует освещения исследуемой плоской поверхности двумя симметричными по отношению к нормали к ее поверхности освещающими пучками, причем в один из этих пучков необходимо включать модулятор световой волны, обеспечивающий автоматическое измерение фазы рассеянной поверхностью объекта волны и последующее определение тангенциальных компонент перемещений (Bova М., Bruno L., Poggialini A. Low-cost speckle interferometry for measuring 3D deformation fields: Hardware and software // Optics and Lasers in Engineering. - 2010. V. 48, №1. - P. 96-106). Использование метода фазового сдвига освещающей волны ограничивает количество точек измерений, которое, обычно, не превышает несколько сотен. Кроме того, метод электронной спекл-интерферометрии требует освещения исследуемой поверхности лазерным излучением. Это приводит к высокой чувствительности интерферометра к тангенциальным компонентам перемещений без возможности ее регулировать, что не всегда является положительным моментом при определении величин КИН.
В последние годы наличие высокоразрешающих интерференционных камер, оснащенных продвинутым программным обеспечением, позволяет получать исходную экспериментальную информацию, которая для метода электронной спекл-интерферометрии имеет вид непрерывных карт фазовых распределений, в более простой форме, с большей скоростью и в большем объеме. Такой подход известен как метод корреляции цифровых изображений (Digital Image Correlation - DIC), который позволяет использовать для освещения поверхности исследуемого объекта источники полихроматического белого света (Gonzalez RC, Woods RE, Eddins SL. Digital Image Processing Using MATLAB. 1st ed. Pearson Education Inc.; 2004). Данный факт существенно упрощает оптическую схему экспериментального оборудования. Сущность метода DIC заключается в математической корреляции изменения распределения интенсивности волны, отраженной поверхностью до и после деформации объекта. Возможность регулировки чувствительности к тангенциальным компонентам перемещений, быстрое считывание и обработка данных измерений в большом количестве точек (N>1000) являются главными преимуществами метода корреляции цифровых изображений по сравнению с методом электронной спекл-интерферометрии. Определение величин КИН проводят тем же способом, который описан ранее для метода электронной спекл-интерферометрии, но на более простом и эффективном уровне с точки зрения получения и обработки экспериментальных данных (McNeill S.R., Peters W.H., Sutton М.А. Estimation of stress intensity factor by digital image correlation. Engineering Fracture Mechanics. - 1987. V. 28, №1. - P. 101-112; Roux S., Hild F. Stress intensity factor measurements from digital image correlation: post-processing and integrated approaches // International Journal of Fracture. - 2006. V. 140. - P. 141-157; Yoneyama S., Morimoto Y., Takashi M. Automatic evaluation of mixed-mode stress intensity factors utilizing digital image correlation // Strain. - 2006. V. 42, №1. - P. 21-29; Hamam R., Hild F., Roux S. Stress Intensity Factor Gauging by Digital Image Correlation: Application in Cyclic Fatigue // Strain. - 2007. V. 43, №3. - 181-192; Lopez-Crespo P., Shterenlikht A., Patterson E.A., Yates J.R., Withers P.J. The stress intensity of mixed mode cracks determined by digital image correlation // Journal of Strain Analysis. - 2008. V. 43, №8. - P. 769-780;  J., Roux S., Hild F. Noise-robust stress intensity factor determination from kinematic field measurements // Engineering Fracture Mechanics. - 2008. V. 75, №13. - P. 3763-3781; Yates J.R., Zanganeh M., Tai Y.H. Quantifying crack tip displacement fields with DIC // Engineering Fracture Mechanics. - 2010. V. 77, №11. - P. 2063-2076; Roux S.,
J., Roux S., Hild F. Noise-robust stress intensity factor determination from kinematic field measurements // Engineering Fracture Mechanics. - 2008. V. 75, №13. - P. 3763-3781; Yates J.R., Zanganeh M., Tai Y.H. Quantifying crack tip displacement fields with DIC // Engineering Fracture Mechanics. - 2010. V. 77, №11. - P. 2063-2076; Roux S.,  J., Hild F. Digital image correlation and fracture: an advanced technique for estimating stress intensity factors of 2D and 3D cracks // Journal of Physics D: Applied Physics. - 2009. V. 42, 214004. - P. 21, doi: 10.1088/0022-3727/42/21/214004; Mathieu F., Hild F., Roux S. Image-based identification procedure of a crack propagation law // Engineering Fracture Mechanics. - 2013. V. 103. - P. 48-59; Yusof F., Lopez-Crespo P., Withers P.J. Effect of overload on crack closure in thick and thin specimens via digital image correlation // International Journal of Fatigue. - 2013. V. 56. - P. 17-24; Lopez-Crespo P., Moreno В., Lopez-Moreno A., Zapatero J. Characterisation of crack-tip fields in biaxial fatigue based on high-magnification image correlation and electro-spray technique // International Journal of Fatigue. - 2015. V. 71. - P. 17-25; Mokhtarishirazabad M., Lopez-Crespo P., Moreno В., Lopez-Moreno A., Zanganeh M. Evaluation of crack-tip fields from DIC data: a parametric study // International Journal of Fatigue. - 2016. V. 89. - P. 11-19).
J., Hild F. Digital image correlation and fracture: an advanced technique for estimating stress intensity factors of 2D and 3D cracks // Journal of Physics D: Applied Physics. - 2009. V. 42, 214004. - P. 21, doi: 10.1088/0022-3727/42/21/214004; Mathieu F., Hild F., Roux S. Image-based identification procedure of a crack propagation law // Engineering Fracture Mechanics. - 2013. V. 103. - P. 48-59; Yusof F., Lopez-Crespo P., Withers P.J. Effect of overload on crack closure in thick and thin specimens via digital image correlation // International Journal of Fatigue. - 2013. V. 56. - P. 17-24; Lopez-Crespo P., Moreno В., Lopez-Moreno A., Zapatero J. Characterisation of crack-tip fields in biaxial fatigue based on high-magnification image correlation and electro-spray technique // International Journal of Fatigue. - 2015. V. 71. - P. 17-25; Mokhtarishirazabad M., Lopez-Crespo P., Moreno В., Lopez-Moreno A., Zanganeh M. Evaluation of crack-tip fields from DIC data: a parametric study // International Journal of Fatigue. - 2016. V. 89. - P. 11-19).
Типичная процедура, необходимая для извлечения величин КИН из полей перемещений, которые измерены в ближней и дальней окрестности вершины трещины, включает следующие основные этапы. Во-первых, исходные экспериментальные данные в терминах тангенциальных компонент перемещений u и ν, должны быть получены для значительного количества точек измерения до, и после приложения внешней нагрузки к образцу с трещиной фиксированной длины. Это количество может достигать несколько сотен для метода электронной спекл-интерферометрии и нескольких тысяч для метода корреляции цифровых изображений. Во-вторых, должна быть выбрана аналитическая функция, которая обладает способностью описания исследуемых полей напряжений и/или перемещений в окрестности вершины трещины. Значения этой функции во всех точках измерений должны быть поставлены в соответствие с полученными экспериментальными данными, чтобы определить искомые величины КИН. Большинство подходов, обеспечивающих достижение этой цели, основано на различных версиях метода наименьших квадратов. Для теоретического описания полей напряжений и перемещений в окрестности вершины трещины наиболее часто используют обобщенное разложение Вестергарда (Westergaard Н.М. Bearing pressures and cracks // Journal of Applied Mechanics. - 1939. V. 61. - P. A49-A59) или асимптотические ряды Уильямса (Williams M.L. On the stress distribution at the base of a stationary crack // ASME Journal of Applied Mechanics. - 1957. V. 24, №1. - P. 109-114). Представлен сравнительный анализ традиционных и новых математических моделей, используемых для извлечения величин КИН из больших массивов экспериментальных данных (Vasco-Olmo J.М., James М.N., Christopher С.J., Patterson Е.A.,  F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding // Fatigue & Fracture of Engineering Materials & Structures. - 2016. V. 39, №8. - P. 969-981).
F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding // Fatigue & Fracture of Engineering Materials & Structures. - 2016. V. 39, №8. - P. 969-981).
Представленная выше процедура может быть использована только для определения величин КИН в поле внешних напряжений. Кроме того, она имеет ряд очевидных недостатков. Первый из них заключается в необходимости использования значительного массива точек измерения. В настоящее время это не влияет на усложнение экспериментальных исследований. Наличие цифровых камер высокого разрешения, также как надежных алгоритмов и программного обеспечения для быстрой регистрации и обработки данных, практически уничтожает все технические проблемы, связанные с получением исходной экспериментальной информации с приемлемой точностью для большого количества точек. Основная проблема заключается в том, что точки измерения, расположенные на разных позициях по отношению к вершине трещины, дают исходные данные различной информационной ценности. Согласно принципам линейной механики разрушения, эта ценность увеличивается с уменьшением расстояния от каждой отдельной точки до вершины трещины (Сиратори М., Миёси Т., Мацусита X. Вычислительная механика разрушения. - М.: Мир, 1986. - 334 с.). Различие в информационной ценности между данными, полученными в различных точках массива измерений, может отрицательно сказываться на точности определения величин КИН. Действительно, точки, расположенные в дальнем поле содержат информацию, которая, в основном, относится к однородным полям напряжений и перемещений. Такая информация не имеет высокого качества с точки зрения определения величин параметров механики разрушения. С другой стороны, количество точек, находящихся на приемлемом расстоянии от вершины трещины, где может быть извлечена исходная информация высокого качества, всегда ограничено. Более того, область наибольшего интереса и информационной ценности, которая находится в непосредственной близости к вершине трещины, практически закрыта для измерений. Это обусловлено низкой корреляцией световых волн, диффузно рассеянных поверхностью объекта в исходном и деформированном состоянии, вследствие высоких градиентов деформаций и напряжений.
Таким образом, традиционная процедура определения КИН, основанная на измерении полей перемещений в окрестности трещины фиксированной длины при увеличении внешней нагрузки между двумя экспозициями, всегда требует преодоления ряда внутренних противоречий. Проблемы, проистекающие из этих противоречий, связаны с минимизацией погрешностей из-за наличия значительных по величине перемещений исследуемого объекта, как целого, и выбора оптимальной степени переопределенности исходных данных (Barker D.B., Sanford R.J., Chona R. Determining K and related stress-field parameters from displacement fields // Experimental Mechanics. - 1985. V. 25, №4. - P. 399-407). Серьезным фактором, который значительно усложняет минимизацию погрешностей экспериментальных данных, является необходимость предварительного определения точных координат вершины трещины (Zanganeh М., Lopez-Crespo P., Tai Y.H., Yates J.R. Locating the crack tip using displacement field data: a comparative study // Strain. - 2013. V. 49, №2. - P. 102-115). Кроме того, необходимо учитывать возможное различие между реальным напряженно-деформированным состоянием исследуемого объекта и аналитической моделью, используемой для обработки данных измерений.
Существует единственный подход к экспериментальному определению величин КИН, который можно использовать для трещин в поле, как внешних, так и остаточных напряжений. Этот подход, основанный на последовательном увеличении длины узкого разреза, моделирующего продвижение трещины, был первоначально предложен для определения остаточных напряжений Vaidyanathan, Finnie и Cheng и известен как метод последовательного наращивания длины трещины - ПНДТ (the crack compliance method - CCM) (Vaidyanathan S, Finnie I. Determination of residual stresses from stress intensity factor measurement // Journal of Basic Engineering. - 1971. V. 93. - P. 242-246; Cheng W., Finnie I. Measurement of residual hoop stresses in cylinders using the compliance method // ASME Journal of Engineering Materials and Technology. - 1986. V. 108, №2. - P. 87-92). В отличие от описанного выше подхода, метод ПНДТ использует измерение деформационного отклика на малое приращение длины трещины без изменения условий внешнего нагружения. Идея этого метода основана на релаксации исходного поля напряжений вследствие введения узкого разреза прогрессивно увеличивающейся длины и измерении соответствующего изменения деформированного состояния с помощью тензометрического датчика (Prime М.В. Measuring residual stress and the resulting stress intensity factor in compact tension specimen // Fatigue & Fracture of Engineering Materials & Structures. - 1992. V. 22, №3. - P. 195-204).
Исходная версия метода ПНДТ требует использования сложных математических моделей и направлена на определение остаточных напряжений. В качестве следующего шага Schindler разработал более простую версию, основанную на соотношениях линейной механики разрушения (Schindler H.-J. Determination of residual stress distributions from measured stress intensity factors // International Journal of Fracture. - 1995. V. 74, №2. - P. R23-R30). Только такой подход дает величины КИН для трещин в поле внешних, остаточных и комбинированных напряжений как функцию длины разреза без предварительного определения остаточных напряжений.
Наиболее близким техническим решением, выбранным в качестве прототипа предлагаемого способа, является способ определения КИН для трещины в поле остаточных напряжений в металлическом диске, заключающийся в том, что в выбранной точке образца устанавливают тензометрический датчик, моделируют трещину последовательностью узких надрезов в радиальном направлении, измеряют деформацию (деформационный отклик), вызванную увеличением длины трещины, выбирают математическую модель, которая связывает измеренные деформации с величинами КИН, определяют функцию влияния и с ее помощью вычисляют величины КИН для трещин различной длины в исследуемом образце (Schindler H.-J., Cheng W., Finnie I. Experimental determination of stress intensity factors due to residual stresses // Experimental Mechanics. - 1997. V. 37, №3. - P. 272-277).
В настоящее время традиционная верстия метода ПНДТ достаточно широко используется для оценки скорости роста трещины в окрестности продвинутых сварных соединений авиационных конструкций (Sutton М.А., Reynolds А.Р., Ge Y.Z., Deng X. Limited weld residual stress measurements in fatigue crack propagation: Part II. FEM-based fatigue crack propagation with complete residual stress fields // Fatigue & Fracture of Engineering Materials & Structures - 2006. V. 29. N7. - P. 537-545; Ghidini Т., Dalle Donne C. Fatigue crack propagation assessment based on residual stresses obtained through cut-compliance technique // Fatigue & Fracture of Engineering Materials & Structures - 2007. V. 30. N 3. - P. 214-222; Milan M.T., Bose Filho W.W., Ruckert C.O.F.T., Tarpani J.R. Fatigue behaviour of friction stir welded AA2024-T3 alloy: longitudinal and transverse crack growth // Fatigue & Fracture of Engineering Materials & Structures - 2008. V. 31. N 7. - P. 526-538; Pasta S., Reynolds A.P. Evaluation of Residual Stresses During Fatigue Test in an FSW Joint // Strain - 2008. V. 44. N 2. - P. 147-152; Pouget G., Reynolds A.P. Residual stress and microstructure effects on fatigue crack growth in AA2050 friction stir welds alloys // International Journal of Fatigue. - 2008. V. 30, N 3. - P. 463-472; Fratini L., Pasta S., Reynolds A.P. Fatigue crack growth in 2024-T351 friction stir welded joints: Longitudinal residual stress and microstructural effects // International Journal of Fatigue. - 2009. V. 31, N 3. - P. 495-500). Следует, однако, отметить, что исходная экспериментальная схема сохраняется в неизменном виде. Конкретно говоря, требуемые измерения выполняются, в лучшем случае, с помощью набора тензодатчиков, которые расположены на значительном расстоянии от вершины трещины. Такой путь экспериментальной реализации метода ПНДТ не свободен от ряда недостатков. Во-первых, значительное расстояние между точкой измерения и вершиной трещины снижает чувствительность метода по отношению к определяемым параметрам механики разрушения. Главный недостаток традиционного подхода заключается в необходимости создания сложной численной модели, которая необходима для корректной интерпретации исходной экспериментальной информации в терминах КИН. Такая модель должна быть создана для каждого конкретного объекта исследования. Точечный характер измерений не дает возможности надежно установить реальный тип исследуемого напряженного состояния, что необходимо для верификации используемой численной модели. Все эти факторы отрицательным образом влияют на надежность и точность конечного результата.
Техническим результатом данного изобретения является повышение точности измерения КИН для трещин при воздействии внешних и, особенно, остаточных напряжений, необходимое для повышения ресурса и надежности тонкостенных элементов авиационных конструкций при их эксплуатации за счет учета эволюции параметров механики разрушения вследствие циклического нагружения. Ключевым моментом разработанного подхода является возможность измерения деформационного отклика, вызванного локальным удалением материала между двумя экспозициями, методом электонной спекл-интерферометрии в ограниченном числе точек, которые расположены непосредственно на берегах трещины.
Технический результат достигается тем, что в способе определения коэффициентов интенсивности напряжений для трещин, включающим установку образца, увеличение длины трещины на малое приращение с помощью разреза и измерение деформационного отклика, образец устанавливают в оптическую схему интерферометра, регистрируют исходное состояние спекл-структуры поверхности видеокамерой, после увеличения длины трещин регистрируют спекл-структуру деформированного состояния поверхности образца, визуализируют картину интерференционных полос на основе полученных изображений, определяют раскрытие трещины в точке начала приращения ее длины и в центральной точке этого приращения и определяют величину коэффициента интенсивности напряжений для трещины длиной аn расчетным методом.
В качестве расчетного метода используют формулу:
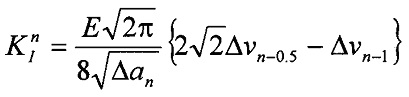 ,
,
где Е - модуль упругости материала; Δаn - приращение длины трещины; Δνn-1 - величина раскрытия трещины в точке начала приращения ее длины n-1; Δνn-0.5 - величина раскрытия трещины в центральной точке приращения ее длины n-0.5.
Техническое решение поясняется следующими чертежами.
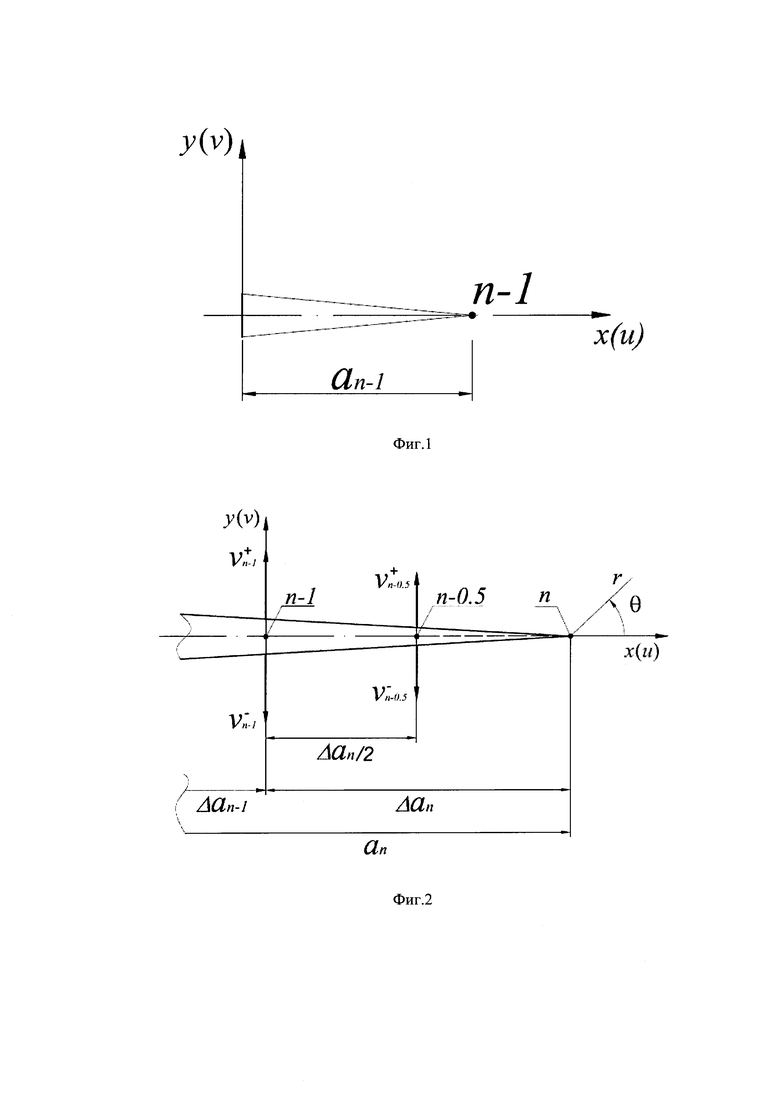
Фиг. 1 - представлена схема исходной трещины длиной an-1.
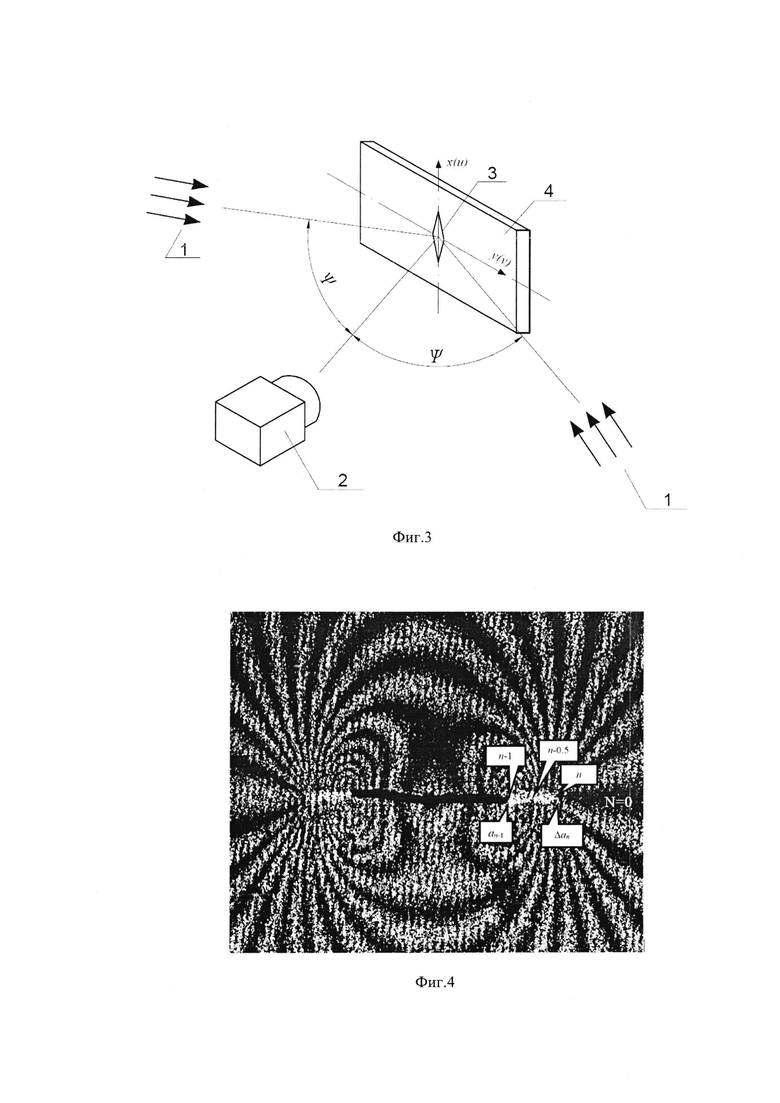
Фиг. 2 - представлена схема конечной трещины длиной an и полярная система координат с началом в вершине трещины и обозначения, принятые для определения коэффициента интенсивности напряжений (КИН); n-1 и n - начальная и конечная точки приращения длины трещины.
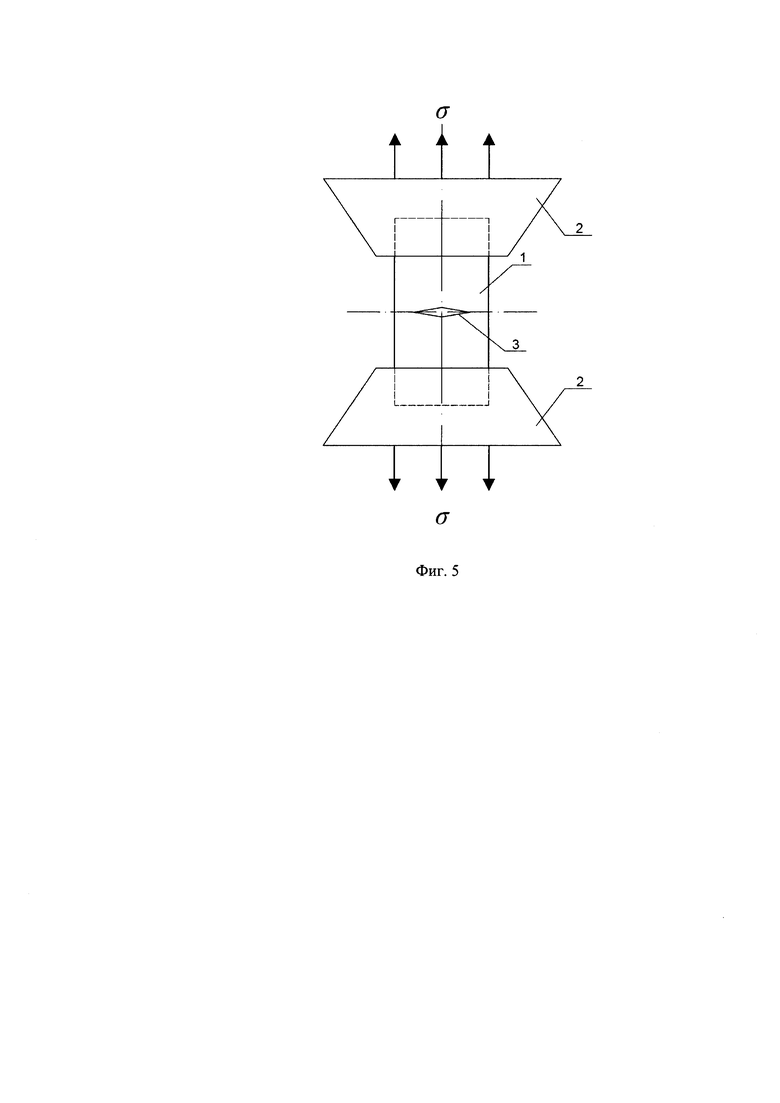
Фиг. 3 - представлена общая схема спекл-интерферометра для определения тангенциальной компоненты перемещения ν, характеризующей раскрытие трещины.
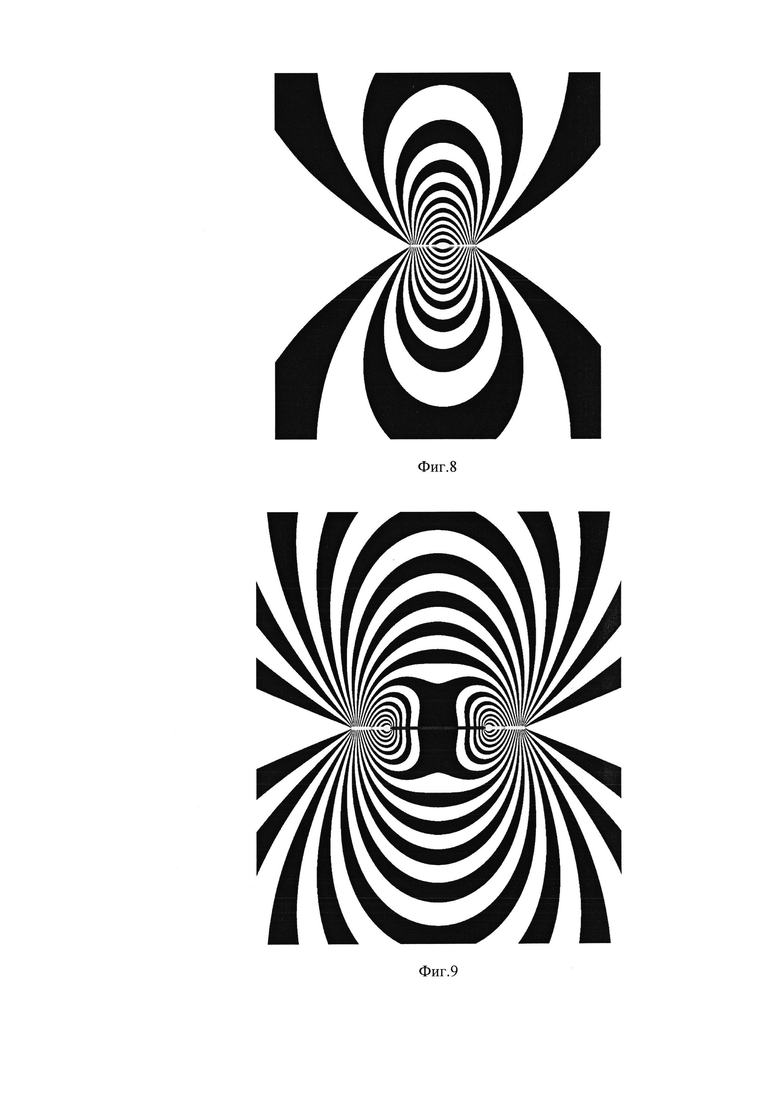
Фиг.4 - представлена интерферограмма, полученная в терминах тангенциальной компоненты перемещений ν при одноосном растяжении прямоугольной пластины с центральной симметричной трещиной и схема расположения точек измерения n-1 и n-0.5 на реальной картине интерференционных полос.
Фиг. 5 - представлена схема одноосного нагружения прямоугольной пластины с центральной симметричной трещиной растягивающими напряжениями σ.
Фиг. 6 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты ν при одноосном растяжении пластины с центральной симметричной трещиной длиной 2a1=5.04 мм.
Фиг. 7 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты ν при одноосном растяжении пластины с центральной симметричной трещиной длиной 2а2=9.18 мм.
Фиг. 8 - представлена картина образцовых интерференционных полос, полученная в терминах тангенциальной компоненты ν путем моделирования одноосного растяжения пластины с центральной симметричной трещиной длиной 2a1=5.04 мм.
Фиг. 9 - представлена картина образцовых интерференционных полос, полученная в терминах тангенциальной компоненты ν путем моделирования одноосного растяжения пластины с центральной симметричной трещиной длиной 2а2=9.18 мм.
Фиг. 10 - представлен чертеж образца в форме трапецеидальной двухконсольной балки (ТДКБ) и схема его нагружения.
Фиг. 11 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты ν при внецентренном растяжении ТДКБ образца для трещины длинной а3=26.35 мм.
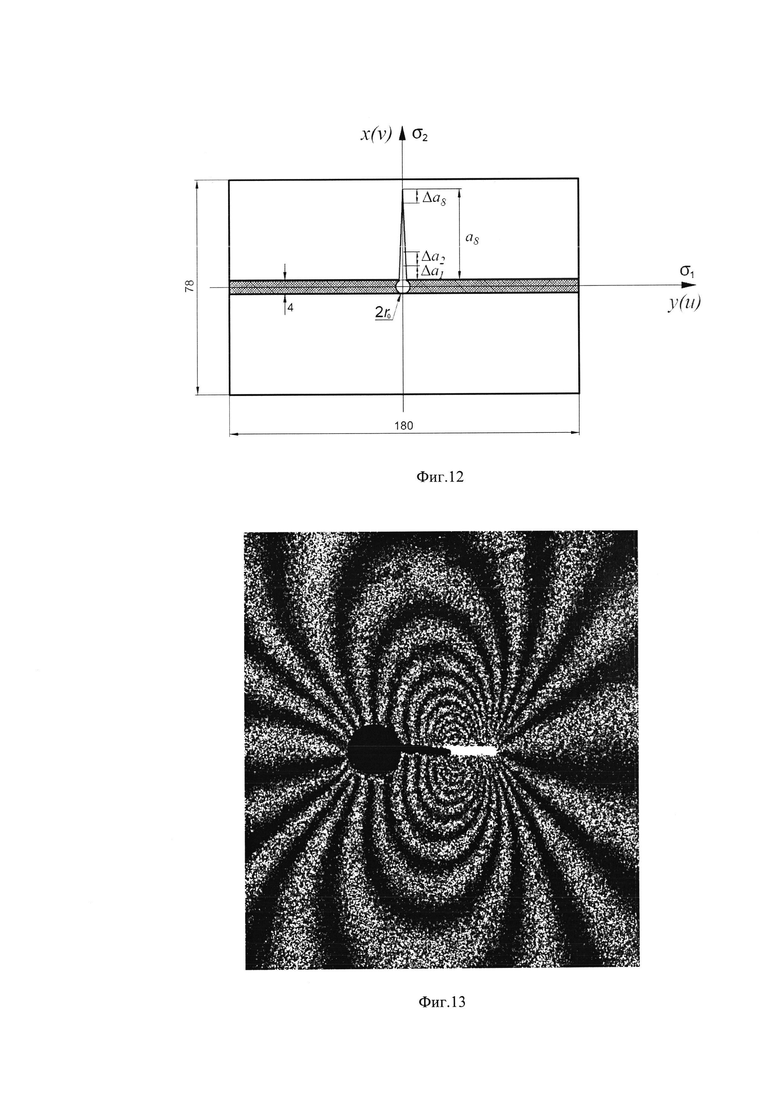
Фиг. 12 - представлен чертеж прямоугольного образца со сварным швом, используемая система координат и схема моделирования трещины последовательностью узких разрезов.
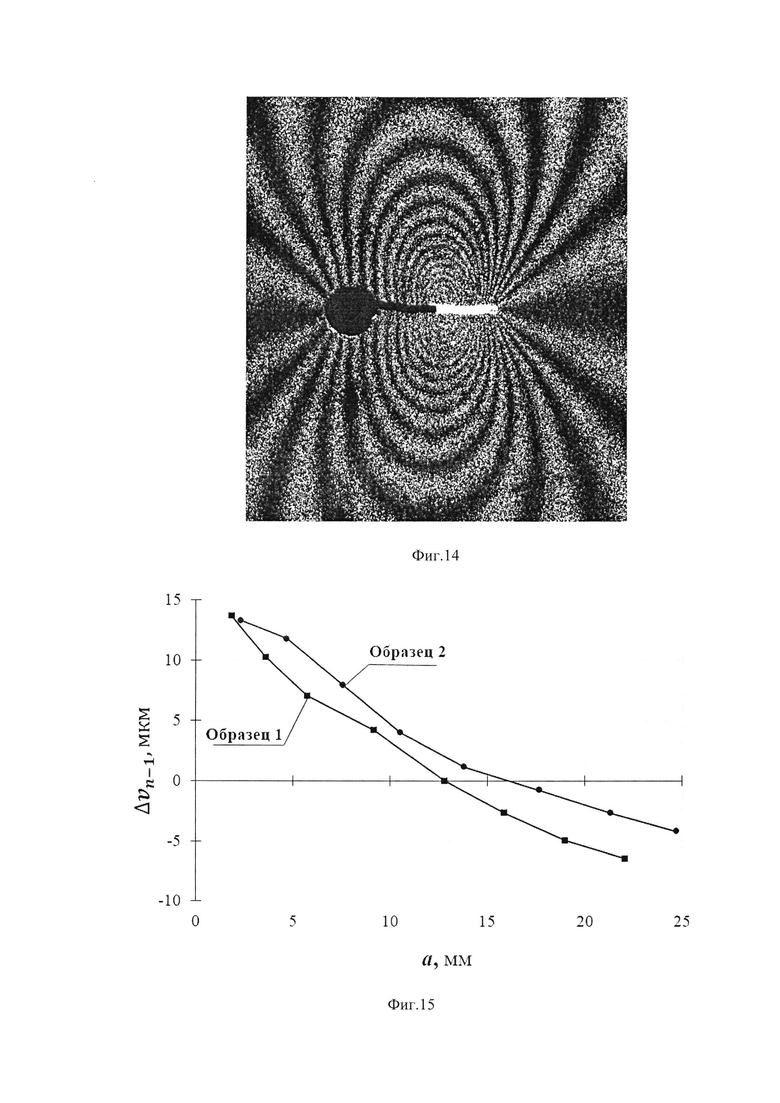
Фиг. 13 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты ν для трещины длиной а2=3.88 мм в исходном поле остаточных напряжений.
Фиг. 14 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты ν для трещины длиной а2=4.68 мм в поле остаточных напряжений после циклического нагружения.
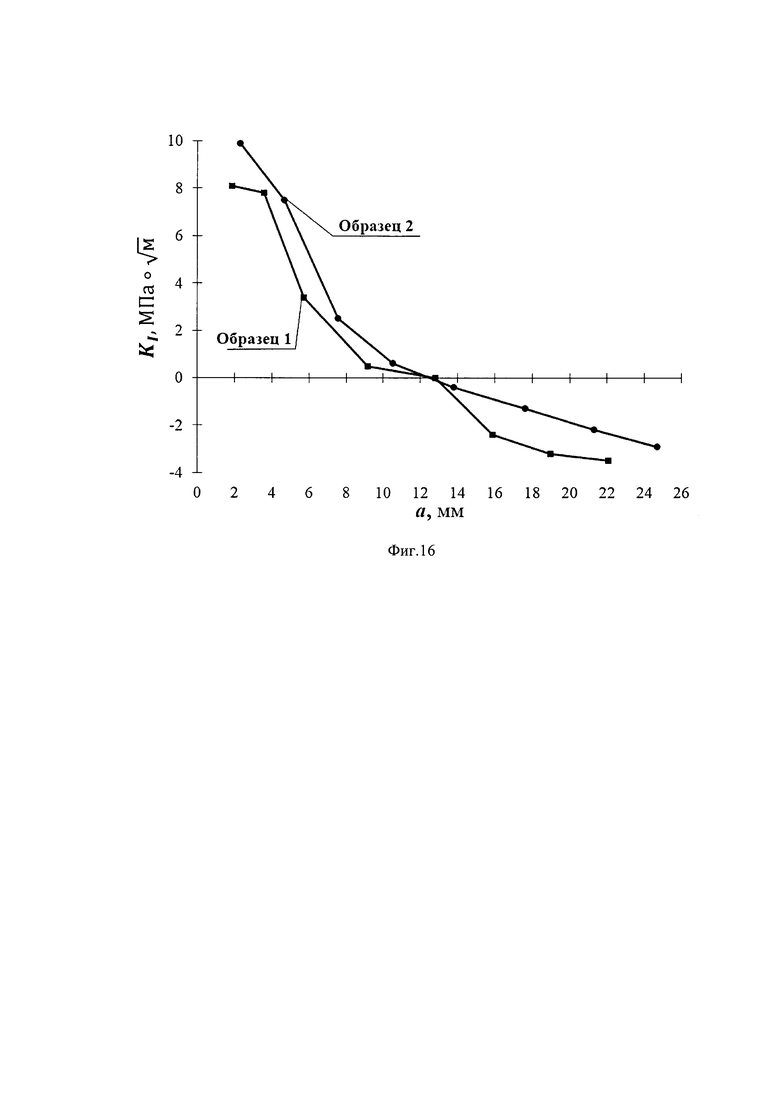
Фиг. 15 - представлены зависимости величин раскрытия трещины, измеренные в точке начала приращения ее длины, от длины трещины для образца в исходном состоянии и в образце после циклического нагружения.
Фиг. 16 - представлены зависимости величин КИН от длины трещины для образца в исходном состоянии и в образце после циклического нагружения.
Коэффициент интенсивности напряжений определяется на основе модифицированной версии метода последовательного наращивания длины трещины (ПНДТ). Сущность модифицированной версии метода ПНДТ заключается в регистрации картин интерференционных полос, которые соответствуют разнице между двумя полями плоских компонент перемещений. Каждое поле относится к трещине близкой, но различной длины. Первая экспозиция выполняется для исходной трещины длиной an-1 (фиг. 1). Затем исходная трещина увеличивается на величину малого приращения Δan так, что суммарная длина трещины становится равной аn=an-1+Δan и осуществляется второе экспонирование поверхности исследуемого объекта (фиг. 2). Картины интерференционных полос визуализируются численным вычитанием двух изображений, зарегистрированных для двух трещин различной длины.
Для этого используется оптическая схема с двумя симметричными направлениями освещения 1 и нормальным по отношению к плоской поверхности объекта направлением наблюдения, вдоль которого расположена высокоразрешающая видео камера 2 (фиг. 3). Два изображения исследуемого участка поверхности, соответствующие исходной и конечной длинам трещин 3 в пластине 4, последовательно регистрируют высокоразрешающей видео камерой и сохраняют в виде цифровых файлов. Визуализацию картин интерференционных полос осуществляют путем цифрового вычитания соответствующих изображений. Типичная интерферограмма, которая получена таким способом для тонкой прямоугольной пластины размерами 180×30×4 мм со сквозной симметричной трещиной типа I, показана на фиг. 4. Эта интерферограмма соответствует одноосному растяжению образца номинальными напряжениями σ=60 МПа (фиг. 5).
Разработанная процедура извлечения величин КИН по данным количественных измерений порядков интерференционных полос в точках, расположенных на берегах трещины, основана на формулировке Уильямса (Williams M.L. On the stress distribution at the base of a stationary crack // ASME Journal of Applied Mechanics. - 1957. V. 24, №1. - P. 109-114). В соответствии с этим подходом тангенциальная компонента перемещений ν, необходимая для определения КИН, в окрестности вершины трещины выражается в виде бесконечного ряда. Когда направление оси x совпадает с линией трещины, выражение для трещины типа I (трещины нормального отрыва) принимает следующий вид:
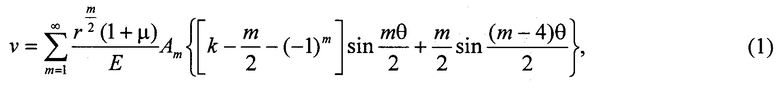
где ν - тангенциальная компонента перемещений в направлении оси y; Е - модуль упругости материала; μ - коэффициент Пуассона; k=(3-μ)/(1+μ) для условий плоской деформации; k=(3-4μ) для плоского напряженного состояния; Аm - постоянные коэффициенты, подлежащие определению; r и θ - радиальное и угловое расстояние от вершины трещины (фиг. 2). Величина коэффициента интенсивности напряжений (КИН) K1 связана с коэффициентами ряда (1) следующим образом (Yates J.R., Zanganeh M, Tai Y.H. Quantifying crack tip displacement fields with DIC // Engineering Fracture Mechanics. - 2010. V. 77. №11. - P. 2063-2076):

В предлагаемом способе величина коэффициента А1 определяется из решения линейной алгебраической системы уравнений, формируемой на основе ряда (1) с использованием первых двух нечетных коэффициентов. Правая часть этой системы уравнений составляется на основе экспериментальных данных. Эти данные представляют собой тангенциальные компоненты перемещений ν, которые измеряются непосредственно на берегах разреза, моделирующего трещину.
В общем случае исходная экспериментальная информация представляет собой разницу абсолютных величин плоских компонент перемещений Vn для двух трещин длиной аn и аn-1:
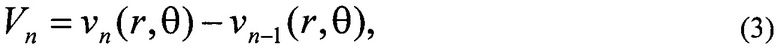
где (r, θ) - полярные координаты рассматриваемых точек для системы координат, начало которой расположено в точке n (фиг. 2); νn-1(r, θ) - абсолютные значения тангенциальной компоненты перемещений в точке с координатами (r, θ) для трещины длиной аn-1; νn(r, θ) - абсолютные значения тангенциальной компоненты перемещений ν в точке с координатами (r, θ) для трещины длиной аn.
Соотношение (3) справедливо для любой точки в окрестности вершины трещины. Однако в правой части уравнений (3) содержатся относительные величины компонент перемещений, которые не могут быть использованы для непосредственного определения требуемых величин Аm из разложения (1). Главная особенность разработанного подхода заключается в том, что каждая интерференционная картина типа, показанного на фиг. 3, содержит несколько особых точек, расположенных непосредственно на границе трещины. Абсолютные величины плоских компонент перемещений ν и затем величины коэффициентов Аm из формул (1) для трещины длинной аn могут быть определенны в этих точках.
При определении величины КИН используются особые точки, расположенные вдоль линии трещины между точками n-1 и n, где компоненты перемещений νn-1 равны нулю перед увеличением длины трещины. Соотношение (3) справедливо для любой точки, принадлежащей окрестности вершины трещины. Однако правая часть уравнения (3) содержит относительные величины компоненты перемещений ν, которые не могут напрямую использоваться для определения коэффициентов Аm из разложения (1). Главная особенность предлагаемого подхода заключается в том, что каждая картина интерференционных полос типа, показанного на фиг. 3, включает набор особых точек, расположенных непосредственно на берегах трещины. Перемещения в этих точках удовлетворяют условию:

Соотношение (4) свидетельствует, что абсолютные величины тангенциальных компонент перемещений ν в особых точках могут быть определены для трещины длиной аn следующим образом:

где νn-1{r, θ) определяются с помощью любой интерферограммы типа, показанного на фиг. 4. Абсолютные величины тангенциальной компоненты νn(r, θ) позволяют получить коэффициенты Аm рядов (1) и, следовательно, величины КИН.
Таким образом, каждая картина полос типа, показанного на фиг. 4, обеспечивает определение абсолютных величин тангенциальной компоненты ν для каждой точки с полярными координатами 0≤r≤аn, θ=π (фиг. 2). Распределение компоненты перемещений ν, которая соответствует первому и третьему членам бесконечного ряда (1) для полярной системы координат с началом в вершине трещины длиной аn (фиг. 2), выражается как:
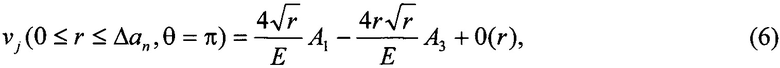
где j определяет номер точки в указанном интервале для трещины длиной аn. Соотношение (6) показывает, что определение величины KI из формулы (2) требует измерения величин компоненты ν как минимум в двух точках интервала 0≤r≤Δаn, θ=π. С измерительной точки зрения первое уравнение наиболее удобно получить для начальной точки приращения длины трещины j=n-1. Эта точка легко идентифицируется на картине полос как начальная точка яркого участка разреза (фиг. 4). При этом определяется величина раскрытия берегов трещины, которая равна удвоенному абсолютному значению компоненты перемещений νn-1. Подстановка обозначений r=Δаn и 2νj(r=Δаn, θ=π)=2νn-1=Δνn-1 в соотношение (6), без учета членов разложения (1) со степенями m≥5, сумма которых обозначена как 0(r) дает:
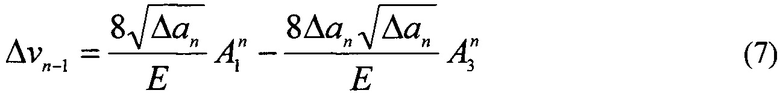
где 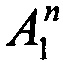 и
и  - коэффициенты разложения (1) для трещины длинной аn. Второе необходимое уравнение целесообразно составить для точки с координатами r=Δаn/2, чтобы обеспечить максимально возможное пространственное разрешение между двумя точками измерений на линии приращения длины трещины (фиг. 2, фиг. 4). Выбор данной точки связан с тем фактом, что для точек с координатами r=Δаn/2 определение порядков интерференционных полос на линии трещины может представлять значительные экспериментальные проблемы. Подстановка величины r=Δаn/2 и 2νj(r=Δаn/2, θ=π)=2νn-0.5=Δνn-0.5 соотношение (6) дает:
- коэффициенты разложения (1) для трещины длинной аn. Второе необходимое уравнение целесообразно составить для точки с координатами r=Δаn/2, чтобы обеспечить максимально возможное пространственное разрешение между двумя точками измерений на линии приращения длины трещины (фиг. 2, фиг. 4). Выбор данной точки связан с тем фактом, что для точек с координатами r=Δаn/2 определение порядков интерференционных полос на линии трещины может представлять значительные экспериментальные проблемы. Подстановка величины r=Δаn/2 и 2νj(r=Δаn/2, θ=π)=2νn-0.5=Δνn-0.5 соотношение (6) дает:
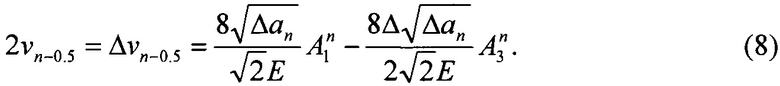
Коэффициенты 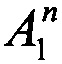 и
и 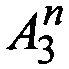 определяются из решения системы линейных алгебраических уравнений (7) и (8):
определяются из решения системы линейных алгебраических уравнений (7) и (8):
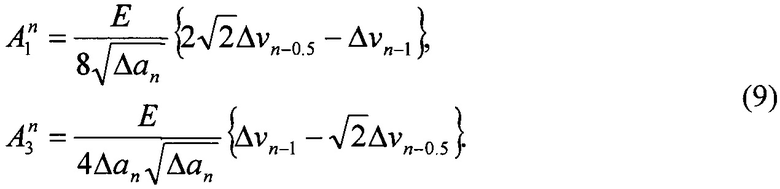
Величина КИН KI следует из подстановки полученного результата (9) в уравнение (2):

Для экспериментального определения величин КИН KI используются картины интерференционных полос типа, представленного на фиг. 4. На этом рисунке показаны позиции точек n, n-0.5 и n-1, которые соответствуют обозначениям на фиг. 2. Величины раскрытия трещины в двух точках Δνn-1 и Δνn-0.5, которые необходимы для определения величины КИН согласно формуле (10), определяют методом электронной спекл-интерферометрии, применяя оптическую схему, показанную на фиг. 3.
Когда проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси у (фиг. 3), то картина интерференционных полос, соответствующая тангенциальной компоненте перемещений ν в направлении раскрытия трещины, описывается следующим образом:

где Nν=±1; ±2; ±3, … - абсолютные порядки интерференционных полос; λ - длина волны лазерного освещения; Ψ=π/4 - угол между наклонным направлением освещения и нормальным к поверхности плоского объекта направлением наблюдения. Идентификацию физического знака компонент перемещений проводят методом регистрации интерферограмм с дополнительным фазовым сдвигом, направление которого задают известным образом (Pisarev VS, Odintsev IN, Apalkov AA, Chernov AV. Role of high-quality interference fringe patterns for the residual stress determination by the hole-drilling method / Visualization of Mechanical Processes 2011; Vol. 1. N 1. DOI: 10.1615/VisMechProc.v 1.i1.40).
Измерения раскрытия трещины проводятся в двух точках n-1 и n-0.5 с координатами (r=Δan, θ=π) и (r=Δan/2, θ=π), соответственно, как это показано на фиг. 2 и фиг. 4. Точка n-1 легко идентифицируется на любых интерференционных картинах типа, показанного на фиг. 4, как граница между темным и ярким участками линии разреза. Точка n-0.5 расположена в центре яркого участка линии разреза, который соответствует приращению длины трещины Δan. Величина раскрытия трещины в точке n-1, обозначенная как 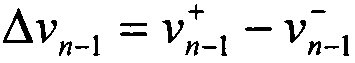 , определяется следующим образом. Во-первых, нужно определить абсолютные порядки полос на верхнем и нижнем берегах трещины, которые соответствуют компонентам перемещений
, определяется следующим образом. Во-первых, нужно определить абсолютные порядки полос на верхнем и нижнем берегах трещины, которые соответствуют компонентам перемещений  и
и 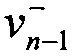 , соответственно. Это осуществляется прямым подсчетом от нулевой полосы N=0, позиция которой указана на фиг. 4. После этого компоненты перемещений вычисляются согласно соотношениям (11):
, соответственно. Это осуществляется прямым подсчетом от нулевой полосы N=0, позиция которой указана на фиг. 4. После этого компоненты перемещений вычисляются согласно соотношениям (11):
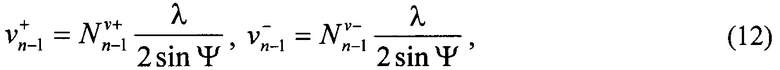
где  и
и 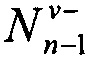 - абсолютные порядки полос на верхнем и нижнем берегах трещины, соответственно; λ - длина волны лазерного излучения; Ψ=π/4 - угол чувствительности. При этом следует учитывать, что
- абсолютные порядки полос на верхнем и нижнем берегах трещины, соответственно; λ - длина волны лазерного излучения; Ψ=π/4 - угол чувствительности. При этом следует учитывать, что  и
и 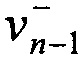 , также как
, также как 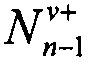 и
и 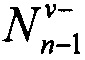 имеют противоположные физические знаки. Раскрытие трещины Δνn-1 в точке начала ее приращения n-1 (CMOD) определяется из соотношения (12) следующим образом:
имеют противоположные физические знаки. Раскрытие трещины Δνn-1 в точке начала ее приращения n-1 (CMOD) определяется из соотношения (12) следующим образом:
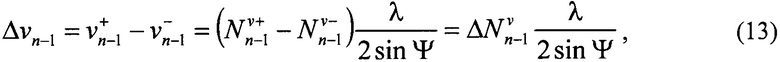
где 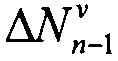 - разница абсолютных порядков полос в точке n-1. Эта величина подсчитывается по одной интерферограмме типа, показанного на фиг. 4, между двумя точками, которые расположены на противоположных берегах разреза. Для этого используются интерференционные изображения большого масштаба. Величина раскрытия трещины в точке n-0.5 (фиг. 2), обозначенная как
- разница абсолютных порядков полос в точке n-1. Эта величина подсчитывается по одной интерферограмме типа, показанного на фиг. 4, между двумя точками, которые расположены на противоположных берегах разреза. Для этого используются интерференционные изображения большого масштаба. Величина раскрытия трещины в точке n-0.5 (фиг. 2), обозначенная как 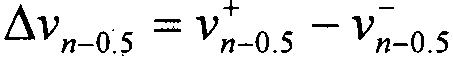 , определяется тем же способом. Таким образом, два экспериментально измеренных параметра, а именно CMOD Δνn-1 (13) и COD Δνn-0.5, имеются в наличии и могут быть использованы для определения величин КИН по формуле (10).
, определяется тем же способом. Таким образом, два экспериментально измеренных параметра, а именно CMOD Δνn-1 (13) и COD Δνn-0.5, имеются в наличии и могут быть использованы для определения величин КИН по формуле (10).
Реализация предлагаемого способа осуществляется следующим образом.
Исследуемый образец в виде прямоугольной пластины, изготовленной из металлического материала 1, устанавливают в захватах испытательной машины 2 и нагружают растягивающими напряжениями σ (фиг. 5) при исследовании трещин 3 в поле внешних или комбинированных напряжений. При исследовании трещин в поле остаточных напряжений внешнее нагружение не требуется. Образец устанавливают в оптическую схему интерферометра, освещают его поверхность двумя плоскими волнами 1 (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси y, и регистрируют с помощью высокоразрешающей цифровой видеокамеры 2 спекл-структуру поверхности пластины в исходном состоянии для длины трещины an-1 (фиг. 1), необходимую для определения компоненты перемещений ν (цифровой файл V1). Увеличивают длину трещины 3 на малое приращение на величину Δan. Освещают поверхность образца 4 двумя плоскими волнами (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси у, и регистрируют спекл-структуру поверхности пластины для трещины длиной an, необходимую для определения компоненты перемещений ν (цифровой файл V2). Проводят численное вычитание файлов V2-V1 и тем самым визуализируют картину интерференционных полос, по которой определяют величины раскрытия трещины в начальной точке приращения ее длины Δνn-1 и в центральной точке этого приращения Δνn-0.5, необходимые для вычисления коэффициентов интенсивности напряжений согласно формуле (10).
1. Предлагаемым способом проводилось определение КИН для центральной симметричной трещины в образце размерами 180×30×4 мм, изготовленном из алюминиевого сплава (E=72000 МПа, μ=0.33). Исходная точка симметричной трещины, которая представляет собой малое отверстие диаметром 2R0=5 мм, расположена в центре пластины. Отсутствие остаточных напряжений в образце было установлено на основе совместного применения метода сверления отверстия и измерения приращений диаметров отверстия в направлении главных напряжений (Pisarev VS, Odintsev IN, Apalkov AA, Chernov AV. Role of high-quality interference fringe patterns for the residual stress determination by the hole-drilling method / Visualization of Mechanical Processes 2011; Vol. 1. N 1. DOI: 10.1615/VisMechProc.v1.i1.40). Трещина моделируется последовательностью узких разрезов шириной Δb=0.2 мм. Образец подвергался равномерному одноосному растяжению с помощью электромеханической испытательной машины waiter + bai ag, Type LFM-L 25 с диапазоном нагружения 0÷25 кН. Две интерферограммы, полученные для образца с центральной симметричной трещиной при действии растягивающей нагрузки P=7.20 кН в терминах компоненты перемещений ν, показаны на фиг. 6 (исходная длина трещины а0=0 с приращениями 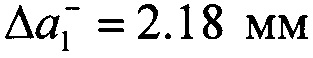 (левая) и
(левая) и 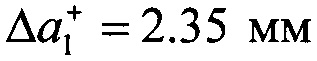 (правая)) и фиг. 7 (исходная длина трещины
(правая)) и фиг. 7 (исходная длина трещины 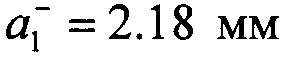 и
и 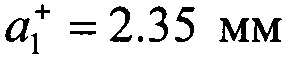 , с приращениями
, с приращениями  (левая) и
(левая) и 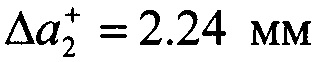 (правая)). Оба изображения имеют размер 25×25 мм. Справа на картинах полос отмечена нулевая полоса, необходимая для получения исходных экспериментальных данных. Слева на этих изображениях показан способ подсчета разницы абсолютных порядков полос
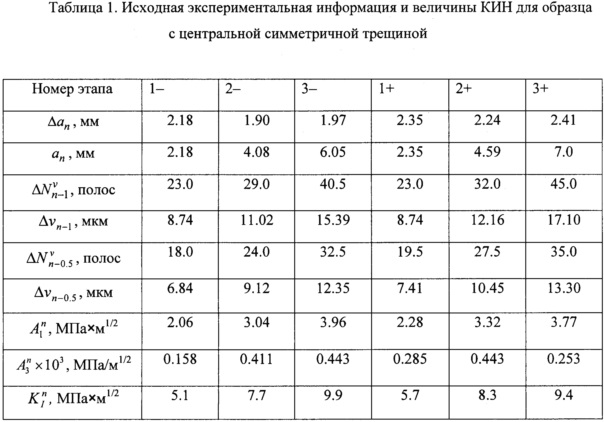
(правая)). Оба изображения имеют размер 25×25 мм. Справа на картинах полос отмечена нулевая полоса, необходимая для получения исходных экспериментальных данных. Слева на этих изображениях показан способ подсчета разницы абсолютных порядков полос  в точке n-1 для левой половины трещины. Необходимо отметить высокое качество представленных интерферограмм, которое обеспечивают надежное определение величин разницы абсолютных порядков полос. Наблюдается также практически полная симметрия картин интерференционных полос по отношению к линии трещины. Это означает, что трещина соответствует условию нормального отрыва. Таким образом, полученная экспериментальная информация может быть использована для подсчета величин КИН по формуле (10). Исходная экспериментальная информация необходимая для определения коэффициента А1 рядов (1) и дальнейшего вычисления величин КИН представлена в табл. 1.
в точке n-1 для левой половины трещины. Необходимо отметить высокое качество представленных интерферограмм, которое обеспечивают надежное определение величин разницы абсолютных порядков полос. Наблюдается также практически полная симметрия картин интерференционных полос по отношению к линии трещины. Это означает, что трещина соответствует условию нормального отрыва. Таким образом, полученная экспериментальная информация может быть использована для подсчета величин КИН по формуле (10). Исходная экспериментальная информация необходимая для определения коэффициента А1 рядов (1) и дальнейшего вычисления величин КИН представлена в табл. 1.
При проведении экспериментов используется простейшая схема интерферометра без привлечения каких-либо электронных или цифровых элементов. Поэтому, подсчет количества интерференционных полос проводится невооруженным глазом оператора. Данный подход означает, что величина погрешности равна δN=0.5 полосы, что составляет разницу между соседними светлой и темной полосами. Оценку влияния этой погрешности на результат определения КИН проводят следующим образом. Наиболее трудная ситуация возникает при подсчете величины ΔNn-0.5. Рассмотрим для примера определение этой величины для трещины длиной 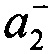 . Изменение величины ΔNn-0.5 с 24.0 до 24.5 полос дает
. Изменение величины ΔNn-0.5 с 24.0 до 24.5 полос дает  вместо
вместо 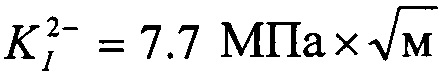 из табл. 1. Разница составляет 2.5%. Для дальнейшей оценки погрешности определения величин КИН используются усредненные величины длин трещин и КИН, как это показано в табл. 2. Такой подход необходим, так как обеспечение равной длинны правой и левой трещины в ходе эксперимента представляет достаточно трудную техническую задачу. Первая строка этой таблицы включает осредненные величины половины суммарной длины трещины. Теоретические величины из третьей строки табл. 2 соответствуют соотношению из раздела 5.1 справочника Мураками (Справочник по коэффициентам интенсивности напряжений: В 2-х томах. Т. 1: Пер. с англ. / Под ред. Ю. Мураками. - М.: Мир, 1990. - 448 с.):
из табл. 1. Разница составляет 2.5%. Для дальнейшей оценки погрешности определения величин КИН используются усредненные величины длин трещин и КИН, как это показано в табл. 2. Такой подход необходим, так как обеспечение равной длинны правой и левой трещины в ходе эксперимента представляет достаточно трудную техническую задачу. Первая строка этой таблицы включает осредненные величины половины суммарной длины трещины. Теоретические величины из третьей строки табл. 2 соответствуют соотношению из раздела 5.1 справочника Мураками (Справочник по коэффициентам интенсивности напряжений: В 2-х томах. Т. 1: Пер. с англ. / Под ред. Ю. Мураками. - М.: Мир, 1990. - 448 с.):

Во всех случаях из табл. 2 коэффициент F из соотношения (14) равен F=1. Четвертая строка табл. 2 содержит разницу между экспериментальными и теоретическими величинами 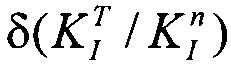 . Секция 1.1 справочника Мураками содержит теоретические величины КИН для центральной трещины в прямоугольной пластине ограниченной ширины при одноосном растяжении. Эти данные так же описываются соотношением (14). Величины коэффициентов F приведены в 5-й строке табл. 2. Последняя строка этой таблицы отражает разницу между экспериментальными и теоретическими величинами КИН в рассмотренном случае. Теоретические величины КИН из раздела 1.1 справочника Мураками находятся в полном соответствии с надежными результатами метода конечных элементов (Jogdand P.V., Murthy K.S.R.K. A finite element based interior collocation method for the computation of stress intensity factors and T-stresses // Engineering Fracture Mechanics. - 2010. V. 77. №7. - P. 1116-1127). Сравнение экспериментальных, теоретических и расчетных данных приведенных в табл. 2, наглядно демонстрирует, что использование двух первых нечетных коэффициентов рядов (1), полученных по результатам измерений раскрытия в двух точках на берегах трещины, обеспечивает точность определения величин КИН, которая достаточна для большинства инженерных приложений.
. Секция 1.1 справочника Мураками содержит теоретические величины КИН для центральной трещины в прямоугольной пластине ограниченной ширины при одноосном растяжении. Эти данные так же описываются соотношением (14). Величины коэффициентов F приведены в 5-й строке табл. 2. Последняя строка этой таблицы отражает разницу между экспериментальными и теоретическими величинами КИН в рассмотренном случае. Теоретические величины КИН из раздела 1.1 справочника Мураками находятся в полном соответствии с надежными результатами метода конечных элементов (Jogdand P.V., Murthy K.S.R.K. A finite element based interior collocation method for the computation of stress intensity factors and T-stresses // Engineering Fracture Mechanics. - 2010. V. 77. №7. - P. 1116-1127). Сравнение экспериментальных, теоретических и расчетных данных приведенных в табл. 2, наглядно демонстрирует, что использование двух первых нечетных коэффициентов рядов (1), полученных по результатам измерений раскрытия в двух точках на берегах трещины, обеспечивает точность определения величин КИН, которая достаточна для большинства инженерных приложений.

Согласно второму подходу величины погрешностей определения КИН оценивают путем построения и визуализации образцовых картин интерференционных полос (Pisarev V.S., Balalov V.V., Aistov V.S., Bondarenko M.M., Yustus M.G. Reflection hologram interferometry combined with hole drilling technique as an effective tool for residual stresses fields investigation in thin-walled structures // Optics & Lasers in Engineering. - 2001. V. 36, №6. - P. 551-597). Для этого используют прямоугольною пластину размерами 120×30×4 мм с центральной симметричной трещиной (а1=2.52 мм; а2=4.59 мм) и такую же пластину без трещины. Упругие постоянные металлической пластины равны E=72000 МПа, μ=0.33. Численное моделирование полей тангенциальных компонент перемещений на поверхности образца проводят на основе программного комплекса MSC/NASTRAN. Конечно-элементную сеть формируют из 100000 элементов типа QUAD 4. Поля перемещений, используемые для визуализации образцовых картин интерференционных полос, определяют вычитанием результатов, полученных для пластины с трещиной и сплошной пластины. На фиг. 8 и фиг. 9 показаны образцовые картины интерференционных полос для тангенциальной компоненты перемещений ν, которые моделируют реальные интерферограммы показанные на фиг. 6 и фиг. 7, соответственно.
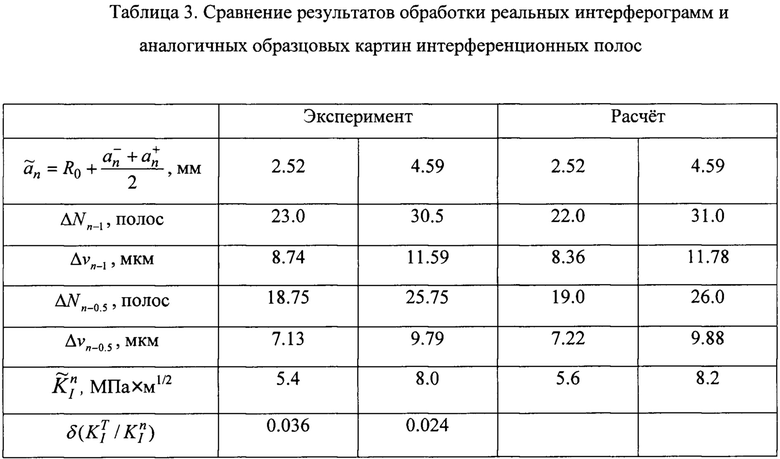
Сравнение экспериментальных параметров, полученных для интерферограмм на фиг. 6 и фиг. 7, и аналогичных данных, которые относятся к соответствующим образцовым картинам интерференционных полос, представлено в табл. 3. Величины разностей абсолютных порядков полос ΔNn-1 и ΔNn-0.5 устанавливают прямым подсчетом, как это показано на фиг. 6 и фиг. 7. Различия этих величин для реальных интерферограмм и соответствующих образцовых картин интерференционных полос находятся в пределах экспериментальной погрешности. Величины компонент перемещений Δνn-1 и Δνn-0.5 в обоих случаях определяют по формуле (11). Наибольшее различие в соответствующих экспериментальных и расчетных величинах составляет 4.3% для раскрытия первой трещины длиной а1=2.52 мм. Данный факт связан с тем, что в эксперименте реальная трещина начинается на контуре отверстия диаметром 2R0=0.5 мм, а моделирование на основе МКЭ проводится для идеальной сплошной трещины. В остальных трех случаях разница между экспериментальными и расчетными величинами не превышает 1.6%. Расчетные величины КИН получают путем использования данных табл. 3 и формулы (10). Данные табл. 3 еще раз подтверждают высокую точность и надежность разработанного метода определения величин КИН.
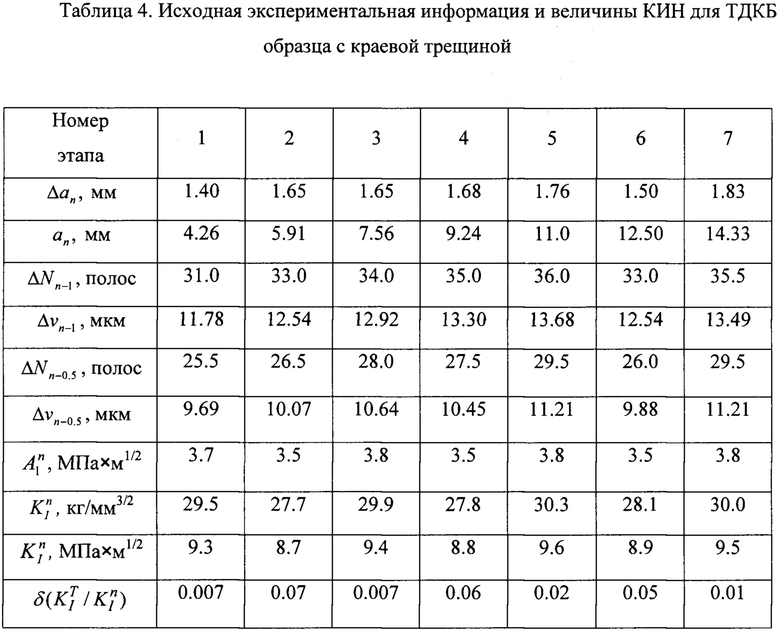
2. Предлагаемым способом проводилось определение КИН для краевой трещины в образце в виде трапецеидальной двухконсольной балки (ТДКБ), чертеж которой показан на фиг. 10. Образец изготовлен из алюминиевого сплава (E=72000 МПа, μ=0.33) и имеет размеры: W=120 мм, е=40.6 мм, Нр=16.43 мм, t=5 мм. Трещина моделируется последовательностью семи узких разрезов шириной Δb=0.3 мм, параметры которых приведены в табл. 4. Исходная длина трещины равна а0=24.7 мм. Образец подвергался внецентренному растяжению с нагрузкой Р=1.52 кН, как это показано на фиг. 10. Интерферограмма, полученная для третьего приращения длины трещины, приведена на фиг. 11. Результаты обработки всех полученных интерферограмм и результаты вычисления КИН по формуле (10) содержатся в табл. 4. Геометрические размеры ТДКБ образца выбраны так, чтобы обеспечить постоянство величины КИН для трещины любой длины. Теоретическая величина КИН для данного образца определяется согласно соотношению, приведенному в разделе 1.14 справочника Мураками (Справочник по коэффициентам интенсивности напряжений: В 2-х томах. Т. 1: Пер. с англ. / Под ред. Ю. Мураками. - М.: Мир, 1990. - 448 с.). Для используемого образца эта величина равна 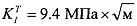 . Последняя строка табл. 4 содержит разницу между экспериментальными и теоретическими величинами КИН, которая не превышает 7%. Данный факт подтверждает высокую точность разработанного подхода в случае исследования краевой трещины.
. Последняя строка табл. 4 содержит разницу между экспериментальными и теоретическими величинами КИН, которая не превышает 7%. Данный факт подтверждает высокую точность разработанного подхода в случае исследования краевой трещины.
3. Предлагаемым способом проводилось определение КИН для трещины, распространяющейся от сварного шва в двух прямоугольных образцах, изготовленных из алюминиевого сплава (E=72000 МПа, μ=0.33). Чертеж образца размерами 180×78×4 мм показан на фиг. 12. Сварной шов изображен заштрихованной областью на фиг. 12. Уникальной особенностью разработанного подхода является возможность определения величин КИН для трещин в поле остаточных напряжений на различных этапах циклического нагружения. Исследование первого образца проводились в исходном состоянии (Образец 1), а второго (Образец 2) после приложения Nm=2506 циклов с параметрами Δσ=300 МПа, R=-l. Одноосное растяжение-сжатие прилагалось вдоль оси у фиг. 12. Остаточные напряжения для обоих образцов определялись в точке 1 с координатами (х=0, у=0) путем совместного применения метода сверления отверстия и электронной спекл-интерферометрии (Pisarev VS, Odintsev IN, Apalkov АА, Chernov AV. Role of high-quality interference fringe patterns for the residual stress determination by the hole-drilling method /Visualization of Mechanical Processes 2011; Vol. 1. N 1. DOI: 10.1615/VisMechProc.v1.i1.40). Малое отверстие диаметром 2r0=1.9 мм, высверленное в точке 1 является исходной точкой дальнейшего распространения трещины в положительном направлении оси х. Величины главных компонент остаточных напряжений равны σ1=-51.2 МПа (направление оси х) и σ2=-170.6 МПа (направление оси у) и σ1=29.6 МПа, σ2=62.3 МПа для образца в исходном состоянии и образца после приложения циклической нагрузки соответственно. Рост трещины в обоих образцах моделируется последовательностью восьми узких разрезов шириной Δb=0.17 мм, как это показано на фиг. 12. Типичные картины интерференционных полос, полученные для второго приращения длины трещины в исходном образце и образце после приложения циклической нагрузки, показаны на фиг. 13 и 14, соответственно. Необходимо отметить высокое качество всех полученных интерферограмм. Симметричная конфигурация полос на фиг. 13 и фиг. 14 по отношению к линии трещины свидетельствует, что трещина распространяется в условиях нормального отрыва. То же самое справедливо для всех длин трещин, исследованных в обоих образцах. Данный факт означает, что величины КИН можно определять согласно формуле (10). Распределение величин раскрытия трещины Δνn-1, (n=1, 2, … , 8) показано на фиг. 15. Зависимости величин КИН от длины трещины приведены на фиг. 16. Сравнительный анализ распределений представленный на фиг. 15 и фиг. 16 демонстрирует перераспределение деформационных и силовых параметров механики разрушения в результате циклического нагружения. Выявлено заметное различие в величинах раскрытия и КИН, несмотря на малое число приложенных циклов. Полученные результаты наглядно демонстрируют уникальные возможности разработанного подхода для исследований эволюции величин КИН для трещин в поле остаточных напряжений при циклическом нагружении.
Приведенные выше оценки погрешностей определений величин КИН, основанные на сравнении экспериментальных, теоретических и расчетных данных, а также на построении образцовых картин интерференционных полос показывают, что эти погрешности не превышают 4% и 7%, для центральной и краевой трещины, соответственно. Такая точность с гарантией достигается в случае, когда разности порядков полос идентифицируются невооруженным глазом оператора, вследствие того, что величина погрешности δN=0.5 полосы означает различие между соседними светлой и темной полосами. Таким образом, предлагаемый способ, который не требует привлечения специального оборудования для автоматической регистрации полей перемещений, обеспечивает точность определения величин КИН для трещин в поле внешних напряжений, достаточную для большинства реальных инженерных задач. Это обеспечивает также применение разработанного подхода для исследования эволюции величин КИН для трещин в поле остаточных напряжений при действии циклического нагружения. Данный факт является уникальной особенностью модифицированной версии метода ПНДТ, который обеспечивает получения новых данных, недоступных для традиционных методов исследования подобных задач.
Этот технический результат достигается за счет того, что при способе определения коэффициентов интенсивности напряжений для трещин в поле внешних и остаточных напряжений, включающем регистрацию спекл-структуры на поверхности образца в исходном состоянии высокоразрешающей видеокамерой, увеличение длины трещины на малое приращение, регистрацию спекл-структуры деформированной поверхности образца вследствие продвижения трещины, визуализацию картин интерференционных полос путем численного вычитания двух полученных ранее изображений, определение величин раскрытия трещины в точке начала приращения ее длины и в центральной точке этого приращения, при этом вычисление величин КИН осуществляется по формулам, вытекающим из представления поля перемещений в окрестности вершины трещины на основе бесконечных рядов Уильямса, что исключает необходимость численного моделирования при переходе от измеряемых параметров к величинам КИН и тем самым обеспечивает существенное повышение точности и надежности результатов определения КИН.
Технический результат достигается также наличием деформационных компонент перемещений, измеренных непосредственно на берегах трещины при малом приращении ее длины, что повышает точность определения КИН. Это связано с тем, что картины интерференционных полос, зарегистрированные непосредственно в окрестности вершины трещины, служат надежным индикатором типа напряженного состояния и, следовательно, обоснованности использования расчетных формул. Кроме того, разработанный метод универсален по отношению, как к геометрической форме и материалу исследуемой конструкции, так и к этапу циклического нагружения. Таким образом, разработанный подход обеспечивает новый качественный уровень получения результатов, которые необходимы для надежного описания процесса распространения усталостной трещины в окрестности сварного шва.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ | 2014 |
|
RU2574231C1 |
| КОМПЬЮТЕРНО-РЕАЛИЗУЕМЫЙ СПОСОБ ОЦЕНКИ СРОКА СЛУЖБЫ ИМЕЮЩЕЙ ТРЕЩИНУ ДЕТАЛИ И СИСТЕМА ДЛЯ ОЦЕНКИ СРОКА СЛУЖБЫ ДЕТАЛИ | 2017 |
|
RU2748411C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕОДНОРОДНЫХ ПОЛЕЙ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ПЛОСКИХ ДЕТАЛЯХ | 2022 |
|
RU2811396C1 |
| СПОСОБ ОЦЕНКИ ПРОЧНОСТИ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ | 1999 |
|
RU2186361C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ ДЛЯ ТРЕЩИНЫ В КОНСТРУКЦИИ | 2021 |
|
RU2773260C1 |
| Способ контроля прочности оптического волокна | 2021 |
|
RU2762885C1 |
| Способ контроля прочности оптического волокна | 2020 |
|
RU2743737C1 |
| Способ неразрушающего контроля прочности оптического волокна | 2021 |
|
RU2758340C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 1991 |
|
RU2032162C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВНУТРЕННИХ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2019 |
|
RU2712929C1 |


Изобретение относится к области экспериментальной механики и предназначено для определения коэффициентов интенсивности напряжений (КИН) для трещин, возникающих при эксплуатации элементов авиационных конструкций. Сущность: осуществляют установку исследуемого образца, нагруженного внешними усилиями и/или содержащего остаточные напряжения, в оптическую схему интерферометра, регистрацию исходного состояния спекл-структуры поверхности высокоразрешающей видеокамерой, увеличение длины трещины на малое приращение, регистрацию спекл-структуры деформированного состояния поверхности образца вследствие продвижения трещины, визуализацию картин интерференционных полос путем численного вычитания двух полученных ранее изображений, определение величин раскрытия трещины в точке начала приращения ее длины и в центральной точке этого приращения, вычисления величины КИН по формулам, вытекающим из соотношений линейной механики разрушения. Технический результат: повышение точности измерения КИН при воздействии внешних и, особенно, остаточных напряжений, что необходимо для повышения эксплуатационного ресурса и надежности элементов авиационных конструкций за счет учета эволюции параметров механики разрушения вследствие циклического нагружения. 1 з.п. ф-лы, 4 табл., 16 ил.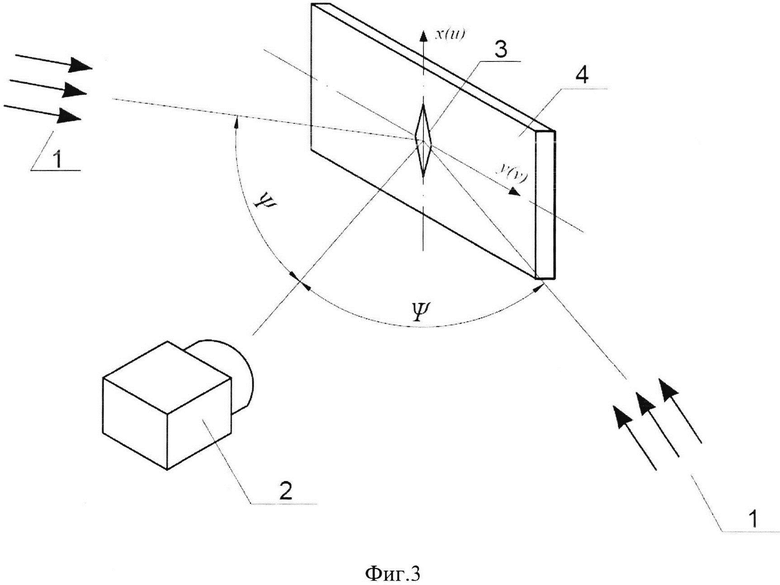
1. Способ определения коэффициентов интенсивности напряжений для трещин, включающий установку образца, увеличение длины трещины на малое приращение с помощью разреза и измерение деформационного отклика, отличающийся тем, что образец устанавливают в оптическую схему интерферометра, регистрируют исходное состояние спекл-структуры поверхности видеокамерой, после увеличения длины трещин регистрируют спекл-структуру деформированного состояния поверхности образца, визуализируют картину интерференционных полос на основе полученных изображений, определяют раскрытие трещины в точке начала приращения ее длины и в центральной точке этого приращения и определяют величину коэффициента интенсивности напряжений для трещины длиной an расчетным методом.
2. Способ по п.1, отличающийся тем, что в качестве расчетного метода используют формулу

где Е - модуль упругости материала; Δan - приращение длины трещины; Δνn-1 - величина раскрытия трещины в точке начала приращения ее длины n-1; Δνn-0.5 - величина раскрытия трещины в центральной точке приращения ее длины n-0.5.
| СПОСОБ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОГО КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ НАПРЯЖЕНИЯ В ИЗДЕЛИИ | 2006 |
|
RU2324916C1 |
| СПОСОБ ОЦЕНКИ ПРОЧНОСТИ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ | 1999 |
|
RU2186361C2 |
| Способ диагностики усталостного разрушения детали | 1990 |
|
SU1744583A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ | 2014 |
|
RU2574231C1 |
| US 7884924 B2, 08.02.2011. | |||
Авторы
Даты
2018-09-18—Публикация
2017-10-25—Подача