Изобретение относится к области оптики и может быть использовано для характеристики качества световых пучков, формируемых оптическими элементами и системами. Определение деформаций волнового фронта таких пучков позволяет судить о качестве изготовления оптических элементов и систем.
Реальные оптические элементы и системы всегда вносят те или иные искажения в волновой фронт проходящих через них световых пучков. Причинами возникновения искажений, как правило, являются погрешности изготовления оптических элементов и систем. На финальной стадии полировки и точной доводки больших поверхностей часто используется доводочный инструмент малых размеров, действующий зонально. В результате на оптической поверхности элемента остаются мелкомасштабные или, как их называют, волнистые деформации профиля, которые порождают деформации волнового фронта светового пучка, прошедшего оптический элемент. По аналогии и в связи с природой происхождения далее такие деформации поверхности волнового фронта будут называться волнистыми деформациями волнового фронта светового пучка. Критерием, разделяющим волнистые и крупномасштабные деформации (или деформации формы) поверхности оптического элемента относительно идеального профиля, считают пространственную частоту гармоник деформаций поверхности на уровне 5 периодов и более на длине радиуса оптического элемента, взятой в качестве базовой [Проектирование оптических систем. Под ред. Р. Шеннона, Дж. Вайнта. М.: Изд-во Мир. 1983. - 432 с.]. Аналогичным образом можно характеризовать и волнистые деформации волнового фронта светового пучка, порожденные волнистыми деформациями поверхностей оптических элементов и систем, рассматривая в качестве базовой длины радиус светового пучка.
Далее нами будут рассматриваться способы определения волнистых деформаций светового пучка по всей апертуре оптической системы. Несмотря на значимость этой проблемы, сведения, характеризующие уровень техники в данной области измерений, практически отсутствуют. Особенно важно иметь информацию о распределении волнистых деформаций по всему сечению искаженного пучка для крупногабаритных оптических систем.
К точности определения волнистых деформаций предъявляются достаточно высокие требования. Волнистые деформации оптических поверхностей, и, соответственно, волнистые деформации волнового фронта светового пучка, как правило, имеют значения вплоть до нескольких единиц нанометров. Известны классы оптических систем, для которых и такой низкий уровень деформаций волнового фронта является критическим. Это космические телескопы, работающие в диапазоне длин волн от 0.12 мкм (α-линия серии Лаймана λ=121,5 нм) [Jones C.O. Space telescope optics. Optical engineering. 1979, v. 18, №3, p. 273-280], а также объективы, используемые в аппаратуре нанолитографии, оптимальный диапазон для которых лежит в области вакуумного ультрафиолета - 13,4 нм [В.К. Кирилловский, Е.В. Гаврилов. Оптические измерения. Ч. 7. Инновационные методы контроля при изготовлении прецизионных асферических поверхностей. СПб ГУ ИТМО. 2009. - 118 с.].
Еще один важный класс оптических элементов, где декларируются жесткие требования к оптическому качеству, это дисковые активные элементы (так называемые «слэбы») усилительных каналов многоканальных лазерных систем на неодимовом стекле для решения задач управляемого термоядерного синтеза [О.И. Шанин. Адаптивные оптические системы в импульсных мощных лазерных установках. М: Техносфера. 2012. - 200 с.]. В мощном усилительном канале лазера искажения волнового фронта светового пучка, включая волнистые деформации, провоцируют развитие мелкомасштабной самофокусировки излучения, приводящей к катастрофическому разрушению активной среды лазера.
К наиболее точным способам измерения формы волнового фронта по всему поперечному сечению светового пучка относятся интерферометрические. Результатом интерферометрических измерений является экспериментально обнаруживаемая разность хода интерферирующих волн, которая выражается в долях длины волны излучения λ, используемого в интерферометре. Минимальную зарегистрированную разность хода, обнаруживаемую в поперечном сечении контролируемого пучка, можно считать наименьшей регистрируемой деформацией волнового фронта контролируемого пучка, выраженной в долях λ. Значение этой величины будет характеризовать точность способа измерения деформации волнового фронта. Аналогичным образом можно ввести наименьшую волнистую деформацию волнового фронта контролируемого пучка wмин, выраженную в долях λ, регистрируемую в поперечном сечении контролируемого пучка.
Рассмотрение интерферометрических способов измерения деформаций волнового фронта показывает, что наименее чувствительными к влиянию внешних помех, таких, как вибрации и неоднородные воздушные потоки в месте проведения измерений, являются способы, в которых оптические пути опорного и искаженного контролируемого пучка на значительном участке схемы формирования пучков совпадают. В этом случае одинаковые ошибки фронта, набранные пучками на общих участках схемы, при интерференции пучков вычитаются. Такой принцип формирования интерферирующих пучков был предложен Физо.
Известен способ определения деформаций волнового фронта светового пучка, основанный на применении этого принципа [Optical Shop Testing. Ed. D. Malacara. New York. J. Willy and Sons Inc. 1992. 773 p.] В способе формируют гомоцентрический лазерный пучок с применением точечной диафрагмы, пропускают его через коллимирующий объектив и светоделитель, затем направляют на эталонный оптический элемент и на установленную за ним контролируемую оптическую систему. В результате отражения части исходного пучка от рабочей поверхности эталона формируется опорная волна, а после прохождения оставшейся части исходного пучка контролируемой оптической системы формируется искаженная системой волна, деформации которой определяются. Обе волны, имеющие за счет схемного решения согласованную кривизну волнового фронта, направляют по общей части оптического тракта в обратном направлении, т.е. к источнику излучения. На этом проходе светоделитель отводит пучки в канал регистрации интерференционной картины, который включает в себя, как правило, проекционный объектив и матричный фотоприемник. Сформированную в плоскости фотоприемника (ПЗС матрицы) интерференционную картину в виде чередующихся светлых и темных полос регистрируют в виде цифрового изображения. Далее с использованием соответствующих математических соотношений и алгоритмов обработки данных по искривлениям гребней полос рассчитывают таблицу значений или карту распределения величин деформаций волнового фронта по сечению пучка.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относятся следующие. Известный способ требует для формирования опорного волнового фронта применения высокоточного оптического эталона и когерентного лазерного источника излучения, отличается относительной сложностью оптической схемы, подвержен воздействию когерентных шумовых помех, ограничен в точности измерений деформаций волнового фронта.
Поскольку интерферограмму формируют в когерентном свете, то так называемый «когерентный» шум, включающий в себя зернистость распределения интенсивности (спеклы) и неоднородности распределения интенсивности за счет выбросов интенсивности, обусловленных пылью, дефектами и паразитными бликами оптических поверхностей интерферометра, «впечатывается» в интерференционную картину. Этот шум ограничивает точность определения близких по масштабу локальных искривлений интерференционных полос, вызванных волнистыми деформациями волнового фронта. При этом число интерференционных полос на диаметре пучка должно быть достаточным для пространственного разрешения мелкомасштабных волнистых деформаций.
Измеренные деформации волнового фронта неизбежно включают в себя, в том числе, деформации волнового фронта, внесенные самим эталонным элементом в опорную волну. Наименьшая регистрируемая деформация волнового фронта контролируемого пучка с учетом качества изготовления рабочей поверхности типового эталона составляет величину wмин=λ/25 в лучшем случае.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения волнистых деформаций волнового фронта по всему сечению светового пучка, реализованный в схеме высокоточного интерферометра типа Intellium Н2000 (производитель фирма ESDI, США) [Н.В. Барышников, Я.В. Гладышева, Д.Г. Денисов, И.В. Животовский, В.Е. Патрикеев, И.Н. Судариков. Вестник МГТУ им. Н.Э. Баумана. Сер. «Приборостроение», 2012, с. 4-16]. При реализации способа формируют два наклоненных под небольшим углом друг к другу когерентных гомоцентрических лазерных пучка с ортогональными поляризациями, оба пучка пропускают через коллимирующую систему, включающую пространственный фильтр, затем пучки направляют на эталонный оптический элемент и на установленную за ним контролируемую оптическую систему. Лазерные пучки частично отражаются от рабочей поверхности эталона и от поверхности контролируемой оптической системы, которые наклонены таким образом, чтобы только отраженные опорная и искаженная волны с заданными ортогональными поляризациями шли в обратном направлении параллельно оптической оси интерферометра. Остальные отраженные волны блокируются пространственным фильтром в фокальной плоскости интерферометра. После прохождения пространственного фильтра искаженный и опорный пучки с ортогональными поляризациями поступают в трехканальное поляризационное устройство фазового сдвига с ПЗС-матрицами на выходе каналов. Это устройство синхронно формирует и регистрирует три интерференционные картины, отличающиеся величиной фазового сдвига опорной волны относительно искаженной. Далее для определения искомых деформаций волнового фронта численным методом используют математическое соотношение, связывающее разность фаз искаженной и опорной волн в каждой точке поперечного сечения светового поля с алгебраической комбинацией значений интенсивности, зарегистрированных в той же точке в каждой из трех интерферограмм. Выполненная в соответствии соотношением совместная обработка трех интерферограмм, полученных с разным фазовым сдвигом между опорной и искаженной волной, позволяет определить деформации волнового фронта в каждой точке поперечного сечения пучка.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относятся сложность реализации, высокая трудоемкость, наличие ограничений в точности определения деформаций волнового фронта. Используемая оптическая схема отличается сложностью, высокими требованиями к точности юстировки ее элементов и чувствительностью результатов к воздействию шумовых и фазовых помех. Точная настройка и юстировка всех элементов схемы, прецизионные измерения одновременно трех интерферограмм и их последующая совместная обработка существенно увеличивают трудоемкость процесса определения деформаций искаженного волнового фронта. Реализация способа требует применения прецизионно изготовленных оптического эталона и трехканального поляризационного светоделителя, а также высококогерентного лазерного источника поляризованного излучения. Опорный волновой фронт должен строго отвечать по общей конфигурации (плоская, сферическая) искаженному волновому фронту, т.е. эталонный элемент, оптический или голографический, нужно специально изготавливать под каждую оптическую систему, подлежащую измерению. Это усложняет процедуру определения деформаций волнового фронта.
Следует также иметь ввиду, что при измерении характеристик оптической системы, работающей на пропускание (слэб, объектив), необходимо строить автоколлимационную схему с применением дополнительного согласованного по кривизне поверхности прецизионного отражающего зеркала. При этом регистрируются деформации волнового фронта, внесенные в пучок оптической системой совокупно на прямом и обратном проходе через нее. Такие результаты не дают точной характеристики деформаций волнового фронта пучка, вносимых оптической системой в рабочем, т.е. в однопроходовом режиме.
Теоретически при реализации этого способа когерентные шумы в интерференционной картине подавляются, но только если распределения выбросов интенсивности во всех трех интерферограммах совпадают попиксельно и по величине интенсивности. Однако очевидно, что такое полное совпадение распределений интенсивности когерентных шумов в трех интерферограммах маловероятно. Аналогично и присущие самой ПЗС-матрице шумовые выбросы интенсивности в пикселях, статистически распределенные по ее сечению, будут различны в трех разных ПЗС-матрицах. Все эти шумы будут суммарно вносить вклад в ошибку измерений волнового фронта. Дополнительными источниками ошибок будут неконтролируемые изменения фазового сдвига между интерферирующими пучками в трех каналах регистрации, обусловленные погрешностями схемы, а также остаточное влияние неоднородных воздушных потоков, локализованных в зазоре между эталонным элементом и контролируемой оптической системой. Применяемые методы сглаживания интерференционной картины, устраняющее указанные шумы, практически не приемлемы, поскольку сглаживание будет отфильтровывать и информацию об измеряемых мелкомасштабных волнистых деформациях волнового фронта.
В результате все эти выше упомянутые факторы не позволяют определить способом-прототипом волнистые деформации волнового фронта точнее, чем характеризуемые значениями wмин=λ/50. Измеренные деформации волнового фронта включают в себя также деформации, внесенные в опорную волну эталонным элементом. В рекламной информации производителей интерферометра Intellium Н2000 в сети «Интернет» сообщается о достижении наименьшего регистрируемого значения деформации контролируемого волнового фронта на уровне λ/100. Это значение достигается лишь за счет повышения точности изготовления эталона, позволяющего сформировать опорную волну еще более высокого качества.
Сущность изобретения заключается в следующем.
Задачей изобретения является определение деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, с высокой точностью, простотой реализации и меньшей трудоемкостью.
Технический результат, который достигается при осуществлении заявленного способа, заключается в определении деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, с высокой точностью при существенном упрощении процесса измерений и уменьшении его трудоемкости.
Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, включающем направление гомоцентрического светового пучка с длиной волны λ на оптическую систему, получение математического выражения для определения деформаций волнового фронта светового пучка, определение деформаций волнового фронта светового пучка путем решения численным методом полученного математического выражения, в соответствии с заявляемым техническим решением световой пучок, направляемый на оптическую систему, формируют некогерентным, определяют положение плоскости Пмакс, перпендикулярной оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, в которой пиковая интенсивность светового пучка в изображении поперечного сечения светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измеряют диаметр D светового пучка в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, измеряют расстояние Lмакс по оси пучка от плоскости Пмакс до плоскости П с учетом правила знаков, регистрируют распределение интенсивности I(u,v) светового пучка в координатах (u,v) плоскости Ппр, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие |Lпр|=103⋅λ⋅(Lмакс/D)2, где Lпр - расстояние по оси пучка от плоскости Пмакс до плоскости Ппр с учетом правила знаков, определяют функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл], где I(u,v)сгл - распределение интенсивности I(u,v), сглаженное с использованием метода наименьших квадратов, выполняя разложение функции ψ(u,v) в двумерный тригонометрический ряд Фурье, получают двумерный амплитудный спектр гармоник ряда Фурье, находят порядковый номер μмакс наивысшей из гармоник ряда Фурье, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник, регистрируют распределение интенсивности Iрег(ξ,η) светового пучка в координатах (ξ,η) плоскости Прег, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие |Lрег|=4⋅λ⋅(μмакс⋅Lмакс/D)2, где Lрег - расстояние по оси пучка от плоскости Пмакс до плоскости Прег с учетом правила знаков, при этом начало координат в плоскостях П, Прег, Ппр, Пмакс лежит на оси светового пучка, математическое выражение для определения деформаций волнового фронта светового пучка w(x,y), вызванных волнистостью поверхностей оптической системы, определяют в виде уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
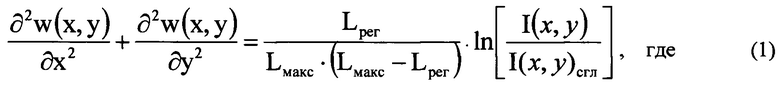
- I(х,у) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности Iрег(ξ,η) по формулам ξ=х⋅(Lрег/Lмакс) и n=у⋅(Lpег/Lмакс);
- I(х,у)сгл - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка I(х,у);
значения w(x,y) определяют путем численного решения уравнения (1) вариационным методом при свободных граничных условиях, аппроксимируя w(x,y) тригонометрическим полиномом, состоящим из суммы из членов двумерного ряда Фурье с порядковыми номерами гармоник μх и μу, пробегающими диапазон от 1 до μмакс, за исключением тех членов ряда, для которых оба порядковых номера μх и μу имеют значения, меньшие 10.
Совокупность вышеизложенных признаков изобретения связана причинно-следственной связью с техническим результатом изобретения.
Гомоцентрический световой пучок после прохождения несовершенной оптической системы приобретает деформации его волнового фронта. Эти деформации по мере распространения светового пучка в пространстве изображений приводят к возникновению неоднородностей в распределении интенсивности по поперечному сечению пучка. Количественная взаимосвязь между деформациями волнового фронта и проявляющимися неоднородностями в распределении интенсивности сфокусированного пучка определялась нами в рамках геометрооптического приближения [Татарский В.И. Распространение волн в турбулентной атмосфере. М., изд-во "Наука". - 1979. - 328 с.].
В заявляемом техническом решении волнистые деформации волнового фронта светового пучка w(x,y), вызванные волнистыми деформациями поверхностей оптической системы, определяют в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы. Для расчета указанных деформаций используют результаты измерений распределения интенсивности искаженного светового пучка в плоскости, перпендикулярной оси светового пучка в пространстве изображений, Прег, положение которой выбирают определенным образом.
Выбор положения плоскости Прег в пространстве изображений существенно влияет на точность решения поставленной задачи. Чем дальше от плоскости П плоскость Прег, в которой осуществляются измерения распределения интенсивности искаженного светового пучка, тем сильнее выражены неоднородности распределения интенсивности, и тем точнее их можно измерить на фоне шумов. В то же время по мере удаления светового пучка от оптической системы в проявлениях неоднородностей распределения интенсивности в поперечном сечении пучка начинает сказываться волновая природа светового поля из-за нарушений условий геометрооптического приближения. Вследствие этого на волновом фронте пучка на выходе оптической системы каждому лучу следует адресовать не просто точку исхода, а некоторый окружающий точку участок волнового фронта, так называемую зону Френеля, размер которой растет по мере удаления от оптической системы.
Проведенный нами анализ показал, что если диаметр зоны Френеля не превышает пространственный период волнистых деформаций волнового фронта в плоскости П, то геометрооптическое приближение еще остается справедливым для рассмотрения распространения светового пучка до плоскости Прег. В противном случае, т.е. при диаметре зоны Френеля, превышающем пространственный период волнистых деформаций, усредненное по зоне Френеля действие деформаций волнового фронта приводит к сглаживанию возникших неоднородностей в распределении интенсивности светового пучка в плоскости Прег.
Согласно введенному нами условию, положение плоскости Прег выбирается так, что диаметр зоны Френеля в плоскости П не превышает пространственный период любой из гармоник, присутствующих в спектре волнистых деформаций волнового фронта. Тогда наибольшее удаление плоскости Прег от оптической системы, еще возможное в рамках справедливости геометрооптического приближения, имеющее следствием достижение наибольшего контраста проявившихся неоднородностей в распределении интенсивности светового пучка, отвечает условию, при котором диаметр зоны Френеля достигает, но не превышает пространственного периода наивысшей гармоники из присутствующих в спектре волнистых деформаций волнового фронта.
В заявляемом техническом решении порядковый номер наивысшей гармоники из присутствующих в спектре волнистых деформаций волнового фронта определяют из рассмотрения пространственных гармоник неоднородностей, проявляющихся в распределении интенсивности искаженного светового пучка, распространяющегося в пространстве изображений.
Осуществляют это следующим образом. Определяют положение плоскости Пмакс в которой пиковое значение интенсивности в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, достигает максимального значения Iмакс. Измеряют диаметр светового пучка D в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы. Далее определяют расстояние Lмакс от плоскости Пмакс до плоскости П, используя при этом систему отсчета, задаваемую системой координат в плоскости Пмакс, в которой начало координат лежит на оси светового пучка, а положительное направление оси аппликат совпадает с направлением распространения светового пучка.
Проведенные нами расчеты показали, что при наличии в световом пучке волнистых деформаций волнового фронта соответствующие неоднородности распределения интенсивности гарантированно проявляются в изображениях поперечных сечений светового пучка на расстоянии Lпр от плоскости Пмакс либо по ходу пучка, либо в обратном направлении, при этом значение |Lпр|=103⋅λ⋅(Lмакс/D)2. Выбирая плоскость Ппр на расстоянии Lпр от плоскости Пмакс в том или ином направлении, регистрируют в ней распределение интенсивности светового пучка I(u,v), где u и v координаты в плоскости Ппр. Далее определяют функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл,], где I(u,v)сгл - распределение интенсивности в поперечном сечении пучка, сглаженное методом наименьших квадратов. При выполнении операции сглаживания применяют стандартную процедуру аппроксимации функции I(u,v)сгл двумерными полиномами того или иного вида. Функция ψ(u,v) является своеобразным индикатором присутствия волнистых деформаций волнового фронта, поскольку в их отсутствие близка к нулю по всему сечению пучка. Затем выполняют разложение функции ψ(u,v) в двумерный тригонометрический ряд Фурье, получают двумерный амплитудный спектр гармоник ряда Фурье, находят порядковый номер μмакс наивысшей из гармоник ряда Фурье, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник. Полученное значение μмакс и будет соответствовать порядковому номеру наивысшей из пространственных гармоник неоднородностей, проявляющихся в распределении интенсивности искаженного светового пучка
Найденное значение μмакс позволяет определить положение плоскости Прег. В соответствии с заявляемым техническим решением плоскость Прег должна отстоять от плоскости Пмакс на расстояние |Lрег|=4⋅λ⋅(μмакс⋅Lмакс/D)2 либо по ходу пучка, либо в обратном направлении. Данное соотношение для положения плоскости Прег основано на вычислении размеров зон Френеля для точек изображения светового пучка в плоскости Прег и выполнении указанного выше условия: диаметр зоны Френеля в плоскости П не должен превышать пространственный период гармоники с порядковым номером μмакс.
Как показали наши эксперименты и проведенное имитационное математическое моделирование, такое определение положения плоскости Прег является оптимальным для выполнения условий справедливости геометрооптического приближения с учетом наивысшей гармоники из присутствующих в спектре волнистых деформаций волнового фронта светового пучка на выходе оптической системы и достижения наибольшего контраста неоднородностей в распределении интенсивности светового пучка.
Определив положение плоскости Прег, регистрируют распределение интенсивности Iрег(ξ,η) светового пучка в координатах (ξ,η) плоскости Прег. Начало координат в плоскостях П, Прег, Ппр, Пмакс лежит на оси светового пучка. Выбор положения плоскостей Ппр и Прег от плоскости Пмакс либо по ходу пучка, либо в обратном направлении равнозначен и зависит лишь от конструктивных особенностей конкретных схем измерения распределения интенсивностей светового пучка.
С использованием волнового уравнения, описывающего распространение прошедшего оптическую систему и сфокусированного в пространстве изображений светового пучка, в приближении геометрической оптики нами было получено соотношение (1), связывающее деформации волнового фронта светового пучка w(x,y), вызванные волнистостью поверхностей оптической системы, т.е. волнистые деформации волнового фронта, в координатах (х,у) плоскости П с распределением интенсивности светового пучка в плоскости Прег.
Для реализации способа световой пучок, прошедший оптическую систему, должен быть сфокусирован в пространстве изображений. Если оптическая система не фокусирует сама световой пучок в пространстве изображений, осуществляют его фокусировку с помощью безаберрационных оптических элементов. Подходы к решению этой задачи известны [Э.А. Витриченко. Методы исследования астрономической оптики. М.: Изд-во Наука. 1980. - 152 с.]. Уточним здесь также, что понятие прохождения светового пучка через контролируемую оптическую систему подразумевает как случаи непосредственного прохождения пучка через оптическую систему, так и случаи отражения светового пучка от нее.
Вычисление волнистых деформаций волнового фронта выполняют, используя вариационный метод, основанный на поиске минимума функционала, отвечающего уравнению вида (1). Варианты этого метода (метод Ритца или метод Галеркина) позволяют найти с высокой точностью устойчивые решения уравнений такого типа [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М. - Л.: Гос. Изд-во физ. - мат. лит. 1962. - 708 с.].
Согласно этому методу решение ищут в виде суммы функций 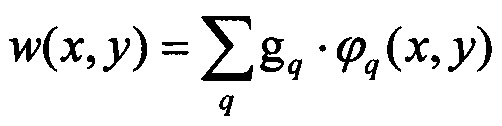 с неопределенными коэффициентами gq, численные значения которых, дающие решение, определяются из условия минимума функционала. Находят минимум при свободных граничных условиях [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М. - Л.: Гос. Изд-во физ. - мат. лит. 1962. - 708 с.].
с неопределенными коэффициентами gq, численные значения которых, дающие решение, определяются из условия минимума функционала. Находят минимум при свободных граничных условиях [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М. - Л.: Гос. Изд-во физ. - мат. лит. 1962. - 708 с.].
Аппроксимируют w(x,y) тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник μх и μу:
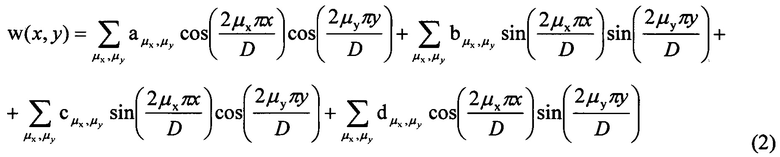
Значения коэффициентов в тригонометрическом полиноме определяют из условия минимума функционала, отвечающего уравнению (1) [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М. - Л.: Гос. Изд-во физ. - мат. лит. 1962. - 708 с.], откуда следует:
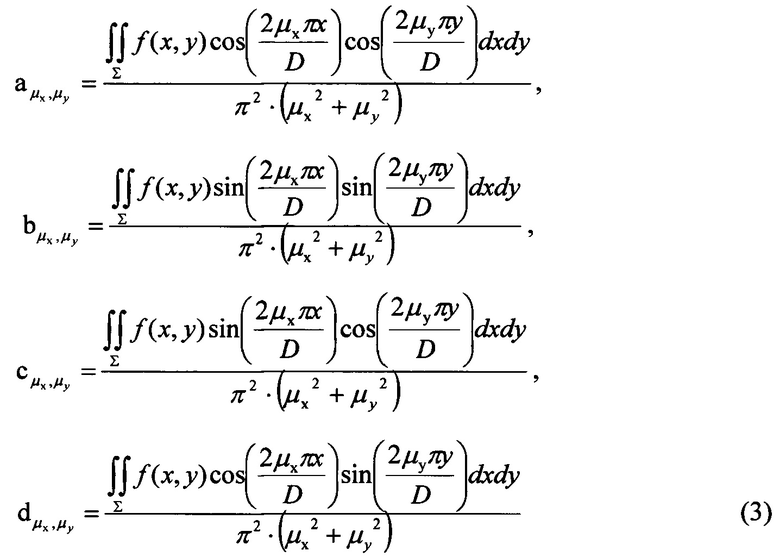
Здесь ƒ(x,y) - это правая часть уравнения (1), т.е. ƒ(х,у)=[Lрег/Lмакс⋅(Lмакс-Lрег)]⋅ψ(х,у), где ψ(х,у)=ln[I(х,у)/I(х,у)сгл], область интегрирования Σ - есть поперечное сечение пучка. Порядковые номера гармоник μх и μу пробегают диапазон от 1 до максимального значения μмакс, но при этом члены ряда, для которых оба порядковых номера μх и μу имеют значения, меньшие 10, должны быть исключены из суммы ряда. Последнее обстоятельство связано с тем, что, согласно введенному выше определению, к волнистым деформациям волнового фронта относятся гармоники, имеющие пять периодов искажений и более на радиусе светового пучка (или 10 периодов на диаметре светового пучка D в нашем случае).
В результате применения способа значения деформаций волнового фронта светового пучка определяют в виде распределения значений w(x,y) в координатах (х,у) поперечного сечения светового пучка. Исходя из этого, полученные результаты могут быть представлены различным образом. В числовом виде значения w(x,y) образуют трехмерный массив числовых данных. На его основе можно создать несколько вариантов графического представления полученных значений w(x,y). Этими вариантами являются следующие. Во-первых, представление распределения деформаций волнового фронта в виде полутонового изображения, в котором яркость элемента изображения (пиксела) отвечает величине деформации. В другом варианте распределение деформаций волнового фронта можно представить в виде системы изолиний с заданным шагом между уровнями деформаций волнового фронта. Также распределение деформаций волнового фронта можно представить в виде в виде объемного графика распределения деформаций волнового фронта по поперечному сечению пучка. Помимо этого, из полученных данных можно определить стандартные числовые характеристики волнового фронта, такие как среднеквадратичное значение или расстояние между экстремальными значениями волнистых деформаций волнового фронта в пределах поперечного сечения пучка, и другие характеристики.
Как видно, заявляемый способ достаточно прост в реализации. Математическое соотношение для определения волнистых деформаций волнового фронта светового пучка включает минимальное число параметров, измеряемых экспериментально. Оптическая схема и технические средства, используемые в эксперименте, существенно проще применяемых в способе-прототипе, для реализации которого необходимы трехканальный поляризационный фазосдвигающий делитель с прецизионно сопряженными взаимно ПЗС-камерами на выходе каналов, высокоточный эталон для формирования опорного пучка, одночастотный стабилизированный лазер и т.д. В силу использования в способе некогерентного источника света существенно снижается по сравнению с прототипом влияние вибраций и неоднородных потоков воздуха на точность получаемых результатов. Отсутствуют также шумы в виде спекл-структуры в распределении интенсивности, присущие когерентным источникам света.
Оценим предельную точность измерений деформаций волнового фронта при реализации заявляемого способа. Для этого введем в рассмотрение относительную величину интенсивности пространственного шума на приемной площадке фотоприемника δ=(Iш/<I>), где Iш - случайные значения интенсивности шума, а <1> - среднее значение интенсивности в зарегистрированном изображении. Дисперсию этой величины обозначим как σδ2 и при выполнении оценок учтем, что отношение (сигнал/шум), характеризующее качество фотоприемника, определяется величиной (σδ)-1. В отсутствие внешних помех шумы в обрабатываемом изображении обусловлены свойствами фотоприемного устройства. В свою очередь, дисперсию значений функции ψ(x,y), характеризующей неоднородности в распределении интенсивности светового пучка в плоскости П и несущей информацию о волнистых деформациях волнового фронта, обозначим σ2ψ. Как показало проведенное нами математическое моделирование, относительная погрешность определения величины волнистых деформаций волнового фронта находится в пределах 10%, если дисперсия σ2ψ превышает σ2δ в десять и более раз, т.е. σ2ψ≥10⋅σ2δ. Исходя из этого, можно оценить наименьшее значение волнистых деформаций wмин, определяемое с относительной погрешностью в пределах 10%.
Пусть волнистые деформации волнового фронта w(x,y) имеют вид суммы пространственных гармоник с амплитудой Q и числом периодов, укладывающихся на диаметре пучка D, равным m:
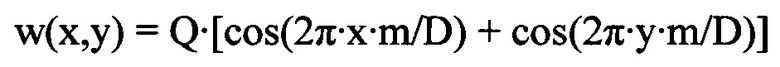
При расчетах учтем, что для этих гармоник деформаций следует выбирать |Lрег|=4⋅λ(Lмакс⋅m/D)2, поскольку в данном случае μмакс=m. Наименьшая величина регистрируемой деформации волнового фронта контролируемого пучка будет соответствовать в рамках нашего способа наименьшей величине неоднородностей в распределении интенсивности по сечению пучка I(х,у) с периодом D/m. Подставляя w(x,y) в левую часть уравнения (1) и учитывая приведенное выше соотношение для |Lрег|, после небольших преобразований и упрощений получим уравнение, связывающее в отсутствие шумов величины неоднородностей в распределении интенсивности с параметрами волны деформаций волнового фронта в виде:
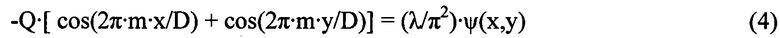
Вычисляем дисперсию левой части соотношения (4), что дает нам величину дисперсии волнистых деформаций волнового фронта σ2w=Q2 и связанную с ней линейно величину дисперсии 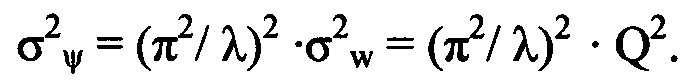
Примем, что шумы, обусловленные свойствами фотоприемного устройства, характеризуются среднеквадратичным значением σδ=10-2.5, отвечающем нижней границе характерных для ПЗС-камер значений сигнал/шум на уровне 50 дБ.
Выше отмечалось, что определить волнистые деформации с относительной погрешностью в пределах 10% можно при условии σ2ψ≥10⋅σ2δ. Из этого выражения при равенстве его левой и правой части находим соотношение для наименьшего определяемого с погрешностью в пределах 10% значения амплитуды волнистых деформаций волнового фронта wмин=Qмин:
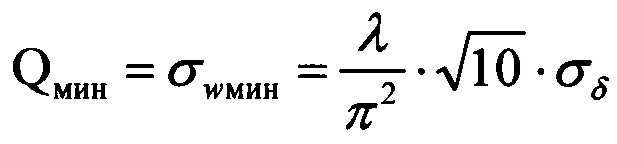
Отсюда следует, что при относительном уровне шума σδ=10-2.5 минимальные определяемые значения волнистых деформаций составляют величину wмин=Qмин=σwмин=λ/1000.
Таким образом, совокупное действие всех признаков изобретения позволяет определить волнистые деформации волнового фронта по всему поперечному сечению светового пучка с высокой точностью, вплоть до уровня значений λ/1000 с относительной погрешностью в пределах 10%, при существенном упрощении эксперимента и уменьшении его трудоемкости.
На фиг. 1 приведена оптическая схема установки для измерения волнистых деформаций волнового фронта светового пучка, вызванных волнистыми деформациями поверхности параболического зеркала, где 1 - некогерентный источник излучения (лампа накаливания);2 - объектив конденсора; 3 - узкополосный светофильтр; 4 - микродиафрагма; 5 - длиннофокусное зеркало коллиматора, 6 - параболическое зеркало; 7 - ПЗС-матрица, регистрирующая распределение интенсивности в поперечном сечении светового пучка. Плоскость П, в системе координат которой определяют волнистые деформации волнового фронта пучка, ортогональна оптической оси светового пучка и соприкасается с оптической поверхностью зеркала 6, плоскость Прег - плоскость, в которой регистрируют распределение интенсивности Iрег(ξ,η), плоскость Пмакс - плоскость, в которой достигает максимального значения 1 макс пиковое значение распределения интенсивности излучения в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка. Плоскости Ппр, Прег и Пмакс ортогональны оси светового пучка, Lпр, Lрег, Lмакс - расстояния от плоскости Пмакс до плоскостей Ппр, Прег и П, соответственно, по оси пучка с учетом правила знаков. Начало координат в плоскостях П, Прег, Ппр и Пмакс лежит на оси светового пучка.
На фиг. 2 представлено зарегистрированное полутоновое изображение поперечного сечения пучка в плоскости Ппр, Lпр=-26 мм.
На фиг. 3 представлено в виде полутонового изображения распределение интенсивности I(х,у) по поперечному сечению пучка, приведенное к координатам в плоскости П путем замены координат в зарегистрированном распределении Iрег(ξ,η) по формулам ξ=х⋅(Lрег/Lмакс) и η=у⋅(Lрег/Lмакс), где Lрег=-34 мм и Lмакс=-997 мм.
На фиг. 4 представлено в виде полутонового изображения распределение значений волнистых деформаций волнового фронта w(x,y) по сечению пучка в плоскости П, полученное в результате применения операций способа из распределения интенсивности I(х,у), приведенного на фиг. 3.
На фиг. 5А показано распределение значений функции ψрасч(х,у) в плоскости П, полученное в результате математического моделирования, при котором распределение ψрасч(х,у) рассчитывалось с использованием уравнения (1), исходя из заданного распределения значений волнистых деформаций волнового фронта w(x,y), представленного на фиг. 4; на фиг. 5Б показано распределение значений функции ψ(х,у)=1n[I(х,у)/I(х,у)сгл] в плоскости П, вычисленное по распределению интенсивности I(х,у), представленному на фиг. 3.
Заявленный способ был экспериментально осуществлен для измерения волнистых деформаций волнового фронта, внесенных внеосевым параболическим зеркалом в световой пучок при отражении от поверхности зеркала. При изготовлении параболического зеркала его поверхность обрабатывалась малоразмерным полировочным инструментом для получения заданного асферического (параболического) профиля.
Измерения волнистых деформаций проводились на созданной экспериментальной установке, оптическая схема которой представлена на фиг. 1.
В фокальном узле коллиматора 5 излучение от лампы накаливания 1 проецируется конденсором 2 на отверстие микродиафрагмы 4 диаметром 100 мкм через узкополосный светофильтр 3 с максимумом пропускания на длине волны 0,67 мкм. Зеркало коллиматора 5 с фокусным расстоянием 7000 мм формирует на выходе коллиматора плоскопараллельный пучок с однородным распределением интенсивности. Сформированный пучок диаметром 160 мм направляют на установленное в рабочем положении внеосевое параболическое зеркало 6 с фокусным расстоянием 1000 мм, вносящее искажения в волновой фронт отраженного от зеркала сферически сходящегося пучка. ПЗС-матрицу 7 автоколлимационным методом выставляют ортогонально оси отраженного от зеркала 6 пучка в области фокусировки излучения.
Затем определяют местоположение плоскости Пмакс на оси отраженного от зеркала пучка путем перемещения ПЗС-матрицы вдоль каустики светового пучка, сравнения пиковых значений интенсивности в разных позициях по ходу пучка при помощи стандартных программных средств из комплекта технического обеспечения цифровой ПЗС-матрицы, и фиксации положения ПЗС-матрицы, в котором пиковая интенсивность излучения имеет наибольшее значение Iмакс. В найденном положении, т.е. в плоскости Пмакс, ПЗС-матрицу, в случае необходимости, дополнительно центрируют относительно пучка. Используя систему отсчета, задаваемую системой координат в плоскости Пмакс, в которой начало координат лежит на оси светового пучка, а положительное направление оси аппликат совпадает с направлением распространения светового пучка, измеряют расстояние Lмакс от плоскости Пмакс до плоскости П. В нашем эксперименте Lмакс=-997 мм.
Определяют положение плоскости Ппр, выбирая расположение этой плоскости на расстоянии |Lпр|=103⋅λ⋅(Lмакс/D)2 от плоскости Пмакс против хода пучка, регистрируют в ней распределение интенсивности светового пучка I(u,v), где u и v координаты в плоскости Ппр. В нашем эксперименте Lпр=-26 мм.
На Фиг. 2 представлено изображение поперечного сечения пучка в плоскости Ппр. Отчетливо видны квазипериодические неоднородности в распределении интенсивности пучка. Далее определяют функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл], где I(u,v)сгл - распределение интенсивности в поперечном сечении пучка, сглаженное методом наименьших квадратов. При этом функцию I(u,v)сгл аппроксимируют суммой полиномов того или иного вида. В нашем случае это был степенной полином второго порядка. При выполнении вычислений функции ψ(u,v) координаты u и v в плоскости Ппр в распределении I(u,v) заменяют на дискретные переменные по формулам ui=(i-i0)⋅h1, vj=(j-j0)⋅h1, где h1 - размер элемента изображения (пиксела ПЗС-матрицы) в плоскости Ппр, i=0,…М и j=0,…М - индексы нумерации пикселей ПЗС-матрицы, i0 и j0 индексы пиксела в центре поперечного сечения пучка, т.е. на его оси, М - число пикселей ПЗС-матрицы, укладывающихся на диаметре изображения поперечного сечения пучка в плоскости Ппр.
С учетом дискретного характера координатных данных выполняют разложение функции ψ(ui,vj) в двумерный тригонометрический ряд Фурье. Из полученного двумерного амплитудного спектра гармоник ряда Фурье находят порядковый номер μмакс=18 наивысшей из гармоник, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник.
Из соотношения |Lрег|=4⋅λ⋅(Lмакс⋅μмакс/D)2 определяют расстояние |Lрег|, отсчитываемое от плоскости Пмакс. В эксперименте было выбрано направление отсчета |Lрег| против хода пучка. Определив положение плоскости Прег, устанавливают в этом положении ПЗС-матрицу и регистрируют распределение интенсивности Iрег(ξ,η) светового пучка. Уточним здесь, что согласно правилу знаков, расстояния Lпр, Lрег и Lмакс между плоскостями Пмакс и Ппр, Прег и П, соответственно, считают положительными, если отсчет ведется от плоскости Пмакс по ходу пучка, и отрицательными при отсчете в обратном направлении. В нашем эксперименте Lрег=-34 мм. Измерение расстояний Lпр, Lрег и Lмакс осуществляют общеизвестными измерительными средствами.
На фиг. 3 представлено в виде полутонового изображения распределение интенсивности I(х,у) по поперечному сечению пучка, приведенное к координатам в плоскости П путем замены координат в распределении Iрег(ξ,η) по формулам ξ=х⋅(Lрег/Lмакс) и η=у⋅(Lрег/Lмакс). Далее определяют функцию ψ(х,у)=ln[I(х,у)/I(х,у)сгл], где I(х,у)сгл - распределение интенсивности в поперечном сечении пучка, сглаженное методом наименьших квадратов. При выполнении операции сглаживания функция I(х,у)сгл была аппроксимирована двумерным степенным полиномом второго порядка.
При выполнении вычислений функции ψ(х,у) координаты х и у в плоскости П заменяют на дискретные переменные по формулам xk=(k-k0)⋅h, yn=(n-n0)⋅h, где h=h1⋅|Lмакс/Lрег|, a h1 - размер элемента изображения (пиксела ПЗС-матрицы) в плоскости Прег, здесь k=0,…N и n=0,…N - индексы нумерации пикселей ПЗС-матрицы, по и ко индексы пиксела в центре поперечного сечения пучка, т.е. на его оси, N - наибольшее целое число, не превышающее величину (D/h), где D - диаметр пучка в плоскости П. Величина h определяет размер дискретного элемента изображения в плоскости П.
При вычислении волнистых деформаций волнового фронта функцию w(x,y) ищут в виде двумерного тригонометрического полинома, который с учетом дискретного характера координатных данных имеет вид:
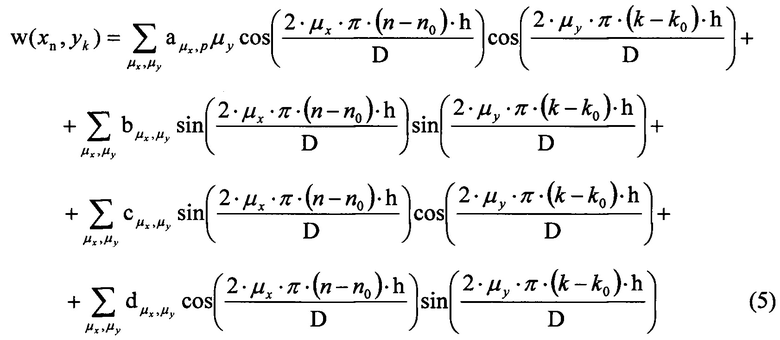
Значения коэффициентов тригонометрического полинома определяют по формулам (3), заменяя операцию интегрирования суммированием по индексам, а функцию ƒ(x,y) на ƒ[h(n-n0),h(k-k0)]=[Lрег/Lмакс⋅(Lмакс-Lрег)]⋅ψ[h(n-n0),h(k-k0)]. Область интегрирования 2 при переходе к дискретным координатам преобразуется в двумерный массив индексов k и n дискретных элементов, составляющих изображение поперечного сечения пучка.
Вычислив коэффициенты полинома, получают распределение значений волнистых деформаций волнового фронта w(xn,yk) по поперечному сечению пучка. В числовом виде значения w(xn,yk) образуют трехмерный массив числовых данных. На его основе было выполнено представление распределения деформаций волнового фронта в виде полутонового изображения, в котором яркость дискретного элемента изображения отвечает величине деформации волнового фронта в данной точке изображения пучка. Поскольку и в этом изображении, и в рассматриваемых нами далее полутоновых изображениях, представляющих распределение значений функции ψ(хn,уk), характерный линейный масштаб изменений яркости, как правило, в десятки раз превышает размер дискретного элемента изображения, то при дальнейшем анализе полученных данных можно пренебречь дискретностью координат и рассматривать полученные распределения как непрерывные функции координат х и у. Полутоновое изображение распределения волнистых деформаций волнового фронта w(x,y) по поперечному сечению пучка представлено на фиг. 4. На фиг. 4 отчетливо видна модуляция яркости изображения, демонстрирующая волнистые деформации волнового фронта.
На основании полученных данных было рассчитано среднеквадратичное значение волнистых деформаций волнового фронта, которое составило величину σw=2.4 нм, что в долях длины волны света дает σw≈λ/280. Полученное значение подтверждает на практике возможность определения предложенным способом волнистых деформаций волнового фронта на уровне значений в единицы нанометров по всему поперечному сечению пучка.
Проверка правильности решения уравнения (1) выбранным численным методом была выполнена следующим образом. Вычисляют левую часть уравнения (1), т.е. 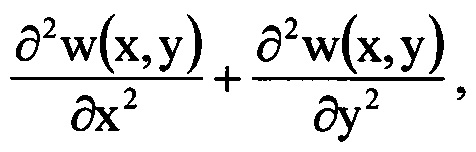 подставляя в нее двумерный тригонометрический полином вида (5), представляющий собой найденное распределение w(x,y). Приравнивая полученный результат к правой части уравнения (1), расчетным образом определяют распределение значений функции
подставляя в нее двумерный тригонометрический полином вида (5), представляющий собой найденное распределение w(x,y). Приравнивая полученный результат к правой части уравнения (1), расчетным образом определяют распределение значений функции 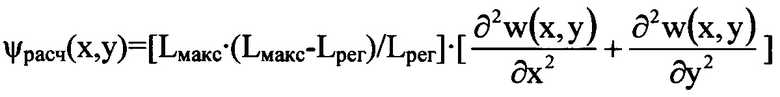 в плоскости П.
в плоскости П.
На фиг. 5А показано полутоновое изображение полученной таким образом функции ψрасч(х,у). На фиг. 5Б представлено полутоновое изображение функции ψ(x,y)=ln[I(x,y)/I(x,y)сгл] в плоскости П, полученное на основе экспериментальных данных из распределения интенсивности I(х,у), представленного на фиг. 3. Сравнение этих изображений показывает хорошее сходство картин вплоть до деталей распределения неоднородностей интенсивности.
Таким образом, конкретный пример применения способа для определения волнистых деформаций волнового фронта параболического зеркала и результаты математического моделирования предложенного способа подтверждают его основные достоинства: простоту реализации, высокую точность получаемых результатов и снижение трудоемкости процесса измерений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680657C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2753627C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕЛКОМАСШТАБНЫХ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА | 2024 |
|
RU2830845C1 |
| СПОСОБ АНАЛИЗА ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПОЛЯ | 2010 |
|
RU2430389C1 |
| УСТРОЙСТВО БЕСКОНТАКТНОГО КОНТРОЛЯ УГЛОВ ЗАТОЧКИ И КООРДИНАТ ВЕРШИНЫ ИНСТРУМЕНТА НА СТАНКАХ С ЧИСЛОВЫМ ПРОГРАММНЫМ УПРАВЛЕНИЕМ (ЧПУ) | 2009 |
|
RU2399461C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ПУЧКА МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ | 1990 |
|
RU2034322C1 |
| СПОСОБ АНАЛИЗА ВОЛНОВЫХ ФРОНТОВ СВЕТОВОГО ПОЛЯ | 1992 |
|
RU2051397C1 |
| УСТРОЙСТВО ДЛЯ ТЕРМОЗАКАЛКИ РЕЖУЩЕЙ КРОМКИ РЕЗЦА | 2007 |
|
RU2341568C2 |
| Способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице | 2023 |
|
RU2821162C1 |
| Система формирования широкополосного гиперспектрального изображения на основе сжатого зондирования с нерегулярной дифракционной решеткой | 2014 |
|
RU2653772C1 |



Изобретение относится к области оптики и может быть использовано для определения деформаций волнового фронта светового пучка, прошедшего оптическую систему, вызванных волнистостью поверхностей оптической системы. В заявленном способе направляют некогерентный гомоцентрический световой пучок с длиной волны λ на оптическую систему. Определяют положение плоскости Пмакс, в которой пиковая интенсивность светового пучка в изображении поперечного сечения светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка. Измеряют диаметр D светового пучка в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, и расстояние Lмакс до нее от плоскости Пмакс. Регистрируют распределение интенсивности I(u,v) светового пучка в координатах (u,v) плоскости Ппр, определяют и разлагают функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл] в двумерный тригонометрический ряд Фурье, находят порядковый номер μмакс наивысшей из гармоник ряда Фурье, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник. Регистрируют распределение интенсивности Iрег(ξ,η) светового пучка в координатах плоскости Прег, при этом положения плоскостей Ппр и Прег выбирают на удалении от плоскости Пмакс согласно введенным соотношениям, учитывающим значения λ, D, μмакс, Lмакс. Деформации волнового фронта светового пучка w(x,y), вызванные волнистостью поверхностей оптической системы, определяют из уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег, при этом используют распределение интенсивности светового пучка I(х,у), выраженное в координатах плоскости П путем замены переменных в распределении Iрег(ξ,η):
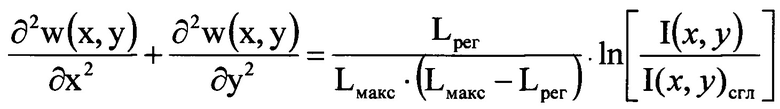 .
.
Уравнение решают вариационным методом при свободных граничных условиях, аппроксимируя w(x,y) тригонометрическим полиномом. Технический результат - определение деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, с высокой точностью при существенном упрощении процесса измерений и уменьшении его трудоемкости. 5 ил.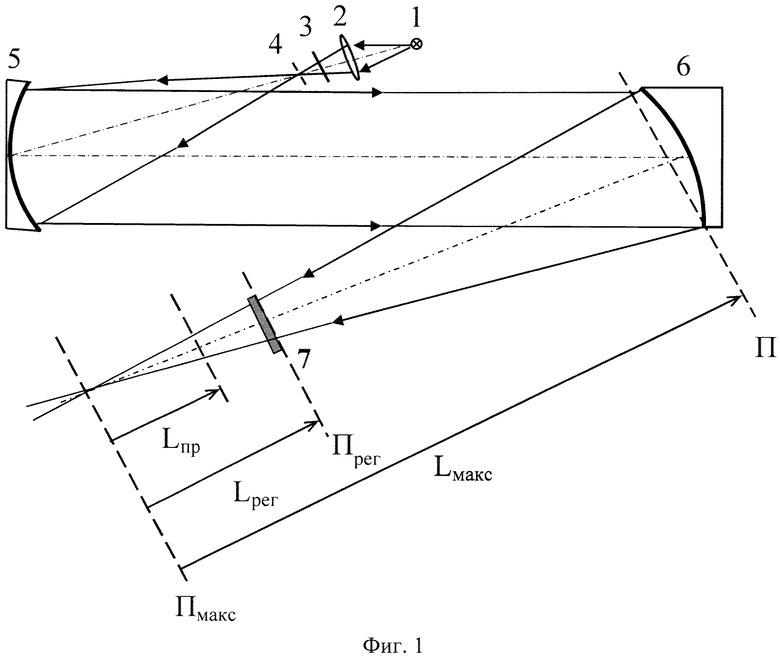
Способ определения деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, включающий направление гомоцентрического светового пучка с длиной волны λ на оптическую систему, получение математического выражения для определения деформаций волнового фронта светового пучка, определение деформаций волнового фронта светового пучка путем решения численным методом полученного математического выражения, отличающийся тем, что световой пучок, направляемый на оптическую систему, формируют некогерентным, определяют положение плоскости Пмакс, перпендикулярной оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, в которой пиковая интенсивность светового пучка в изображении поперечного сечения светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измеряют диаметр D светового пучка в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, измеряют расстояние Lмакс по оси пучка от плоскости Пмакс до плоскости П с учетом правила знаков, регистрируют распределение интенсивности I(u,v) светового пучка в координатах (u,v) плоскости Ппр, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие 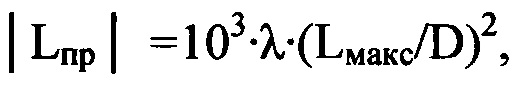 где Lпр - расстояние по оси пучка от плоскости Пмакс до плоскости Ппр с учетом правила знаков, определяют функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл], где I(u,v)сгл - распределение интенсивности I(u,v), сглаженное с использованием метода наименьших квадратов, выполняя разложение функции ψ(u,v) в двумерный тригонометрический ряд Фурье, получают двумерный амплитудный спектр гармоник ряда Фурье, находят порядковый номер μмакс наивысшей из гармоник ряда Фурье, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник, регистрируют распределение интенсивности Iрег(ξ,η) светового пучка в координатах (ξ,η) плоскости Прег, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие
где Lпр - расстояние по оси пучка от плоскости Пмакс до плоскости Ппр с учетом правила знаков, определяют функцию ψ(u,v)=ln[I(u,v)/I(u,v)сгл], где I(u,v)сгл - распределение интенсивности I(u,v), сглаженное с использованием метода наименьших квадратов, выполняя разложение функции ψ(u,v) в двумерный тригонометрический ряд Фурье, получают двумерный амплитудный спектр гармоник ряда Фурье, находят порядковый номер μмакс наивысшей из гармоник ряда Фурье, квадрат амплитуды которой составляет не менее 0,02 от квадрата максимального значения амплитуды в спектре гармоник, регистрируют распределение интенсивности Iрег(ξ,η) светового пучка в координатах (ξ,η) плоскости Прег, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие 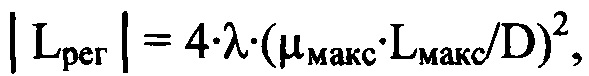 где Lрег - расстояние по оси пучка от плоскости Пмакс до плоскости Прег с учетом правила знаков, при этом начало координат в плоскостях П, Прег, Ппр лежит на оси светового пучка, математическое выражение для определения деформаций волнового фронта светового пучка w(x,y), вызванных волнистостью поверхностей оптической системы, определяют в виде уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
где Lрег - расстояние по оси пучка от плоскости Пмакс до плоскости Прег с учетом правила знаков, при этом начало координат в плоскостях П, Прег, Ппр лежит на оси светового пучка, математическое выражение для определения деформаций волнового фронта светового пучка w(x,y), вызванных волнистостью поверхностей оптической системы, определяют в виде уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
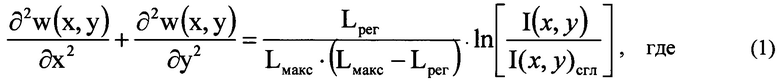
- I(x,y) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности Iрег(ξ,η) по формулам ξ=x⋅(Lрег/Lмакс) и η=y⋅(Lрег/Lмакс);
- I(х,у)сгл - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка I(х,у);
значения w(x,y) определяют путем численного решения уравнения (1) вариационным методом при свободных граничных условиях, аппроксимируя w(x,y) тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник μx и μy, пробегающими диапазон от 1 до μмакс, за исключением тех членов ряда, для которых оба порядковых номера μx и μy имеют значения, меньшие 10.
| Н.В | |||
| Барышников, Я.В | |||
| Гладышева, Д.Г | |||
| Денисов, И.В | |||
| Животовский, В.Е | |||
| Патрикеев, И.Н | |||
| Судариков | |||
| Вестник МГТУ им | |||
| Н.Э | |||
| Баумана | |||
| Сер | |||
| "Приборостроение", 2012, с | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| RU 2010125275 A, 06.11.2008 | |||
| Способ контроля оптических асферических поверхностей вращения второго порядка | 1988 |
|
SU1649260A1 |
| US 6496253 B1, 17.12.2002. | |||
Авторы
Даты
2019-02-25—Публикация
2018-04-10—Подача