Изобретение относится к физическим системам в аспекте новых методов определения плотности неизлучающих из-за запрета по спину, некогерентных частиц, таких как темных экситонов, в полупроводниковых системах экситонных поляритонов, недоступных для определения оптическими методами. Может применяться для исследования нерезонансно возбуждаемых поляритонных бозе-конденсатов и квантовых жидкостей выше порога конденсации, как при импульсном, так и при постоянном оптическом возбуждении.
В качестве уровня техники, поясняющего сущность изобретения, предлагаются к рассмотрению микрорезонаторы, такие как плоские оптические резонаторы Фабри-Перо, микропроволоки и микроколонны на базе органических и неорганических полупроводников, заполненных активной средой, поддерживающей экситонные состояния, возбуждаемые нерезонансно при помощи импульсной или постоянной лазерной накачки выше порога бозе-эйнштейновской конденсации (J. Kasprzak,M. Richard, S. Kundermann, A. Baas, P. Jeambrun, J. M. J. Keeling, F. M. Marchetti, M. H. Szymánska, R. André, J. L. Staehli, V. Savona, P. B. Littlewood, B. Deveaud, and Le Si Dang, Bose-Einstein condensation of exciton polaritons, Nature (London) 443, 409-414 (2006)). Из-за способа накачки в таких системах равновероятно образуются экситонные состояния с различными значениями суммарного спина, только часть из которых, отвечающая спиновым ветвям J = ±1, может излучать и превращаться в экситонные поляритоны. Экситоны с J = ±2 не могут радиационно рекомбинировать и потому не могут быть детектированы оптическими методами (J.-M. Ménard, C. Poellmann, M. Porer, U. Leierseder, E. Galopin, A. Lemaître, A. Amo, J. Bloch and R. Huber, Revealing the dark side of a bright exciton-polariton condensate, Nat. Commun. 5, 4648 (2014)).
Способ измерения плотности темных экситонов базируется на влиянии взаимодействия оптически активных поляритонов с оптически недетектируемыми темными экситонами за счет кулоновского взаимодействия с зависимостью от импульса. Рассматривается экситон-поляритонная система с экситон-экситонным взаимодействием в состоянии динамического либо термодинамического равновесия, находящаяся при конечной температуре. Особенность данной системы заключается в том, что закон дисперсии бозе-конденсирующихся частиц (экситонных поляритонов) является сильно непараболичным вдали от области нулевых импульсов, бозе-конденсация происходит в присутствии некогерентного резервуара, причем взаимопревращение темных экситонов в светлые отсутствует, а взаимодействие поляритонов друг с другом и с темными экситонами зависит от импульсов. Такая система может быть описана в рамках приближения Хартри-Фока-Боголюбова-Попова в предположении термодинамического равновесия, если скорость релаксации системы много меньше утечки фотонов из резонатора. В работе (A. M. Grudinina, I. L. Kurbakov, Yu. E. Lozovik, and N. S. Voronova, Finite-temperature Hartree-Fock-Bogoliubov theory for exciton-polaritons, Phys. Rev. B 104, 125301 (2021)) показано, что учет ненулевой температуры и темных экситонов в системе дает поправки к выражениям для химического потенциала, боголюбовских спектров возбуждения и, в том числе, скорости звука в поляритонной квантовой жидкости. Данная «боголюбовская» скорость звука в рамках данного рассмотрения определяется значительно более сложным выражением по сравнению с полученными ранее зависимостями скорости звука от химического потенциала, и, в общем случае, не является пропорциональным корню из химического потенциала и, в том числе, определяется плотностью темных некогерентных «фоновых» частиц, которая в работе (A. M. Grudinina, I. L. Kurbakov, Yu. E. Lozovik, and N. S. Voronova, Finite-temperature Hartree-Fock-Bogoliubov theory for exciton-polaritons, Phys. Rev. B 104, 125301 (2021)) является входным неопределяемым параметром.
Предложенный способ не имеет аналогов и базируется на методе картирования зависимости экспериментально измеренной скорости звука в поляритонных квантовых жидкостях от химического потенциала (экспериментально измеряемого голубого смещения линии фотолюминесценции поляритонного бозе-конденсата) при изменении параметров некогерентной лазерной накачки.
Технический результат заключается в возможности бесконтактного получения информации о плотности темных (неизлучающих) экситонов в полупроводниковых системах экситонных поляритонов, недоступной для измерения оптическими методами.
Технический результат достигается тем, что определяется плотность неизлучающего и некогерентного экситонного резервуара по независимо экспериментально измеряемым голубому смещению линии фотолюминесценции поляритоного бозе-конденсата и углу наклона закона дисперсии элементарных возбуждений этого конденсата, при этом экситон-поляритонная система возбуждается нерезонансно постоянной или импульсной лазерной накачкой, при этом производится картирование зависимости скорости звука в поляритонной жидкости, определяемой углом наклона закона дисперсии, от голубого смещения линии фотолюминесценции при заданных экспериментальных параметрах системы.
Поляритонные бозе-конденсаты регулярно достигаются при повышенных температурах (от 4 K до комнатной) в неравновесных реализациях. Как правило, возбуждающий лазер настраивается либо в резонансе с нижней поляритонной ветвью (LPB), либо сильно выше экситонной дисперсии, что приводит к образованию так называемого резервуара, который релаксирует в сторону поляритонных LPB-состояний и в конечном итоге переходит в основное состояние. Последний способ реализации поляритонных конденсатов поясняется на фиг. 1. Из-за конечного времени жизни популяция поляритонов либо распадается во времени после импульса возбуждения, либо должна постоянно пополняться за счет непрерывной накачки. Такая управляемая-диссипативная природа системы приводит к модификации спектра элементарных возбуждений, нарушению галилеевской инвариантности и критерия Ландау, что крайне важно для понимания и описания специфики поляритонной сверхтекучести. Темные, или запрещенные к излучательной рекомбинации по спину (J = ±2, где J обозначает проекцию суммарного спина экситона), экситоны создаются в системе при нерезонансном возбуждении вместе со светлыми, излучающими (J = ±1) экситонными популяциями (в целом, существует четыре экситонных ветви на каждую квантовую яму, которые заселяются в процессе релаксации носителей заряда). Современные исследования показывают, что такой темный резервуар может быть высоконаселенным (J.-M. Ménard, C. Poellmann, M. Porer, U. Leierseder, E. Galopin, A. Lemaître, A. Amo, J. Bloch and R. Huber, Revealing the dark side of a bright exciton-polariton condensate, Nat. Commun. 5, 4648 (2014)) и долгоживущим (D. Schmidt, B. Berger, M. Kahlert, M. Bayer, C. Schneider, S. Höfling, E. S. Sedov, A. V. Kavokin, and M. Aßmann, Tracking Dark Excitons with Exciton Polaritons in Semiconductor Microcavities, Phys. Rev. Lett. 122, 047403 (2019)). Плотность темного экситонного резервуара невозможно определить оптическими методами из-за запрета излучательной рекомбинации. Предложенный способ описывает динамику такой сложносоставной системы и основывается на аналитически решаемой системе дифференциальных уравнений, связывающей плотность неактивного резервуара (горячей электрон-дырочной плазмы, создаваемой в полупроводнике лазером накачки) nin, плотность темного резервуара nD и полную плотность поляритонной системы n:
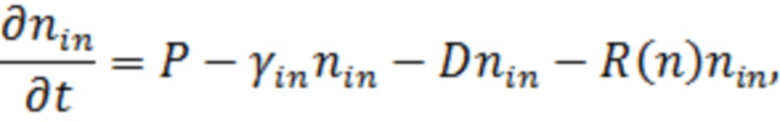
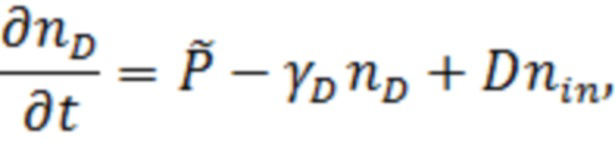
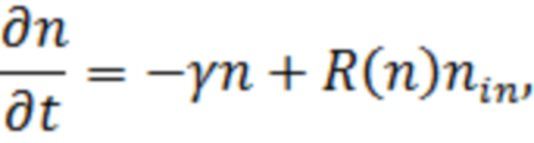
где γin, γD и γ – скорости утечки из трех подсистем, а D и R(n) описывают скорости перехода частиц из неактивного резервуара в темный и в поляритонную подсистему, соответственно. Накачка входит в уравнения для nin и nD как P и 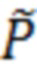 . Все коэффициенты в данной системе уравнений могут быть определены из прямого сравнения с экспериментом при наблюдении за динамикой фотолюминесценции из поляритонного конденсата. Основное отличие данной модели от ранее разработанных подходов заключается в том, что она описывает динамическое наполнение системы экситонных поляритонов с полной плотностью n, после чего уравновешивание между бозе-конденсатом с плотностью n0 и неконденсированными частицами (надконденсатом) с плотностью n’ предполагается регулируемым термодинамически, при заданной температуре системы. Данная система уравнений описывает одновременно как случай импульсной накачки (при котором необходимо положить P =
. Все коэффициенты в данной системе уравнений могут быть определены из прямого сравнения с экспериментом при наблюдении за динамикой фотолюминесценции из поляритонного конденсата. Основное отличие данной модели от ранее разработанных подходов заключается в том, что она описывает динамическое наполнение системы экситонных поляритонов с полной плотностью n, после чего уравновешивание между бозе-конденсатом с плотностью n0 и неконденсированными частицами (надконденсатом) с плотностью n’ предполагается регулируемым термодинамически, при заданной температуре системы. Данная система уравнений описывает одновременно как случай импульсной накачки (при котором необходимо положить P =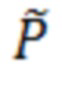 = 0 и задавать начальные плотности подсистем, а именно, входные плотности неактивного резервуара nin(0) и темных экситонов nD(0), так и случай постоянной накачки, при котором соотношение
= 0 и задавать начальные плотности подсистем, а именно, входные плотности неактивного резервуара nin(0) и темных экситонов nD(0), так и случай постоянной накачки, при котором соотношение 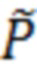 /P определяет входную плотность темных экситонов в системе). Важно отметить, что в обоих случаях простота уравнений допускает аналитическое решение и не требует численного моделирования.
/P определяет входную плотность темных экситонов в системе). Важно отметить, что в обоих случаях простота уравнений допускает аналитическое решение и не требует численного моделирования.
Используя данную модель, в каждый момент времени t можно непосредственно использовать величину nD для нахождения вклада темных экситонов в голубое смещение линии фотолюминесценции, определяемое как
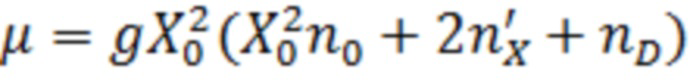 ,
,
где g – константа экситонного взаимодействия, а X0 – экситонный коэффициент Хопфилда, доступное для прямого экспериментального измерения. Для определения вкладов поляритонного конденсата n0 и светлых надконденсатных экситонов 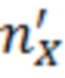 , для каждого n(t) проводится самосогласованный расчет при заданной температуре в соответствии с подходом Хартри-Фока-Боголюбова, который позволяет рассчитать боголюбовскую скорость звука. Эта процедура позволяет получить зависимость отношения конденсата к резервуару, голубое смещение и скорость звука в каждый момент времени t с полученными плотностями.
, для каждого n(t) проводится самосогласованный расчет при заданной температуре в соответствии с подходом Хартри-Фока-Боголюбова, который позволяет рассчитать боголюбовскую скорость звука. Эта процедура позволяет получить зависимость отношения конденсата к резервуару, голубое смещение и скорость звука в каждый момент времени t с полученными плотностями.
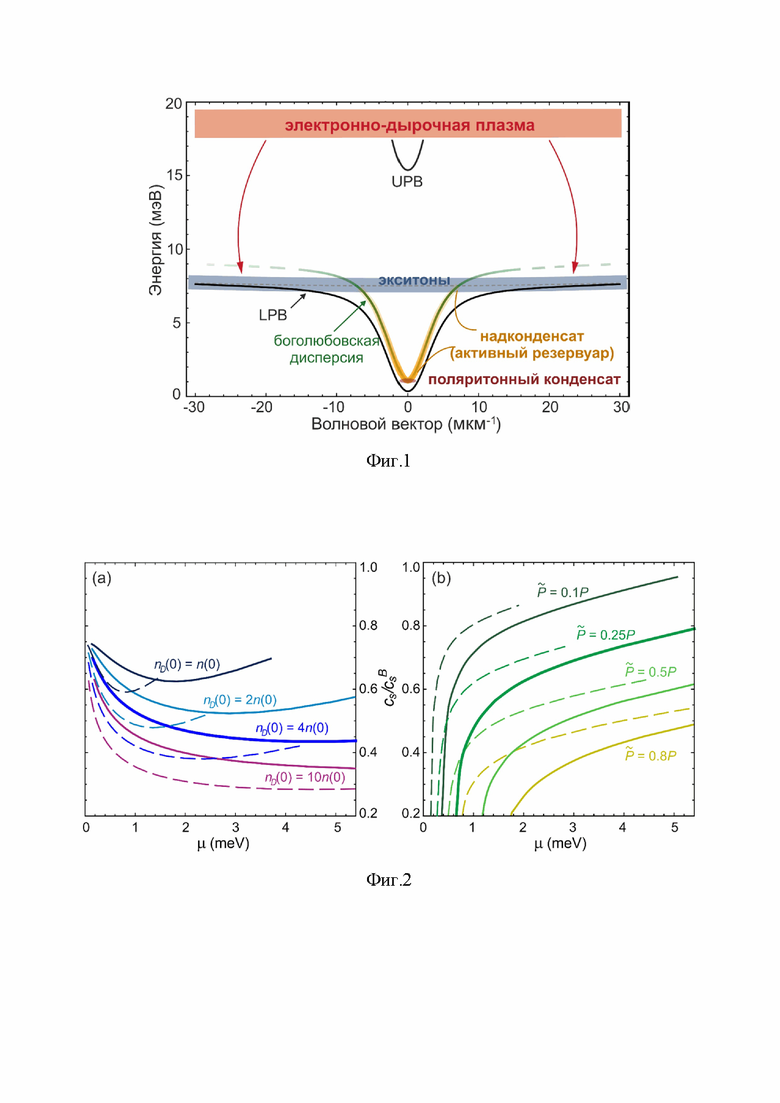
На фиг. 2 обобщается поведение отношения рассчитанной в предложенной модели скорости звука к «стандартной» боголюбовской скорости 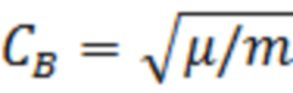 (m – эффективная масса поляритона) для обоих типов возбуждения, для варьируемых плотностей темных экситонов при фиксированной мощности накачки. Можно видеть, что экспериментально соответствующие плотности темных экситонов резко изменяют ожидаемые скорости звука поляритонов. Зависимость Cs(μ) наиболее чувствительна к соотношению между плотностями конденсата и резервуара в системе. В случае схемы импульсной накачки это соотношение меняется со временем, и зависимость Cs(μ) немонотонна, но остается в диапазоне 0.3-0.7CB для всех рассмотренных плотностей nD. Для постоянного некогерентного возбуждения чуть выше порога (т.е. при малых голубых смещениях) скорость звука очень мала, и быстро растет с мощностью накачки P до значений 0.5-0.85CB по мере увеличения доли конденсата. Таким образом, на рисунке 2 показаны семейства кривых, отображающих зависимости Cs(μ) для разных плотностей темных экситонов в системе. Поскольку скорости распада и рассеяния между подсистемами в исходной системе уравнений могут быть найдены путем точного фитирования экспериментально наблюдаемой конденсатной фотолюминесценции, картирование экспериментально измеренной зависимости Cs(μ) в относительно широком диапазоне голубых смещений предлагает способ определения плотности темных экситонов в системе при заданной температуре и мощности накачки (см. A.M. Grudinina and N.S. Voronova, Dark and thermal reservoir contributions to polariton sound velocity, Physical Review B 106, L121301 (2022)).
(m – эффективная масса поляритона) для обоих типов возбуждения, для варьируемых плотностей темных экситонов при фиксированной мощности накачки. Можно видеть, что экспериментально соответствующие плотности темных экситонов резко изменяют ожидаемые скорости звука поляритонов. Зависимость Cs(μ) наиболее чувствительна к соотношению между плотностями конденсата и резервуара в системе. В случае схемы импульсной накачки это соотношение меняется со временем, и зависимость Cs(μ) немонотонна, но остается в диапазоне 0.3-0.7CB для всех рассмотренных плотностей nD. Для постоянного некогерентного возбуждения чуть выше порога (т.е. при малых голубых смещениях) скорость звука очень мала, и быстро растет с мощностью накачки P до значений 0.5-0.85CB по мере увеличения доли конденсата. Таким образом, на рисунке 2 показаны семейства кривых, отображающих зависимости Cs(μ) для разных плотностей темных экситонов в системе. Поскольку скорости распада и рассеяния между подсистемами в исходной системе уравнений могут быть найдены путем точного фитирования экспериментально наблюдаемой конденсатной фотолюминесценции, картирование экспериментально измеренной зависимости Cs(μ) в относительно широком диапазоне голубых смещений предлагает способ определения плотности темных экситонов в системе при заданной температуре и мощности накачки (см. A.M. Grudinina and N.S. Voronova, Dark and thermal reservoir contributions to polariton sound velocity, Physical Review B 106, L121301 (2022)).
Предложенная аналитически решаемая модель, основанная на самосогласованном подходе Хартри-Фока-Боголюбова и кинетических уравнениях, позволяет исследовать влияние темных экситонов и светлого, теплового поляритонного резервуара на скорость звука в нерезонансно накачиваемых поляритонных жидкостях. Входными параметрами являются скорости распада и скорости рассеяния, которые могут быть найдены из простого фитирования экспериментальных данных. Предложенный способ позволяет непосредственно вычислить голубое смещение и скорость звука как для импульсного, так и для постоянного нерезонансного возбуждения системы. Поскольку в поляритонных экспериментах голубой сдвиг и наклон дисперсии элементарных возбуждений в области малых импульсов могут быть измерены независимо, отображение (картирование) таких измерений на зависимости Cs(μ), примеры которых показаны на фиг. 2.
Таким образом, предлагаемый способ обеспечивает достижение требуемого технического результата, заключающегося в возможности бесконтактного получения информации о плотности темных (неизлучающих) экситонов в полупроводниковых системах экситонных поляритонов, недоступной для измерения другими оптическими методами.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ КУБИТА | 2018 |
|
RU2716028C1 |
| Способ оптического управления линейной поляризацией излучения | 2022 |
|
RU2801774C1 |
| УНИВЕРСАЛЬНЫЙ ПОЛНОСТЬЮ ОПТИЧЕСКИЙ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ | 2021 |
|
RU2756257C1 |
| ПРОГРАММИРУЕМЫЙ ПОЛЯРИТОННЫЙ СИМУЛЯТОР | 2020 |
|
RU2745206C1 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ МАКРОСКОПИЧЕСКОГО СОСТОЯНИЯ ПОЛЯРИТОНОВ ПРИ ПОМОЩИ ОДНОГО ФОТОНА | 2020 |
|
RU2782686C2 |
| МЕТОД ПЕРЕКЛЮЧЕНИЯ СОСТОЯНИЯ ПОЛЯРИТОННОГО КОНДЕНСАТА | 2023 |
|
RU2830391C2 |
| ПОЛЯРИТОННЫЙ ЛАЗЕР | 2015 |
|
RU2611087C1 |
| ОПТИЧЕСКИЙ ПОЛУПРОВОДНИКОВЫЙ ЭЛЕМЕНТ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ, ОПТИЧЕСКИЙ ПОЛУПРОВОДНИКОВЫЙ ЭЛЕМЕНТ НА ОСНОВЕ ОКСИДА ЭЛЕМЕНТА II ГРУППЫ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 1998 |
|
RU2169413C2 |
| СПОСОБ ОБНАРУЖЕНИЯ И ИДЕНТИФИКАЦИИ ХИМИЧЕСКИХ И БИОЛОГИЧЕСКИХ ОБЪЕКТОВ В РАСТВОРАХ ВЫСОКОГО РАЗБАВЛЕНИЯ ПО СТРУКТУРНЫМ ИЗМЕНЕНИЯМ СРЕДЫ | 2004 |
|
RU2292035C2 |
| Способ контроля квантового состояния поляритонного кубита | 2023 |
|
RU2821704C1 |
Изобретение относится к области измерений, а именно к определению плотности темных экситонов в полупроводниковых системах экситонных поляритонов. Способ определения плотности темных экситонов включает определение плотности неизлучающего и некогерентного экситонного резервуара по независимо экспериментально измеряемым голубому смещению линии фотолюминесценции поляритонного бозе-конденсата и углу наклона закона дисперсии элементарных возбуждений этого конденсата, при этом экситон-поляритонная система возбуждается нерезонансно постоянной или импульсной лазерной накачкой, при этом производится картирование зависимости скорости звука в поляритонной жидкости, определяемой углом наклона закона дисперсии, от голубого смещения линии фотолюминесценции при заданных экспериментальных параметрах системы. Технический результат - бесконтактное получение информации о плотности темных (неизлучающих) экситонов в полупроводниковых системах экситонных поляритонов. 2 ил.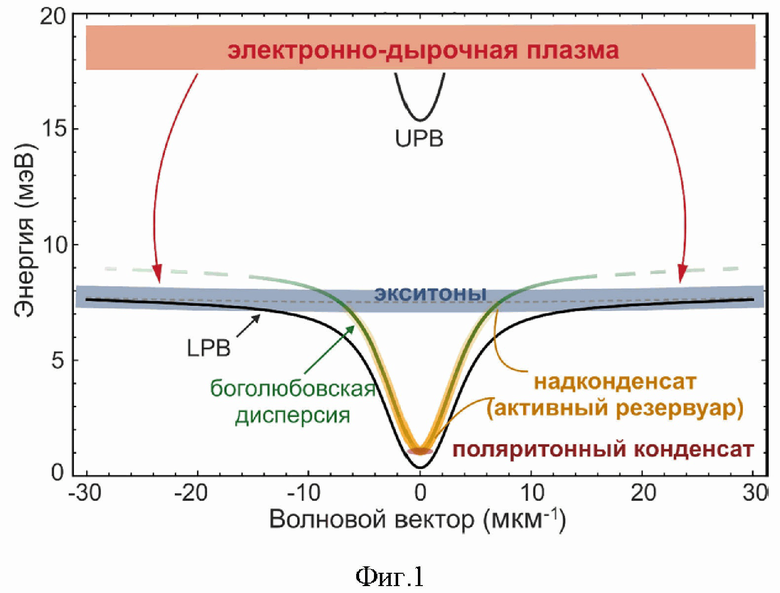
Способ измерения плотности темных экситонов в полупроводниковых системах экситонных поляритонов заключается в определении плотности неизлучающего и некогерентного экситонного резервуара по независимо экспериментально измеряемым голубому смещению линии фотолюминесценции поляритонного бозе-конденсата и углу наклона закона дисперсии элементарных возбуждений этого конденсата, при этом экситон-поляритонная система возбуждается нерезонансно постоянной или импульсной лазерной накачкой, при этом производится картирование зависимости скорости звука в поляритонной жидкости, определяемой углом наклона закона дисперсии, от голубого смещения линии фотолюминесценции при заданных экспериментальных параметрах системы.
| US 2020395448 A1, 17.12.2020 | |||
| СПОСОБ ЭФФЕКТИВНОГО ОСУЩЕСТВЛЕНИЯ ГИПЕРПРОВОДИМОСТИ И СВЕРХТЕПЛОПРОВОДНОСТИ | 2016 |
|
RU2626195C1 |
| US 2018261719 A1, 13.09.2018 | |||
| US 2018265779 A1 20.09.2018. | |||
Авторы
Даты
2024-04-03—Публикация
2023-03-02—Подача