Изобретение относится к компьютерным системам, в частности к квантовым компьютерам и оптическим логическим элементам для манипулирования данными, и может быть использовано в квантово-механических явлениях, таких как суперпозиция (в которой квантовая переменная может одновременно существовать в нескольких различных состояниях) и запутывание (в котором множественные квантовые переменные имеют связанные состояния независимо от расстояния между ними в пространстве или времени), не имеют аналогов в мир классических вычислений, и, следовательно, не может быть реализован с помощью классических вычислительных устройств.
Известна полезная модель флаксонный кольцевой детектор (Полезная модель №177295, МПК H01L 39/22). Полезная модель относится к криогенной электронике и может быть использована в измерительной технике, радиотехнических и информационных системах (в том числе и квантовых) для измерения слабых магнитных потоков (менее 0,1 кванта магнитного потока) при относительно слабом обратном влиянии на объект исследования. Более конкретно, предложен флаксонный кольцевой детектор, включающий два источника постоянного тока для системы задания рабочей точки, два генератора флаксонов, две системы детектирования микроволнового излучения, две джозефсоновские передающие линии в виде кольцевых контактов, соединенные сверхпроводящей перемычкой, связанной магнитным образом с объектом исследования. Полезная модель обеспечивает возможность определения и абсолютной величины, и направления эффективного магнитного момента исследуемой квантовой системы и дополнительно обеспечивает уменьшение обратного влияния детектора на объект исследований, что особенно важно для применения в устройствах обработки квантовой информации.
Недостатком является то, что необходимо постоянно поддержание эффективного магнитного момента для сохранения связанности двух систем.
Известен флаксонный баллистический детектор (Патент №2592735, МПК H01L 39/22), включающий генератор одноквантовых импульсов, приемник одноквантовых импульсов со схемой сравнения, две джозефсоновские передающие линии, соединяющие генератор и приемник, соединенные сверхпроводящей перемычкой, связанной магнитным образом с объектом исследования. Технический результат: обеспечение возможности реализации измерения сверхслабых сигналов.
Недостатком является то, что такая система измерения вносит существенное искажения в значение измеряемой величины.
Известен Способ определения состояния кубита (Патент 2538296, МПК G06N 99/00, G06E 3/00). Способ, основанный на считывании кубита в нескольких различных измерительных базисах, включающий воздействие на кубит электромагнитным излучением на переходах между уровнями кубита и некоторым вспомогательным уровнем. Для считывания кубита в требуемом измерительном базисе на кубит воздействуют бихроматическим излучением, спектральные компоненты которого резонансны переходам с уровней кубита на вспомогательный уровень, интенсивности и фазы спектральных компонент бихроматического излучения задают так, чтобы выделить требуемый для считывания кубита измерительный базис. Результат считывания определяют, регистрируя возбуждение кубита на вспомогательный уровень.
Недостатком является то, что для считывания в заданном базисе необходимо использовать бихроматическое излучение с жестко заданным спектральным составом.
Известен Способ Фасонные кубиты джозефсоновских контактов (Патент US 6627915, МПК G06N 99/00; H01L 39/22), в котором представлен сверхпроводящий кубит. Кубит имеет форму длинного джозефсоновского перехода с магнитным флюксоном, так что при наличии внешнего магнитного поля создается функция потенциальной энергии флюсона, указывающая множество точек пиннинга в кубите. В одном варианте осуществления формируется джозефсоновский переход в форме сердца, где захваченный флюксон имеет функцию потенциальной энергии с двойной сваркой, указывающую два места закрепления, когда переход помещается в магнитное поле, приложенное извне. Кубитом управляют путем подготовки начального состояния, создания суперпозиции двух состояний путем уменьшения магнитного поля, развития квантового состояния со временем, замораживания в конечном состоянии за счет увеличения магнитного поля и считывания конечного состояния.
Недостатком является то, что считывание кубита возможно только на основе задания начального состояния определяемого структурой магнитного поля.
Известен способ резонансная контролируемая кубитная система (Патент US US 20050101489, МПК H01L 39/22, G06F 7/48, G06N 99/00), которая характеризуется резонансной частотой. Резонансная частота системы управления является функцией тока смещения. Схема дополнительно включает в себя сверхпроводящий механизм, имеющий емкость или индуктивность. Сверхпроводящий механизм когерентно связывает сверхпроводящий кубит с резонансной системой управления. Метод перепутывания квантового состояния первого кубита с квантовым состоянием второго кубита. В способе используется резонансная система управления, которая емкостно связана с первым и вторым кубитом, настроен на первую частоту, которая соответствует разности энергий между двумя низшими уровнями потенциальной энергии первого кубита. Затем резонансная система управления настраивается на вторую частоту, соответствующую разности энергий между двумя низшими уровнями потенциальной энергии второго кубита.
Недостатком является то, что в данной системе реализована емкостная связь, ограничивающая время переключения между состояниями.
Известен Квантовый компьютерный аппарат (Патент US 7466725, МДК H01S 3/00). Квантовый компьютер включает в себя оптический резонатор, включающий группы систем, содержащие системы, каждая из которых имеет энергетические состояния с наивысшей энергией 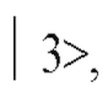 и два других энергетических состояния
и два других энергетических состояния 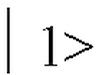 и
и 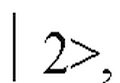 четвертое или более состояний
четвертое или более состояний 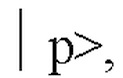 угловая частота перехода (ωij) между
угловая частота перехода (ωij) между 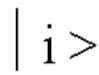 и
и 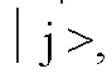 однородное уширение (Δωhomo, ij) на угловой частоте перехода между
однородное уширение (Δωhomo, ij) на угловой частоте перехода между 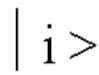 и
и 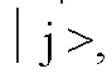 оптический резонатор, имеющий режимы резонатора, ωck k-го режима резонатора и излучающий блок, выполненный с возможностью излучать светового пучка на группу системы, и где
оптический резонатор, имеющий режимы резонатора, ωck k-го режима резонатора и излучающий блок, выполненный с возможностью излучать светового пучка на группу системы, и где 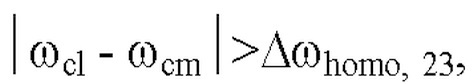 группа системы включает в себя системные подгруппы Aq, имеющие соответствующие ω23 которые резонируют с соответствующими ωcq мод резонатора, и излучающий блок выполнен с возможностью подачи светового луча двух длин волн и другого светового луча к s (1)-ому квантовому биту A qs(1)(s (l) 1~r), сформированному из r систем, выбранных из каждого Aq, луч света двух длин волн, одновременно вызывающий двухфотонный резонанс на Aq при ω12 или ω1p, другой луч света, одновременно вызывающий однофотонный резонанс на Aq при ω13 или ωр3.
группа системы включает в себя системные подгруппы Aq, имеющие соответствующие ω23 которые резонируют с соответствующими ωcq мод резонатора, и излучающий блок выполнен с возможностью подачи светового луча двух длин волн и другого светового луча к s (1)-ому квантовому биту A qs(1)(s (l) 1~r), сформированному из r систем, выбранных из каждого Aq, луч света двух длин волн, одновременно вызывающий двухфотонный резонанс на Aq при ω12 или ω1p, другой луч света, одновременно вызывающий однофотонный резонанс на Aq при ω13 или ωр3.
Недостатком является то, что для переключения состояний используется явление однородного уширения сигнала в многоуровневой квантово-механической системе.
Известен способ, контролирующий точные линии биасов в кубитовых устройствах (Патент WO/2018/182571, МДК G06N 99/00). Варианты осуществления настоящего изобретения предоставляют новые конфигурации линий смещения потока для управления сверхпроводящими квантовыми частотами битов. Пример предлагаемой структуры линии поляризации потока содержит одну центральную линию проводника, образующую две частичные петли. Другая примерная структура содержит две центральные проводящие линии, приводимые в движение отдельно, каждая из двух центральных проводящих линий образует соответствующую частичную петлю. Другая примерная структура линии поляризации потока содержит одну центральную проводящую линию, разделенную на две центральные проводящие линии, каждая из двух центральных проводящих линий образует соответствующую частичную петлю и содержит петлю с соответствующей индукцией. Такие структуры обеспечивают улучшения по сравнению с обычными линиями поляризации потока при генерации магнитного поля, которое может настраивать частоту квантового бита с достаточной степенью контроля, гарантируя, что магнитное поле не влияет существенно на другие компоненты квантовой цепи.
Недостатком является то, что в системе, состоящей из большого количества индукционных петель, возможно развитие неконтролируемого взаимодействия между ними, помимо взаимодействия с основной системой.
Известен квантовый компьютер и способ формирования множества квантовых битов (Заявка на патент 2010057743, МПК G06F 7/48, G02F 3/00). Представлен квантовый компьютер, который может установить множество квантовых битов, управляющих взаимодействием, и одновременно может контролировать отдельные квантовые биты и вводить взаимодействие между произвольными квантовыми битами по мере необходимости. Квантовый компьютер включает в себя средство для подачи лазерных лучей, средство для генерации двумерного множества лучей ближнего поля света по меньшей мере на одной плоскости из лазерных лучей, полученных от средства подачи света и квантовые биты, образованные путем захвата атомов соответственно в световых пучках ближнего поля. Квантовый компьютер включает в себя одномерную световую решетку, образованную противоположными лазерными лучами. Пара атомов, которые необходимо привести в запутанное квантовое состояние, перемещаются в одномерную световую решетку и могут взаимодействовать друг с другом.
Недостатком является то, что необходимо использовать решетку, сформированную встречными лазерными лучами, и как следствие контролировать постоянную частоту отстройки и точность позиционирования атома, ограниченную длиной волны используемого лазерного источника.
Научное состояние данного направления заключены в удивительных успехах в управлении взаимодействием света с веществом в полупроводниковых оптических микрорезонаторах, что позволило разработать новое поколение оптоэлектронных устройств. Они основаны на своеобразных свойствах экситон-поляритонов - полусветовых, полу материальных бозонных квазичастицах, возникающих из-за сильной связи между фотонной модой и экситонами в квантовых ямах, расположенных внутри резонатора, в том числе исследования бозе-эйнштейновских конденсатов экситон-поляритонов в микрорезонаторах, реализация поляритонного лазера, работающего при комнатной температуры, концепции XY-симуляторов на основе экситон-поляритонных конденсатов и наблюдение постоянных круговых токов экситон-поляритонов. Ближайший публикации по применению XY-симуляторов, основанных на сочетании экситон-поляритонных конденсатов (P.G. Lagoudakis and N.G. Berloff, "A Polariton Graph Simulator" New Journal of Physics, 19, 125008 (2017), Natalia G. Berloff, Matteo Silva, Kirill Kalinin, Alexis Askitopoulos, Julian D.  Pasquale Cilibrizzi, Wolfgang Langbein and Pavlos G. Lagoudakis "Realizing the classical XY Hamiltonian in polariton simulators," Nature Materials 16(11) 1120 (2017)) и об устойчивых круговых токов в поляритонном конденсате (V.A. Lukoshkin, V.K. Kalevich, М.М. Afanasiev, K.V. Kavokin, Z. Hatzopoulos, P.G. Savvidis, E.S. Sedov, and A.V. Kavokin, Persistent circular currents of exciton-polaritons in cylindrical pillar microcavities, Phys. Rev. В 97, 195149 (2018)). Однако, ни одна из этих работ не демонстрирует и не обсуждает двухуровневую квантовую систему, необходимую для реализации кубита. Новым изобретением является сплит-кольцевое оптическое возбуждение, приводящее к образованию такой двухуровневой системы.
Pasquale Cilibrizzi, Wolfgang Langbein and Pavlos G. Lagoudakis "Realizing the classical XY Hamiltonian in polariton simulators," Nature Materials 16(11) 1120 (2017)) и об устойчивых круговых токов в поляритонном конденсате (V.A. Lukoshkin, V.K. Kalevich, М.М. Afanasiev, K.V. Kavokin, Z. Hatzopoulos, P.G. Savvidis, E.S. Sedov, and A.V. Kavokin, Persistent circular currents of exciton-polaritons in cylindrical pillar microcavities, Phys. Rev. В 97, 195149 (2018)). Однако, ни одна из этих работ не демонстрирует и не обсуждает двухуровневую квантовую систему, необходимую для реализации кубита. Новым изобретением является сплит-кольцевое оптическое возбуждение, приводящее к образованию такой двухуровневой системы.
Техническим результатом является формирование и последующее управление квантовыми битами на основе бозе-эйнштейновских конденсатов экситон-поляритонов при непрерывной нерезонансной оптической накачке плоских полупроводниковых микрополостных структур - микрорезонаторов, в результате которой образуются конденсаты в форме незавершенного кольца, что обеспечивает закрепление темного солитона, образованного экситон-поляритонным конденсатом в щели кольца накачки.
Технический результат достигается тем, что в данном способе формирования кубита для оптической генерации тс - фазового скачка состояния за счет индуцированного резервуаром разрыва потенциала используется пучок накачки в супергауссовской форме с зазором интенсивности в центре кольца, разделяющим пятно накачки на две равные части возбуждении в плоских полупроводниковых микрорезонаторных структурах. При этом, можно управлять частотами колебаний, изменяя интенсивность накачки или ширину интервала интенсивности. В целом частота колебаний возрастает по мере ослабления потенциального барьера, что согласуется с динамикой колебаний в сверхпроводниковом джозефсоновском соединении за счет уменьшения толщины изолятора или увеличения внешнего напряжения.
Поскольку, пятно накачки имеет форму расщепленного кольца для обеспечения закрепления темного солитона, образованного экситон-поляритонным конденсатом в прорези кольца накачки, то скачок фазы поляритона на «pi» по положению темного солитона устанавливает правило отбора для квантовых состояний поляритонного конденсата в кольце. Два состояния с самой низкой энергией соответствуют круговым токам по часовой стрелке и против часовой стрелки. Две линейные комбинации этих состояний образуют базис 0 и 1 состояний кубита по полной аналогии со сверхпроводящими кубитами на основе джозефсоновских контактов.
Изобретение поясняется представленными фиг. 1-5: фиг. 1 - Профиль кольцеобразной накачки внешним радиусом WR и внутренним радиусом Wr с зазором Wg=1,5 мкм в центральной части, фиг. 2 - эволюция топологического заряда во времени для различных интенсивностей накачки Р0, фиг. 3 - профили плотности и фазы колебательного раствора в разном масштабе времени, соответствующее состоянию, показанному нижней черной точкой фиг. 2 для Р0=20., фиг. 4 - профили плотности и фазы колебательного раствора в разном масштабе времени, соответствующее состоянию, показанному верхней черной точкой фиг. 2 для Р0=20, фиг. 5 - профили плотности и фазы стационарного конденсата для Р0=30. Здесь WR=20 и Wr=6.
Заявляемый способ основан на проведенных раннее научных исследованиях, опубликованных в статьях по получению и применению XY-симуляторов, основанных на сочетании экситон-поляритонных конденсатов (P.G. Lagoudakis and N.G. Berloff, "A Polariton Graph Simulator" New Journal of Physics, 19, 125008 (2017), Natalia G. Berloff, Matteo Silva, Kirill Kalinin, Alexis Askitopoulos, Julian D. Topfer, Pasquale Cilibrizzi, Wolfgang Langbein and Pavlos G. Lagoudakis "Realizing the classical XY Hamiltonian in polariton simulators," Nature Materials 16 (11) 1120 (2017)) и об устойчивых круговых токов в поляритонном конденсате (V.A. Lukoshkin, V.K. Kalevich, М.М. Afanasiev, K.V. Kavokin, Z. Hatzopoulos, P.G. Savvidis, E.S. Sedov, and A.V. Kavokin, Persistent circular currents of exciton-polaritons in cylindrical pillar microcavities, Phys. Rev. В 97, 195149 (2018)).
Особенность способа заключается в том, что предлагаемый способ организации бита имеет квантовую природу и основан на использовании бозе-эйнштеновских конденсатов экситон-поляритонов. Преимуществом поляритона перед сверхпроводящими кубитами является более высокая рабочая температура (до комнатной температуры в широкополосных полупроводниковых микрорезонаторах). Такое решение приведет к простой интегрируемости с классическими логическими элементами на полупроводниковых чипах, обеспечит полный оптический контроль и меньшую стоимость устройства.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ контроля квантового состояния поляритонного кубита | 2023 |
|
RU2821704C1 |
| Способ оптического управления линейной поляризацией излучения | 2022 |
|
RU2801774C1 |
| Способ измерения плотности темных экситонов в полупроводниковых системах экситонных поляритонов | 2023 |
|
RU2816672C1 |
| ПРОГРАММИРУЕМЫЙ ПОЛЯРИТОННЫЙ СИМУЛЯТОР | 2020 |
|
RU2745206C1 |
| УНИВЕРСАЛЬНЫЙ ПОЛНОСТЬЮ ОПТИЧЕСКИЙ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ | 2021 |
|
RU2756257C1 |
| ПОЛЯРИТОННЫЙ ЛАЗЕР | 2015 |
|
RU2611087C1 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ МАКРОСКОПИЧЕСКОГО СОСТОЯНИЯ ПОЛЯРИТОНОВ ПРИ ПОМОЩИ ОДНОГО ФОТОНА | 2020 |
|
RU2782686C2 |
| МЕТОД ПЕРЕКЛЮЧЕНИЯ СОСТОЯНИЯ ПОЛЯРИТОННОГО КОНДЕНСАТА | 2023 |
|
RU2830391C2 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ БОЗОНОВ | 2010 |
|
RU2456671C2 |
| ФЛАКСОННЫЙ БАЛЛИСТИЧЕСКИЙ ДЕТЕКТОР | 2015 |
|
RU2592735C1 |

Изобретение относится к компьютерным системам, в частности к квантовым компьютерам и оптическим логическим элементам для манипулирования данными, и может быть использовано в квантово-механических явлениях, таких как суперпозиция и запутывание. Техническим результатом является формирование и последующее управление квантовыми битами. Способ формирования кубита в плоском полупроводниковом микрорезонаторе заключается в создании при непрерывной нерезонансной оптической накачке двухуровневой квантовой системы на основе бозе-эйнштейновского конденсата экситон-поляритонов в форме незавершенного кольца, где собственными состояниями кубита являются линейные комбинации поляритонных токов, текущих по и против часовой стрелки. 5 ил.
Способ формирования кубита в плоском полупроводниковом микрорезонаторе, заключающийся в создании при непрерывной нерезонансной оптической накачке двухуровневой квантовой системы на основе бозе-эйнштейновского конденсата экситон-поляритонов в форме незавершенного кольца, где собственными состояниями кубита являются линейные комбинации поляритонных токов, текущих по и против часовой стрелки.
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| JP 2011141510 A, 21.07.2011 | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ КУБИТА | 2013 |
|
RU2538296C2 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ БОЗОНОВ | 2010 |
|
RU2456671C2 |
| Устройство для измерения электрических величин | 1959 |
|
SU124026A1 |
Авторы
Даты
2020-03-05—Публикация
2018-12-26—Подача