Заявленное техническое решение относится к области распознавания поврежденных QR-Code.
Из уровня техники известны некоторые способы распознавания различных кодов. Например, из источника информации US 5241164 А (опубл. 31.08.1993) известен способ декодирования символов штрихкода из частичных сканирований, в котором устройство считывания штрих-кода и связанные с ним компоненты сканируют символ штрихкода, создают представление символа и пытаются декодировать это представление, чтобы создать символьное сообщение.
Из источника информации US 7743991 В2 (опубл. 29.06.2010) известен способ работы системы сканирования штрихкода, адаптированной для сборки информации, несущей информацию знаков (IBI), из частичных сканирований данных IBI, которые могут содержать некоторые недекодируемые символы, при этом способ включает этапы: преобразования света, отраженного от цели, в выходные сигналы, представляющие ее; использование датчика изображения; освещение цели с использованием источника освещения; направление света от цели на матрицу датчиков изображения с использованием приемной оптики; определение того, является ли информация, содержащаяся в IBI в пределах цели, полученной из выходных сигналов, декодируемой; передачу изображения IBI на главный процессор, если IBI не декодирован; и размещение процессора, датчика изображения, приемной оптики, источника освещения и дисплея в общем корпусе для ручного управления.
Из источника информации (см. L. Karrach, Е. Pivarciov, and P. Bozeka, Recognition of perspective distorted QR codes with a partially damaged finder pattern in real scene images, Applied Sciences (Switzerland) 10 (21), 1-16 (2020) известен способ распознавания поврежденных QR-Code символов, в котором предлагают восстановить один поврежденный шаблон поиска, чтобы в дальнейшем с помощью трех шаблонов поиска и шаблона наведения получить параметры проективного преобразования.
Однако ни в одном из источников информации не выявлен способ, в котором предлагается определить параметры проективного преобразования для набора опорных элементов, в котором присутствуют не все шаблоны поиска.
Задачей заявленного изобретения является устранение недостатков известного уровня техники. Технический результат заключается в обеспечении способа декодирования QR-Code символов с обрезанными краями, который обеспечивает возможность прочитать содержимое QR-Code в случае его краевого обреза, а также позволяет обеспечить вычисление параметров проективного преобразования, оптимальным способом связывающего образ символа с матрицей кода, а также извлекать матрицу кода и декодировать ее.
Поставленная задача решается, а заявленный технический результат достигается посредством заявленного способа декодирования QR-Code символов с обрезанными краями.
На фигурах представлены:
Фиг. 1: Демонстрация того, что метод, основанный на вычислении параметров проективного преобразования с помощью трех шаблонов поиска и шаблона наведения, не может работать в случае отсутствия двух шаблонов поиска. Слева - образ символа, справа - фиксированная часть QR-Code символа.
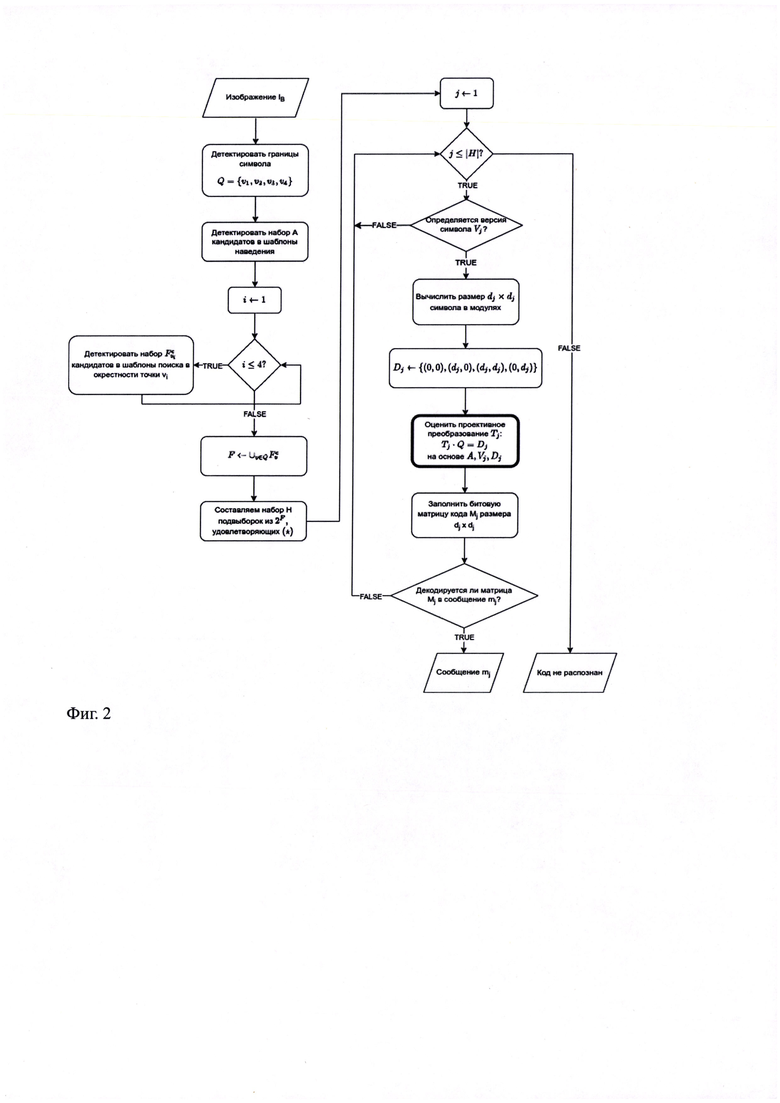
Фиг. 2: Блок-схема предлагаемого метода.
Фиг. 3: Пример найденной границы символа 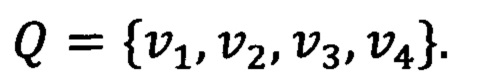
Фиг. 4: Кандидат в шаблоны поиска Fv1, расположенный внутри Q.
Фиг. 5: Набор кандидатов в шаблоны наведения А, найденных внутри Q.
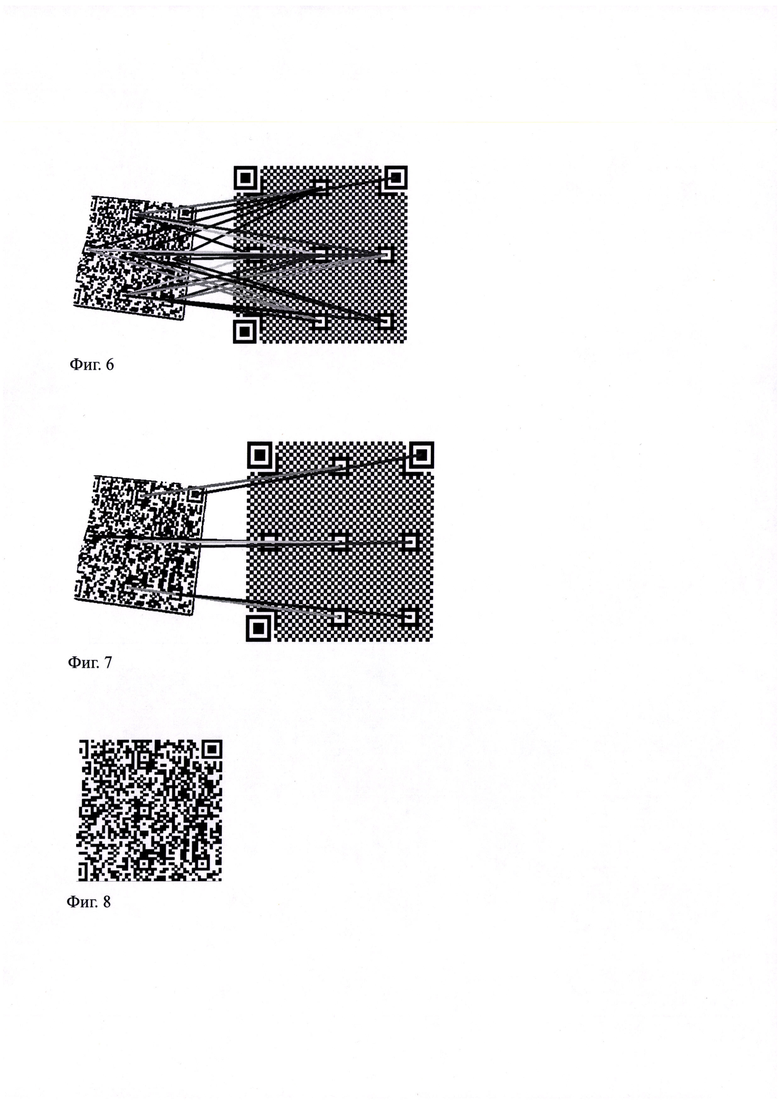
Фиг. 6: Множество всех возможных сопоставлений пар точек.
Фиг. 7: Набор сопоставлений-инлаеров W с наилучшей оценкой Е, по которому вычисляется результирующее проективное преобразование Т.
Фиг. 8: Полученная битовая матрица кода Mj с помощью преобразования Т.
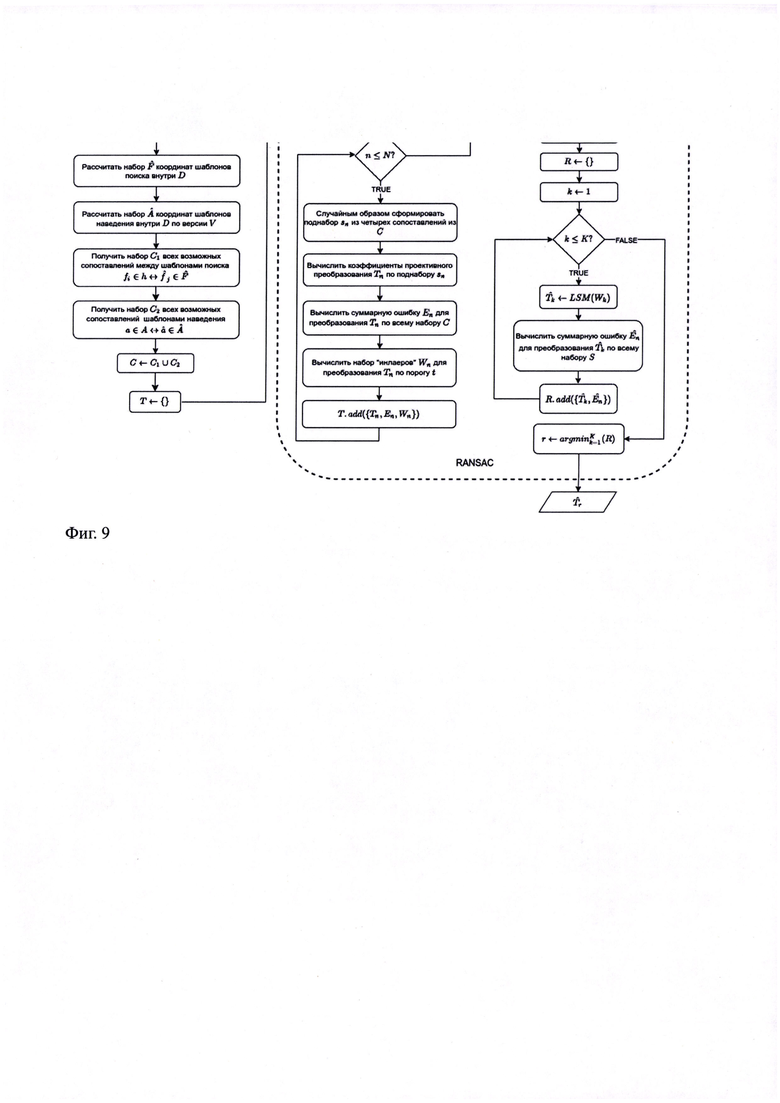
Фиг. 9: Блок-схема алгоритма А1.
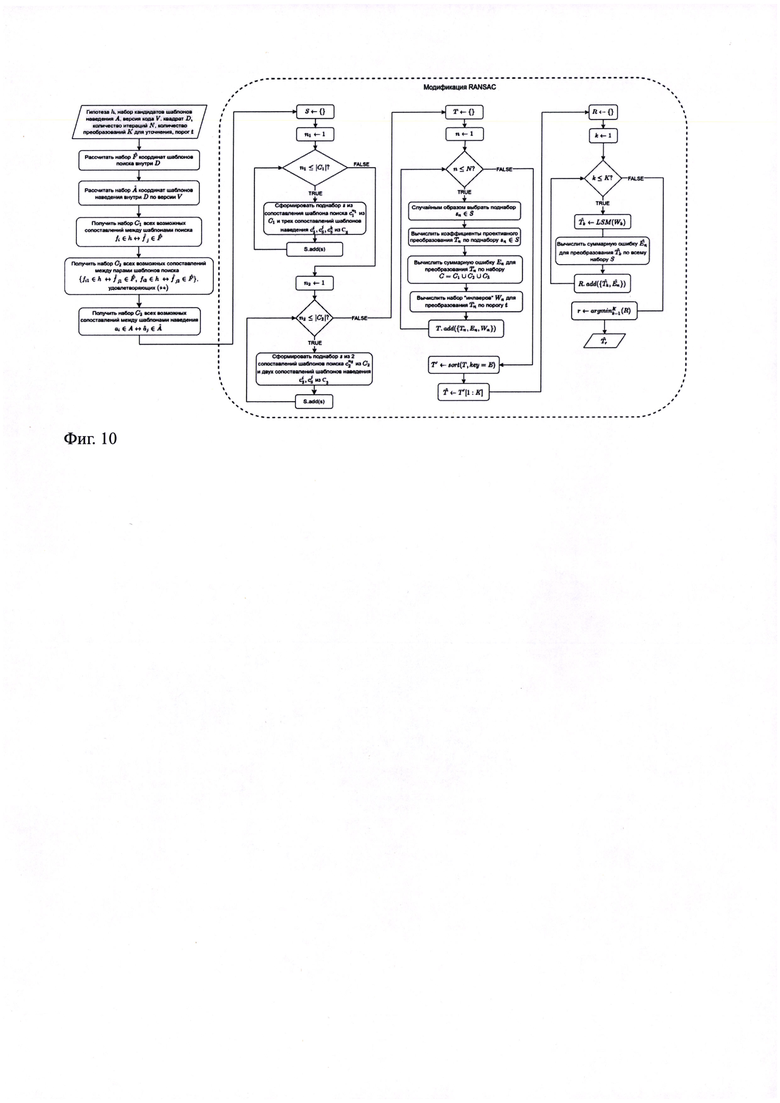
Фиг. 10: Блок-схема алгоритма А2.
QR-Code - специальный графический объект, разработанный для автоматического чтения техническими устройствами, а не человеком. Конкретный графический объект принято называть символом. Для успешного автоматического считывания на входном цифровом изображении требуется установить внутреннюю систему координат образа QR-Code символа. Как правило, для этого нужно вычислить параметры проективного преобразования, переводящего четырехугольник границ образа символа на входном изображении в квадрат его прообраза. Как известно, для определения параметров проективного преобразования необходимо знать корреспонденцию как минимум четырех пар точек. Эти четыре пары обычно являются центрами трех шаблонов поиска и одного шаблона наведения. В случае обреза края штрихкода, воспользоваться таким набором сопоставлений оказывается невозможно, поскольку шаблоны поиска оказываются повреждены и не локализованы (см. фиг. 1). В заявленном решении предложен способ, позволяющий прочитать содержимое символа в случае его краевого обреза.
Первым этапом на входном изображении IB детектируется четырехугольник границ образа символа 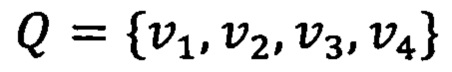 , где vi - его угловая точка. Внутри этого четырехугольника ищется набор А кандидатов в шаблоны наведения. Затем для каждой точки vt детектируются кандидаты в шаблоны поиска, расположенные в ее окрестности. Каждый такой набор кандидатов обозначим как
, где vi - его угловая точка. Внутри этого четырехугольника ищется набор А кандидатов в шаблоны наведения. Затем для каждой точки vt детектируются кандидаты в шаблоны поиска, расположенные в ее окрестности. Каждый такой набор кандидатов обозначим как 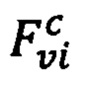 . Четыре полученные множества объединяются в единое множество кандидатов F. Множества А и F включают в себя координаты центров соответствующих кандидатов в шаблоны. Среди элементов множеств могут находиться выбросы - точки, не соответствующие шаблонам на входном изображении. Это обуславливается ошибками работы детекторов шаблонов наведения и поиска.
. Четыре полученные множества объединяются в единое множество кандидатов F. Множества А и F включают в себя координаты центров соответствующих кандидатов в шаблоны. Среди элементов множеств могут находиться выбросы - точки, не соответствующие шаблонам на входном изображении. Это обуславливается ошибками работы детекторов шаблонов наведения и поиска.
Обозначим множество всех возможных выборок шаблонов поиска как 2F. Рассмотрим
- подвыборка состоит из одного, двух или трех шаблонов поиска,
- подвыборка не может включать два или более шаблона из одного  множества
множества 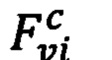
набор Н подвыборок из 2F, удовлетворяющих ограничениям:
Будем последовательно рассматривать все элементы-гипотезы из множества Н. Для очередной гипотезы hj ∈ H, где j ∈ {1,| …, |H|}, по входному изображению определим соответствующий ей номер версии QR-Code символа Vj. Если номер версии вычислить не удалось, цикл переходит к следующей гипотезе.
Обозначим бинарную матрицу, являющуюся прообразом рассматриваемого символа, как Mj. Каждый элемент этой матрицы соответствует значению одного модуля символа. По номеру версии согласно спецификации символики QR-Code [1] однозначно определяется размер dj матрицы Mj. Также зададим квадрат Dj, соответствующий размерам матрицы: Dj={(0,0), (dj, 0), (dj, dj), (0, dj)}.
Для того чтобы получить значения матрицы Mj, необходимо оценить проективное преобразование Tj, переводящее угловые точки четырехугольника Q в квадрат Dj:Tj⋅Q=Dj. Это преобразование позволяет вычислить координаты центров модулей на входном изображении IB и, следовательно, определить цвет модулей.
Оценка преобразования может быть осуществлена различными способами и на основе разных данных. Наиболее полным набором возможных входных параметров являются: набор из гипотезы hj, множество кандидатов в шаблоны наведения А, номер версии Vj и квадрат Dj. Два конкретных алгоритма оценки проективного преобразования А1 и А2 описаны далее.
Установив связь координат между образом и прообразом посредством Tj, заполним битовую матрицу кода Mj. Из нее согласно спецификации символики QR-Code [1] извлекается последовательность байт, подаваемая на вход декодеру. Если сообщение ml успешно декодировано, то перебор завершается, а само сообщение выдается в качестве результата работы метода. Иначе происходит переход на следующую итерацию. Если все гипотезы не привели к результату, то прочитать код не удалось.
Блок-схема описанного метода представлена на Фиг. 2.
Теперь, когда описана общая схема метода, приведем два алгоритма, А1 и А2, вычисления коэффициентов проективного преобразования Т. Место данных алгоритмов в общей блок-схеме (Фиг. 2) выделено жирной обводкой. На вход им подается гипотеза h ∈ Н, версия кода V, квадрат матрицы кода D и множество задетектированных шаблонов наведения А. На выходе оба алгоритма выдают лучшую оценку преобразования  , соответствующую гипотезе. Заметим, что набор положений шаблонов поиска из F фиксируется альтернативой h.
, соответствующую гипотезе. Заметим, что набор положений шаблонов поиска из F фиксируется альтернативой h.
Алгоритм A1
По версии кода V, согласно спецификации [1], установим количество и геометрическое расположение шаблонов наведения 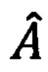 , а также положение шаблонов поиска
, а также положение шаблонов поиска 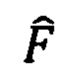 на прообразе символа. Фактически, координатами шаблона являются номера строки и столбца матрицы Mj, соответствующие центральному модулю шаблона. Для определения проективного преобразования требуется четыре сопоставления точек на двух изображениях. В данной задаче особую сложность вызывает тот факт, что шаблоны поиска, как и шаблоны наведения, идентичны между собой. Это значит, что невозможно определить, какому шаблону поиска (наведения) на прообразе символа Mj соответствует детектированный шаблон поиска (наведения) на растре исходного изображения IB. Кроме того, множество А кандидатов в шаблоны наведения может содержать точки-выбросы. В таком случае необходимо построить и проанализировать набор С всех возможных сопоставлений шаблонов поиска между h и
на прообразе символа. Фактически, координатами шаблона являются номера строки и столбца матрицы Mj, соответствующие центральному модулю шаблона. Для определения проективного преобразования требуется четыре сопоставления точек на двух изображениях. В данной задаче особую сложность вызывает тот факт, что шаблоны поиска, как и шаблоны наведения, идентичны между собой. Это значит, что невозможно определить, какому шаблону поиска (наведения) на прообразе символа Mj соответствует детектированный шаблон поиска (наведения) на растре исходного изображения IB. Кроме того, множество А кандидатов в шаблоны наведения может содержать точки-выбросы. В таком случае необходимо построить и проанализировать набор С всех возможных сопоставлений шаблонов поиска между h и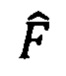 , и сопоставлений шаблонов наведения между А и
, и сопоставлений шаблонов наведения между А и 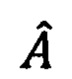 (Фиг. 6).
(Фиг. 6).
Набор С по построению содержит большое количество ложных сопоставлений. Для определения параметров проективной модели предлагается использовать схему RANSAC [2], устойчивую к выбросам в данных. RANSAC предполагает случайный выбор N минимальных поднаборов сопоставлений sn, по которым считаются параметры преобразований-гипотез Tn. Для каждой гипотезы выделяется поднабор инлаеров Wn, то есть поднабор сопоставлений из С, удовлетворяющих гипотезе с некоторой заранее заданной точностью.
Также для каждой гипотезы подсчитывается оценка En согласованности преобразования-гипотезы Tn и данных С. Будем называть значение En суммарной ошибкой. В исходном алгоритме RANSAC оценка представляет собой количество инлаеров. Также существует оценка MSAC [3], которая вычисляется как сумма усеченных по порогу t квадратов расстояний от центров шаблонов на прообразе символа Mj до преобразованных гипотезой Tn шаблонов на растре IB. В работе [3] было экспериментально показано, что эта оценка при выборе лучшего преобразования точнее той, что используется в исходной работе [2], посвященной RANSAC. Существуют и другие оценки, которые можно использовать на данном этапе.
Затем выбирается K гипотез с наименьшей оценкой. При необходимости для каждой k-ой гипотезы коэффициенты преобразования итеративно пересчитываются с помощью методов решения переопределенных систем по соответствующему набору инлаеров Wk. После этого повторно проводится оценка суммарной ошибки каждого полученного преобразования и выбирается то, которое имеет наименьшую ошибку. Блок-схема алгоритма 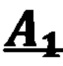 представлена на Фиг. 9.
представлена на Фиг. 9.
Алгоритм A2
Этот алгоритм отличается от предыдущего способом формирования минимальных поднаборов sn. Алгоритм А1 использует поднаборы, составленных из любых сопоставлений из С. При этом набор С по построению содержит много выбросов. В таком случае необходимо большое количество итераций, чтобы обеспечить высокую вероятность получения верной оценки преобразования Т.
Рассмотрим по отдельности наборы С1 и С2 сопоставлений шаблонов поиска и шаблонов наведения соответственно. Набор С1 сопоставлений шаблонов поиска в подавляющем большинстве случаев имеет меньший процент выбросов по сравнению с сопоставлениями шаблонов наведения из С2. В таком случае, требование присутствия в поднаборе sn сопоставлений шаблонов поиска увеличит вероятность выбора подходящего поднабора сопоставлений. Это позволит уменьшить количество итераций, необходимых для получения верной оценки преобразования с высокой вероятностью. Здесь мы указали только значительное отличие второго алгоритма. Полная блок-схема алгоритма А2 приведена на Фиг. 10.
Для использования схемы RANSAC требуется задать параметры N, K и t, которые таким образом, также становятся входными параметрами алгоритмов А1 и А2. По поднаборам, состоящим из трех или менее сопоставлений, определить проективное преобразование невозможно. При этом метод должен обеспечить чтение символа кода даже при наличии только одного шаблона поиска на входном изображении. Поэтому возникает ограничение на наличие на QR-Code символе трех или более шаблонов наведения. Согласно спецификации [1], этим ограничениям удовлетворяют версии QR-Code с 7 по 40 включительно.
Таким образом, сущность заявленного технического решения заключается в том, что для установления внутренней системы координат символа кода при обрезке хотя бы одного из шаблонов поиска следует использовать шаблоны наведения. При этом суммарное количество шаблонов поиска и наведения может оказаться избыточным. Таким образом, возникает комбинаторная задача выбора оптимального набора сопоставлений шаблонов. Решение данной задачи позволяет вычислить параметры проективного преобразования, наилучшим способом связывающего образ символа с матрицей кода. Применение проективного преобразования тогда позволяет извлечь матрицу кода и, соответственно, декодировать ее.
Список литературы
1. Information technology - Automatic identification and data capture techniques - QR Code bar code symbology specification, standard, International Organization for Standardization (2015).
2. Fischler, M.A. & Bolles, R.C. (1981). Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24 (6), 381-395. https://doi.org/10.1145/358669.358692
3. Torr P.H.S., Zisserman A. MLESAC: A new robust estimator with application to estimating image geometry // Computer vision and image understanding. - 2000. - T. 78. - 1. - C. 138-156.


Изобретение относится к распознаванию поврежденных QR-Code. Технический результат заключается в обеспечении способа декодирования QR-Code символов с обрезанными краями, который обеспечивает возможность прочитать содержимое QR-Code в случае его краевого обреза. Заявленный способ декодирования QR-Code символов с обрезанными краями заключается в том, что первым этапом на входном изображении IВ детектируется четырехугольник границ, внутри которого ищется набор А кандидатов в шаблоны наведения, затем для каждой точки vi детектируются кандидаты в шаблоны поиска, расположенные в ее окрестности, четыре полученные множества объединяются в единое множество кандидатов F, далее последовательно рассматривают все элементы-гипотезы из множества Н, которое включает подвыборку, которая состоит из одного, двух или трех шаблонов поиска, и подвыборку, которая не может включать два или более шаблона из одного множества для очередной гипотезы, по номеру версии согласно спецификации символики QR-Code однозначно определяют размер бинарной матрицы, далее вычисляют координаты центров модулей на входном изображении и определяют цвет модулей, устанавливают связь координат между образом и прообразом, заполняют битовую матрицу кода Mj, далее из нее согласно спецификации символики QR-Code извлекают последовательность байт, подаваемую на вход декодеру. 10 ил.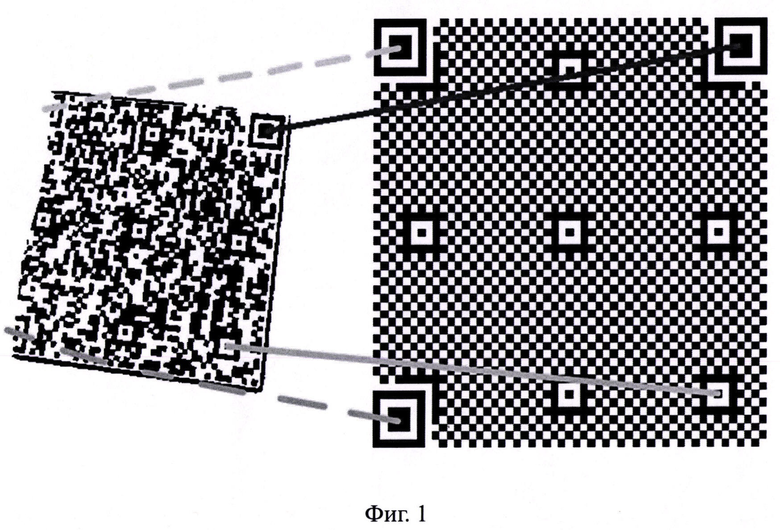
Способ декодирования QR-Code символов с обрезанными краями, заключающийся в том, что первым этапом на входном изображении IB детектируется четырехугольник границ образа символа 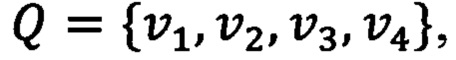 где vi - его угловая точка, внутри этого четырехугольника ищется набор А кандидатов в шаблоны наведения, затем для каждой точки vt детектируются кандидаты в шаблоны поиска, расположенные в ее окрестности, четыре полученные множества объединяются в единое множество кандидатов F, при этом множества А и F включают в себя координаты центров соответствующих кандидатов в шаблоны, далее последовательно рассматривают все элементы-гипотезы из множества Н, которое включает подвыборку, которая состоит из одного, двух или трех шаблонов поиска, и подвыборку, которая не может включать два или более шаблона из одного множества
где vi - его угловая точка, внутри этого четырехугольника ищется набор А кандидатов в шаблоны наведения, затем для каждой точки vt детектируются кандидаты в шаблоны поиска, расположенные в ее окрестности, четыре полученные множества объединяются в единое множество кандидатов F, при этом множества А и F включают в себя координаты центров соответствующих кандидатов в шаблоны, далее последовательно рассматривают все элементы-гипотезы из множества Н, которое включает подвыборку, которая состоит из одного, двух или трех шаблонов поиска, и подвыборку, которая не может включать два или более шаблона из одного множества 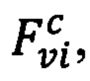 для очередной гипотезы hj ∈ Н, где j ∈ {1, …, |Н|}, по входному изображению определяют соответствующий ей номер версии QR-Code символа Vj, при этом если номер версии вычислить не удалось, цикл переходит к следующей гипотезе, по номеру версии согласно спецификации символики QR-Code однозначно определяют размер бинарной матрицы Mj, которая является прообразом рассматриваемого символа, далее вычисляют координаты центров модулей на входном изображении IB и определяют цвет модулей, устанавливают связь координат между образом и прообразом, заполняют битовую матрицу кода Mj, далее из нее согласно спецификации символики QR-Code извлекают последовательность байт, подаваемую на вход декодеру, при этом если сообщение mj успешно декодировано, то перебор завершается, а само сообщение выдается в качестве результата работы метода.
для очередной гипотезы hj ∈ Н, где j ∈ {1, …, |Н|}, по входному изображению определяют соответствующий ей номер версии QR-Code символа Vj, при этом если номер версии вычислить не удалось, цикл переходит к следующей гипотезе, по номеру версии согласно спецификации символики QR-Code однозначно определяют размер бинарной матрицы Mj, которая является прообразом рассматриваемого символа, далее вычисляют координаты центров модулей на входном изображении IB и определяют цвет модулей, устанавливают связь координат между образом и прообразом, заполняют битовую матрицу кода Mj, далее из нее согласно спецификации символики QR-Code извлекают последовательность байт, подаваемую на вход декодеру, при этом если сообщение mj успешно декодировано, то перебор завершается, а само сообщение выдается в качестве результата работы метода.
| Способ формирования и декодирования двумерного кода носителя информации | 2023 |
|
RU2823438C1 |
| СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ В ВИДЕ УЛЬТРАСЖАТОГО НАНОБАР-КОДА (ВАРИАНТЫ) | 2013 |
|
RU2656734C2 |
| EP 3330885 B1, 07.10.2020 | |||
| US 2016140374 A1, 19.05.2016 | |||
| CN 113935448 A, 14.01.2022. | |||
Авторы
Даты
2025-04-07—Публикация
2024-08-15—Подача