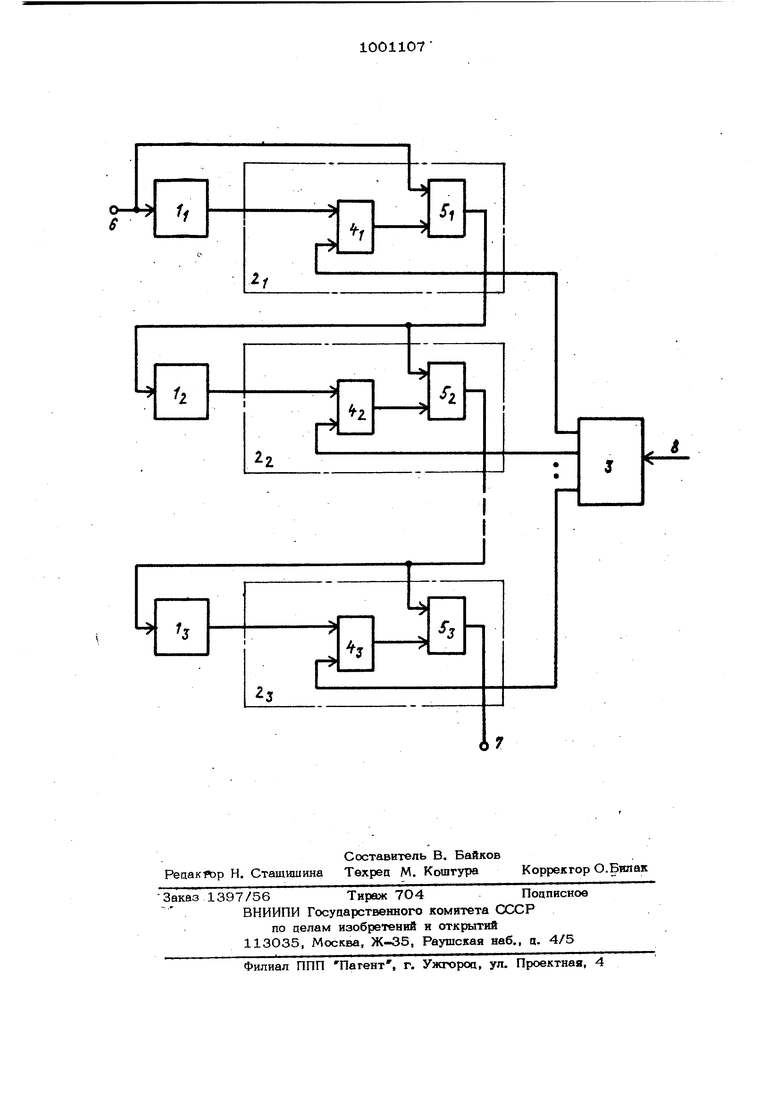
Изобретение относится к математике и вычислитепьной текнике и прррназнпче но для нахожрения коэсЬФициентов разложения двоичной последовательности в базисе Жегалкина, а также для отыскания канонической формы представления переключательной функции в виде полино ма Жегалкина. Известен анализатор спектра, содерж щий аналого-цифровой преобразователь, регистр сдвига, сумматоры, умножитель, элементы И, блок управления {1 Этот анализатор осуществляет разло.жение сигналов в базисе функции Хаара и не может использоваться для нахождения коэффициентов разложения в базисе Жегалкина. Наиболее близким к предлагаемому по техническому решению является анализа- тор спектра, содержащий элементы зацержки, арифметические блоки, состоящие из сумматоров-вычитателей и блок управ ления 1 . Недостатком известного устройства является то, что оно не может быть использовано для анализа спектра сигналов в базисе Жегалкина. Цель изобретения - расширение функциональных возможностей за счет полу чения спектра двоичной последовательности в базисе Жегалкина. Поставленная цель достигается тем, что анализатор спектра, содержащий П элементов задержки (п -порядок систе- мы базисных функций),т арифметических блоков, причем вход и выход -го ( 1 1 - п ) элемента задержки соединены соогветствеино с первым и вторым информационными входами i -го арифметического блока, выход -i -го арифметического блока, кроме п -го, подключен к первому информационному входу ( i + 1)го арифметического блока, первый информационный вход первого арифметического блока и выход п -го арифметического блока являются соответственно входом и выходом анализатора спектра, содержит п -разрядный счетчик, вход которого является тактовым входом анализатора спектра, а выход i -го разряда ( 1 - И , нумерация со стороны младших разрядов) подключен к управляющему входу 1 -го арифметического блока, каждый арифметический блок состоит из элемента И и сумматора по модулю два, первые входы сумматора по модулю два и элемента И являются первым и вторым информационными входами соответствующего арифметического блока, . второй вход элемента И является управл ющим входом арифметического блока, вь1ход элемента И подключен к второму входу соответствующего сумматора по модулю два, выход когорого является выходом соответствующего арифметического блока. На чертеже представлена функциональ ная схема анализатора спектра. Он содержит элементы 1 зaдepжки счетчик 3. арифметические блоки 2( Арифметические блоки состоят из элемен- тов И 4,.„ и сумматоров 5 по модулю два. Позициями 6-8 обозначены информационный вход-выход и тактовый вход анализатора спектра соответственно, Элемент 1 задержки задерживает двоичную последовательность на такт. Каждый последующий элемент 1„ задержки осуществляет вдвое больщую задержку, чем предыдущий. Рассмотрим алгоритм вычисления коэффициентов полинома Жегалкина, реализуемый предлагаемым устройством. Пусть задана последовательность дли- ны где f NfcoKer быть или нулем, или едини цей С j 0,1 ... , 2 -1 ) (добавлением соответствующего числа нулей длину последовательности всегда можно сделать степенью двойки). Двоичная функция f (-t) , задаваемая 2 -компонентным вектором значений разложима в ряд конечной длины Аft к --Ки
назьшаемый полиномом Жегалкина, где (Ь , ... ,tn ) и (К , ... , К) - запись величин t и К (Oi-t 2 1-
i 1
в двоичной системе счисления);
t z %+--b2t
.
1 1
Если в (2) положить (,1, О,
2 1, з 0 4 0 5 1. «6 1, «т О, то приходит к полиному Жегалкина
®t,
m ®
f(t)1l Z - знак суммы по модулю два, а i. . 1, если О, Величины рц могут быть или нулями, или единицами. Например, при п 3 имеем полином Жегалкина следующего вида: (t) F(o)® F(l)(2))i2S® ® F(4) t ® f(5) 0F(fe) 0 ©Fdlt t t, . где(- знак суммы по модулю два. Чтобы получить вектор коэФфициен- - , необходимо вектор умножип -ую кронекерову степень матри1 . О Обратный переход от вектора коэффициентов F(K)K вектору значений функции f(.t) также осуществляется посредством умножения на п -ую кронекерову степень матрицы (1). Для нахождения п -ой кронекеровой степени матрицы (1) можно воспользоваться следующим рекурентным соотношением:К-1 К-1 При п 3 умножение вектора значений функции па матрицу И„ записывается так: аля которого F(0)l, F(|)1, FU)0, F(3 О. F(4)l. Fl5)0. F(b)l. Fn)0. Соотношение (2) можно .представить как систему сле;1ующих равенств, записанных в скобочнсй форме: . F(o)-f FHbf. F(i)f2 Р(3){з © (J® fiU-oi F(4)®Q®0 Fl5)fjrf F(b) ®{f2®0 F(-|--fT®U6)G), 5-Л)® л®(о)Для п 3 алгоритм функционирования предлагаемого устройства определяется системой равенств (З). В каждом из восьми последовательных тактов формируется значение соответст вуюшего коэффициента полинома Жегалкина. Как следует из (З), произвольный коэффициент F(K) представляет собой сумму по моаулю два четырех слагаемых которыми являются элемент входной последовательности f. к величины с выхоДОБ элементов задержки 1-, , lo , la Причем величины с выхода элемента 1/ адержки (заключены в круглые скобки) участвуют в формировании каждого второ ,, коэффициента, величины с выхода элемента 1. задержки (в квадратных скобках) суммируются только в третьем, четвег том и седьмом, восьмом тактах, величины с вькоаа элемента 1 задержки (в фигурных скобках) необходимы в пятом, шестом, седьмом и восьмом тактах. Поэтому управление первым, вторым и трет t,w «г,„А.,с„«и «покя и S) полт, им арифметическими блоками 2 осушест вляется, соответственно, посредством сигналов с выходом младшего, среднего и старшего разрядов счетчика. В каждом такте в элемент задержки i засылается элемент входнсА послецо 10 076 вательности, в элемент 12 задержки сумма по моаулю ава первых цвух слага емых из соответствующего равенства системы (3), а в элемент 11 зацержки - сумма первых трех слагаемых. В течение первого такта соаержимое счетчика 3 составляет (ООО). Поэтому, сигналы с выхоаов элементов зацержкя 1 - 3 ® проходят через элементы И 4 - 4 , и коэффициент F (О) TCfflcaeciw венен элементу f входной последовательности, который записьтается в элемент задержки 1 - la . Во втором такте на управлякюем входе арифметического блока 2 присутствует логическая единица, вследствие чего коэффициент Р является суммой по модулю два элемента , последовательности на входе 6 и величины Q , храннЕмой в элементе Г задержки. В Элементе 1х - la задержки засыпаются соответственно ,-, В третьем такте единичный потенциал поступает на управляющий вход арифметического блока 22 , который к символу последовательности на входе 6 прибавляет по модулю два элемент f Q , хранившийся два такта в элементе 12 задержки. Величина с входа 6 записывается в элемент 1 задержки, а величины и fjOfpC выходов сумматоров 5 и 5 соответственно поступают в элементы Ij и 1 задержки. В течение четвертого такта на выходах «вух младших разрядов счетчика 3 присутствуют логические единицы, обеспечиваюшие прибавление к элементу f последовательности на входе 6 величины 2 поступаюших с выходов элементов задержки 1 и 12 . На выходе 7 имеем сумму .no окончании такта в элементы l-f - 1азадержки записьшаюгся величины ®f/i ® f. (+)F« соответственно, г характеризуется появлени единицы только на выходе старшего счетчика 3. Поэтому, к символу последовательности прибавляегся по модулю два величина SQ ,, четыре хранившаяся в элементе l задерж«И. Следовательно, на выходе 7 имеем (Q. Величина засылается одновр)е- «««« ° элементы 1-, - Ij задержВ шестом такте в формировании сумы участвуют величины . и ({ с выходов элементов Ц и 1 зацержки, а тйкже элемент fc ® :0По ок чании такта в элементы 1,-12 задерж ки записываются величины f,. ,f fyOf соответственно, В течение седьмого такта содержимо счетчика 3 составляет (110), и поэтом информация считывается с выходов элементов Irt и 1, задержки, на которых присутствует величины (А и f- соответственно. Сумма на выхоце 7 равна (,0 4® 2 о-Величины fg , 4 Ь© записываются в элементы 1 - 1 задержки. Восьмой такт, отличается тем, что в формировании суммы участвуют величины с выходов всех элементов 1 - - 1- заде жки. Таковыми являются f, i® ( f f выходе 7 усгройсгва Э З®%® ® 0имеем f-,®(®%€ ,,v 1 - 1, задержки засылаются элементы величины €,® , f-,0fe,@f 50 4Таким образом, в восьми последовательных тактах на выходе 7 устройства получаем коэффициенты F (О), F (1), Р(2), F(3). F(4), F(5), F(6), F (7 ) полинома Жегалкина. Таким образом, технико-экономический эффект от использования предлагаемого устройства состоит в. возможности автоматизировать процесс получения коэффициентов разложения двоичной последовательности в базисе Жегалкина. Спектр последовательности длины 2 вычисляется за 2 тактов, г.е. по окончани последовательности сразу имеем ее коэф фициенты разложения. Формулаизобретения Анализатор спектра, содержащий h элементов задержки ( И - порядок систе МЫ базисных функций), п арифметических блоков, причем вход и выход i -го ( 1 - tt) элемента задержки соединены соответственно с первым и вторым инфор мационными входами i -го арифметического блока, крюме п -го, подключен к первому информационному входу ( i + 1)- го арифметического блока, первый информ мационный вход первого арифметического блока и выход п -го арифметического блока являются соответственно входом и выходом анализатора спектра, отличающийся тем, что, с целью расширения функциональных возможностей за счет получения спектра двоичной последовательности в базисе Жегалкина, он содержит п -разрядный счегчик, вход которого является тактовым входом анализатора спектра, а выход i-го разряда ( i 1 - м , HyivtepaHHH со стороны младших разрядов) подключен к управляющему входу i -го арифметического блока, каждый арифметический блок состоит из элемента И и сумматора по модулю два, первые входы сумматора по модулю два и элемента И являются первым и вторым информационными входами соответст вукицего арифметического блока, второй вход элемента И является управляющим входом арифметического блока, выход элемента И подключен к второму входу соответствующего сумматора по модулю два, выход которого является выходом соответствующего арифметического блока. Источники информации, принятые во внимание при экспертизе 1.Авторское свидетельство СССР № 579623, кл, Об F 15/332, 1975. 2.Авторское свидетельство СССР .№ 5554О4, кл. 6 06 F 15/20, 1975 (прототип).



| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь | 1983 |
|
SU1140130A1 |
| Устройство для вычисления свертки в базисе Жегалкина | 1981 |
|
SU1014126A1 |
| Устройство для разложения цифровых сигналов по Уолшо-подобным базисам | 1983 |
|
SU1108461A1 |
| Функциональный преобразователь | 1986 |
|
SU1339583A1 |
| Магнитооптическое устройство для реализации дискретного преобразования Фурье | 1990 |
|
SU1795472A1 |
| Устройство для ортогонального преобразования цифровых сигналов по функциям Хаара | 1983 |
|
SU1116435A1 |
| Процессор для преобразования цифровых сигналов по Хааро-подобным базисам | 1984 |
|
SU1168966A1 |
| Цифровой анализатор спектра в ортогональном базисе | 1983 |
|
SU1124326A1 |
| Анализатор спектра в ортогональном базисе | 1989 |
|
SU1615740A1 |
| Функциональный преобразователь | 1986 |
|
SU1388890A1 |


Авторы
Даты
1983-02-28—Публикация
1981-08-14—Подача