Изобретение относится к специализированным средствам вычислительной техники и может быть применено для определения характеристик случайных процессов и диагностики различных объектов.. Известно устройство,содержащее блок задания начальных условий, блок сравнения, блок анализа гипотез, блок формирования, блок управления t . К недостаткам устройства следует отнести низкое быстродействие, обус ловленное примененным методом анали а также его сложность. Наиболее к предлагаемом изобретению является устройство, со держащее блок задания начальных усл вий, блок сравнения, блок анализа гипотез, блок определения разности отклоненийJ реверсивный счетчик, блоки элементов И формирователь импульсов элемент ШЖ |2j . К недостаткам известного устройс ва следует отнести низкую достоверность и точность измерения. Выбор Нл (Нл - гипотеза между гипотезa ш процесс нестационарен при убывании значений Хр и Н (Н - гипотеза процесс нестационарен при возрастан jXj), приводит к сшибкам. Для уменьшения этих ошибок-необходимо ввести коэффициенты вероятности ошибки оС. и и на каждой стадии эксперимента вычислять отношение вероятностей Р/ Р и сравнивать с заранее выбранными постоянными величинами А и В. Все это усложняет сам метод вычислений и снижает его достоверность. Целью изобретения является повьт ние точности и достоверности и уирощ
ние конструкции.
Поставленная цель достигается тем, что устройство для определения стационарности случайного процесса, содержащее блок определения разности и блок регистрации, содержит первый и второй фазовращатели, первый и второй детекторы, фильтр нижних частот, делитель напряжения, группу согласующих элементов, например катодных повторителей, блок определейия среднеквадратичного отклонения и группу из последовательно соединенных элементов задержки, вход первого из которю:: объединен с входами первого фазовращателя, блока определения среднеквадратичного отклонения и является входом устройства, а выход каждого элемента задержки через соответствуюгде га - число элементов задержки (га 5-10), С выходов фазовращателя 1 и элементов 3 задержки сигнала через группу соглас5«ощих элементов 4 поступает на вход блока 5 определения разности (суммирующего усилителя), где происходит cy 0 mpoвaниe сигналов
()l4«l(HC),lit + 2t),...,z(t+wC),
как по ансамблю, так и по времени. Суммарный сигнал с выхода блока 5 поступает на вход детекторов 6 и 7 и второго фазовращателя 2, где происхо.дит взятие суммарного сигнала по модулю. После прохождения через о фильтр нижних частот 8 на выходе получают сигнал, пц опорциональный средщий согласующий элемент подключен к первому входу блока определения разности, второй вход которого соединен с выходом первого фазовращателя, а выход блока определения разности через первйй детектор и через последовательно соединенные второй детектор и второй фазоврап1атель подключен к входу фильтра нижних частот, выход которого соединен с первым входом делителя напряжения, второй вход которого подключен к выходу блока определения среднеквадратичного отклонения, а выход делителя напряжения соединен с входом блока регистрации. На чертеже приведена структурная схему устройства. Устройство содержит фазовращатели 1 и 2, групцу элементов задержки 3, группу согласующих элементов 4, , блок 5 определения разности, детекторы 6 и 7, фильтр 8 нижних частот, делитель 9 напряжения, блок 10 определения среднего квадратичного отклонения (СКО) и блок 11 регистрации. Устройство работает следующим образом. На вход устройства подается напряжение, пропорциональное исследуемому процессу Z (t). С входа устройства сигнал одновременно поступает на фазовращатель 1, группу элементов 3 задержки и блок 10 определения СКО. В фазовращателе 1 происходит сдвиг сигнала на угол (f 180, что равносильно его умножению на -1. Проходя через группу элементов 3 задержки, сигнал задерживается последовательно о л .л на время г К- у у нему значению модуля суммы сигналов Этот сигнал поступает на вход делителя 9, на второй вход которого пост пает сигнал с блока 10 вычисления среднего квадратичного отклонения исходного процесса (dj). В блоке 9 происходит деление СКО исходного про цесса 6- на среднее значение модуля суммы сигналов jUa . сигнал, пропорциональный этому частному, поступае на блок 11. Принцип действия устройства заключается в следующем. Если процесс стационарен, то для соответствующего закона распределения случайной величины отношение среднего квадратичного отклонения 6j. к среднему аначению модуля разности исходного процесса и ансамбля процессов, сдвинутых ня воемя k. где k 1,2,3,..., m at- шаг квантования, является вел чиной постоянной. Например, для нор мального случайного процесса эта величина (назовем ее коэффициентом стационарности) равна z 2. |5- 0886, для процесса с равномерным законом распределения случайной ве;;1ичины для процесса с распределением случайной величины по закону арксинуса ,875, т.е. во всех случаях 0,9. Для линейной функции (линейного тре да) этот коэффициент стационарности будет представлять собой зависимост Т„ Л 9.577 -- , где Тр - длительность реализации; mt конечная величина сдвига функции. Обычно такой сдвиг меньше 0,1, т.е. , Тр. Тогда коэффициент стационарности будет равен ,77, т.е. резко отличиется от стационарны процессов. Причем oi не зависит от крутизны линейной функции, т.е. от коэффициента а (и at+b), как это будет показано ниже. Теоретические и экспериментальные,данные дают основание считать, что если об 0,9, то процесс нестационарный, а если 0.0,9, то процесс стационарный. Для иллюстрации вьшесказанного озьмем смешанный аддитивный процесс z(tVY(tHXli)4uU), гдеУ(1) - случайная состанляющая процесса (белый шум) с |U,j 0 ибу i 1; X(t)- гармоническая составляющая XltbX in +i ; ( - детерминированная функция, например, составляющая линейный тренд U(t)at+b, где а к Ь, постоянные еличины. В основу анализа положим ледующую функцию: I 12.111-Zit+t)Ut, (3) - длительность реализации; сдвиг функции относительно начала отсчета; конечный сдвиг функции (в нашем случае t m) , которую назовем модульструктурной функцией. С целью простоты анализа рассмотрим процесс преобразования чисто случайного процесса с нормальным законом распределения случайной величины. Как известно, плотность вероятности случайной величины Y(t) распределенной по нормальному закону выражается формулой: (математическое ожидание случайной величины; 1 нашем дисперсия случайной величины. В нашем случае мы имеем дело с композицией двух нормальных распределителей Y (t) и Y (t+J) . Если через 6 (t,с) обозначить eyl.u)-Y(t)-Y(i.). то распределение функции бц (t ,J) примет следующий вид: 2. так как случайная величина (t,) представляет србой композицию нормально распределенных величин Y(t) и (t+J,), то следовательно, случайная 5 величинаЕ (t/) также распределена . 2 о,-г нормально с i(g /Uy О и6р 2бц. Взятие по модулю распределения композиции случайных величин yV l yv, )))| (6) приводит к существенному изменению распределения плотности вероятности л2 -2 .. где всегда ,, 0. в данном случав математическое ожи13 t-frtTni 4 f ftA «лs rrtftKff ллагм- дание будет равно , (U« 6. 24Jdu 1.13ciu. (8) 1 ( е К N Н У и в свою очередь |Un является первой точко1 модуль-структурной функции () Lf), Проводя сдвиги исходного процесса на 2С, 3,..., kc,... m-J, получаем соответственно точки модуль-структурной функции 1,2, b-j, ..., L, ,.., L Так как . L (kC) является выборочной оценкой математического ожидания р, то тематическое ожидание л л Г 1 л rV 1 .(u.,,,,,, является несмещенной оценкой центра распределения модуля случайной функцин (6). Таким образом, jUц |Uq , cлвдoвaтeльнo :, откуда 6(1 -iRF N - i 0,886. (10) Аналогично можно определить об для стационарного случайного процесса с равномерным законом распределения случайной величины 6 -Г -i а также для распределения случайной величины по закону арксинуса. Синусоидальные колебания со случайной фазой (распределение арксинуса) также являются стационарным процессом. 1096666 Осуществив преобразования, получимQ (ttl |e ( 1кп с B отличие от ранее рассмотренной величины flf. , зависящей только от текущего времени t,( , кроме того, зависит от сдвига функции . Произведя очевидные преобразования под знаком модуля (12), получим ,.(,..„ .„..„(-,2|1)|/ Х. ..| -6i«2 coa25-co5 |i. («) 1 Для определения точек модуль структурной функции необходимо проинтегриРовать выражение (13) тя т/2 ( ,&)dt -( о . 2 (л q (14) 3 п-:р-со5-: co&-;ps,n--- jt тем, чтобы освободиться от знака „оду,ядпода„тегральной функции (14) проинтегриру ем в небольших пределах значение в пределах от (начального значения аргумента) iu. , до (конеч„о о значения аргумента) t, , когда разность имеет неизменный знак (+) или (-) ,,.,, j I I Hl Опуская промежуточные преобразования, запишем 2Уц,Г 2iJSf 2iJi . 27t L t -:p- co9-j5in-dfc- ; n-Y-Jeos-: dttmi, f jil-.(,5, 2irt Проведя замену переменных ( Т dt du -) и представив пределы 2 t интегр1 рования t +- и - Т .вычислим интегралы в выражении (15), Запишем окончательный результат i (-juZlJ . П 6) ;i Т Среднее значение модуль-структурной функции определится, как Ч( . Ift . Теперь определим коэффициент стационарности для синусоидальной функции . ji j a874. (18 ( Итак, для заведомо стационарных процессов, коэффициент стационарности оС находится в пределах Л 0,866-0,886 т.е. О 4С 0,9. При наличии в исходном процессе нестационарности по математическому ожиданию коэффициент стационарности об резко возрастает. Рассмотрим, например, наиболее простой случай линейного тренда, описываемого линейной функцией и (t) - at+b,(19 где а и b - постоянные величины; t - аргумент Хвремя). Преобразование линейной функции (19) при помощи модуль-структурной функции 25 Ui:hT()(tp- I fp-t Sa tf Jt - jl-atldi j , P eP л О о силу того, что рассматривается положительная полуось, где t J 0. Таким образом LU (г) laj-S. Среднее значение вьфа сения (20) оп деляется так л iu, (21) ( Определим в данном случае коэффициент стационарности аТр - ialo TU где То - длительность реализации процесса; сц - конечный сдвиг дискретизации процесса. Если принять, что обычно tuiO,1 Тр, то для коэффициента стационарности tL получим значение 5,77. 0,1 ТоЧ Таким образом, имеем резкое отличие коэффициента стационарности нестационарного по математическому ожиданию процесса от стационарных процессов. Предлагаемое устройство позволяет относительно просто и довольно точно различать стационарные и нестационарные процессы, что позволит повыситькачество анализа случайных процессов в любых областях научно-технической и производственной деятельности. Предлагаемое устройство обладает, прежде всего, повышенной достоверностью и точностыо определения нестационарности (стационарности) случайного процесса, а принципиальная схема гораздо проще по сравнению с известными устройствами того же назначения, благодаря простой логике вычисления коэффициента стационарности. Экономический эффект может быть получен при использовании данного устройства в АСУТП и в системах технической диагностики технологических процессов и технологического рборудования.
4tH«



| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО СТАБИЛИЗАЦИИ УРОВНЯ ЛОЖНЫХ ТРЕВОГ ПОМЕХОЗАЩИЩЕННОГО РАДИОЛОКАЦИОННОГО ПРИЕМНИКА, РАСПОЛОЖЕННОГО НА ВОЗДУШНЫХ НОСИТЕЛЯХ | 1990 |
|
SU1840162A1 |
| Устройство для определения характеристик случайных процессов | 1986 |
|
SU1310856A2 |
| Устройство для контроля достоверности информации | 1980 |
|
SU898488A1 |
| Устройство для измерения среднеквадратического значения шума | 1986 |
|
SU1425477A1 |
| Устройство для определения вероятностных характеристик случайного процесса | 1981 |
|
SU1013949A1 |
| Устройство для измерения средней скорости изменения частоты и линейности модуляционных характеристик частотно-модулированных генераторов | 1991 |
|
SU1781632A1 |
| Способ измерения отношения сигнал/шум | 1979 |
|
SU824068A1 |
| Устройство управления испытаниями на двухкомпанентные случайные вибрации | 1982 |
|
SU1093934A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СЛУЧАЙНОГОПРОЦЕССА | 1972 |
|
SU333569A1 |
| АДАПТИВНЫЙ ИЗМЕРИТЕЛЬ ПАРАМЕТРОВ НЕПРЕРЫВНЫХ ШИРОКОПОЛОСНЫХ СИГНАЛОВ | 2007 |
|
RU2349923C1 |
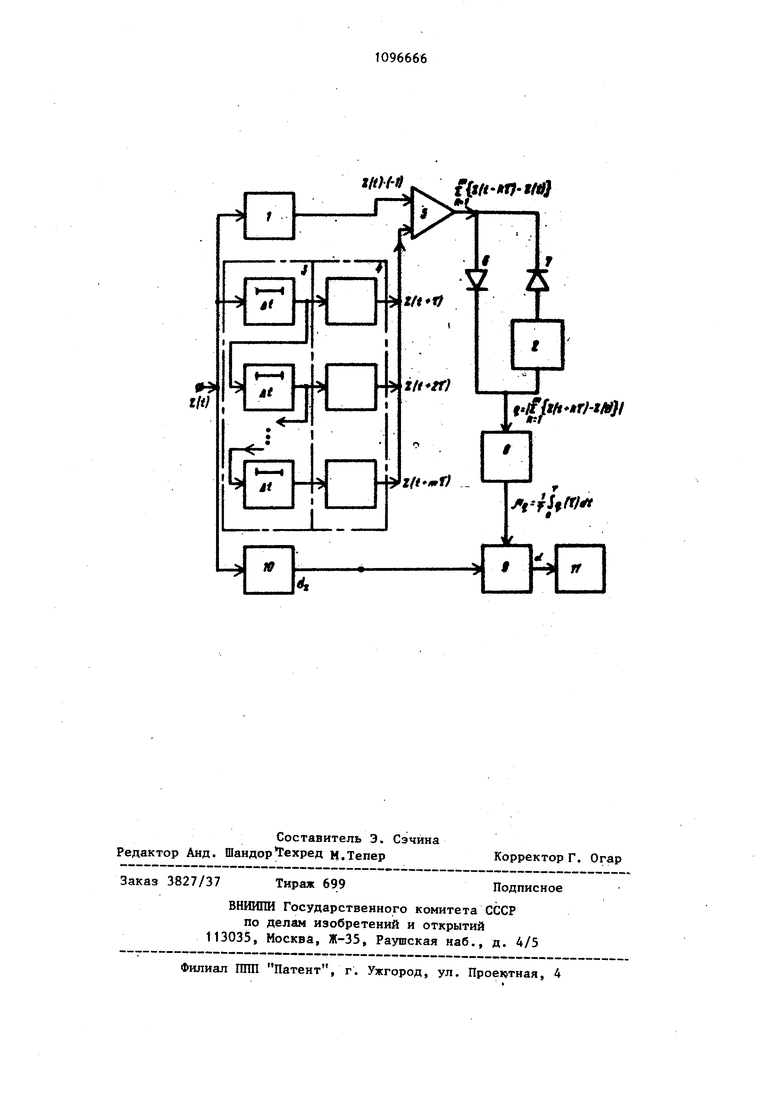
УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОСТИ СЛУЧАЙНОГО ПРОЦЕССА, содержащее блок определения разности и блок регистрации, отличающееся тем, что, с целью повьшения точности, оно содержит первый и второй фазовращатели, первый и второй детекторы, фильтр нижних частот, делителЕс напряжения, группу согласуюK ifcrfi.,; щих элементов, например катодных повторителей, блок определения среднеквадратичного отклонения и группу из последовательно соединенных элементов задержки, вход первого из которых объединен с входами первого фазовращателя, блока определения среднеквадратичного отклонения и является входом устройства, а выход каждо-го элемента задержки через соответствующий согласующий элемент подключен к первому входу блока определения разности, второй вход которого соединен с выходом первого фазовращателя, а выход блока определения разности через первьш детектор и через последовательно соединенные второй (Л детектор и второй фазовращатель лодключен к входу фильтра нижних частот, выход которого соединен с первым входом делителя напряжения, второй вход которого подключен к выходу блока определения среднеквадратичного отклонения, а выход делителя напряжения соединен с входом блока регистоаиии. а 9) а а
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА | 1972 |
|
SU453699A1 |
| кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| кл | |||
| (прототип). | |||
Авторы
Даты
1984-06-07—Публикация
1982-08-18—Подача