Для электротехнических расчетов применяются или общепринятые, или специальные типы логарифмических линеек. На специальных линейках можно выполнять некоторые дополнительные расчеты, интересующие электриков: подсчет коэффициентов полезного действия генераторов и двигателей, подсчет потерь напряжения в сетях, определение дробных степеней чисел, определение натуральных логарифмов и др.
Но необходимость в таких расчетах встречается сравнительно редко, так что иногда даже забываются назначение и способы употребления соответствующих шкал.
Вместе с тем до сих пор не разработаны линейки, облегчающие выполнение действий, часто встречающихся в электротехнических и других расчетах. Так, например, до сих пор логарифмические линейки не пригодны для выполнения действий сложения и вычитания, для простого отыскания величин 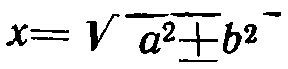 и величин
и величин 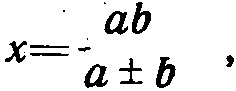 необходимых при расчетах токов коротких замыканий и других расчетов. Определение тригонометрических величин на линейках затруднено необходимостью применения движка, а часто и вычисления дополнительных углов. При существующих типах линеек трудно выполнить и действия с комплексными числами, имеющими существенное значение для выполнения самых разнообрзаных расчетов, связанных с электрическими цепями (расчеты линий передач, расчеты режимов систем, расчеты несимметричных режимов, расчеты цепей переменного тока и т.д.).
необходимых при расчетах токов коротких замыканий и других расчетов. Определение тригонометрических величин на линейках затруднено необходимостью применения движка, а часто и вычисления дополнительных углов. При существующих типах линеек трудно выполнить и действия с комплексными числами, имеющими существенное значение для выполнения самых разнообрзаных расчетов, связанных с электрическими цепями (расчеты линий передач, расчеты режимов систем, расчеты несимметричных режимов, расчеты цепей переменного тока и т.д.).
Расчеты с комплексными числами представляют значительную трудоемкость, что видно из того, например, что для умножения двух комплексов в алгебраической форме требуется выполнение шести элементарных действий, а деление таких же комплексов - одиннадцати действий.
Предлагаемая линейка не лишена ни одной из расчетных возможностей обычных линеек существующего типа и в то же время располагает рядом новых расчетных возможностей.
Расширение области расчетов, производимых посредством линейки, достигается тем, что она снабжена подвижной прозрачной пластинкой с растром из параллельных линий. Кроме того, на один из бегунков линейки нанесены функциональные кривые, точки пересечения которых с функциональными линиями корпуса переносятся вертикальными линиями растра на соответствующие шкалы.
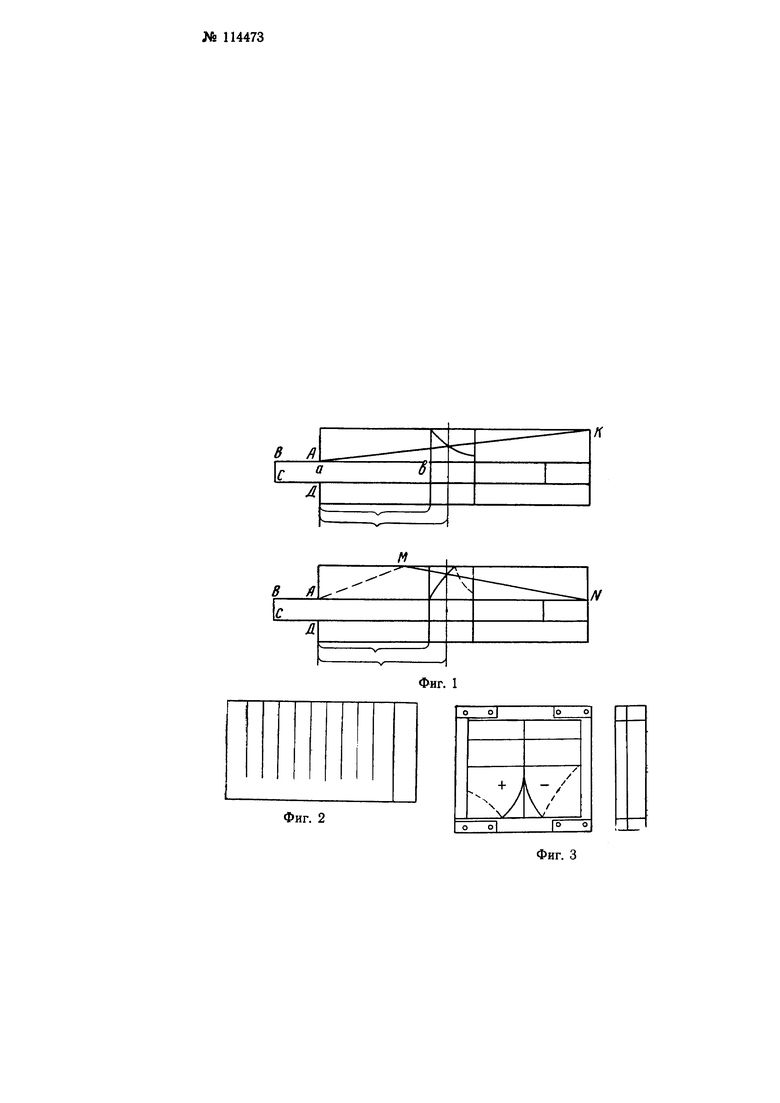
На фиг. 1 схематически изображены функциональные линии, нанесенные на корпус и бегунок; на фиг. 2 - прозрачная пластинка с растром; на фиг. 3 - основной и дополнительный бегунки; на фиг. 4 - корпус линейки.
Как известно, преобразование 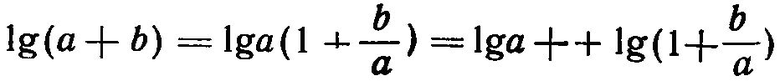 может быть использовано для выполнения сложения на логарифмической линейке. Применяя обычное обозначение четырех шкал линейки, начиная сверху, через А, В, С и Д (фиг. 1 и 2) можно для сложения чисел а и b поступить следующим образом:
может быть использовано для выполнения сложения на логарифмической линейке. Применяя обычное обозначение четырех шкал линейки, начиная сверху, через А, В, С и Д (фиг. 1 и 2) можно для сложения чисел а и b поступить следующим образом:
меньшее из чисел а, взятое на шкале С, устанавливают против левого или правого конца шкалы Д (правый конец шкалы Д используют в тех случаях, когда меньшее из чисел на шкале С находится правее большего). При этом большее число b, также взятое на шкале С, отметит на шкале Д разность отрезков чисел а и b, т.е., учитывая логарифмический характер шкал, число b/a.
Прибавляя к отношению b/a единицу, получают величину 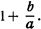 Фиксируя эту величину волоском бегунка на шкале Д и найдя соответствующее ей число на шкале С, получают сумму a и b, так как новый отрезок на шкале С, отсчитанный от начала, представляет собой сумму отрезков lga - на шкале С и
Фиксируя эту величину волоском бегунка на шкале Д и найдя соответствующее ей число на шкале С, получают сумму a и b, так как новый отрезок на шкале С, отсчитанный от начала, представляет собой сумму отрезков lga - на шкале С и 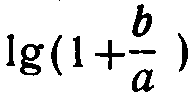 - на шкале Д.
- на шкале Д.
Так, например, если требуется сложить 30 и 40, то число 30 на шкале С устанавливают против левого конца шкалы Д. Против числа 40 на шкале С находят на шкале Д - 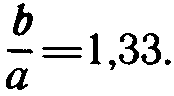 Следовательно,
Следовательно, 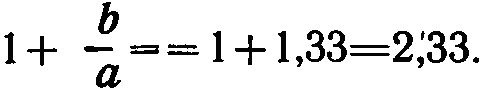 Против числа 2,33 на шкале Д находят на шкале С число 70, являющееся суммой 30+40. Очевидно, что если повторять ту же последовательность действий, то, пользуясь шкалой А вместо шкалы Д, можно получить не сумму 30+40, а
Против числа 2,33 на шкале Д находят на шкале С число 70, являющееся суммой 30+40. Очевидно, что если повторять ту же последовательность действий, то, пользуясь шкалой А вместо шкалы Д, можно получить не сумму 30+40, а 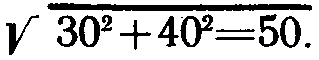 Это обстоятельство может быть непосредственно использовано для определения модуля комплекса, заданного в алгебраической форме. Аналогичные соображения и действия распространяют также и на выполнение действия вычитания. В этом случае,
Это обстоятельство может быть непосредственно использовано для определения модуля комплекса, заданного в алгебраической форме. Аналогичные соображения и действия распространяют также и на выполнение действия вычитания. В этом случае, 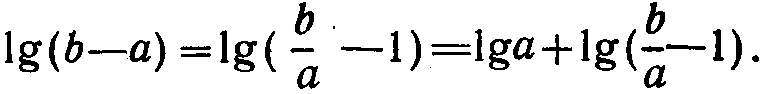 В предложенной линейке операции прибавления к lga величин
В предложенной линейке операции прибавления к lga величин 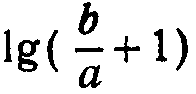 и
и 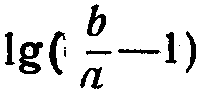 автоматизированы, в связи с чем нахождение промежуточных результатов и прибавление или вычитание из них единицы становятся ненужными. Кроме того, действия сложения и вычитания вместо шкал С и Д переносятся на шкалы А и Б, благодаря чему упрощается правило знаков, а также сложение и вычитание чисел, отношения между которыми могут доходить до 100.
автоматизированы, в связи с чем нахождение промежуточных результатов и прибавление или вычитание из них единицы становятся ненужными. Кроме того, действия сложения и вычитания вместо шкал С и Д переносятся на шкалы А и Б, благодаря чему упрощается правило знаков, а также сложение и вычитание чисел, отношения между которыми могут доходить до 100.
Упомянутая автоматизация получения результата достигается следующим образом.
Допустим, что на верхней части линейки нанесена прямая линия AK (фиг. 1) и что число а, взятое на шкале В, установлено против левого конца шкалы А. Фиксируют левым краем прозрачного бегунка число b на шкале В. На шкале А против числа b находится число 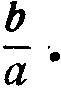 Находят вертикаль
Находят вертикаль 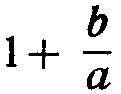 на шкале A и в месте пересечения этой вертикали с линией AK отмечают на бегунке точку. Очевидно, что для получения по точкам требуемой кривой на бегунке нет необходимости пользоваться движком. Установив левый край бегунка на любое число n на шкале А, отмечают на бегунке точку в месте пересечения линии AK и вертикали, проходящей через число n+1 на шкале А. Так, например, если левый край бегунка установить против числа 3 на шкале А, то точку на линии AK нужно отметить против числа 3+1=4 на шкале А. Полученная, подобным образом, кривая на бегунке в дальнейшем будет давать точку пересечения кривой бегунка с линией AK на вертикали, смещенной на
на шкале A и в месте пересечения этой вертикали с линией AK отмечают на бегунке точку. Очевидно, что для получения по точкам требуемой кривой на бегунке нет необходимости пользоваться движком. Установив левый край бегунка на любое число n на шкале А, отмечают на бегунке точку в месте пересечения линии AK и вертикали, проходящей через число n+1 на шкале А. Так, например, если левый край бегунка установить против числа 3 на шкале А, то точку на линии AK нужно отметить против числа 3+1=4 на шкале А. Полученная, подобным образом, кривая на бегунке в дальнейшем будет давать точку пересечения кривой бегунка с линией AK на вертикали, смещенной на 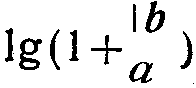 от левого края бегунка.
от левого края бегунка.
Аналогичным образом может быть построена кривая, соответствующая 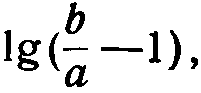 необходимая для выполнения вычитания. Однако, при недостаточно широкой верхней части линейки, полученная кривая в начале шкалы А пересекается под относительно острым углом с прямой AK. Для устранения этого недостатка, вместо прямой линии AK берется ломанная линия AMN (фиг. 1) с соответствующими двумя кривыми линиями на бегунке.
необходимая для выполнения вычитания. Однако, при недостаточно широкой верхней части линейки, полученная кривая в начале шкалы А пересекается под относительно острым углом с прямой AK. Для устранения этого недостатка, вместо прямой линии AK берется ломанная линия AMN (фиг. 1) с соответствующими двумя кривыми линиями на бегунке.
Для того, чтобы учитывать пересечение соответствующих одна другой ветвей прямых и кривых линий, они могут быть выполнены разного цвета или как сплошные или пунктирные линии.
Перенос точек пересечения функциональных линий на необходимую шкалу осуществляется посредством растра (фиг. 2), выполненного в виде прозрачной пластинки с нанесенными на нее вертикальными параллельными линиями. Растр перемещается независимо от бегунка до тех пор, пока ближайшая из вертикальных линий растра не попадет на точку пересечения вертикальных линий. В соответствии с этим, на корпус (фиг. 4) линейки наносятся две прямых линии, а на бегунок (фиг. 3) - четыре кривых линии.
Две левые кривые на бегунке служат для выполнения действий, связанных с вычитанием x=(b-a), 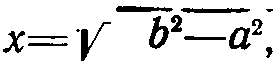
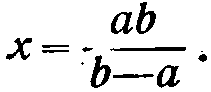 Две правые кривые на бегунке предназначены для выполнения действий, связанных со сложением x=(b+a),
Две правые кривые на бегунке предназначены для выполнения действий, связанных со сложением x=(b+a), 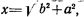
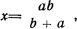 а также для преобразования комплексов из одной формы в другую.
а также для преобразования комплексов из одной формы в другую.
Для выполнения сложения пользуются шкалой Ш15 (фиг. 4). Меньшее из заданных слагаемых на шкале Ш15 устанавливают против левого (или правого) конца шкалы Ш14, а вертикальную линию бегунка устанавливают против большего из слагаемых на шкале Ш15. При этом искомая сумма может быть найдена на вертикали, проходящей через точку пересечения функциональных линий линейки и бегунка, также на шкале Ш15.
Отношение между слагаемыми при выполнении сложения может доходить до 100. Если это отношение больше 100, то сумму можно принять равной большему из слагаемых, причем погрешность при этом не превысит одного процента.
Если известны сумма и меньшее из слагаемых, а требуется найти большее из слагаемых, смещают движок до тех пор, пока меньшее из слагаемых на шкале Ш15 не установится под левым концом шкалы Ш14, а бегунок смещают до тех пор, пока его средняя вертикальная линия не установится против суммы на шкале Ш15. Далее, пользуясь левыми кривыми бегунка и растром, находят большее из слагаемых (также на шкале Ш15).
Эти действия сохраняются и для величин x=√b2+a2 и x=√b2-а2, при условии, что заданные величины будут прочитываться не на шкале В (Ш15), а на шкале С (Ш18). При этом, отношения между величинами b и a могут доходить до 10. При отношениях 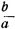 больших 10 x становится практически равным большему из чисел. Для часто требующегося при электротехнических расчетах определения величин
больших 10 x становится практически равным большему из чисел. Для часто требующегося при электротехнических расчетах определения величин 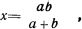 величины а, b и x устанавливают и находят на шкале Ш16 движка. При этом движок смещается до тех пор, пока большая из величин a и b не установится против левого конца шкалы Ш14. После этого среднюю вертикальную линию бегунка устанавливают против меньшей из заданных величин на шкале Ш16. Величина x может быть найдена на этой шкале на вертикали, проходящей через точку пересечения функциональных линий. Для контроля производимых вычислений необходимо иметь в виду, что результат должен получиться меньше меньшей из величин. На линейке при этих вычислениях можно находить x, если отношение между заданными величинами a и b не превосходит 100.
величины а, b и x устанавливают и находят на шкале Ш16 движка. При этом движок смещается до тех пор, пока большая из величин a и b не установится против левого конца шкалы Ш14. После этого среднюю вертикальную линию бегунка устанавливают против меньшей из заданных величин на шкале Ш16. Величина x может быть найдена на этой шкале на вертикали, проходящей через точку пересечения функциональных линий. Для контроля производимых вычислений необходимо иметь в виду, что результат должен получиться меньше меньшей из величин. На линейке при этих вычислениях можно находить x, если отношение между заданными величинами a и b не превосходит 100.
Если это отношение больше 100, то без большой погрешности величину x можно принять равной меньшей из заданных величин.
Для определения тригонометрических функций соответствующие шкалы Ш2-Ш13 перенесены на лицевую сторону линейки. Величины функций sinφ, cosφ и tgφ находят на шкале Ш1 или на шкале Ш19. Для шкал Ш6-Ш9 включительно значения шкалы Ш1 берутся в пределах от 0,1 до 0,01, а шкалы Ш19 - в пределах от 1 до 10.
Криволинейные стрелки, проставленные слева от тригонометрических шкал, показывают, в какую сторону углы нарастают, а вогнутостью - на какую из шкал Ш1 или Ш19 нужно ориентироваться. Из приведенных пояснений ясно также, как выполняется обратный переход от функций к углам.
На линейке можно находить также косинусы и котангенсы. Определение этих функций можно выполнять не только для первого, но и для остальных трех квадрантов, причем все необходимые определения выполняются без перемещения движка.
Для преобразования комплекса из алгебраической в показательную форму действуют также, как и при определении величины 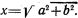 Так, например, имея комплекс a+jb=30+j40, устанавливают меньшее из чисел (30) на шкале Ш18 против левого конца шкалы Ш19.
Так, например, имея комплекс a+jb=30+j40, устанавливают меньшее из чисел (30) на шкале Ш18 против левого конца шкалы Ш19.
Правым концом шкалы Ш19 пользуются тогда, когда меньшее из чисел находится на шкале Ш18 правее большего, например, 40+j30.
Против большего числа (40) на шкале Ш18 устанавливают центральную вертикальную линию бегунка. Проектируя, посредством ближайшей линии растра, точку пересечения функциональных линий на шкалу Ш18, получают на этой шкале модуль 50. Заданные величины a и b и искомый модуль М всегда находятся на одной и той же шкале.
Для полноты преобразования комплекса кроме определения модуля требуется еще и определение угла. С этой целью шкалы на линейке размещены таким образом, что вертикальная линия бегунка, фиксирующая большую из составляющих комплекса, одновременно отмечает на шкалах Ш6-Ш13 и необходимый угол.
Таким образом, установив посредством движка и бегунка две входных величины (a и b) комплекса 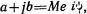 без промежуточных прочитываний и установок, получают обе выходные величины (М и φ). Следовательно, вместо шести и семи действий, требуемых для перевода комплекса из алгебраической формы в показательную, достаточно выполнения на линейке одного действия, примерно того же типа, что и обычное умножение, но с прочитыванием двух чисел вместо одного.
без промежуточных прочитываний и установок, получают обе выходные величины (М и φ). Следовательно, вместо шести и семи действий, требуемых для перевода комплекса из алгебраической формы в показательную, достаточно выполнения на линейке одного действия, примерно того же типа, что и обычное умножение, но с прочитыванием двух чисел вместо одного.
Для того, чтобы описанный способ преобразования комплекса распространить кроме первого также и на остальные три квадранта, тригонометрические шкалы маркированы углами в пределах от 0° до 180°. При этом принимается, что в показательной форме комплекс всегда будет иметь угол, не превосходящий 180°, так что вместо комплекса 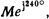 будет приниматься, например, комплекс
будет приниматься, например, комплекс 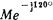
Для определения углов комплексов используются шкалы Ш6-Ш13. При этом, шкалы Ш10-Ш13 применяются тогда, когда отношения между составляющими комплексов находятся в пределах от 1 до 10, а шкалы Ш6-Ш10 - когда они находятся в пределах от 10 до 100. Во всех случаях, когда эти отношения больше 10, модули можно не определять и без большой погрешности принимать их равными большим из составляющих комплексов.
Таким образом, при преобразовании комплексов по соотношению величин a и b (от 1 до 10 или от 10 до 100) определяется необходимая группа шкал (tgT или sinT), а по соотношению вещественных и мнимых составляющих (a>b или b>a) и их знакам определяется необходимая шкала.
В случае необходимости выполнения обратного преобразования (Me±ja=±a±jb), вертикальная линия бегунка устанавливается на требуемый угол на шкалах Ш6-Ш13, одна из линий растра устанавливается на точку пересечения функциальных линий, а движок смещается до тех пор, пока модуль на шкале Ш18 не установится против выбранной линии растра.
При этом, на шкале Ш18 вертикальная линия бегунка и один из концов шкалы Ш19 отметят обе составляющие комплекса.
Это же преобразование можно выполнить также, установив модуль комплекса на шкале Ш17 против правого или левого конца шкалы Ш14 и фиксируя требуемые составляющие против величин sinφ и cosφ на шкалах Ш2-Ш5. Этим же приемом просто решается задача определения активной и реактивной мощностей по заданной кажущейся мощности (P=cosα; Q=sinα).
Так как вертикальная линия бегунка фиксирует на тригонометрических шкалах сразу несколько возможных углов, выбор требуемого угла выполняется на основании заданных знаков и по соотношению величин составляющих, и наоборот, пределы соотношения величин составляющих и их знаки определяются в зависимости от заданного угла. Необходимая ориентация облегчается восьмью типовыми примерами преобразования комплексов, приведенными в правом верхнем углу линейки.
Для облегчения умножения комплексов в алгебраической форме в линейке применен второй бегунок (фиг. 6). При умножении на шкале А двумя бегунками отмечаются составляющие одного из комплексов, например, при умножении комплексов (a+jb) (c+ja) числа c и d. Одно из этих чисел отмечается правым краем второго бегунка, а другое - левым краем растра. После этого движок смещается так, чтобы число a на шкале В установилось против левого конца шкалы А. При этом, два бегунка позволяют прочитать и записать два произведения: +ac и +jad. Затем движок смещается так, чтобы против левого конца шкалы А установилось число b на шкале В и прочитываются два новых произведения: -jbc и -bd. После этого в уме или посредством линейки выполняется сложение чисел j(ad+bc) и вычитание чисел (ac-bd).
Указанный способ умножения комплексов в алгебраической форме хотя и не дает сразу результат в окончательном виде, все же рационализирует действия по умножению комплексов, так как: устраняет лишние смещения бегунка и движка, упрощает определение места запятой в произведениях и уменьшает количество переходов от действий на линейке к записям на бумаге и наоборот.
Задняя сторона движка может быть использована для шкал, требующихся сравнительно редко: возведения величин в дробные степени, определения величины e-x определения гиперболических функций и т.д.
| название | год | авторы | номер документа |
|---|---|---|---|
| Вычислительное устройство | 1980 |
|
SU911544A1 |
| Счетная линейка | 1985 |
|
SU1275474A1 |
| Логарифмическая линейка для производства сложения и вычитания | 1932 |
|
SU28687A1 |
| Вычислительное устройство | 1985 |
|
SU1302301A1 |
| Счетная линейка | 1977 |
|
SU763907A1 |
| Логарифмическая линейка | 1983 |
|
SU1151992A1 |
| Счетная линейка | 1984 |
|
SU1231516A1 |
| СЧЕТНАЯ ЛИНЕЙКА ДЛЯ РАСЧЕТОВ ПРИ ТОКАРНЫХ, СВЕРЛИЛЬНЫХ, ФРЕЗЕРНЫХ, СТРОГАЛЬНЫХ И Т. П. РАБОТАХ НА МЕТАЛЛООБРАБАТЫВАЮЩИХ СТАНКАХ | 1944 |
|
SU69261A1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ УЛЬТРАЗВУКОВОГО КОНТРОЛЯ | 1991 |
|
RU2011223C1 |
| ЛОГАРИФМИЧЕСКИЙ СЧЕТНЫЙ ПРИБОР | 1935 |
|
SU47114A1 |

Логарифмическая счетная линейка, преимущественно для производства электротехнических расчетов, имеющая корпус и движок, снабженные шкалами и функциональными линиями, и два бегунка, отличающаяся тем, что, с целью расширения области производимых на линейке расчетов, она снабжена подвижной вдоль линейки прозрачной пластинкой с растром из параллельных линий, а на один из бегунков нанесены функциональные кривые, точки пересечения которых с функциональными линиями корпуса переносятся вертикалными линиями растра на соответствующие шкалы.
Авторы
Даты
1958-08-31—Публикация
1956-08-20—Подача