(54) ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО Изобретение относится к аналоговым; .механическим устройствам с ручным управлением, а более конкретно к устройствам, имеющим прямолинейные шкалы и отличающимся граду1фовкой шкал, и может использоваться в практике вычислений в тех случаях, когда требуется вы числять суммы и разности квадратов ряда числе, квадраты и квадратные корни. Известны вычислительные устройства, содержащие корпус, в пазах которого расположены движок и бегунок. Из-за того, что сложения (вычитания входят в качестве гфомежуточных дей; ствий в выражениях, например, вида Уа - -а|;ц-...-Юи . при использовании такого устройства 1 ибегают для каждого сложения к приему сложения с единицей. Каждое из сложений требует одной установки движка и двух установок бегунка со считыванием значений и промеж точным мысленным прибавлением единицы. Соответственно, для нахождения сум МЫ квадратов Y чисел (или квагфатного корня из такой суммы) требуется (Vj ) установка движка и 2 (и-1) установок бегунка и считываний меток, ьозраствет возможность ошибок от вещ}аввпьдых и неточных установок подвижных элементов, значительно возрастают напряжение раочетчика и длительность вычисления. Поэтому приходится прибегать к записи промежуточных результатов с их слож&нием вручную или же к попутному иопользованию ари }мометра. Первое не сокращает ительность вычислений, а второе не удешевляет используемые щзн вычислении средства. Наиболее близким техническим решением к щэедпагаемому является вычисли тельное устройство, содержащее первую и вторую шарнирно скрепленные одними концами линейки, на которые нанесены равномерные шкалы, на каждой из линеек размещен бегунок с визиром, и третью линейку, снабженную продольной пробегунрезью и подвижно сопряженную с нами первой и второй линеекГ2. Недостаток известного устройства ограниченный класс решаемых...задач. Цель изобретения -расширение класса решаемых задач и повышение точноети. Поставленная цель достигается тем, что в вычислительном устройстве третья линейка снабжена подвижным . фиксатором выполненным в виде подпружиненного штифта, расположенного в прорези третьей линейки, бегунок каждой линейки снабжен ребром, расположенным перпендикулярно продольной оси этой линейки И выемкой на одном из торцев, ребро бе гунка одной линейки размешено в прорези третьей линейки, в подпружиненный штифт помешен в выемке бегунка другой линейки, на третьей линейке нанесена равномерная шкала, а на первой и второ линейках квадратичные шкалы. На фиг. 1 представлено вычислительное устройство при первом сложении или при вычитаниях квадратов величин; на фиг. 2 - то же, при последуюших сложениях квадратов величин. Вычислительное устройство содержит три линейки 1 - 3, из которых линейки 1 и 2 соединены концами посредством плоского шарнира 4. Линейки 1 р 2 кон структивно одинаковы и несут каждая по перемещаемому по их длине бегунку 5 или 6. Бегунки могут быть выполнены подпружиненными относительно своих линеек или же иметь фиксаторы. Каждый КЗ бегунков выполняет двойную функцию, обеспечивает направление линейки 3 под прямым углом к данной и служит для считывания меток со шкал. Для направления линейки 3 под прямым углом бегунки имеют ребро 7, входящее в продольную прорезь 8 линейки 3 и перпендикулярное продольной оси той линейки, на которой установлен бегунок. Для уста новки и считывания меток со шкал линее каждый бегунок имеет визир 9. Кроме того, каждый бегунок имеет круглую выемку 10, используемую для сопряжения с фиксатором 11, выполненным в вине подпружиненного штифта, который установлен в прорези 8 линейки 3 с возможностью перемещения по ней. Линейка 3 с фиксатором 11 расположена по высоте между линейками 1 и 2 и не препятствунт их переводу одна за другую. Ре& ра 7 бегунков выполнены на одном бегу ке с верхней, а на другом с нижней сто роны планки. 9 4 Линейки 1 и 2 несут на своих одинаковых по ходу вращения кромках (верхних) одинаковые равномерные шкалы 12 и 13, имеюш:ие своим началом ось шарнира 4, а линейка 3 имеет такую же равномерную шкалу 14, нанесенную вдоль прорези 8. Со шкалами 12 и 13 сопряжены неравномерные - квадратичньге шкалы 15 и 16, нанесенные на противоположньгх кромках линеек. Все шкалы 12-16 начинаются с нулевых делений, Величине, устанавливаемой визиром 9 бегунка по метке шкалы 12 (13), отвечает квадрат этой величины на шкале 15 (16). На устройстве вычисляют следующие выражения: суммы квадратов: где И-целое, любое конечное число; разности квадратов: ... 2, /1. , л L12. м-Я,-V 171 и целое,суммы или разности квадратов с наличием невозведенных в квадрат чисел - слагаемых и (или) вычитаемых: ... + 4 Ь-г-Ь|- ...,-f-P2+ ... -bPv,-9c, -96, где к, t - целые Р.- любые действительные числа; квадратные корни сумм и разностей и любых других чисел; ...-ка;-Ъ ь;-...-Ь%Р,.Р....,,,-.,.-(Уе; кратные двум степени чисел и кратные двум корни из чисел. Вычисления на устройстве осуществляются следующим образом. При нахождении суммы квадратов (фиг. 1) бегунок 5 на линейке 1 ставят визиром 9 на деление А ее равномерной шкалы 12. Линейку 3 пропускают прорезью 8 в ребро 7 бегунка и устанавливают на деление А,2 шкалы 14. Нажатием фиксатора 11 фиксируют линейку 3 ее концом на кромке линейки 3. Бегунок 6 подводят выемкой 10 под фиксатор 11. Далее линейку 1 освобождают (отгибая) от сопряжения с линейкой 3 и переводят за линейку 2 (против хода часовой стрелки, фиг. 2), Отлсав фиксатор 11, разворачивают линейку 3 до соы«1ещения ее прорези 8 с ребром 7 бегунка 6 и подают ее вдоль бегунка (или вытягивают) на деление АЗ шкалы 14. Переместив фиксатор 11 в начало шкалы 14 линейки 3, фиксируют последнюю на кромке лийейки 1, подводят бегунок 5 выемкой 10 под фиксатор 11. Далее повторяют действия с линейкой 3, освобождая ее от бегунка 6, разворачивая вводят прорезью 8 в ребро 7 бегунка 5, подавая на деление А4 Цйсалы 14 и фиксируя началом на 5& кромке линейки 2, переведенной за линейку 1. Действия повторяются с поочередны.- ми переводами линеек 2 и 1, имитирующим увеличивающиеся по длине гипотенузы прямоугольных треугольников, до задания линейкой 3 последнего - А. Каждая из гипотенуз, соответствующая некоторой сумме квадратов, становится при следующем механическом вычислении (перемещением линейки 3) катетом. Поскольку метки щкал 15 и 16 являются квадратам.и значений соответствующих сопряженных с ними равномерных щкал 12 и 13, квадрат полученной таким образом последней гипотенузы считыва . ют по визиру 0 бегунка, со шкалы 15 или 16. При вычислении разностей квадратов (фиг. 1) перемещения линейки 3 осуществляют в обратном направлении, имитируя переводимыми линейками 1 и 2 катеты прямоугольных треугольников. При выведенном из прорези 8 ребре 7, напр№мер бегунка 6, оставив фиксацию линейки 3 на кромке линейки 2, устанавливают линейку 3 делением В, на линейку. 1. Фиксируют прямой угол бегунком 5, введя его ребром 7 в прорезь 8 линейки 3. Отжав фиксатор 11, переводят линейку 2 (по часовой стрелке) за линейку 1. Расфиксировав линейку 3, вводят ее концгал на кромку линейки 1, фиксируют, делением В устанавливают на линейку 2, фиксируют прямой угол бегунком 6 и т. д. Если среды суммы или разности квадратов имеются невозведенные в квадрат слагаемые P-i или вычитаемые , то для каждого р (Q-j) предварительно ставят один из бегунков 5 или 6 на деление () шкалы 15 Ш1И 16 и считывают на шкалах 12 или 13 квадратный корень этой величины - ( ). С полученными значениями поступают описанным ранее образом, устанавливая.линейку 3 делением-( 1/оГЛ ее шкалы 14. При определении квадратных корней из сумм или разностей квадратов необходимость обращения к неравномерным .шкалам 15 и 16 отпадает, достаточно прочесть конечный результат на равномерной шкале 12 или 13. Вычисление 4.6 квадратов, квадратных корней, а также кратных двум степеней и корней чисел осуществляется бегунками 5 и 6 ва линейках 1 и 2 подобно вычислениям на обычной счетной линейке и специальных .пояснений не требует. Для сумм, разностей квадратов и квадратных корней из сумм разностей исключается считывание всех промежуточных результатов, а установка значений ведется только по одной равнойерной щкале 14, естественно, более точной, чем неравнсмерные шкалы (как известно, равномерные шкалы по своей точности не уступают точности аналитических методов технических расчетов). Поэтому возможность ошибок от неправильного считывания меток и от неправильной установки подвижных элементов сведена к минимуму, соответственно уменьшается и напряжение расчетчика, Фор.мула изобретения Вычислительное устройство, содержа,щее первую и вторую шарнирно скреплееные одними концами линейки, на которые нанесены равномерные шкалы, на каждой из линеек размещен бегунок с визиром, и третью линейку, снабженную продольной прорезью и подвижно сопряженную с бегунками первой и второй линеек, о г личающееся тем, что, с целью расширения класса решаемых задач и повышения точности, третья линейка снаб подвижным фиксатором, выполне ным в виде подпружиненного штифта. расположенного в прорези третьей линей- . ки, бегунок каждой линейки снабжен ребром, расположенным перпендикулярно продольной оси этой линейки и выемкой на одном из торцев, ребро бегунка одной линейки размещено в прорези третьей линейки, а подпружиненный штифт помещен в выемке бегунка другой линейки, Р третьей линейке .нанесена равномерная шкала, а на первой и второй линейках квадратичные шкалы. Источники информации, принятые во внимание при экспертизе .1. Панов Д.Ю. Счетная линейка, М., Учпедгиз, 1978, с. 107-110. 2. Авторское свидетельство СССР № 653, кл. G06Q 1/04, 1923 (прототип).


| название | год | авторы | номер документа |
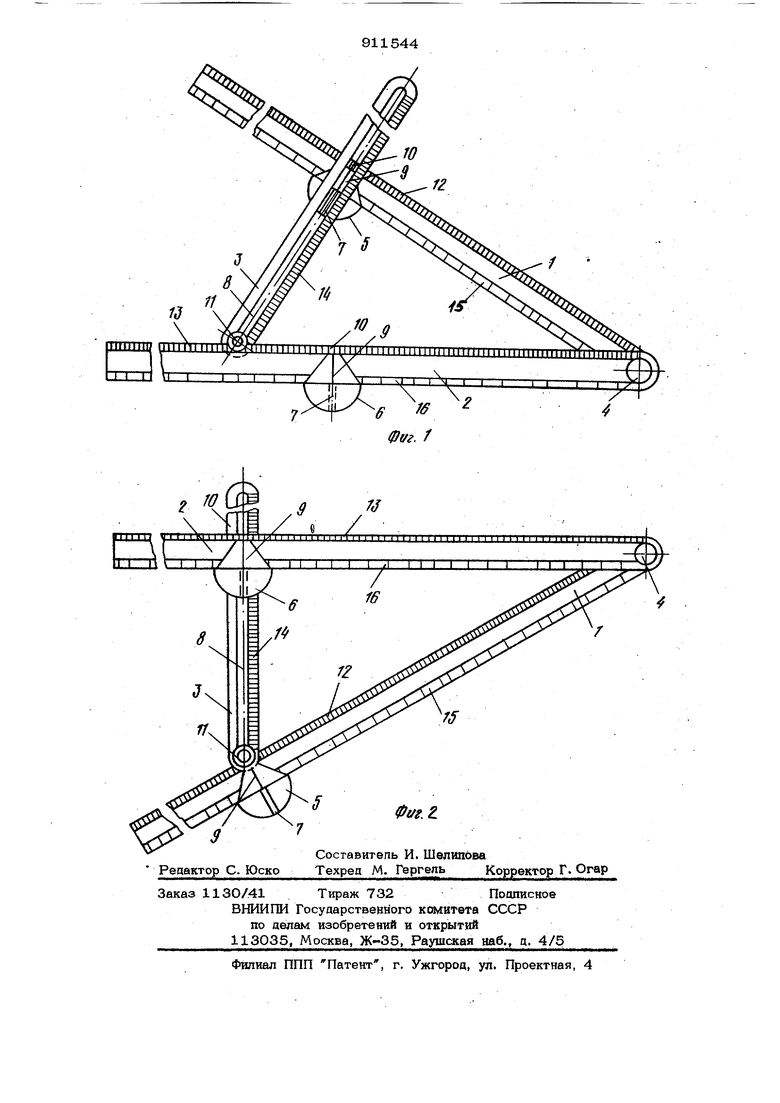
|---|---|---|---|
| Вычислительное устройство | 1985 |
|
SU1302301A1 |
| Логарифмическая счетная линейка | 1956 |
|
SU117763A1 |
| ЛОГАРИФМИЧЕСКАЯ СЧЕТНАЯ ЛИНЕЙКА | 1956 |
|
SU114473A1 |
| Счетная линейка | 1977 |
|
SU763907A1 |
| Прибор для построения аксонометрических проекций объекта | 1972 |
|
SU449830A1 |
| СЧЕТНОЕ УСТРОЙСТВО | 1946 |
|
SU70052A1 |
| Логарифмическая линейка для производства сложения и вычитания | 1932 |
|
SU28687A1 |
| Линейка для расчета шихты сталеплавильных печей | 1957 |
|
SU117445A1 |
| Прибор для расчета электрических цепей | 1981 |
|
SU993276A1 |
| Вычислительный прибор | 1983 |
|
SU1105900A1 |


Авторы
Даты
1982-03-07—Публикация
1980-03-28—Подача