/
Itaek
СО СО
фь
S

| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения термоокислительной стабильности низкомолекулярных нефтепродуктов | 1983 |
|
SU1187054A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗАТУХАНИЯ ПЕРЕМЕННОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В КОСМИЧЕСКОМ ПРОСТРАНСТВЕ | 2013 |
|
RU2537084C1 |
| Устройство для имитации тангенса угла потерь | 1986 |
|
SU1468208A1 |
| Способ контроля диэлектрических свойств жидкого диэлектрика маслонаполненных высоковольтных аппаратов | 1987 |
|
SU1506386A1 |
| Способ определения параметров диэлектрических материалов | 1988 |
|
SU1642411A1 |
| Преобразователь теплоты в энергию переменного электрического тока | 2017 |
|
RU2664676C1 |
| Устройство для измерения параметров конденсаторов | 1980 |
|
SU905878A1 |
| МОСТ С ИНДУКТИВНО СВЯЗАННЫМИ ПЛЕЧАМИ ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ КОНДЕНСАТОРОВ | 1969 |
|
SU250299A1 |
| Эталон единицы тангенса угла потерь | 1982 |
|
SU1107656A1 |
| Способ исключения погрешности, вызываемой сильными внешними электромагнитными и электростатическими полями, при измерении угла диэлектрических потерь изоляции высоковольтной аппаратуры | 1954 |
|
SU103486A1 |

Изобретение относится к электрическим измерителям и может быть использовано для определения бесконтактным способом электрического сопротивления тонких проводящих слоев раз- личных веществ, находящихся либо в свободном состоянии, либо в виде пле нок или покрытий на непроводящем основании. Изобретение повышает точность определения сопротивления проводящего слоя. Устройство, реализующее предложенный способ, содержит две пластины 1 и 2 плоского конденсатора, между которыми размещен тонкий измеряемый проводядий слой, расположенный под углом q по отношению к пластинан чк которым подключен прибор для измерения емкости с конденсатора и тангенса угла потерь tg S .По дайденным значениям этих величин выполняют ряд математических преобразований и расчетов, приведенных в описании изобретения, и по выведенной формуле определяют величину сопротивления тонкого проводящего слоя. 2 ил. (Л
е/г, /
Изобретение относится к электрическим измерениям и может быть использовано для определения бесконтактным методом электрического сопротивления тонких проводящих слоев различных веществ, находящихся либо в свободном состоянии, либо в виде пленок или покрытий на непроводящем осно.вании.
Целью изобретения является новы- ю шение точности определения сопротивления тонкого проводящего слоя.
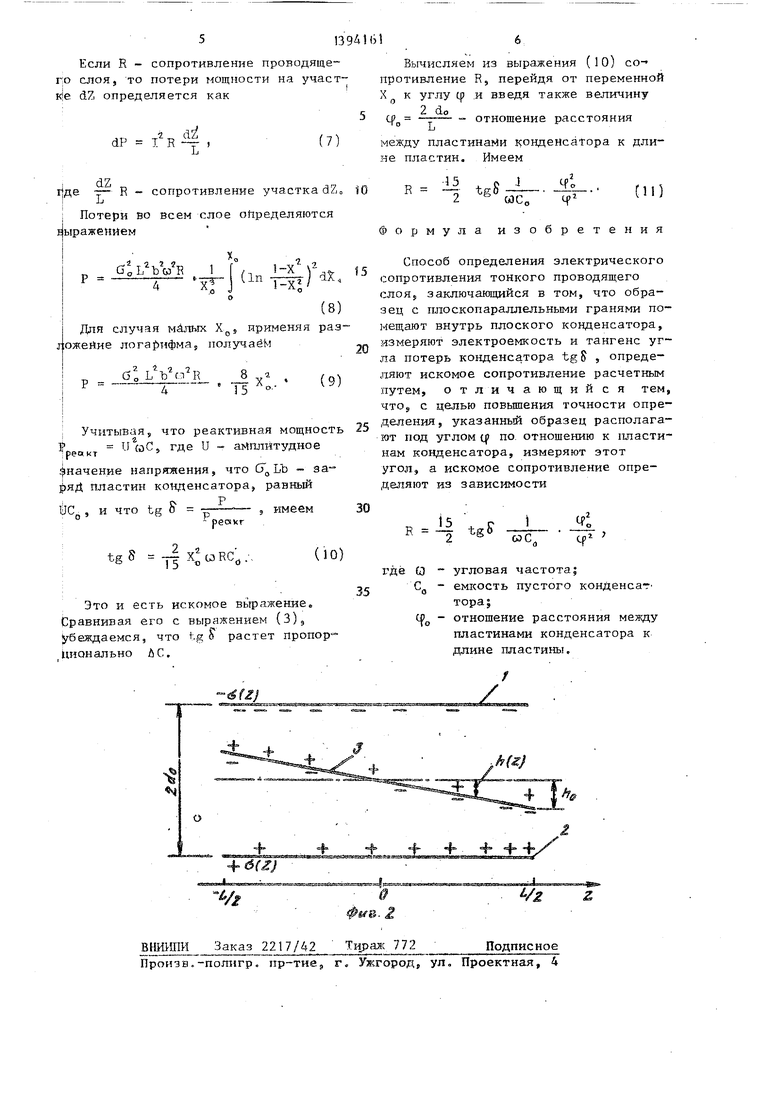
На фиг. 1 приведена структурная схема устройства для измерения сопро- тивления тонкого проводящего слоя; 15 на фиг, 2 - схема расположения зарядов в измеряемом слое и на пластинах конденсатора.
Устройство (фиг. 1) содержит две пластины плоского конденсатора верх- 20 нюю и нижнюю 2, размещенный между ними измеряемый тонкий проводящий слой 3 (его толщина не показана), расположенньп по отношению к пластинам конденсатора под некоторым углом 25 ср, подключенный к пластинам конденсатора прибор 4 (например, мост переменного тока) для измерения емкости С и тангенса угла потерь tgS. / 30
Способ осуществляется следующим
образом.
Измеряемый тонкий проводящий слой 3 располагается конденсатора под некоторым углом ср по отношению к его пластинам 1 и 2.
С помощью прибора 4 измеряются С, tgS и по найденным значениям этих величин расчетным путем определяется продольное сопротивление проводящего Q слоя 3.
Для выяснения вопроса о связи измеренных величин С, tgS с сопротивлением проводящего слоя и углом его наклона рассмотрим теоретически со.от- дс ветствующую задачу.
Пусть имеется плоский заряженньш конденсаторV(фиг. 2), внутри которого располагается под некоторым углом С| проводящий слой 3. Наличие внутри ,. слоя продольной составляющей вектора электрического поля конденсатора вызывает перераспределение зарядов в нем, кроме того, перераспределяются заряды и на пластинах конденсатора. Ясно, что этот эффект возрастает при увеличении угла qi , так как при этом возрастает продольная составляющая вектора электрического поля в слое.
Как показывают расчеты, происходит также изменение емкости конденсатора С.
Если к конденсатору подключить переменное напряжение, то внутри сло возникает переменный электрический ток, который ведет к потерям электрической мощности на сопротивлении R слоя. Вследствие этого конденсатор для подключенного к нему генератора переменного напряжения представляет собой нагрузку, имеющую не только емкостную составляющую, но также и активную. Обычно потери электрической мощности в конденсаторе выражаются tgo , который определяется как отнощение активной составляющей полного сопротивления к реактивной составляющей.
Получаем зависимость параметров конденсатора С, tgS от сопротивления R и угла наклона ср проводящего слоя 3. Считаем, что этот слой имеет такие же размеры, как и пластины 1 и 2 конденсатора, расположен внутри конденсатора симметрично по отношению к его пластинам и что размеры пластин конденсатора много боль- Eje расстояния 2 d,, так что можно синус и тангенс угла ср заменять им самим.
Вычисляем вначале емкость конденсатора в зависимости от наклона про- .водящего слоя 3 для случая постоянного тока (электростатика),
Проводящий слой делит плоский конденсатор на два последовательно соединенньк неплоских конденсатора верхний и нижний, В электростатическом случае потенциал один и тот же для всех его точек. Поэтому для любого из двух образовавщихся конденсаторов напряженность элекрического поля обратно пропорциональна расстоянию между пластинами. То же самое можно сказать о поверхностной плотнсти зарядов С , которая является Функцией переменной Z.
На проводящем слое с нижней сторны плотность зарядов такая же, как на нижней пластине 2 конденсатора, а с верхней стороны - как на верхне пластине 1, Суммарная плотность зарядов в слое определяется суммой этих двух величин. Видно, что левая сторона -СЛОЯ заряжена положительно, а правая - отрицательно.
31394;
Для нижней пластины 2 конденсатора имеем
СГ 5„
do-h
h
Cf-
Z - текущая координата;
GQ - поверхностная плотность за- ю ряда в центре пластины 2 конденсатора;
(j - поверхностная плотность зарядов на пластинах конденсатора в отсутствие прово- 15 дящего слоя 3 (считаем, что напряжение на конденсаторе поддерживается постоянным). Проинтегрировав выражение для G
координате Z в пределах от - -г- - (L - длина пластины), получаем
общий заряд пластины конденсатора
Q б„ L b
In
1 + Хс 1 - Х„
где X i
b - ширина пластины.
Величина Х , также как и угол Cf , характеризует наклон слоя 3, Х изменяется от О до 1, в то время как угол if изменяется от О до своего мак симального значения.
Учитывая, что емкость пропорциональна заряду, получаем закон изменения емкости конденсатора
С С f(XJ, где f(Xo)
In
1 + Хс
1 - X,
откуда видно, что при малых Х f(X)- 1 изменяется пропорционально квадрату угла наклона слоя.
Рассмотрим теперь вопрос о потерях электрической мощности при подключе- НИИ конденсатора с пров.одящим слоем 3 к источнику переменного тока. Если электрическое поле в конденсаторе переменное, а слой имеет сопротивление, то заряды в нем не успевают пе- ретекать с одного края на другой в должной мере. Соответственно этому и на пластинах 1 и 2 конденсатора меньшее изменение заряда, вследствие
1394;
1)
ю
15
25
30
- ,с
40
45
- у
61
чего емкость конденсатора изменяется
слабее, чем в случае постоянного
тока.
Таким образом, при изменении сопротивления проводящего слоя 3 от нуля до бесконечности емкость конденсатора изменяется от значения С, вычисленного вьпде для постоянного тока, до значения С, свойственного конденсатору в отсутствие проводящего слоя 3.
Потери электрической мощности имеют иную, не монотонную зависимость ; Потери малы и при малом сопротивлении (нет сопротивления) и при очень большом (нет тока).
Так как решение задачи о потерях в общем виде затруднительно, рассмотрим лишь случай малого сопротивления проводящего слоя 3. Будем считать, что перетекание зарядов по пластине происходит в полной мере и справедливо полученное выше выражение для
6(z).
Вычислим заряд c|;(z), перетекающий в проводящем слое 3 в область, расположенную правее Z. Для этого нужно
взять интеграл от Z до - , учтя,
что в проводящем слое плотность заря-, да складывается из двух величин. Вследствие симметрии расположения слоя имеем
U2
q(Z) 1 -G (Z) +G(-Z) bdZ, (4)
Z
где C (Z) определяется выражением (1). Знак минус перёд С) (z) учитывает знак заряда.
Вычисление выражения (4)
г
q(Z) -С Lb -Ar- In
-О Lb о 2 Xo
1 - X
где X
Ь d.
(5)
Заряд q.(Z) не что иное, как заряд, проходящий через сечение слоя, имеющее координату Z. Дифференцируя эту величину по времени, получаем силу тока. Так как закон изменения по времени - гармонический с частотой О, имеем для амплитуды силы ток а
In
1 - X 1 - Х
(6)
Если R - сопротивление проводяще- Г1О слоя, то потери мощности на участие dZ определяется как
,р л Д аР I R ) Ij
(7)
dZ
R - сопротивление участка dZ iO
I Потери во всем слое определяются Е|ыражеяйем
1
о,
J1 V i2 (in ) d..
(8)
Для случая мАлых применяя раэ- ожейие логарифма, получает)
-- X
15 -
(9)
; Учитывая, что реактивная мощност еакт , где и - амплитудное
Значение напряжения, что G ЬЪ - за- яД пластин конденсатора, равный
Р
УС
и что
tg&
имеем
pecskr
tgS у|
(10)
Это и есть искомое выражение. Сравнивая его с выражением (3), убеждаемся, что tg Ь растет пропор иионально и С,
«
+
V/
вню-ши
Заказ 2217/42 THj)a3c 772
Произв.-полигр, пр-тие, г. Ужгород, ул„ Проектная, 4
Вычисляем из выражения (10) со- противление R, перейдя от переменной Х к углу ср я введя также величину
2 do jf - отношение расстояния
L
между пластинами конденсатора к длине пластин.
Имеем J
R. i| t.8
Ч с
Ч
11)
Формула изобретения
Способ определения электрического сопротивления тонкого проводящего слоя, заключающийся в том, что образец с плоскопараллельными гранями помещают внутрь плоского конденсатора, измеряют электроемкость и тангенс угла потерь конденсатора tg S , определяют искомое сопротивление расчетным путем, отличающийся тем, что, с целью повышения точности определения, указанньй образец располагают под углом q по отношению к пластинам конденсатора, измеряют этот угол, а искомое сопротивление определяют из зависимости
R
15
tg
we.
1
7F
где О угловая частота;
Сд емхсость пустого конденсаг
тора;
- отношение расстояния между пластинами конденсатора к длине пластины.
,
в
Vj
Z,
Подписное
| Берлинер М | |||
| А | |||
| Измерение влажности.- М.: Энергия, 1973, с | |||
| Приспособление в центрифугах для регулирования количества жидкости или газа, оставляемых в обрабатываемом в формах материале, в особенности при пробеливании рафинада | 0 |
|
SU74A1 |
Авторы
Даты
1988-05-07—Публикация
1986-05-28—Подача