Id
i
Г
/,
/У
СП
1C ю сд
4ib





| название | год | авторы | номер документа |
|---|---|---|---|
| Способ моделирования эволюции материи | 1989 |
|
SU1681322A1 |
| Способ моделирования эволюции квантовой системы и устройство для его осуществления | 1989 |
|
SU1776354A3 |
| ПАЗОННЫЙ СПОСОБ МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСКИХ МАШИН И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1998 |
|
RU2137286C1 |
| Пазонный способ моделирования физических полей | 1989 |
|
SU1804649A3 |
| Решающий блок аналогового процессора | 1988 |
|
SU1667114A1 |
| Способ преобразования сигналов | 1982 |
|
SU1216822A1 |
| ПАЗОННЫЙ СПОСОБ МОДЕЛИРОВАНИЯ ПЕРВИЧНЫХ ИСТОЧНИКОВ ЭНЕРГОСИСТЕМЫ С ЭНЕРГОНОСИТЕЛЯМИ РАЗЛИЧНОЙ ПРИРОДЫ | 2001 |
|
RU2224286C2 |
| Многофункциональное параметрическое устройство | 1981 |
|
SU1014149A1 |
| Устройство для передачи информации | 1986 |
|
SU1490722A1 |
| Фазометр | 1990 |
|
SU1737359A1 |


Изобретение относится к моделированию и радиофизике и может быть использовано для исследования физических полей в системах с различной формой движения материи (механической, электрической, магнитной, химической, биологической, тепловой и т.п.).Целью изобретения является расширение области применения устройства. Устройство выполнено в виде N параметрических систем 11-1N, каждая из которых два магнитных сердечника 2 и 3 с резонансными обмотками 4 и 5 и обмотками накачки 6 и 7, RC-фильтр, вход 10 задания напряжения накачки, блок моделирования активных потерь, выполненный в виде токозадающего резистора 11, резистор 12 задания тока накачки, информационный вход 13. Достижение поставленной цели обеспечено благодаря введению в устройство блока моделирования активных потерь, выполненного в виде токозадающего резистора и резистора задания тока накачки, а также новым связям между элементами устройства. 7 ил., 1 табл.
..J
I
,J
f
Изобретение относится к моделированию и радиофизике и может быть использовано для исследования физическ полей и явлений в системах с различной формой движения материи (механической, электрической, магнитной, химической, биологической, тепловой и т.п.),
Целью изобретения является расши- рение области применения устройства.
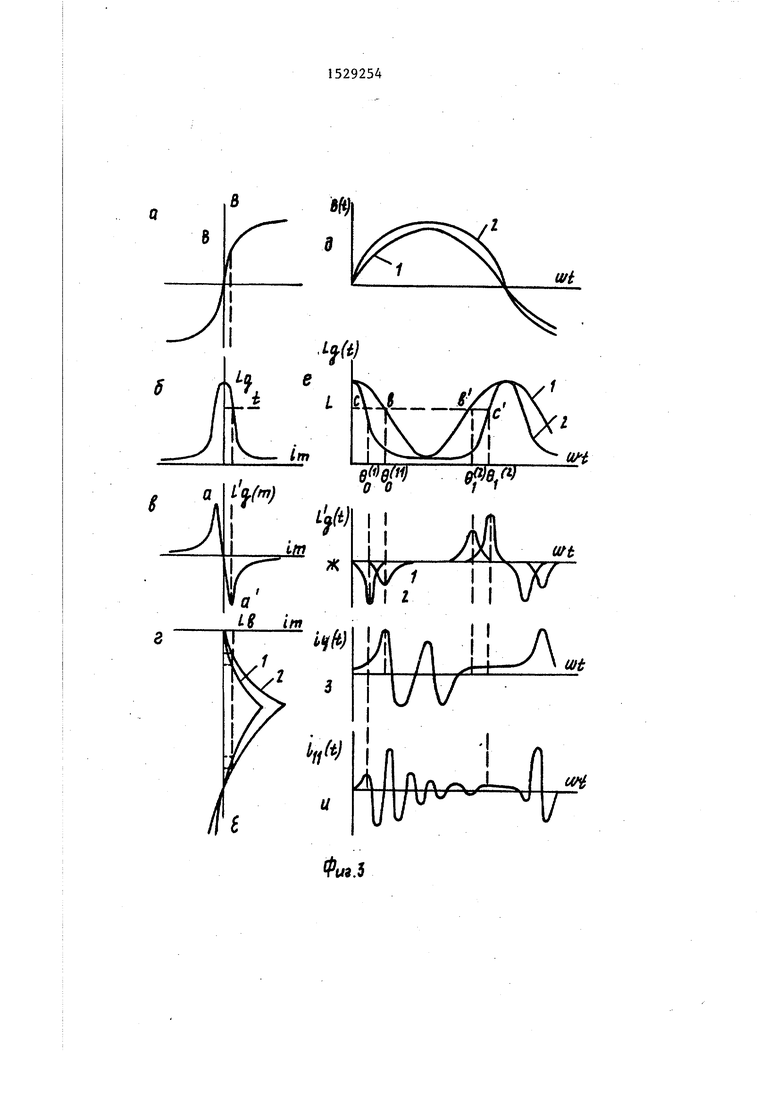
На фиг.1 приведена схема устройства; на фиг.2 - параметрический зонный (пазонный) принцип эволюции движения ; на фиг.З - частотные ха-, рактеристики пазонной системы; на фиг.А и 5 - механизм возбуждения па- зонных колебаний в пятой и девятой зонах неустойчивости; на фиг,6 и 7 - эпюры финитного движения в микросис- теме и макросистеме.
Устройство (фиг.1) выполнено в ви N распределенных пазонных систем (, где п 1, Z, 3... - номер зоны неустойчивости) , каждая из которых содержит два магнитных седечника 2 и 3 с резонансными обмотками 4 и 5 и обмотками накачки 6 и 7, RC-фильтр, состоящий из резистора 8 и конденсатора 9, вход 10 задания напряжения накачки, блок моделирования активных потерь, вьшолненный в виде токозадающего резистора 11, резистор 12 задания тока накачки, информационньш вход 13.
Устройство работает следующим образоМо
На входы 10 и 13 первой пазонной системы подается напряжение U(x, t) и ток i(x, t), зависящие от координа ты X и времени t. По обмоткам 6 и 7 накачки (W,), соединенным последова
зЧ
х
1 ЗЧ
I74t) at
CO
(t) ; (t) CGL + RC + CLj(t) ;
sw
(t) G(R + L (t)) + CL (t)); L L, --p
где LU(t) - мгновенная частота;
cP(t) - коэффициент демпфирования;(t) - коэффициент расстройки;
LO. Ь,
динамическая и геометрическая индуктивности;
0
О
Q
5
тельно и согласно, протекает ток -на- Качки i|, который модулирует индук- тивности обмоток сердечников 2 и 3 с удвоенной частотой о напряжения V(t) накачки. Резонансные обмотки 4 и 5 (W,) нелинейных индуктивностей, соединенные последовательно и встречно, совместно с конденсаторами 9 (С) образуют резонансные контуры, активные потери в которых учитываются резисторами 8 -(R) и 11, имеют проводимость G. Считаем W. W, W.
Среднюю собственную частоту uj резонансных контуров можно изменять путем выбора соответствующей частоты накачки и (или) интенсивности тока накачки. При выполнении условий квантового пазонного резонанса средние собственные колебания (88л.К) резонансного контура будут усилены и через обмотки 4 и 5 и резистор 8 переданы в соседний резонансньм контур и т.д.
Устройство предназначено для моделирования дифференциальных преобразог ваний колебательных и яолновых функций существенно нелин йных систем. Для многих задач нелинейную зависимость отклика системы В (магнитная индукция в сердечнике) на внешнее воздействие после накачки i можно аппроксимировать гиперболическим
синусом i -- ShpB (фиг.2а), где
0 и ft коэффициенты аппроксимации; 1 - средняя длина магнитной линии в сердечнике.
Тогда (фиг.1) может решать FZ-уравнение относительно тока i,(x,t) (аналох ичное PZ - уравнение получается и относительно U(x, t) вида:
I
(t)
9i 3t
(t)i; (1)
(2)
sw
--p
L (t),Lq(t) - первая и вторая произ- водные Ъл,;
S - сечение магнитного сердечника.
Моделируют движение в устройстве следующим образом.
.В зависимости от поставленной задачи, с учетом таблицы аналогий, по параметрам оригинала определяют параметры PZf,S и предельные величины пе-
Таблица аналогий
араметр
Емкость С
2 1 LC
кость А Теплоемкость
С Плотность
а-1.1
Cf
Оригинал исследуют на модели, изменяя параметры L, С, R, G, интенсивность и частоту внешнего воздействия, начальные и граничные условия При этом значение величин L С, R, G, i, in, U) , СО определяют качественные и количественные параметры коэффициентов (2) уравнения (1), т.е определяют класс вырожденных уравнений Анализ PZ-уравнения показывает возможность получения из него большо класса математических моделей, в том числе:
1) О - гиперболическое уравнение (уравнение колебания струнь);
2)Т--5 О - параболическое уравСг U
нение (уравнение теплопроводности или диффузии с внутренними источниками) ;
3)---я -г- О - элептическое
о L О t
уравнение Пуассона; ( (t) уравнение Лапласа);
О 4) -- О - уравнение элемента
азоннои системы; di
зЧ
ел -
ах
6) f i
Зк
3t
О - уравнение Хилла; 55
т уравнение с постоянными коэффициентами
ременных (функций состояний) ориги- . нала и модели. Устанавливают на модели соответствующие оригиналу начальные и граничные условия.
Плотность f
D га
dp/dU
5
0
0
0
5
Полученные результаты означают, что PZ-уравнение (1) представляет собой множество (линейных,нелинейных, нелинейно-параметрических) уравнений как в частных, так и в обычных производных. Исходными условиями, опреде ляющими его класс, являются параметры модели, интенсивности и частоты взаи- модействуюпщх колебаний накачки и со бс ТВ енных о
Рассмотрим пазон ный принцип эволюции движения на основе обменных импульсов при увеличении интенсивности поля накачки (фиг.З). Пусть магнитные индукции в сердечнике изменяются по синусоидальному закону « В,, sin о) t. Индукции В ,д (t) (кривые 1 и 2, фиг.Зд) соответствуют двум режимам токов накачки i -- Sh(/3B sin u)t) (фиг.Зг, кривые
1 и 2, i 7i). По характеристике B(i) (аналитически или экспериментально) определяются графики кривых
L и jV- (фиг.36) и La (фиг.Зв) «iim Qi-m
Анализ кривых показывает, что за
период изменения тока i, скорость изменения динамической индуктивности имеет два экстремума (точки а и а ).
Для кривой LQ эти ТОЧКИ ЯВЛЯЮТСЯ
точками перегиба, а физический смысл для этих точек означает переход фер:ромагнитных сердечников из одного сос стояния в,другое. Это связано с энерг 1гетическим состоянием сердечников, следовательно, эти точки являются точками равновесия (устойчивыми или - неустойчивыми), Величину тока накачки i, при которой система переходит из одного состояния в другое, а кривизна характеристики имеет экстремальное значение d B/di max, назовем критической величиной тока перехода, (точка устойчивого или неустойчивого равновесия) и обозначим
J, а фазовьй угол в тока найдем из выражения
0 arcsin 1д/1,
1 а накачки
(7
где амплитуда тока накачки.
По аналогии величины индуктивности магнитной индукции и напряженности в критической точке назовем соответственно критическими индуктивность
g, магнитную индукцию Вд и напряженность Нд,
На фиг.Зе приведен закон изменения функции динамической индуктивности во времени Lq(t) L,(i, t) для
двух режимов i
п
/,
и 1
(кривые 1 и 2 интегральная модуляция La(i, t) ia фиг.Зж показаны скорости изменения динамической индуктивности LQ(t) Lq(i, t). Как видно из этих кривых L Q принимает значение Lg в точках , в и с, с , когда L (L, t) достигает отрицательного или положительного экстремальных значений с координа- ами соответственно Gi и Q f :
К 1 « X
) KI
+ в (TL -еЖг; JK О, 1,-2, 3...; K,j I, 2, 3,...
где Т ц - период изменения динамичес- кой индуктивности, ; На фиГоЗз и it приведены соответственно кривые пазонных колебаний :() - токов в четвертой ) ;и одиннадцатой i,(t) зонах неустойчи- |вости. Б- критических точках вис происходит вложение энергии в систему l(L (i, t) 0), а в точках в ртоор энергии (L(i, t) ,- О). точках вис происходит усиление , а в точках Ь и с - гашение . В промежутке времени б;ч между вложением энергии и отбором происхо- цят свободные колебания, которые зату Ьсают по экспоненте, так как в контуре обмотки, резисторы и конденсатор имею Активные потери R и G.
и с
Интервал времени свободных колебаний в элементе системы можно определить из выражения
- 0
)f
iCD о
- Т - 2S.
Было установлено, что при интенсивных внешних воздействиях (полях накачки) в распределенной пазонной системе наблюдается ряд новых нелиней-- ных эффектов, в том числе исследованных в известных работах, но не нашедших объяснения. Рассмотрим некоторые из них.
: На фиг,2а приведены кривые - частные характеристики пазонных колебаний Ui дня случая, когда средняя собственная частота колебаний поддерживалась постоянной (А) 60 кГц изменени- ем i,. Переход из одной зоны неустойчивости в другую осуществлялся изменением частоты накачки со . При этом наблюдалось кратное рациональное отношение частот и накачки, т.е. выполнялось классическое условие
Q
5
0
5
0
- г, где п 1, 2, 3,
- номер
W 2 зоны неустойчивости..
Частотная характеристика, приведенная на фиг.26 (в соответствующих зонах неустойчивости указа.ны средние собственные частоты 60, 52, 45, 34 и 20 кГц), получена при постоянной интенсивности Накачки, т.е. iff, const. Однако изменение частоты напряжения накачки о) вызвало изменение параметров магнитных сердечников и интегральной индуктивности L, а следовательно, и частоты w.f,. При этом в самих зонах неустойчивости четко выполняется классическое условие ()(, п/2 ш , а при переходе из одной зоны неустойчивости в другую это условие не вьшолняется для фиксированной частоты накачки. Наблюдается смещение критических частот.зон неустойчивости в сторону низких частот to . При этом рабочий диапазон частот накачки сокращается, по сравнению с предыдущим результатом, в 2-4 раза в зависимости от параметров магнитных сердечников 2 и 3 и резонансного контура (фиг,1). Так, согласно фиг.26, при изменении о) от низких частот накачки (в резонансном контуре возбуждаются эысщие ) к высо.ким наблюдается следующее. При со 2 кГц в PZ,S возбуждаются , т.е. частота ujp, 60, кГц, а уже при и)
20 кГц возбуждаются PZjK с частотой Wn 20 кГц, в то время как по классической теории (см, фиг.2а при w 60 кГц - tDn 6.0.кГц) в первой зоне неустойчивости должны возбуждаться колебания, равные 60 кГц. Таким образом, в приведенном случ.ае нарушается известное условие в силу того, что нарушается рациональное отношение частот при переходе из одной зоны неустойчивости в другую. Подобный результат можно получить изменением интенсивности накачки, учитьшая, что частота имеет нелинейную зависимость от тока накачки.
На фиг.2 приведено еще одно свойство нелинейных для частоты накачки, равной 16 кГц, и линейной емкости в контуре 0,11 мкФ (исходное состояние). Если во второй зоне неус- Ьйчивости (п 2) создать условие для двухстороннего жесткого режима (выбором равенства реактивных сопротивлений резонансного контура), то при переходе в первую зону со стороны второй наблюдается мягкий режим возбуждения . В данном случае в первой зоне наблюдается индуктивный характер реактивности.
При переходе в третью зону со стороны второй также наблюдается мягкий режим. Но со стороны четвертой зоны неустойчивости наблюдается жесткий режим, что говорит о емкостном режиме в третьей зоне неустойчивости. Физика процессов связана с изменением средней интегральной индуктивности системы. Как показывает количественный анализ полученньк результатов, и в том случае наблюдается нарушение классического условия соотношения частот to и Ы.
Как 6bufo сказано выше, точки с координатами б и 8 являются критическими (переходными) точками, в которых происходит обмен энергией между системой и внешним воздействием. Рассмотрим эти явления. На фиг.4 и 5 показан механизм возбуждения и обмена энергией соответственно в пятой (п 5) и девятой (п 9) зонах неустойчивости Приняты следующие обозначения: La.- динамическая индуктивность, i и и J, - мгновенные значения тока и напряжения и Р j - мгновенные значения мощности накачки и резонансного контуров.
Как видно из этих кривых, происходит интегральная модуляция Lq и нестационарное возбуждение , причем уменьшение L приводит к увеличению амлл итуды , а увеличение - к их гашению и смещению их фазы на 180° по отношению к фазе ,
В результате взаимодействия контуров накачки и резонансного происходи взаимная модуляция токов накачки и резонансного, что заметно по кривы мощностей Р и Р. При этом наблюдается возбуждение широкого спектра частот на понижение и повьш1ение, регулярный обмен энергий между контурами. Происходит преобразование одно вида энергии в другой (электрической в магнитную, механическую и обратно) преобразование энергии по частоте, формирование радио- и видеоимпульсов благодаря интегральной модуляции энергоемкого параметра. Наблюдается аналогия явлений в микро- и- макросистемах. На фиг,6 приведена волновая функция состояния if (t) (г, д, е), микрочастицы в силовом потенциальном поле и(х) (а, в), с учетом внешних сил F(x) (б) для прямоугольной ямы Е И, где Е - свободная энергия; и,р - постоянньй потенциал. Области I, II и III соответствуют трем квантовым числам п 1, 2 и 3. При переходе из области I в область II, из последней в область III вблизи точек X -Лд и X Лд силы F(x) стремятся удержать частицу в ограниченной области пространства При этом будет наблюдаться финитное (связанное) движение микрочастицы.
Аналогичные процессы (финитное движение) можно наблюдать и в элементе электрической пазонной системы (фиг.7) при интегральной модуляции L(t) (а), с учетом L (t) (б), прямоугольной аппроксимации L(t) (в) (области I, II, III) для средних собственных колебаний U(t) (г, д, е в первых трех зонах неустойчивости (п 1, 2, 3). Следует сказать, что процессы в квантовой системе можно описать PZ-уравнениями, если в качестве независимой переменной взять пространственную координату.
Таким образом, устройство представляет единую структурно-функцио-. нальную модель, воспроизводящую структуру, состояние и поведение моделирующих систем различной природы.
Связи и взаимосвязи системы и ее свои сггва обеспечивают выполнение определен- Hfiix функций о В качестве функций могут выступать изменяющиеся в пространстве - времени, пространстве или во времени материальные (структурные) и (илн. энергетические параметры системы. Таким образом, функция связана с процессами, проходящими согласно программе, задоженной в самой структуре системы и реализуемой при соответствующем внешнем воздействии. Это характерно для систем различной при- рэды (социальной, экономической, химической, электромагнитной, механической и др.).
Рассмотрим закономерности физических процессов в нелинейной пазонной системе. Внешнее воздействие осуществляете генератором накачки. Зависимость B(i) (фиг. За) является основной характеристикой одного из нелинейных эпементов системы. Крутизна этой характеристики (параметр) Ln dB/dl (|)иг„3б) описывает скорость изменения индукции магнитного поля и определяет процессы в системе, в том числе энергетический обмен. Кривизна крутизны L (i) max (фиг.Зв) указывает на осуществление особых точек, точек перехода из одного энергетического состояния в другое.
Особыми критическими точками могут
бь1ть переход системы из одного упорядо, ют обменное взаимодействие во всех
ченного состояния в другое, взрыв при химической реакции, превышение физиологических нагрузок живого организма критическое значение концентрации и др. Критические точки соответствуют процессам, когда какие-либо величины (параметры) обращаются в бесконечност Е| некоторый конечньй момент времени, гЬичем эти процессы нестационарные, еЫстро растущие во времени явления - Катастрофа. Критические точки с коор- инaтaми 9 j будут соответствовать . Странным аттракторам (отталкивания), 4 с координатами б - аттракторам гфитяжения.
В реальных процессах не всегда гфоисходят катастрофы, так как суще- 4твуют причины, ограничивающие эти $1вления.
Следует отметить еще одно интерес- ijoe явление - самоорганизацию системы 1ак, при увеличении i (поля накачки) j oмeны объединяются, превращаясь В; фдин объемный домен, а при уменьшении
снова восстанавливаются доменные области и т.д. В этом случае домены служат элементом обратной связи самоорганизующейся системы. Информация о характеристиках и состоянии процессов выражается посредством информативных параметров. Lg, Ln(t), L (i ), L (t), i.. Ч. ,в ,.
Сводка основных положений единого закона развития систем с различной формой движения материи (диалектика развития систем).
интегральная модуляция параметра системы, происходит импульсная модуляция параметра по длительности и переход системы из одного состояния в другое в критических точках, увеличивается интервал времени между критическими точками за период изменения параметра.
на 180 по отношению фазы , наблюдается преобразование непрерьшной энергии в ударные импульсы. Отсутствуют мгновенные переходы в системе- Разнополярные импульсы обсулавлива
5
0
0
пазонных системах
в зонах не нарушается рационально 5 отношение частоты средних собственных колебаний и частоты накачки.
е интегро-дифференциальных PZ-уравне- ний.
13
с различной формой движения материи благодаря изоморфизму PZ-уравнений.
Ф,ормула изобретения
Устройство для моделирования динамических объектов, содержащее Ы параметрических зонных систем, каждая из которых снабжена двумя магнитными сердечниками с резонансными обмотками и обмотками накачки и RC-фильтром, который подключен к последовательно и встречно включенным резонансным обмоткам магнитных сердечников, обмотки накачки магнитных сердечников соединены последовательно и согласно и подключены одним из свободных выводов к входу задания напряжения накачки системы, отличающееся тем, что, с целью расширения области
и
п
и.
1115(n -ffO51
Чп
11
/5
16 Ш
Ю 15.в
16
1529254
14
применения, в него введены блок модет лирования активных потерь, выиоппен- ный в виде токозадающего резистора и резистора задания тока накачки, кото рый включен между другим свободным выводом обмоток накачки и шиной нулевого потенциала, общий вывод RC- фильтра токозадающего резистора и блока моделирования активных потерь . i-й (i . 1... (п-1) ) параметрической зонной системы подключен к свобод ному выводу резонансных обмоток (1+)-й параметрической зонной системы, свободный вывод резонансных обмоток первой параметрической зонной системы является информационным входом, а общий вывод RC-фильтра N-й параметрической зонной системы - выходом устройства.
1
(М:кгц
W
50
3V
60 W/cfif
(,кГц
15
17
W
Zf /12
чг 48
В1. ,г
76 (Jtfn
Фиг.г
I }
,/
.З
%V vV
Uft
1 I I л XT I г I I V/
2
а Li
ЛЛУ. iAAJ
д РП,
s.
-Xg,
M Хо X g
I /:
А
fW I
UM
Л
V
ш
т Л|
-.
/i-2
фие.б
oJi
Фи.5
ш
/i-2 и
e
Фиг.
| Мандельштам Л.И., Папалекси Н.А | |||
| Полное собрание трудов, М,: АН СССР, 1947, т.2, с.66, рис.1 | |||
| Авторское свидетельство СССР № 1216811, кл | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1989-12-15—Публикация
1987-06-10—Подача