Изобретение относится к горному . делу, преимущественно к бурению взрывных скважин на открытых горных разработках, а также к геологоразведочному и глубокому бурению, и может быть использовано для оптимизации режимов бурения станками типа СБШ, СВР в угольной, рудной, строительной и др. отраслях промышленности.
Целью изобретения является повышение эффективности управления процессом бурения в условиях разбуривания перемежающихся по свойствам горных пород.
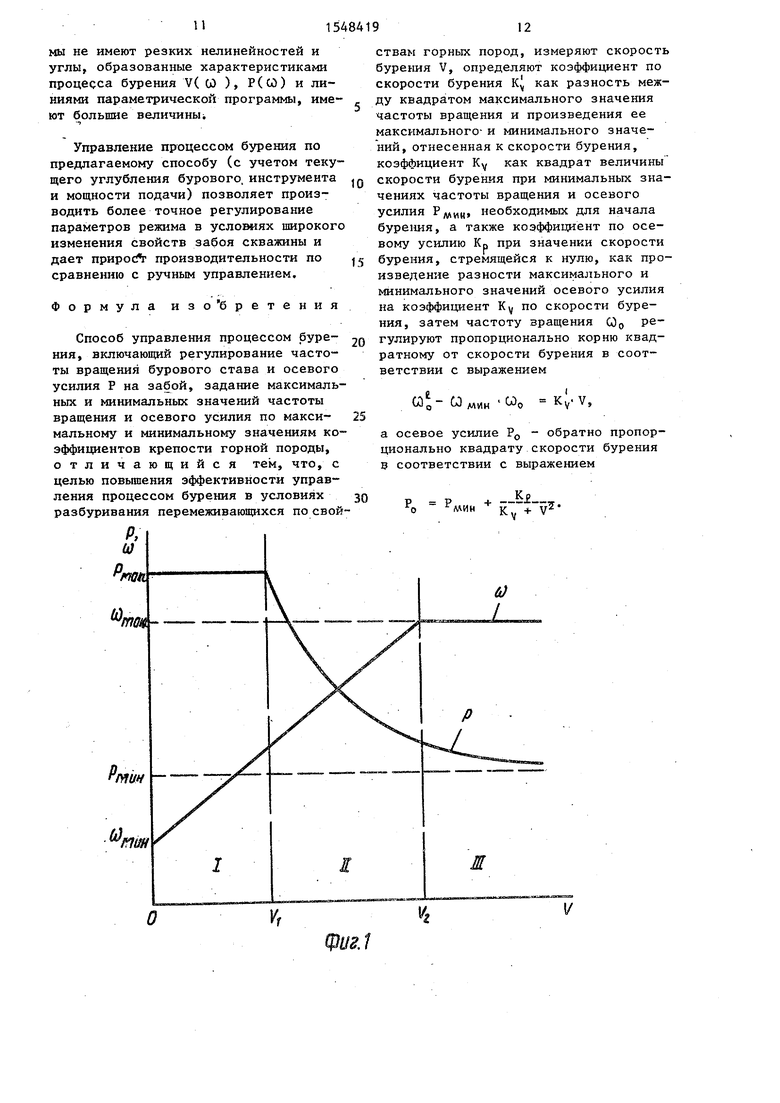
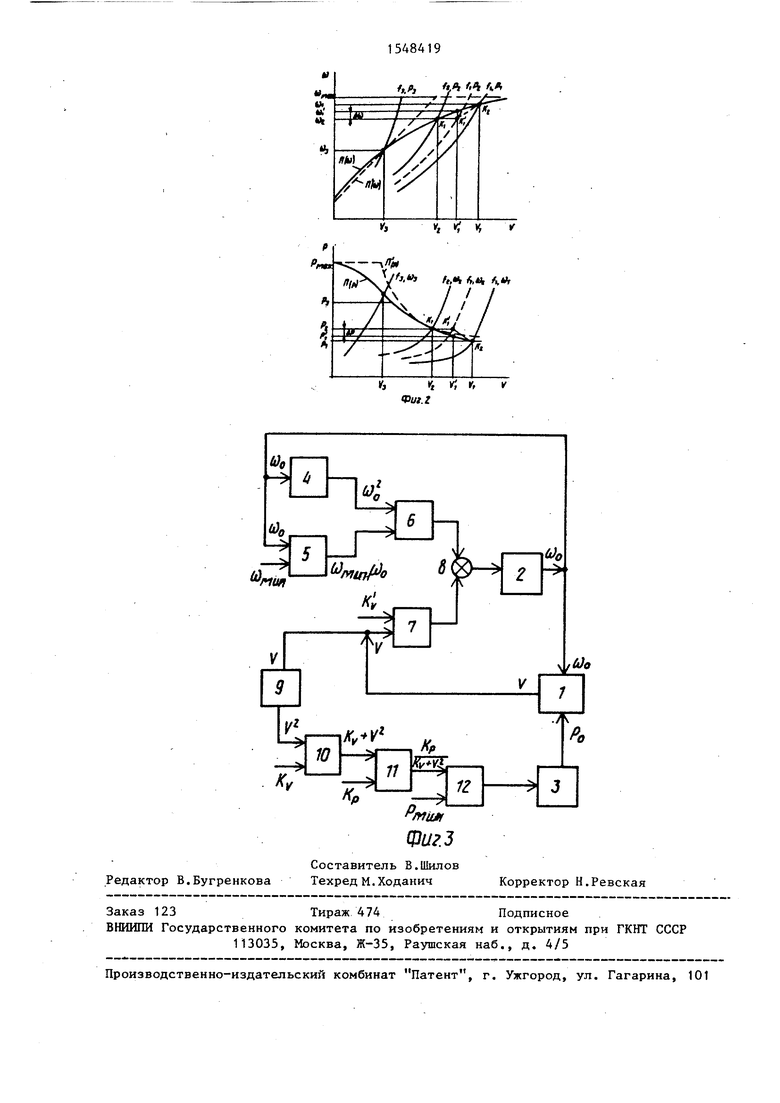
На фиг.1 изображены стандартные iпараметрические программы регулирования СО (V), P(V)i на фиг.2 - параметрические программы регулирования П((0), П(Р) по предлагаемому способу; на фиг.З - вариант блок-схемы устройства для оптимального управления процессом бурения, реализующего способ.
Для повышения эффективности управления и регулирования параметров реО
жима бурения при бурении перемежающихся по свойствам горных пород необходимо учитывать углубление бурового инструмента V/CO за один оборот ,. его вращения и мощность подачи Р0 V, реализуемую на этом инструмента, так как при неучете этих величин происходит потери производительности, особенно большие при изменении крепости f JQ горных пород в широких пределах (практически при бурении взрывных скважин величина f меняется от 2 до 12-15 - для угольных разрезов, от 6 до 20 - для рудных карьеров).15
Таким образом, должно быть
Ц СО„ИН + POV . (1)
Известны параметрические программы регулирования в виде следующих уравнений
K«-V; РП
к 1
PV
(2)
где Кр, KV - постоянные коэффициенты. С учетом ограничений по ряду параметров (Р, СО ,V и т.д.) программы принимают вид, показанный на фиг.1. Для них характерно наличие начальных (при ) значений частоты вращения СОМИН и осевого усилия Рмакс. С учетом этих условий
n -n +K V- Р - к - - -й2ЬЈ. vv о fv V
(3)
Физический смысл введения 03
мин
Рмакс заключается в том, что в первый момент бурения необходимо придать буровому инструменту начальную частоту вращения и осевое усилие, без которых бурение невозможно
Физический смысл коэффициента К„, как видно из уравнений (1), заключается в том, что он определяет мощность подачи, удельную по скорости бурения V. В теоретическом смысле этот коэффициент является характеристикой гиперболы Кр, определяющей забойный процесс при бурении. Коэффициент Ку определяет величину, обратную приросту углубления долота при изменении частоты вращения„ Оба коэффициента (Кр, Ку) определяют пара- ,метры программы регулирования (пара.
0
5
Q
5
0
5
0 5
метрическую программу), которая в данном случае является нелинейной, гиперболической, что обуславливается нелинейностью (гиперболическая зависимость) самого забойного процесса.
Рассмотрим теперь параметрические программы на фиг.1 более подробно. Видно, что уравнение СО(V) имеет вид линейной функции, а уравнение P(V) выражается обратно пропорциональной (гиперболической) зависимостью только в области до РМ01КС и , в то время как величина V может принимать значение, меньшее V4 и большее V2 (величина VMo,KC зависит от конструкции системы подачи бурового станка и типа долота). Конструктивные ограничения станка на и со макс создают зоны регулирования по Р и СО , где имеются изломы параметрических кривых регулирования (зоны I и III). Любые нелинейности статических характеристик вызывают ухудшение динамики процесса. Имеются также технологические соображения в пользу сглаживания параметрических программ. Это, прежде всего, учет углубления долота V/Q и мощности подачи долота на забой PV. Для фиг.1 углубление долота V/СС сохранить постоянным можно лишь в зонах I и II, а в зоне III величина его резко меняется. Для мощности подачи PV установленную мощность можно поддерживать лишь в зонах II, III, а в зоне I эта мощность уменьшается. В любом случае требуются корректировки параметрической программы, чтобы не допускать потери мощности на подачу и превышение углубления долота, что может вызвать бурение корпусом, влекущее к большим непроизводительным расходам мощности и износу долота. Таким образом, параметрические программы регулирования, применяемые в настоящее время, имеют существенные недостатки. Поэтому предлагается способ управления процессом бурения, в котором применяются параметрические программы регулирования с учетом углубления --и мощности P-V подачи. со
Вводя вместо V и Р в уравнение (3) веVличины -jTT- и P-V, получим
Ц «миЛ™-; P0V
КР V
(4)
ь15484
От полученных уравнений (4) м$кно легко перейти к уравнениям регулирования. Для (4а) имеем
(5)
0 W мин 14V (Л
Для оптимального процесса бурения характерно оптимальное значение уг- ю
лубления Обозначим его , после
СОП
чего предьщущее уравнение принимает вид
о С00 KJ,.V.
(6)
Далее, для (4б) можно написать
р - КЈ о уг
(7)
Практическое использование уравнения связано с необходимостью введения первоначального значения осевого усилия Рмин, без которого бурение не может начаться
5
0
5
196
чения осевого усилия и скорости бурения; коэффициент Kv определяет квадрат величины скорости бурения при минимальных установочных значениях параметров режима СОМИН , РМИН необходимых для начала бурения.
Физический смысл полученных выражений (6) и (10) состоит в том что и уравнений (2). Они определяют траектории перемещения координат объекта при оптимальном ведении бурового процесса. Однако предлагаемые траектории имеют существенные отличия от известных. На фиг.2 изображены две пары известных П ( СО ), П (Р) и предлагаемых П((0), П(Р) траекторий, из которых видно преимущества предлагаемых.
Уравнения регулирования (парэмет™ ,рические программы) могут быть выражены как в явном, так и неявном виде. Это зависит от удобства их использования в технических средствах. Суть уравнений от вида их выражения не меняется. Так, для 6Э0 имеем две формы уравнений (в неявном и явном виде):




| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения прочности горных пород в процессе проводки скважины | 1989 |
|
SU1675551A1 |
| СПОСОБ ВРАЩАТЕЛЬНОГО БУРЕНИЯ СКВАЖИН | 2001 |
|
RU2215109C2 |
| Способ управления процессом двухстадийного бурения | 1986 |
|
SU1479630A1 |
| СПОСОБ АДАПТИВНОГО РЕГУЛИРОВАНИЯ УСЛОВИЙ БУРЕНИЯ СКВАЖИН И ДОЛОТО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2499887C1 |
| Способ регулирования условий процесса бурения скважин и устройство для его реализации | 2016 |
|
RU2648731C1 |
| Способ определения энергоемкости процесса разрушения горных пород при бурении скважины | 1990 |
|
SU1742477A1 |
| Устройство для контроля забойных параметров по гидравлическому каналу связи | 1989 |
|
SU1716122A1 |
| СПОСОБ РЕГУЛИРОВАНИЯ УСЛОВИЙ ПРОЦЕССА БУРЕНИЯ СКВАЖИН | 2017 |
|
RU2642699C1 |
| Способ определения прочности горных пород и устройство для его реализации | 2019 |
|
RU2716631C1 |
| Устройство для автоматическойОпТиМизАции пРОцЕССА буРЕНия | 1977 |
|
SU798277A1 |

Изобретение относится к бурению скважин и позволяет повысить эффективность управления процессом бурения в условиях разбуривания перемежающихся по свойствам горных пород. Новые параметрические программы регулирования позволяет учитывать углубление бурового инструмента за один оборот и мощность подачи. Для определения нелинейных параметрических программ, соответствующих нелинейным характеристикам процесса бурения, рассчитываются три коэффициента. Первый коэффициент по скорости бурения (СБ) устанавливают равным отношению разности квадрата минимального значения частоты вращения (ЧВ) и произведения ее максимального и минимального значений к С6. Второй коэффициент по СБ устанавливают равным квадрату величины СБ при минимальных значениях ЧВ и осевого усиления (ОУ). ТРЕТИЙ КОЭФФИЦИЕНТ ПО ОУ УСТАНАВЛИВАЮТ ПРИ ЗНАЧЕНИИ СБ, СТРЕМЯЩЕМСЯ К НУЛЮ, РАВНОМ ПРОИЗВЕДЕНИЮ РАЗНОСТИ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЗНАЧЕНИЙ ОУ НА ПЕРВЫЙ КОЭФФИЦИЕНТ ПО СБ. Затем ЧВ регулируют пропорционально корню квадратному от СБ. Одновременно ОУ регулируют пропорционнально квадрату СБ. 3 ил.
Р + & гмин уа.
(8)
Величина Рмии определяется обычно свободным весом бурового снаряда, без принудительной подачи. В начальный момент бурения при приложении к буро- вому снаряду значений параметров режима, равных Q МИн и Рмин , наблюдается начальное значение скорости бурения VMHH. Выделим эту величину из полного значения скорости бурения V
+VW ve(V2 +2V .V(0+V(°Z) v VMMH v v v
KV+V
oz
(9)
Подставляя полученное выражение (9) в предьщущее уравнение (8) и опуская для удобства индекс (1-штрих), получим
мин
+ -Kj
(10)
В уравнениях (6 и 10) обозначены о W MVIH - оптимальное и минимальное значения частоты вращения бурового снаряда V - скорость бурения; Р0,
мин
- оптимальное и минимальное зна30
Юо- 00МИН W0 VV; (11)
СО мин
К мин
- KV-V. (12)
Если использовать в устройстве управления уравнение формы (12), то надо применить два делителя, квадратор, умножитель, два сумматора, вычислитель копня. Итого надо иметь семь ячеек, три из которых (делитель, вычислитель корня) имеют малую аппаратурную точность. Использование в устройстве управления уравнения формы (11) позволяет обойтись четырьмя ячейками (один квадратор, один сумматор, два умножителя), причем аппара- турно мало точные элементы в этом случае отсутствуют. Неявная форма (11) уравнения (6) более выгодна технически.
Уравнения размерностей имеют следующий вид
и-ый«.йч§даМ
кс
к,
4н|
I -Ш
Таким образом, коэффициенты KV,
K V в уравнении (6) и Kv - в ур нии (10) желательно получить р (например, когда в устройстве ления предполагается использов один задатчик величин Ку и Ку, удобно для практики), то требу решение системы уравнений или ческий подбор коэффициента уси (выбор масштаба) блока 7 или 1 (фиг.З). В любом случае оба ко ента задаются в виде электриче величин (например, в вольтах н жения) .
В соответствии с приведенны уравнениями регулирования (6) необходимо первоначально устан минимальные значения СО
Кр Kv - размерные. Их размерности разные. С технической точки зрения все величины уравнений могут зада- 10 ваться электрическим путем (что и осуществляется во всех устройствах электрического типа). При этом преобразователями величин и размерностей, а также средствами нормировки в совре- 15 меиных технических устройствах служат электрические аппараты (блоки, ячейки) и трудностей это не представляет. Недостаток, связанный с невозможностью настройки клапана гидросистемы 20 мальные величины COWO,KC рмакс
мин раметров, затем назначить их м
После установления величин рмин 1 Kv KV Kp Уравнения (6) приобретают следующий вид
25
30
по всему диапазону регулирования, в предлагаемом способе устраняется, пу- тем формирования (вместо использования естественной) искусственной характеристики (параметрической программы) согласно уравнениям (6) и (10) на основе применения стандартных уз- лов (квадраторы, умножители, сумматоры, делитель),
Таким образом, параметрическая программа, в основе которой может лежать как критерий минимума себестоимости, так и другие, в том числе частные, критерии, в предлагаемом способе совпадает с естественной характеристи- 35 кой забойного процесса уже не в одной точке, а во всем диапазоне регулирования, так как подчиняется тем же закономерностям гиперболы, как и в объекте (процессе) бурения.
Блок-схема устройства для оптимального управления процессом бурения содержит объект I (буровой ста- юк) с регуляторами частоты вращения 2 и осевого усилия 3, квадраторы 4 и 9, умножители 5 и 7, сумматоры 6, 10 и 12, делитель 11 и элемент 8 сравнения.
40
45
В общем случае для вычисления коэффициентов Kv, Ку и Кр нужно решить систему уравнений (6) и (10). Однако это неудобно для практики. В частных случаях, когда параметрические программы заданы первоначально в виде графиков, достаточно каждый из этих графиков описать метаматическими выражениями независимо друг от друга. Если численные значения коэффициентов
419 8
K V в уравнении (6) и Kv - в уравнении (10) желательно получить равными (например, когда в устройстве управления предполагается использовать один задатчик величин Ку и Ку, что удобно для практики), то требуется решение системы уравнений или ческий подбор коэффициента усиления (выбор масштаба) блока 7 или 10 (фиг.З). В любом случае оба коэффициента задаются в виде электрических величин (например, в вольтах напряжения) .
В соответствии с приведенными уравнениями регулирования (6) и (10) необходимо первоначально установить минимальные значения СО
10 1520 мальные величины COWO,KC рмакс
мин мин па раметров, затем назначить их максимальные величины COWO,KC рмакс
После установления величин СО МИц , рмин 1 Kv KV Kp Уравнения (6) и (10) приобретают следующий вид
25
а)
«о В
U0 CV,
б)
(13)
+ F;V
где B,C,D,E,F - постоянные величины.
Первое уравнение (13а) можно выразить в явной форме
В
К
+ CV.
(14)
Частота вращения С00 в этом уравнении пропорциональна корню квадратному от единственной переменной величины - скорости бурения V. В то же время, как видно из (136), осевое усилие Р0 обратно пропорционально квадрату единственной переменной величины - скорости бурения V. Минимальные и максимальные значения частоты вращения со мин , W Mokc и осевого усилия Рмин, PwaKC устанавливаются в соответствии с диапазоном горных пород, залегаемых на обуриваемом блоке. При этом для породы наиболее крепкой (коэффициент крепости Јмакс) должно быть установлено минимальное значение СО /Q мйц (и максимальное - Р/РМ(т); для породы наименее крепкой () - максимальное значение для 03 /со макс(и минимальное для Р/РАДИМ). Величины Рмин , Рмошс , О) мин , могут быть определены по общеизвестным зависимостям. Кроме того, максимальные значения )с , СО длакс определяются возможными параметрами буровых станков.
Согласно предлагаемому способу диапазон регулирования определяется величиной Р
мим
+ -- при (уравне- Ki/
ние 10). Согласно этому способу первоначально устанавливают коэффициент по скорости бурения Ку равным удельной по скорости бурения разнице между квадратом максимального значения частоты вращения и произведением максимального и минимального значений этих частот
К„
.
СОддакс
:
т.е. при этом полагают С00 СОмакс- Затем устанавливают коэффициент Kv равным квадрату величины скорости бурения при минимальных значениях частоты вращения СОМИН и осевого усилия Рмин, необходимых для начала бурения.
Следующим этапом вводят коэффициент по осевому усилию на забой Кр при значении скорости бурения, стремящимся к нулю
Kp-( Ку-( Рубаке мин
После этого ведут бурение в соответствии с уравнениями (6) и (10), учитывающими как углубление долота V/00, так и мощность подачи PV. Регу- лирование при включении устройства в работу производится автоматически по сигналам, вырабатываемым элементом 8 сравнения и сумматором 12, либо может производиться вручную по этим же сигналам оператором станка таким образом, чтобы разница в показаниях устанавливаемых значений СО и Р и оптимальных С00 , Р0 была равна нулю.
Учет углубления долота V/G3 дает возможность обеспечивать заданную производительность бурения на всех породах и диапазонах залегаемых пород на блоке, причем диапазон этот учитывается устанавливаемым диапазоном регулирования параметров режима бурения
Система управления процессом бурения по предлагаемому способу является устойчивой, что видно из рассмот
,
15
20
25
Q
35
дс
.
50
55
рения фиг.2, на которой изображены характеристики процесса бурения СО(V) и P(V), относящиеся к породам с коэффициентом крепости f4, f 2 , f, а также параметрические программы регулирования П(Р), П (Р), П(Ј0), П (О), соответствующие предлагаемому способу (сплошные линии) и известному способу (пунктирные кривые). Сие- тема управления может работать как при одновременном регулировании обоих параметров режима (Р и СО ), так и при попеременном или раздельном их регулировании (один из параметров может регулироваться, а другой - поддерживаться на постоянном уровне). Во всех случаях система устойчива. Разберем наиболее сложный случай - одновременное регулирование обоих параметров. Допустим, первноначально бурилась порода fЈ, что соответствовало установившимся величинам параметров бурения VЈ,(A)Z .Р. Затем порода скачкообразно изменялась и стала f1. Вследствие этого изменилась величина скорости бурения и стала равной V(. Но в программе регулирования заложено, что при значении скорости бурения V, параметры режима СО и Р должны быть равны
С0| и Р( . По сигналу рассогласования система управления установит эти значения параметров в соответствии с уравнениями СО1, С f (V,1 ) , Р, (V,) J , где в квадратных скобках указан модуль функции f(V). На графиках сигнал рассогласования пропорционален величинам UCO СО ,-Сд) UP Р|-Рй. Система бурения перейдет в промежуточную точку с координатами СО , , Р1, , V, . Этот процесс перехода продолжается до тех пор, пока не установятся новые -значения ( P( , V , соответствующие новому значению характеристики f, породы. Видно, что процесс - сходящийся (величина рассогласования ьсО , &Р, уменьшается до нуля), Траектория системы показана на фиг.2а,б пунктиром от точки Kt через К| к К. Аналогично можно проследить другие случаи перехода системы управления к другим координатам вследствие случайного изменения свойств горной породы в процессе бурения. Как видно из графиков фиг.2, система управления по предлагаемому способу обладает большей устойчивостью по сравнению с известными, поскольку ее параметрические программы не имеют резких нелинейкостей и углы, образованные характеристиками процесса бурения V((0 ), Р(О) и линиями параметрической программы, имеют большие величины.
Управление процессом бурения по предлагаемому способу (с учетом текущего углубления бурового, инструмента и мощности подачи) позволяет производить более точное регулирование параметров режима в условиях широкого изменения свойств забоя скважины и дает приройт производительности по сравнению с ручным управлением.
Формула изо бретения
Способ управления процессом буре- ния, включающий регулирование частоты вращения бурового става и осевого усилия Р на забой, задание максимальных и минимальных значений частоты вращения и осевого усилия по макси- мальному и минимальному значениям коэффициентов крепости горной породы, отличающийся тем, что, с целью повышения эффективности управления процессом бурения в условиях разбуривания перемеживающихся по свойР, Ц
WA
ti,
menPMUH.Ь).
пан
ствам горных пород, измеряют скорость бурения V, определяют коэффициент по скорости бурения К как разность между квадратом максимального значения частоты вращения и произведения ее максимального- и минимального значений, отнесенная к скорости бурения, коэффициент Ку как квадрат величины скорости бурения при минимальных значениях частоты вращения и осевого усилия РМИн необходимых для начала бурения, а также коэффициент по осевому усилию Кр при значении скорости бурения, стремящейся к нулю, как произведение разности максимального и минимального значений осевого усилия на коэффициент Kv по скорости бурения, затем частоту вращения С00 регулируют пропорционально корню квадратному от скорости бурения в соответствии с выражением
са - со
мин
Юй
KyV,
а осевое усилие Р0 - обратно пропорционально квадрату скорости бурения В соответствии с выражением
р р + -ЈЈ, о мин К„ + V
6)
| Способ управления процессом бурения | 1969 |
|
SU479866A1 |
| Выбрасывающий ячеистый аппарат для рядовых сеялок | 1922 |
|
SU21A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ БУРОВЫМИ СТАНКАМИ | 1961 |
|
SU148367A1 |
| Выбрасывающий ячеистый аппарат для рядовых сеялок | 1922 |
|
SU21A1 |
Авторы
Даты
1990-03-07—Публикация
1988-05-18—Подача