Изобретение относится к электродинамике двухсвязных систем передачи электромагнитной э.нерги;и, например к электродинамике однородной двухпроводной или полосковой линии передачи электромагнитной энергии, и может применяться в линиях передачи, антенной технике и технике сверхвысоких частот.
Известны линии передачи электромагнитной энергии с волнами типа ТЕМ, напри- мер полоско вые, коаксиальные и двухпроводные. Из теории длинных линий известно, связь между напряжением и током в произвольном сечении линии и пер- . вичными параметрами длиной линии определяется телеграфными уравнениями. Обычно при этом рассматривают однородную длинную линию, любой бесконечно ма- лый участок которой dx обладает индуктивностью dL, емкостью dC, активным сопротивлением dR и проводимостью изоляции между проводами dG. При этом погонные параметры, характеризующие линию, считались неизменными вдоль всей линии и имели размерность
I гГИт.г г -1-R r l-fi Г Сим 1 Lo м Jl о м Ь °1 м J b°l м J
Телеграфные уравнения в комплексной форме имеют вид
d U I(R0 + J .coLo)
dx d I d x
U(G + j « Co)
(D
где ZG Ro + j ft LO - полное комплексное погонное сопротивление линии;
Yo Go + j - полная комплексная погонная проводимость линии.
Решая систему уравнений (1), получают дифференциальное уравнение для напряжения в линии
СЛ
XI
1
00 hO
о
Ш
d2U dx2
,
(2)
где, . .. .
fe Z0Yo (Ro + j со Lo)(Go + j a) Co) -JLoC0 + RoCo + j r/XLoCo + CoRo) (3)
постоянная распространения, характеризующая основные показатели распространяющейся в линии волны. В общем случае
постоянная распространения является величиной комплексной:
У a f j/5,(4)
действительная часть которой а является коэффициентом затухания, а мнимая /3фазовой постоянной (коэффициентом фазы).
Если рассматривать линию без потерь, в которой RO 0 и Со 0, то постоянная распространения в ней из (3) будет равна
V - IP -(5)
т.е. окажется величиной чисто мнимой.
При этом фазовая скорость Уф распространения волны в линии определяется через фазовую постоянную (3 и частоту 0)v получается равной
(6)
Р VUCo
Из этой формулы видно, что фазовая скорость волны в длинной линии без потерь зависит только от реактивных погонных параметров линии LO и Со и не зависит от частоты, откуда делается вывод о том, что двухпроводная длинная линия, в отличие от волновода, т.е. от односвязной системы, не обладает дисперсионными свойствами.
Известны конструкции полосковой, коаксиальной и двухпроводной линий передачи электромагнитной энергии, содержащие два токонесущих проводника, отстоящих один от другого на расстоянии, значительно меньше длины рабочей волны.
Одним из свойств известных линий является отсутствие положительной диспер- сии в них. Это свойство в некоторых практических случаях оказывается недостатком линий такого типа. Так, например, фазовая длина волны определяется в них только параметрами диэлектрика и не мо- жет быть больше длины волны в свободном пространстве. Это свойство является препятствием для выполнения линий с меньшим набегом фаз, чем позволяет их естественная длина и при изготовлении шм- рокополосных устройств на основе длинных линий, таких как направленные ответвите- ли, мосты, вибраторные антенны и т.п.
Известны радиочастотные линии передачи электромагнитной энергии, содержа- щие два токонесущихпроводника,
расположенных параллельно один другому, по крайней мере в один из которых последовательно включены одинаковые емкости, обладающие свойствами полосно-пропу- екающих фильтров При увеличении количества включенных в линию емкостей обычно усиливают фильтрующие свойства и следовательно увеличивают задержку движения энергии в такой линии Такие линии не обладают положительной дисперсией, а скорость движения фазы волны в них не может быть больше скорости свега.
Цель изобретения - придание двухсвязной радиочастотной линии дисперсионных свойств (положительной дисперсии).
Поставленная цель достигается тем, что хотя бы в один из проводников двухсвязной линии дополнительно введены последова1- тельно включенные, равномерно распределенные по всей длине емкости. При этом емкости могут быть выполнены как сосредоточенные в виде емкостных включений, так и распределенные в один или в оба провода линии.
Для доказательства возможности получения дисперсионных свойств рассмотрим однородную двухпроводную длинную линию с включениями, эквивалентная схема которой имеет вид. показанный на фиг. 1.
Or ранее рассмотренной онэотличается равномерно распределенной по всей длине емкостью Сь, включенной последовательно в каждый элемент dx линии. При эгом погонные параметры такой линии будут иметь размерность
Сим
1 Г Гн 1 Г Г Ф 1 Р Г °М 1 Г
L°t--,,,Go
V Kl|V| -I
м1.
Полное комплексное погонное сопротивление и полная комплексная проводимость такой линии будут равны
Z (Ro + + т);
Y (Go + j (о Со).(7)
Решая аналогично телеграфные уравнения для такой линии, получим следующее выражение, определяющее постоянную распространения волны тока или напряжения1
ZY-Ro + j.;Lo + T)x
х (Go + j a) Co).(8)
Как и прежде, рассмотрим случай, когда активные потери в линии отсутствуют R0 О и Go 0. При этом постоянная распространения будет равна:
OJL.O- L0Co
j о) Сь
р- )j (i) Со
Со
V
(9)
Видно, что в зависимости от частоты (а постоянная распространения может быть величиной действительной, мнимой или равной нулю. По аналогии с волноводами, частоту, при которой постоянная распространения становится равной нулю, назовем критической частотой
X2 - ( UCu + - О откуда
ъ
Ofcp- -гLo Cb
ИЛИ ОДр
Иначе говоря, критическая частота рассматриваемой линии определяется величинами погонной индуктивности и включенной в линию последовательно емкостью Теперь, подставив значение критической частоты в выражение (10), имеем:
у ш
V
$ъ (12)
а
Из полученного выражения видно, что на частотах ниже критической постоянная распространения будет величиной действительной, т.е. волна в двухпроводной линии с включениями распространяться не будет (как в волноводе). На частотах выше критической постоянная распространения будет -величиной мнимой и следовательно будет определяться только изменение фазы распространяющейся волны.
Фазовая скорость в линии с емкостными вставками соответственно определится выражением
рь V i r
|МЭ О .
(13)
X
V
1
О) Lo Cb
Из полученного выражения видно, что 8 двухсвязной линии с последоватепьно включенными емкостАыми вставками, распределенными равномерно по всей длине линии, фазовая скорость зависит от частоты, т.е. в ней проявляется положительная дисперсия.
Не сложно убедиться, что включение в -линию параллельно резктивностей емкостного характера не приведет к появлению дисперсионных свойств рассматриваемой системы.
Заметим также, что формулы 13 и 14 определяют зависимость фазовой постоянной не только от частоты, но и от соотношения погонных параметров L0 и Сь.
Волновое сопротивление линии с включениями определяется вырьжен рм
Z0 /|
(АДср
г
и зависит от отношения рабочей длины водны и критической. Поскольку дл распространяющихся волн это отношение всегда меньше единицы, то можно утверждать, что
волновое сопротивление линии с включени ями всегда меньше волнового сопротивле ния РО такой же линии но без реактивных включений.
5При этом сопротивление линии с включениями, нагруженной на ZH в произвольном сечении х, имеет входное сопротивление, равное
7 ( у 1 - U () - 7 ZH + J Zo tg / X
Ю (TfZo+jZntg/TT (lbj
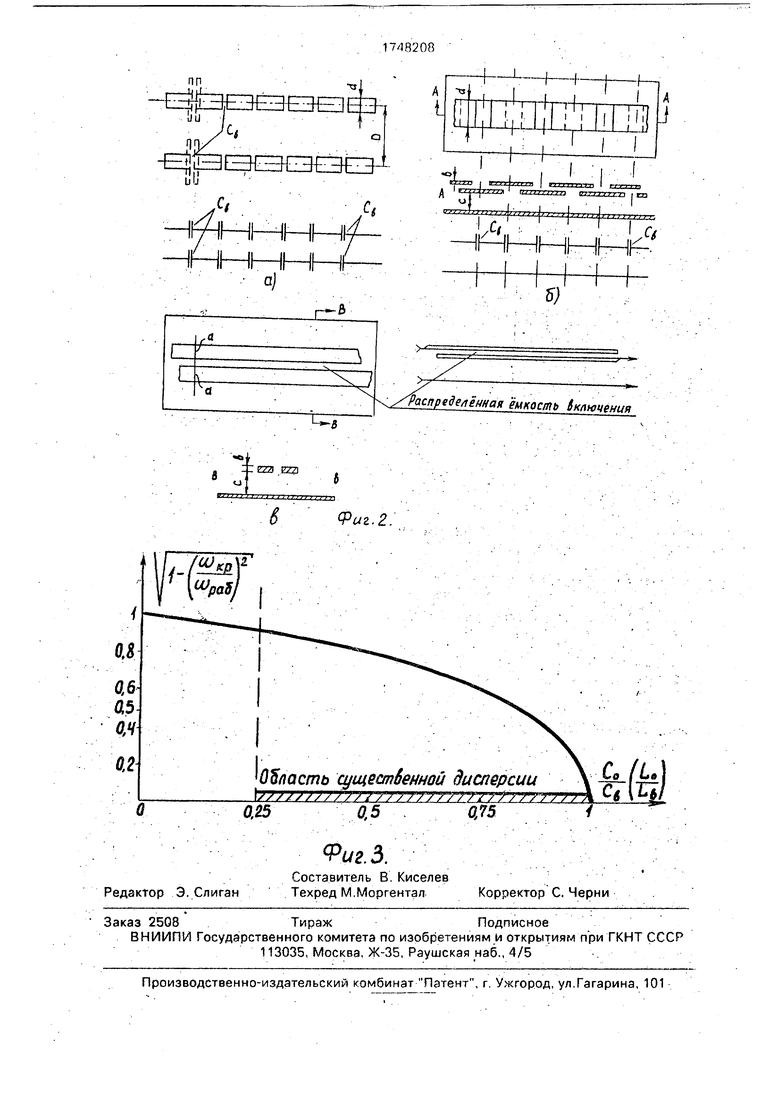
При рассмотрении различных конструкций линий с включениями (фиг. 2) можно увидеть, что реактивные включения могут быть сосредоточенными или распределен15 ными, например, в виде N конструктивных емкостей, распределенных равномерно по всей длине линии (фиг 2.а) или в виде распределенной емкости по всей длине линии (фиг 2, б, в).
20Нетрудно определить соотношение
первичных параметров в линии с включениями, при которых в ней будет наблюдаться явление дисперсии. Нижняя рабочая частота определится выражением
25
Ј 1 ш
(16)
при этом Сь Со,
т е. реактивные включения по величине равны погонным реактивностям отрезков яй30 ним без дисперсии. При выполнении этого условия дисперсионные свойства линии выражены наиболее ярко С другой стороны, есл1 реактивность вставки окажется бол - ше соответствующей погонной реактиьно35 сти, го дисперсионный множитель будет приближаться к един -це и дисперсионные свойства в линии будут проявляться незначительно (фиг. 3).
Изменяя величину дисперсионного
40 множителя, можно изменять электрическую длину линии по сравнению с геометрической дпиной. Это свойство осоебнно важно и может быть использовано при проектировании устройс ва миллиметрового дйапазо45 на радиоволн, существенно увеличивая их размеры
Таким образом, предлагаема радиочастотная линия передачи электромагнитной энергии обладает новым свойством - поло50 жительчой дисперсией волн.
Изобретение иллюстрируется примерами (фиг. 2).
На фиг, 2, а изображена двухп роводнэя линия, в разрывы обоих проводов которой
55 последовательно включены емкости Сь (уст ройстчо и электрическая схема). Изменять величину емкости Сь можно, изменяя конфигурацию разрывов(например, делая их в виде косых щелей), или включая дополнительно в разрывы сосредоточенные емкости При этом необходимо, чтобы емкости были размещены равномерно и на расстоянии, меньше или значительно меньше дли ны волны
На фиг, 2, б изображена несимметрич ная полосковая линия с емкостными включениями (вид сверху, вид сбоку и ее схема) в полосковый проводник, выполненный в виде металлических отрезков полоски, расположенных последовательно, изолированных один от другого и от основания линии Изменяя зазор между отдельными полосками, можно изменять величину емкостей, включенных последовательно в линию передачи
На фиг 2, в изображена несимметричная полосковая линия с последовательно включенной емкостью, распределенной вдоль всей линии (вид сверху, вид сбоку торцовой срез) При этом емкость включения образуется между торцами двух полосок верхнего проводника
Экспериментальные исследования распределения составляющих электромагнитного поля вдоль линии с включениями показали, что фазовая длина волны в такой линии изменяется в зависимости от отноше
ния рабочей и критической частот, т е в линии с реактивными включениями наблюдается явление дисперсии, аналогичное дисперсии волн в волноводе
На основе радиочастотных линий передачи электромагнитной энергии с реактивными включениями можно создавать устройства с уменьшенным набегом фаз, линии задержки с изменяющимся временем задержки для разных частот, фильтры верхних частот, широкополосные антенно-фи- дерные устройства
Формула изобретения Радиочастотная линия передачи, содержащая два проводника расположенных параллельно, по крайней мере в один из которых последовательно включены емкости Сь расположенные на одинаковых рас- стояниях одна от другой, отличающая- с я тем, что, с целью придания дисперсионных свойств и превышения фазовой скорости над -рупповой скоростью, емкости Сь выбраны из соотношения Сь , где С i - емкость между отрезками проводников, расположенных между соседними емкостями Сь



| название | год | авторы | номер документа |
|---|---|---|---|
| Радиочастотная линия передачи | 1990 |
|
SU1748209A1 |
| Вибраторная антенна с емкостными включениями | 1989 |
|
SU1808153A3 |
| КОАКСИАЛЬНАЯ ФИДЕРНАЯ ЛИНИЯ | 2007 |
|
RU2339128C1 |
| ЧУВСТВИТЕЛЬНЫЙ ЭЛЕМЕНТ ДЛЯ ОПРЕДЕЛЕНИЯ ВЛАГОСОДЕРЖАНИЯ ЖИДКОЙ СРЕДЫ | 2006 |
|
RU2330267C1 |
| МИКРОПОЛОСКОВАЯ ФИДЕРНАЯ ЛИНИЯ | 2008 |
|
RU2364995C1 |
| ТРАНСПОНДЕР | 1997 |
|
RU2133482C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЗАМЕДЛЯЮЩИХ СИСТЕМ | 1999 |
|
RU2156473C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЗАМЕДЛЯЮЩИХ СИСТЕМ | 1997 |
|
RU2136008C1 |
| ПЕЧАТНО-ПОЛОСКОВЫЙ ШУНТОВОЙ ВИБРАТОР | 2015 |
|
RU2604348C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЗАМЕДЛЯЮЩИХ СИСТЕМ | 1997 |
|
RU2136010C1 |

Применение: линии передачи, антенная техника и элементы трактов сверхвысокочастотных устройств. Сущность: радиочастотная линия передачи содержит два проводника, расположенных параллельно и по крайней мере в один из которых последовательно включены емкости Сь, расположенные на одинаковых расстояниях одна от другой при выполнении соотношения Сь S Сд I, где Cdi - емкость между отрезкам и проводников, расположенных между соседними емкостями. Обеспечивается наличие дисперсии и превышения фазовой скорости над групповой. 3 ил.
ПП
-Е ЗЕЭЕЭЕЭЭфь
huHi f
uu
II
ЙЗВСЗЕ
У c
тмьчнм )
Фиг. 2.
1 (UpaS/
Отпасть сущестбенной дисперсии
S / / Ј S /
0,25
0,5
Фиг.З.
Определённая ёмкость X,fPmffr
сперсии
0,75
Св (Ц Ci№j7
| Близнюк Н.Р | |||
| Волны вдоль проводов | |||
| КВИРТУ, Киев, 1965 | |||
| Маттей Д.Л., Янг Л., Джонс Е.М.Т | |||
| Фильтры | |||
| СВЧ, согласующие цепи и цепи связи | |||
| Связь, 1971, т | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Термосно-паровая кухня | 1921 |
|
SU72A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1992-07-15—Публикация
1990-10-29—Подача