ел
С



| название | год | авторы | номер документа |
|---|---|---|---|
| Способ получения n- и p-типов протонных полупроводников | 2016 |
|
RU2649649C2 |
| ПРИЕМНИК ИЗЛУЧЕНИЯ | 2008 |
|
RU2391637C2 |
| СПОСОБ ПОЛУЧЕНИЯ ПРОТОННОЙ ПРОВОДИМОСТИ В КРИСТАЛЛАХ И ЭЛЕКТРОИЗОЛЯЦИОННЫХ МАТЕРИАЛАХ | 2007 |
|
RU2360239C1 |
| СПОСОБ КОНТРОЛЯ ПАРАМЕТРОВ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ | 1990 |
|
RU2025827C1 |
| МОДУЛЯТОР ИНТЕНСИВНОСТИ ПОВЕРХНОСТНЫХ АКУСТИЧЕСКИХ ВОЛН НА ОСНОВЕ ПОЛУПРОВОДНИКОВОЙ КВАНТОВОЙ ЯМЫ | 2022 |
|
RU2780001C1 |
| СПОСОБ ПОЛУЧЕНИЯ МАНГАНИТА ЛАНТАНА, ЛЕГИРОВАННОГО КАЛЬЦИЕМ | 2012 |
|
RU2505485C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ГАЗООБРАЗНЫХ ВЕЩЕСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2002 |
|
RU2209425C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ, ЭЛЕКТРОПРОВОДНОСТИ, ЭФФЕКТИВНОЙ МАССЫ, КОЭФФИЦИЕНТОВ РАССЕЯНИЯ НОСИТЕЛЕЙ ЗАРЯДА, КОНЦЕНТРАЦИИ И ЭНЕРГИИ АКТИВАЦИИ ЛЕГИРУЮЩЕЙ ПРИМЕСИ ПОЛУПРОВОДНИКОВОГО СЛОЯ | 2016 |
|
RU2619802C1 |
| СПОСОБ УСТРАНЕНИЯ СТРУКТУРНЫХ ДЕФЕКТОВ В ТВЕРДЫХ ТЕЛАХ | 1997 |
|
RU2124784C1 |
| ПОЛЕВОЙ ТРАНЗИСТОР ШОТТКИ | 1991 |
|
RU2025831C1 |
Изобретение относится к технической физике и может быть использовано для исследования электрических свойств материалов. Сущность изобретения: при различных температурах проводят измерение частотной зависимости малосигнальной проводимости на переменном токе с приложением постоянного смещающего напряжения и без него. Определяют граничную частоту, при которой частотные зависимости совпадают. О прыжковой проводимости судят по направлению сдвига граничной частоты с изменением температуры. 1 ил.
Изобретение относится к технической физике и может быть использовано для исследования электрических свойств материа - лов. -; . ; .:. :.
В настоящее время известен ряд способов определения прыжковой электропроводности в неупорядоченных неметаллических материалах. Одни из них состоит в анализе температурной зависимости проводимости на постоянном токе а (Т)- Теория предсказывает, что при понижении температуры в температурной зависимости прыжковой проводимости наступает Отклонение от активационного закона с постоянной энергией активации - энергия электропроводности начинает уменьшаться с падением Т, и зависимость о (Т) описывается формулой Мотта:
аГТ) аоехр -(| , (1)
где оь постоянная величина; Т0 - параметр Мотта;
i ; .. : .
Отмеченное изменение хода 7(Т) обусловлено переходом от режима R-протеКа- ния, когда прыжки носителей заряда осуществляются на ближайшего соседа и разбросом энергий состояний можно пренебречь, к режиму R-e-протекания, когда прыжки носителей заряда осуществляются вблизи уровня Ферми и разброс электронных состояний по энергиям следует учитывать.
00
Ј о
00
Вывод о наличии в неупорядоченных полупроводниках и диэлектриках прыжковой электропроводности на основании данных по сг (Т) типа (1) был сделан для целого ряда материалов: аморфных элементарных полупроводников, модифицированных халькогенидных стеклообразных полупроводников, аморфных оксидов переходных металлов и др. Однако значения Y часто отличаются от теоретического. Это может быть обусловлено рядом неучтенных в исходной теории причин - корреляцией между энергиями и координатами центров, падением плотности состояний вблизи уровни Ферми из-за электрон-электронного взаимодействия, нестандартным характером температурной зависимости темпов многофононных переходов, наличием температурной зависимости предэкспоменци- ального множителя оь Т . Заметим, что лишь за счет подбора X в интервале от -7,5 до 2,75 можно добиться хорошего согласия экспериментальных данных по гт(Т) аморфных германия и кремния с формулой (1), что выбирая Y в интервале от 0,2 до 0,55. Это говорит о том, что точность определения прыжковой электропроводности по температурной зависимости проводимости на постоянном токе невысока.
И уже во всяком случае анализа а (Т) не позволяет определить тип электронных переходов - а (Т) оказывается одинаковой для туннельных переходов и термоактивиро- оанных прыжков. Более того, формула (1) справедлива при низких температурах и в качественно отличном по самому механизму локализации носителей заряда случае сильной электрон-фононной связи (наличия поляронов) в неупорядоченном материале. При этом моттовской температурной зависимости при понижении температуры предшествуют два участка активационной зависимости с энергиями активаций, отвечающими последовательно энергии меж- узельного поляронного перескока и разбросу электронных состояний по энергиям. Схожесть хода этой зависимости с о (Т) в случае переноса электронов по делокали- зованным состояниям в примесном полупроводнике (см.выше) ставит под вопрос возможность установления по а (Т) в общем случае самого факта прыжковой электропроводности;
Другой способ определения прыжковой электропроводности основан на анализе зависимости проводимости материала на постоянном токе от напряженности электрического поля a(E)(H.Bottger, V.V.Bryksin Hopping Conduction in Solids,
0
5
0
5
0
5
0
5
0
VCB, 1985, pp.241-243). Характеристическим признаком прыжковой электропроводности здесь является наличие в зависимости о (Е) минимума. Начальное падение неомической проводимости с ростом Е может быть связано с двумя обстоятельствами: переходом от изотропного протекания к направленному и захватом носителей заряда на мертвые концы кластера состояний, по которым осуществляется прыжковый перенос, Последующий за участком падения рост а с увеличением Е обусловлен полевой зависимостью вероятности перескока в направлении внешнего поля.
Минимум в зависимости а (Е) наблюдался на эксперименте у целого ряда материалов: легированных полупроводников при низких температурах, аморфных оксидов переходных металлов и др. Вместе с тем эффект сильного поля так же, как и температурная зависимость проводимости, не позволяет определить тип электронных переходов. В то время как с точностью до модели, связывающей падение т(Е) с перестройкой пути протекания тока, наличие ми- нимума о (Е) предполагает термически активированные электронные переходы, захват носителей заряда на мертвые концы кластера состояния безотносителен к типу электронных переходов. Определить, какая. из двух причин падения ас. ростом Е в действительности доминирует, как правило, не представляется возможным.
Описанные аналоги совпадают с предлагаемым решением по целевому назначению, но по совокупности признаков, определяющих достижение положительного эффекта, наиболее близким к предполагаемому решению (прототипом) является способ определения прыжковой электропроводности по частотной зависимости малосигнальной проводимости на переменном токе о ( м ) при различных температурах..
. В неупорядоченном материале с прыжковой проводимостью при наличии широкого разброса темпов перескоков между локализованными состояниями зависимость о (а)) имеет вид
а (({)} А «А
(2)
где А - постоянная величина;
S - показатель, который по величине не превышает единицы и может зависеть от температуры.
Эта зависимость качественно отличается от зависимости f(w) для материалов с
электронной проводимостью по делркали- зованным состояниям, описываемой выражением типа
о (ш )
1
1 +W2T2
где г- время релаксации импульса свободного электрона, составляющее по порядку величины , и предсказывающей постоянство о вплоть до самых высоких частот. Поэтому частотную зависимость проводимости типа (2) можно считать надежным признаком прыжковой электропроводности (правда, только на малом сигнале). На эксперименте степенная о ((а ) наблюдалась у широкого класса неупорядоченных материалов.
Вместе с тем по виду а(а) не удается установить тип электронных переходов, так как формула (2) справедлива для всех указанных типов переходов. Можно пытаться различить бесфононные переходы и термо- активированные прыжки по величине и температурной зависимости показателя степени S, который в двухузельном режиме прыжковой электропроводности на переменном токе должен быть приблизительно равным 0,8 и не зависеть от температуры в случае туннельных переходов и может оказаться близким к единице и уменьшаться с повышением температуры в случае термо- активироёанных прыжков. Однако вывода такого рода являются предположительными, так как величина показателя степени S и его температурная зависимость определяются не только типом переходов, но и режимом прыжковой электропроводности. Так, при переходе от двухузельного режима к режиму многократных перескоков показатель S уменьшается, а его температурная зависимость усиливается. Кроме того, определение показателя S с точностью до сотых долей единицы представляет собой довольно сложную в техническом отношении задачу.
Цель изобретения - повышение точности в части определения типа электронных переходов.
Предлагаемый способ основан на том, что эффект падения проводимости с ростом напряженности электрического поля в области сильных полей проявляется лишь в области относительно низких частот, когда размеры кластера состояний, по которым осуществляется прыжковой перенос L (о), достаточны для того, чтобы на а (а) сказалась перестройка пути протекания тока и/или захват носителей заряда на мертвые
концы кластера состояний, Формально это условие может быть записано следующим образом:
е Е L ((а ) КТ.
(3)
где Е - напряженность электрического поля;
Т - температура;
К - постоянная Больцмана; е - заряд электрона.
Частотная зависимость L ( а)) описывается следующим выражением:
L(ft))N
,-1/3
In
ш
«N
-1/3
1/3
(4)
где Wc - вероятность критического прыжка, определяющая момент возникновения кластера состояний, замыкающего электроды;
- боровский радиус локализованных состояний;
N -. концентрация узлов локализации, по которым происходит прыжковый перенос,
Подставляя выражение (4) в выражение (3), переходим к следующему выражению для граничной частоты а)0 (максимальной частоты, на которой сказывается эффект сильного электрического поля):
а(Г1/3 (
еЕ N
1/3
КТ
(5)
5
0
5
0
5
где с - численный коэффициент порядка единицы.
Из выражения (5) следует, что для электронных переходов различного типа а)0 по- разному зависит от температуры, что обусловлено различным поведением Wc с изменением температуры. В случае.туннельных переходов, когда Wc практически не зависит от температуры, ш0 с ростом температуры падает. При термически активированных перескоках, когда Wc возрастает с увеличением температуры по активацион- ному закону, (t)0 с ростом температуры возрастает.
Таким образом, реализация предлагаемого способа позволяет повысить точность в части определения типа электронных переходов. При этом выбор величины постоянного смещающего напряжения, соответствующей минимуму проводимости (эта величина определяется на основании априорной информации), обеспечивает максимальную точность определения граничной частоты №ъ (хотя принципиально измерения по данному способу можно производить при разных величинах постоянного смещающего напряжения на участке падения проводимости с ростом напряженности электрического поля).
Доказательством существенности отличий предлагаемого решения является то, что в качестве характеристического признака прыжковой электропроводности используют направление сдвига граничной частоты Шо с изменением температуры, а не поведение самой о(ш как это предполагает способ-прототип. При этом удается решить задачу установления типа электронных переходов, недоступную для известных способов-определения прыжковой электропроводности, причем получаемый ответ распространяется на область сильных электрических полей, отвечающую условиям применения многих технических диэлектриков.
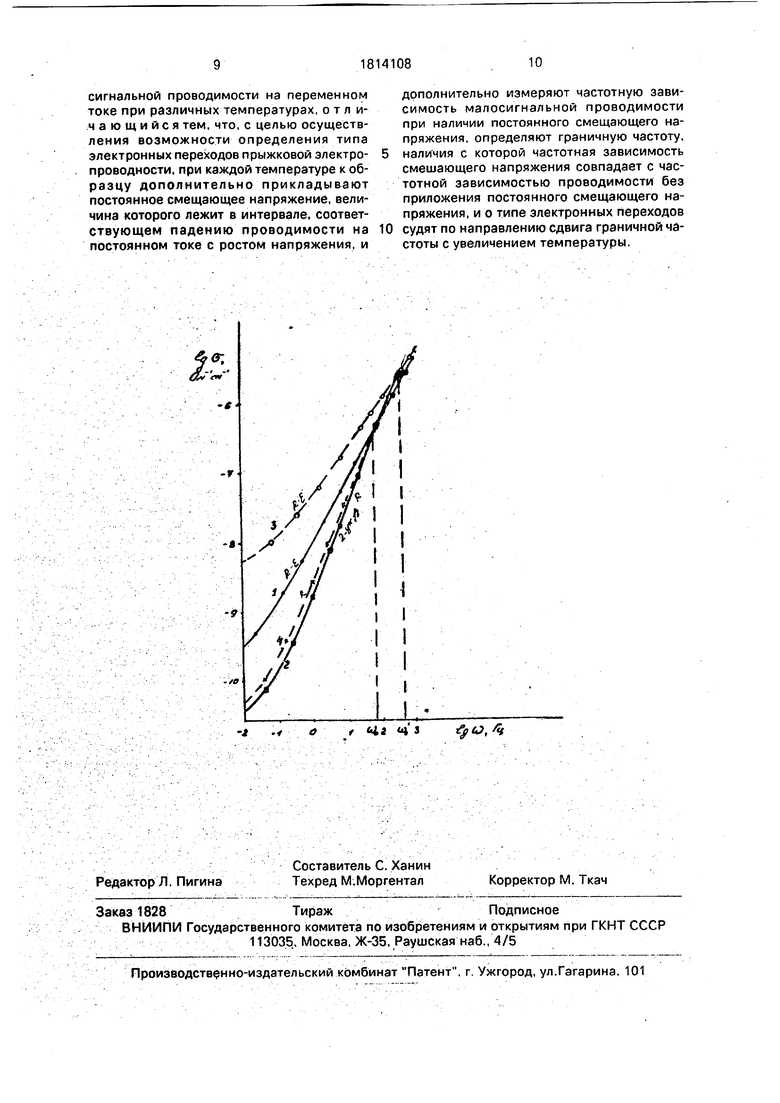
На чертеже представлены графики зависимости проводимости на переменном токе от частоты при температуре 298 (1, 2) и 358 К (3, 4) без приложения постоянного смещающего напряжения (1, 3) и с приложением постоянного смещающего напряжения (2, 4) для анодного оксида тантала.
В качестве примера реализации изобретения приведем данные по определению прыжковой электропроводности в анодных оксидных пленках Та20з. используемых в качестве ра&оты диэлектрика конденсаторов. При двух различных температурах - 298 и 358 К производились измерения о(ш} пленок Ta20s толщиной
о ,.
1700 А в конденсаторной структуре Ta-Ta20s- электролит (38%-ный водный раствор НаЗСм) без приложения постоянного смещающего напряжения и с приложением постоянного смещающего напряжения, соответствующего минимальной проводимости Та20з на постоянном токе и равного 35 В при Т 298К и 38 В при Т 358 К (величины напряжения определялись на основании априорной информации V E0ci, где Ео - напряженность поля, отвечающая минимуму о ; d - толщина пленки. Амплитуда переменного сигнала составляла 100 мВ. Полярность напряжения постоянного тока соответствовала положительному потенциалу на базовом металле.
В качестве измерительной схемы использовался двуплечий дифференциальный мост с параллельной схемой замещения конденсаторной структуры. Для приложения постоянного смещения последовательно с генератором переменного сигнала подключался источник напряжения постоянного тока, шунтированный конденсатором большой емкости, Измерения о (и)) при повышенной температуре производились с использованием герметичной электролитической ячейки,
Исходя из полученных данных для каждой температуры определялась граничная частота, на которой частотная зависимость 0(to)при наличии постоянного смещающего напряжения совпадает с частотной зависимостыо проводимости без приложения постоянного смещающего напряжения: (tk, и Ш0 (см.чертеж). Как видно из чертежа, с увеличением температуры граничная частота возрастает, что соответствует электронным
переходам с участием фононов и отвечает совокупности данных по процессам переноса заряда в анодном оксиде тантала.
Полученный результат позволили сделать вывод о наличии в а TaaOs сильной электрон-фононной связи, на основании чего были указаны пути уменьшения проводимости аморфного диэлектрика посредством его структурной релаксации. Используемые
для этого технологические приемы формирования окисла позволили существенно уменьшить токи утечки оксидных конденсаторов и повысить их надежность.
Отметим, что использование способапрототипа (как и аналогов) тип электронных переходов определять не позволяет.
К достоинствам предлагаемого способа следует отнести применимость к широкому классу неупорядоченных неметаллических
материалов, включая технические диэлектрики и полупроводники, возможности исследования электрических свойств которых остаются весьма ограниченными; информативность в отношении механизма электропроводности в сильных электрических полях; нерззрушающий характер, что гарантирует неизменность кинематических свойств анализируемого материала в процессе измерения; наличие необходимой для
измерений аппаратуры.
Способ определения прыжковой электропроводности в неупорядоченных неметаллических материалах позволяет оперативно контролировать влияние условий
формирования (технологических факторов) и нагружения на кинетические процессы в материале, определяющие его функциональные свойства в полупроводниковых и диэлектрических приборах.
Формула изобретения
Способ определения прыжковой электропроводности в неупорядоченных неметаллических материалах, включающий измерение частотной зависимости малосигнальной проводимости на переменном токе при различных температурах, отличающийся тем, что, с целью осуществления возможности определения типа электронных переходов прыжковой электропроводности, при каждой температуре к об- разцу дополнительно прикладывают постоянное смещающее напряжение, величина которого лежит в интервале, соответствующем падению проводимости на постоянном токе с ростом напряжения, и
дополнительно измеряют частотную зависимость малосигнальной проводимости при наличии постоянного смещающего напряжения, определяют граничную частоту,
наличия с которой частотная зависимость сметающего напряжения совпадает с частотной зависимостью проводимости без приложения постоянного смещающего напряжения, и о типе электронных переходов
судят по направлению сдвига граничной частоты с увеличением температуры.

| Брыскин В.В | |||
| и др | |||
| Прыжковый перенос в некристаллическом окисле тантала.-ФРГ, 1980, т.22,в5, с | |||
| Резервуар для керосиновых ламп типа "Примус" | 1924 |
|
SU1403A1 |
| Звягин И.П | |||
| Кинематические явления в неупорядоченных полупроводниках | |||
| Изд.МГУ, 1984, гл-IV, с.106-135. | |||
Авторы
Даты
1993-05-07—Публикация
1990-10-01—Подача