1
Изобретение относится к области вычислительной техники и может применяться в цифровых интегрирующих машинах.
Известен числовой функциональный .преобразователь типа «приращение - приращение. .содержащий линейные преобразователи «приращение- приращение, реверсивный счетчкк приращения аргумента, дещифратор, схемы сборки и ключи.
Недостатком известного устройства является ,нев0|31можность реализации произвольной функции, задапной графически или таблично, и сложность настройки на отрабатываемую функцию.
Цель Изобретения - достижение возможности реализации функций, заданных графически или таблично, упрощение конструкции и упрощение настройки на требуемую функцию.
Для достижения этого предлагаемый преобразователь дополнительно содержит запоминающее устройство знаков приращения наклонов и реверсивный счетчик приращения наклонов; один вход запоминающего устройства подключен к выходу |ревер|0ивного счетчика приращения аргумента, а другой-к выходу вентиля, выход запоминающего устройства через схему формирования знака приращения наклонов соединен с управляющим входом реверсивного счетчика приращения наклонов, счетный вход которого через линию задержки подключен к
выходу вентиля; выходы реверсивного счетчика приращения наклонов соединены соответственно со входами линейного преОбразователя и входом схемы формирования знака приращения функции, второй вход которой соединен с первым входом реверсивного счетчика приращения аргумента; второй вход реверсивного счетчика лриращения аргумента через вторую линию задержки соединен со входом вентиля, второй вход которого соединен с выходами реверсивного счетчика приращения аргумента.
На фиг. 1 представлена блок-схема универсального числового функционального преобразователя типа «приращение - ириращение ; фиг. 2, 3, 4 иоясняют его работу.
Преобразователь содержит реверсивный счетчик У приращен.ия аргумента Ах, одноразрядное запоминающее устройство 2, линии задержки 3 и 4, реверсивный счетчик 5 приращения наклонов, линейный преобразователь 6, схему 7 формирования знака приращения функции, вентиль 8, схему 9 формирования знака приращения наклона.
В преобразователе применен метод кусочнолинейной аппроксимации заданной непрерывной кривой. Такая аппроксимация может быть осуществлена с любой наперед заданной точностью, определяющей количество линейных отрезков.
В преобразователе весь диапазон изменения аргумента х разбит на 2п+т (приращений Ах. Количество приращений в каждом линейном отрезке равно 2, а количество линейных отрезков равно 2. При достаточно большом п полрешность .кусочно-линейной ап.про«симации достаточно мала.
Помимо кусочно-линейной аппроксимации в преобразователе применена ступенчатая алпро;кси.мация каждого линейного отрез-ка, обеспечивающая квантование по независимой и зависимой переменным (фиг. 2).
При этом входная информация - приращения Ал: - представляется в импульсной форме (наличие Емлульса соответствует наличию приращения, а отсутствие импульса-отсутствию приращения), выходная информация - приращения функции - представляется в форме единичных или нулевых потенциалов, соответствующих наличию или отсутствию приращений функции. Наличие ступеньки у ступенчатой кривой (фиг. 2) трактуется как приращение функции и реализуется единичным потенциалом на выходе преобразователя, а отсутствие ступеньки трактуется как отсутствие приращения функции и реализуется нулевым потенциалом.
Система импульсов, соответствующая приращениям аргумента, и система потенциалов, соответствующая приращениям функции, .построенные для кривой на фиг. 2, представлены на фиг. 3.
Преобразователь отрабатывает функции, масщтабированные та.к, что наклон их по модулю не лревыщает . Поэтому число возможных наклонов линейных отрезков Oinределяется числом приращений Дл: в линейном отрезке. Таким образом, возможный наклон линейного отрезка можно представить в форме , где а .принимает любое из значений О, 1, 2..., (.2™-).
Кусочно-линейная аппроксимация, используемая в преобразователе, несколько необыч на. В соответствии с этой аппроксимацией наклон каждого линейного отрезка отличается от наклона соседнего на минимально возможную величину , так что соседние отрезки не .могут иметь одинаковый наклон. Этот способ требует хранения одноразрядных приращений наклонов отрезков вместо .многоразрядных наклонов, что резко снижает объем запоминающего устройства.
Преобразователь работает следующим образом.
Реверсивный счетчик / приращения аргумента Дл; при Поступлении на его счетный вход 10 И1М1пульса Дх и на упра.вляющий вход /:/ потенциала знака приращения аргумента Длгзн формирует число .XiXo, рав.ное числу импульсов или приращений Ал:, отсчитанных от «ачала линейного отрезка.
При переполнении, т. е. при окончании очередного линейного отрезка, формируется импульс, поступающий на запоминающее устройство 2 на вход 12, и формируется номер очередного отрабатываемого линейного отрезка. В качестве считывающего используется импульс, выработанный вентилем 8, открытым в начале линейного отреака, т. е. при
нулевом состоянии счетчика 1, .и про.пускающим на выход импульс Дл:, задержанный линией задержки 3 на время о.кончания переходных процессов в счетчике /. Этот импульс поступает на вход 13 запоминающего устройст.ва 2.
Запоминающее устройство выдает знак пр.иращения наклона очередного отрезка Да Действительный знак приращения на.клона Дозп формируется с помощью схемы 9, имеющей структуру, определяемую формулой:
Дязн Даз„ Дл;з„ V Д«зн ДАГзнЗнак приращения на.клона, выработанный схемой 9, поступает на управляющий вход J4
реверсивного счетчика б приращения накло-. нов, на счетный вход 15 этого же счетчика поступает считывающий импульс, задержанный линией задерж.ки 4 на время окончания переходных процессов в запоминающем устройстве. Та.ким образом, в счетчике 5 форм.ируется .величина наклона очередного отрабатываемого линейного отрез.ка.
Отличительной особенностью счетчика 5 по сравнению с обычными реверсивными счетчиками я.вляется то, что он работает в прямом коде. Для этого в счетчике помимо цифровых разрядов предусматривается знаковый разряд, любое изменение состояния которого используется для сброса в нуль всех цифровых
разрядов счетчика за исключением младщего. Кроме тото, знаки П)р.иращений наклонов, хранимые в заПОМИнаю.Щем устройстве, для отрицательных наклонов берутся обратными. Таким образом, при последовательном уменьшении наклонов в счетчике вслед за нулем 0.0 ...000 сфор1мируетс.я отрицательная единица 1.0...001 в прямом коде. Поскольку, начиная с этого момента, наклоны становятся отрицательными и .кодирование знаков приращений
на.клонов в запоминающем устройстве меняется на обратное, то при .да.льнейщ&м уменьщении наклонов в счетчике фиксируются числа 1.0...010, 1.0...011, т. е. отрицательные двойка, тройка и т. д. При увеличении наклонов в счетчике, например, после отрицательной двойки 1.0....040 фиксируется отрицательная единица 1.0...001 и далее нуль 1.0...000. Вслед за нулем в счетч.ике зафиксируется .положительная единица 0.0...001.
Таким образом, в счетчике 5 формируется в прямом «оде величина наклона отрабатываемого линейного отрезка, т. е. .модуль наклона а .... и знак наклона Озн. 3|Нак Наклона Сзи И знак триращения аргумента Дхзи используются схемой 7 для формировани.я знака приращения функции. Структурная формула схемы 7 имеет следующий очевидный вид:
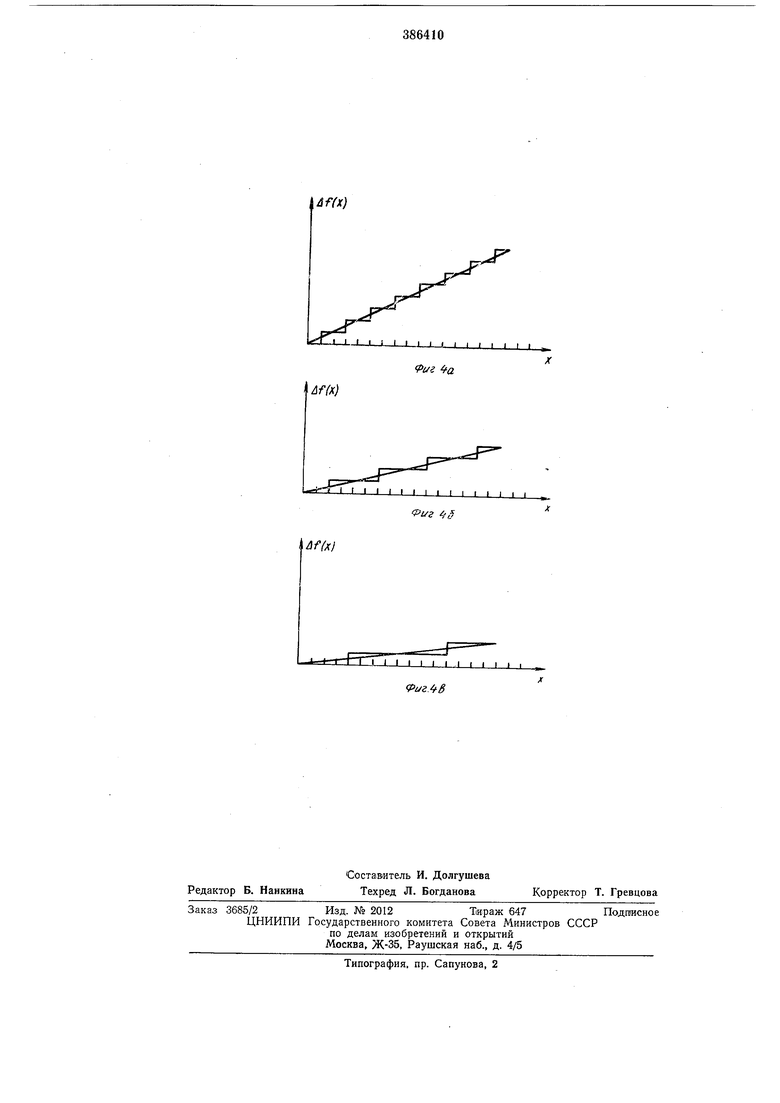
f (Л:)эн «знА- зн / «знД- знМодуль наклона линейного отрезка ... и число --XiXo, содвржащвеся в счетчике / приращения аргумента и равное количеству -приращений Ах, отсчлтанных от начала линейного отрезха, .используются линейным преобразователем 6, выра-батывающим единичный или нулевой потенциал, соответствующий наличию или отсутствию прлращения функции A.f(x) в точке ...XiXo линейного отрезка, имеющего наклон а 0-1.... . Структурная формула линейного преобразователя может быть установлена в результате следующих рассуждений. Представим число , а) ... а-т в форме 0 0-1-0,10...00 +0-2-0,010...00 +... + -(-о-т-0,0....01, ЧТО соответствует представлению наклона о некоторого отрезка суммой наклонов 0,10...00, 0000, 00...01 отрезков, которые можно назвать основными. Рассмотрим основные отрезки и ступенчатые кривые, соответствующие им (фиг. 4 для случая ). В частности, наклону 0,100...00 соответствует ступенчатая кривая фиг. 4а, где (x): во всех точках, где аргумент х представляется числом с . Поэтому функция- Д/ (х) может быть представлена в форме Д/(л) дго. Наклону 0,010...000 соответствует ступенчатая кривая фиг. 46, где Af(x) l во всех точках, где аргумент х представляется числом, у которого . Поэтому функция Af(x) может быть представлена в форме Af() . Аналогичные рассуждения позволяют утверждать, что наклону ,0 ... ОгО.,.0 соответствует логическая функция Д/(л:) y.i xi-iXi-2.. .х JCeИсходя из возможности .представления любого возможного наклона суммой основных наклонов и учитывая, что ступеньки ступенчатых кривых основных отрез.ков не могут накладываться одна на другую, логическая функция, соответствующая отрезку с произвольным наклоном , 0-2а-т может быть представлена в форме: Д/(л:) V V а-2 V V , Х V /Cl-i Xi-lXi-2Х Хо / V -rnXni-l Хт-2Xj X(j . Эта формула является структурной формулой линейного преобразователя. Построенный в соответствии с этой формулой линейный преобразователь чрезвычайно .прост и включает в себя т -1 инвертор, т схем совпадения и одну схему сборки. Предмет изобретения Универсальный ч.исловой функциональный преобразователь типа «приращение - приращение, содержащий реверсивный счетчик приращения аргумента, выходы которого соединены со входами линейного .преобразователя, схему фор.мирования знака приращения наклона, схему форм.ирования знака приращения функции, линии задержки и вентиль, отличающийся тем, что, с целью расщирения функциональных возможностей и со.кращения оборудования, он дополнительно содержит запоминающее устройство знаков приращения наклонов и реверсивный счетчик приращения наклонов, один вход запоминающего устройства подключен к выходу реверсивного счетчика приращения аргумента, а другой - к выходу вентиля, выход запоминающего устройства через схему Формирования знака приращения наклонов соединен с уиравляющим входом реверсивного счетчика -приращения наклонов, счетный вход которого через линию задержки .подключен к выходу вентиля, выходы реверсивного счетчика приращения наклонов соединены соответственно со входами линейного преобразователя и входо.м схемы формирования знака приращения функции, второй вход 1кото рой соединен с первым входом реверсивного счетчика приращения аргумента, второй вход реверсивного счетчика приращения аргумента через вторую линию задержки соединен со входом вентиля, второй вход которого соединен с выходами реверсивного счетчика приращения аргумента.
fM


| название | год | авторы | номер документа |
|---|---|---|---|
| ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ ТИПА «ПРИРАЩЕНИЕ-ПРИРАЩЕНИЕ» | 1973 |
|
SU368618A1 |
| ЦИФРОВОЙ ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ ТИПА ПРИРАЩЕНИЕ — ПРИРАЩЕНИЕ | 1968 |
|
SU208349A1 |
| УНИВЕРСАЛЬНЫЙ ЧИСЛОВОЙФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ ТИПАПРИРАЩЕНИЕ-ПРИРАЩЕНИЕ | 1971 |
|
SU428413A1 |
| Цифровой функциональный преобразователь | 1972 |
|
SU454544A1 |
| ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ АНАЛОГ—ЦИФРА | 1973 |
|
SU388361A1 |
| Синусно-косинусный функциональный преобразователь | 1974 |
|
SU510717A1 |
| Устройство для генерирования функций | 1979 |
|
SU851424A1 |
| ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР | 1973 |
|
SU389519A1 |
| Число-импульсный функциональный преобразователь | 1979 |
|
SU860071A1 |
| Функциональный преобразователь | 1982 |
|
SU1037272A1 |


I I I I I I I I I I I I I I I I I I I I I I I I I I I I И I
uf(K}
I П П П П П П ri n П П П
i I II
-i-I I I I I I I I
Авторы
Даты
1973-01-01—Публикация