1
Изобретение относится к области автоматики и вычислительной техники и предназначено для использования в качестве элемента памяти с большим числом устойчивых состояний в счетчиках импульсов и многозначных запоминающих устройствах.
Известны многостабильные триггеры с п устойчивыми состояниями, содержащие п каскадов, каждый из которых выполнен на элементе «ИЛИ-НЕ («И-НЕ). Выход каждого каскада соединен с входами всех остальных каскадов.
Сложность таких триггеров резко возрастает с увеличением требуемого числа состояний, а нагрузочные характеристики каскадов ухудшаются.
Предлагаемое устройство имеет п каскадов. Его i-й каскад соединен с А-м каскадом, а () (по модулю п) каскад - с (k+w)-M. (по модулю п) каскадом (w, 2,...,п-1).
Особенностью его является то, что в нем каждый каскад соединен с s другими каскадами ( - 2).
Это позволяет упростить устройство за счет уменьшения числа связей между каскадами, упростить схему каждого каскада и увеличить число Л устойчивых состояний до величины , где ,
0,7я-4
S, если ,17rt-f2 0,17я + 2 0,7п -4
(п - s), 0,83п -2
если s50,17rt + 2
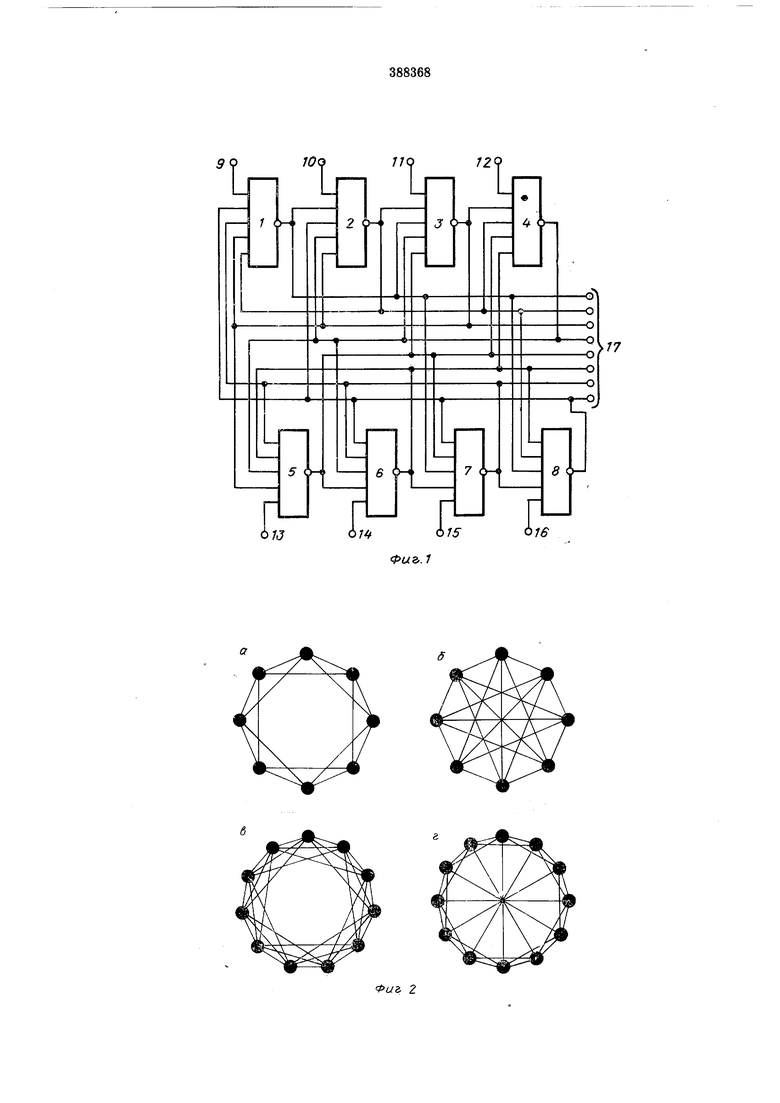
На фиг. 1 показана схема восьмикаскадного триггера с двенадцатью устойчивыми состояниями; на фиг. 2, а-г - структурные схемы триггеров с увеличенным числом состояний; на фиг. 3 - структурные схемы триггеров, построенных на трехвходовых каскадах. Восьмикаскадный триггер содержит элементы «ИЛИ-НЕ 1-8 (вместо них можно
использовать также элементы «И-НЕ, «И-
ИЛИ-НЕ), соответствующие разрядам А-
Я. 9-16 - входы установки, 17 - выходы.
На фиг. 2 и 3 каскады условно изображены
кружками; вместо двух встречных стрелок между соединенными каскадами в структурных схемах для простоты показано одно неориентированное ребро, а входы установки и выходы не показаны.
Сигнал на выходе каждого из каскадов может принимать одно из двух значений - «О или «1.
Каждое устойчивое состояние триггера записывается в виде двоичного числа, i-й разряд которого указывает состояние г-го каскада.
Рассмотрим устойчивые состояния триггера, изображенного на фиг. 1, выполненного по структурной схеме фиг. 2, а.
Пусть в исходном состоянии элемент «ИЛИ-НЕ / находится в состоянии «1 (т. е. Л 1). Сигнал с выхода этого каскада поступает на один из входов каскадав элементов «ИЛИ-НЕ 2, 5, 7 и 8, поэтому последние принимают состояние «О. Любой из оставшихся элементов «ИЛИ-НЕ --4, 5, 6 (разряды Д Е, F) может иметь состояние «1. В случае этот сигнал подается на входы каскадов элементов «ИЛИ-НЕ 5 и 6, в связи с этим последние переводятся в состояние «О. Сигнал также поступает на входы каскадов элементов «ИЛИ-НЕ 2 и 3, но они уже находятся в состоянии «О. Таким образом, и B , т. е. устойчивое состояние триггера описывается кодом 10010000. Точно также возможны еще следующие состояния: 01001000, 00100100, 00010010, 00001001, 10000100, 01000010, 00100001. Они образуют цикл, который для простоты можно записать в виде (10010000).
В другом случае, когда , возможны четыре устойчивых состояния, образующие цикл (10001000). Всего в триггере возможны 12 состояний, каждое из них определяется двумя единицами.
Для установки этого триггера в нужное состояние, например 10010000, на входы 9-16 необходимо подавать сигналы 01101111 соответственно, т. е. инверсии сигналов требуемого состояния. Носле снятия сигналов с входов это состояние сохраняется до поступления других входных сигналов.
С увеличением числа каскадов п максимальное число состояний Ломаке также увеличивается. Оно определяется по формуле
- /макс
где
0,44а - 3 р„акс 0,7л - 5.
Так триггер, структурная схема которого изображена на фиг. 2, б, имеет 20 состояний, т. е. (1010000000) и (1001000000); на фиг. 2,6 - 22, т. е. (10001000000) и (10000100000); на фиг. 2, г -28, т. е. (100100010000), (100010010000) и (100010001000) и т. д. В схемах с максимальным числом состояний выход каждого каскада соединен с sm другими каскадами, где
sm - целое число в пределах 0,167ft-fl ,25rt+4.
Наименьщее число состояний равно наименьщему делителю числа п, превышающему
1, т. е. при (k 2, 3, 4,...) //мин 2, при
(k - нечетные числа) и т. д.,
если п - простое число, например 2, 3, 5, 7,
П,..., то .
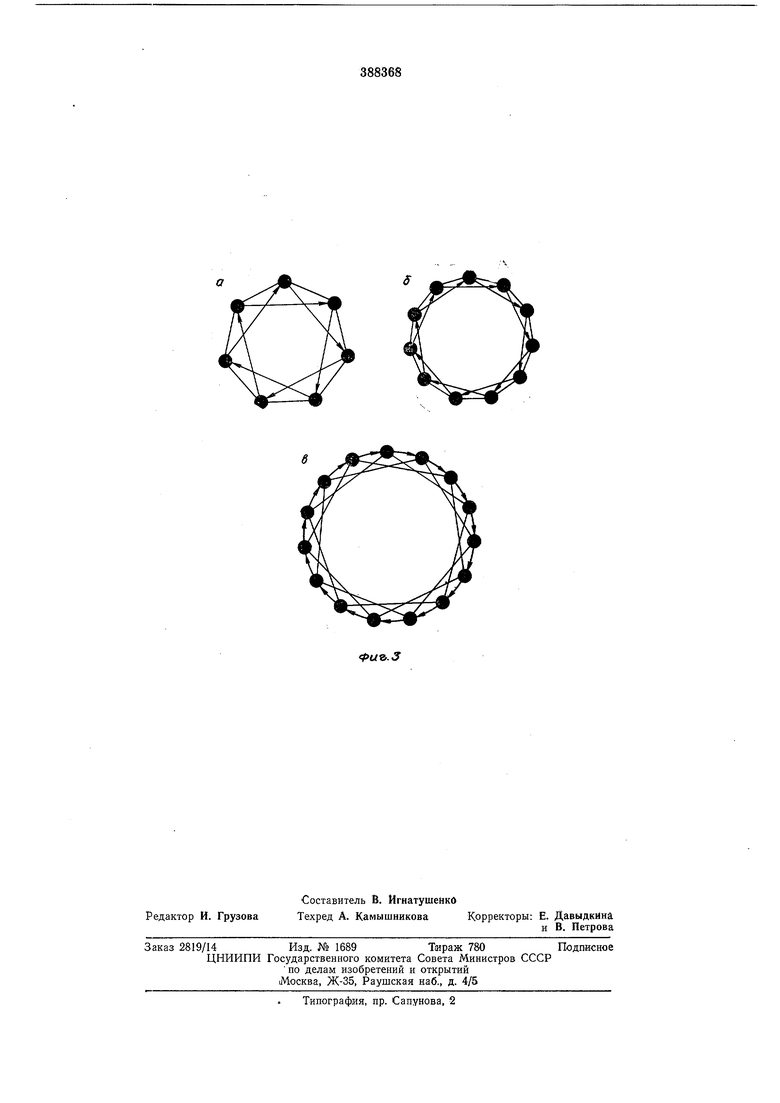
В триггерах с числом состояний, равным числу каскадов (), должно вьщолняться условие при любом . Другими словами, такие триггеры можно построить на трехвходовых каскадах (фиг. 3). Например, триггер, структурная схема которого изображена на фиг. 3, а, имеет цикл состояний (1001000); на фиг. 3, б-(10010010000) на фиг. 3,в- (101010101010100).
В общем случае устойчивые состояния триггера по заданной структурной схеме определяются следующим образом. В соответствии со схемой составляется система уравнений алгебры логики
ЛГА (хг,лг,л;г,...) + й( + h + xj,-{-,..)-l k-l, 2,..., п; i, j, Е{1, 2,..., п},
где Xk, Xi, Xj - переменные алгебры логики, соответствующие выходным сигналам k-, i- и /-ГО каскадов;
й iz, is, -- номера тех каскадов, выходы
которых соединены с входами /г-го каскада;
/ь /2, /3, -номера тех каскадов, один из
входов которых присоединен к выходу k-ro
каскада.
Решения этой системы уравнений представляют устойчивые состояния триггера по данной схеме. Если же система не имеет решений, то заданная схема не является схемой триггера.
Триггер, построенный по одной и той же структурной схеме на различных элементах - «ИЛИ-НЕ, «И-ИЛИ-НЕ и «И-НЕ, в каждом устойчивом состоянии имеет v, (о+ -}-1)(п - V--1) и п-V единиц соответственно.
,-,
Предмет изобретения
Многостабильный триггер, содержащий п каскадов, каждый из которых выполнен на элементе «ИЛИ-НЕ, /-и каскад соединен с
k-M каскадом, а (1+да)-й (по модулю п) каскад соединен с ()-M (по модулю п) каскадом (w, 2,...,п-1), отличающийся тем, что, с целью упрощения устройства и увеличения числа его устойчивых состояний, каждый каскад соединен с s другими каскадами ().
L
L
iL
72
-o
Ч) Ч)
I7
-o -o -o

| название | год | авторы | номер документа |
|---|---|---|---|
| МНОГОСТАБИЛЬНЫЙ ТРИГГЕР | 1972 |
|
SU350183A1 |
| МАТРИЧНЫЙ КОММУТАТОР С ПРОГРАММИРУЕМОЙ ЛОГИКОЙ | 2003 |
|
RU2251792C2 |
| Устройство для вычисления логических производных многозначных данных | 1990 |
|
SU1837277A1 |
| Устройство для умножения элементов конечного поля GF(2 @ ) при м @ 3 | 1990 |
|
SU1728858A1 |
| Устройство для отбора @ ядерных частиц | 1987 |
|
SU1497597A1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2020 |
|
RU2751802C1 |
| Устройство для воспроизведения симметричных функций нескольких переменных | 1984 |
|
SU1226493A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1474671A1 |
| Устройство для замера наименьшего диаметра бревен | 1978 |
|
SU750253A1 |
| Устройство для контроля цифровых блоков | 1985 |
|
SU1288700A1 |

5 6-«
67J
7 6-
9 9
6 Ф-
с
75076
Фиъ. 1
Авторы
Даты
1973-01-01—Публикация