Наиболее рациональной формой кривой электродвижущей силы у альтернатора считается синусоида; при конструировании динамо-машин стремятся к тому, чтобы электродвижущая сила альтернатора по крайней мере в разомкнутом состоянии возможно ближе подходила к гармонической кривой. Но форма кривой электродвижущей силы тесно связана с формой кривой магнитного поля машины, а также с формой катушек якорной обмотки. Между тем кривая поля, при обычном начертании полюсного наконечника, близкая к форме прямоугольника, не удовлетворяет этому условию: при простой форме катушек с одним каналом на полюс и фазу и с шириной катушки, равной полюсному делению, кривая электродвижущей силы будет тождественной с кривой поля. Размещение стороны катушки в нескольких каналах, или применение непрерывно распределенной обмотки, уменьшает этот недостаток, сглаживая угловатую форму кривой электродвижущей силы, но никогда не достигается совершенного результата.
Отсюда возникает вопрос о наиболее рациональной форме кривой магнитного поля машины. На первый взгляд казалось бы, что прямоугольная форма имеет преимущество, так как обнимает наибольшую площадь, т.-е. дает наибольший поток при данном размере междужелезного промежутка, обеспечивает большую величину электродвижущей силы и тем позволяет с′экономить на меди. Однако, более глубокое изучение вопроса показывает, что и для поля альтернатора единственно рациональной формой является синусоида. Это заключение выводится непосредственно из разложения кривой поля на гармонические составляющие: всякое отклонение кривой поля от синусоиды выражается прибавкой к основной гармонической кривой целого ряда гармоник высшей периодичности, которые будут индуктировать в обмотке статора переменные токи большой частоты. Токи эти, благодаря сильному действию самоиндукции от потока утечки при высокой периодичности, будут отставать от вызвавших их электродвижущих сил почти на четверть своего периода, а от индуктировавших их волн потока будут разниться в фазе примерно на 180°; этот результат приводит к почти полному аннулированию, всех высших гармоник кривой поля. Таким образом, всякая добавка к синусоидальному полю пропадает без пользы для электродвижущей силы машины, напротив, она создает только лишние потери от токов высокой периодичности в обмотке статора. Согласно Арнольду полюсным наконечникам следует придавать такую форму, чтобы кривая поля возможно ближе примыкала к синусоиде и чтобы верхняя часть кривой не была сглажена.
Отсюда понятно стремление изменить кривую поля, отклоняя ее от прямоугольной формы в сторону синусоиды. Некоторое улучшение в этом направлении достигается относительным увеличением междужелезного промежутка δ, отчего углы кривой поля округляются, но это получается ценой повышения возбуждающих ампер-витков. Некоторые фирмы применяют полюсные башмаки со скошенными сторонами (фиг. 1), благодаря чему проводники постепенно погружаются в более сильный поток и результат получается такой, как будто поле своей формой приближалось к трапеции. Ту же цель - приближение кривой поля к синусоиде - Арнольд рекомендует осуществлять особой формой полюсного наконечника (фиг. 2); общая ширина его делается равной 0,667 полюсного деления τ, средняя его часть шириной 0,31 τ очерчивается концентрично со статором, а края скашиваются настолько, чтобы здесь ширина, междужелезного промежутка δ1 составляла около 1,5 δ т.-е. промежутка в концентричной части. Наконец, полюсный башмак, вместо концентричной дуги на всей ширине, очерчивается дугой круга, меньшего радиуса (фиг. 3). На фиг. 1, 2 и 3 для каждой кривой поля помещена основная синусоида, от которой отклонения, как видно ясно, выражаются гармониками 3 и 5 порядков, а также, конечно, и более высокими.
Однако, все здесь указанные и иные применяющиеся в динамостроении средства, представляют только некоторые улучшения формы кривой поля, и, конечно, не в состоянии дать для нее правильную синусоиду.
Есть еще причина, заставляющая стремиться к получению синусоидальной кривой поля. У тщательно разработанного альтернатора кривая электродвижущей силы все же отклоняется от синусоиды, и эти отступления выражаются в том, что на правильную синусоиду накладываются некоторые волны (фестоны, длина которых совпадает с делением зубца якоря) (фиг. 4). Последнее обстоятельство явно указывает, что их происхождение вызвано зубчатой поверхностью якоря, действие которой сводится к следующему. Проводимость трубок индукции по поверхности якоря не одинакова: против зубцов она больше, против пазов значительно ниже; поэтому поток, выходящий из полюса в якорь, будет неодинаков для различных положений зубцов относительно полюса: он будет наибольшим при таком положении, когда сумма ординат кривой поля, взятых против зубцов, окажется наибольшей; наоборот, величина потока примет наименьшее значение, когда указанные ординаты; против пазов якоря дадут наибольшую сумму. При изменении взаимного положения на величину деления зубца относительное положение зубцов и полюса, а отсюда и величина потока будет повторяться. Самостоятельные исследования в этом направлении привели к следующему выводу: периодические колебания потока на длине деления зубца вовсе не будут, если изменение суммы ординат поля, взятых против впадин зубчатого якоря, следует синусоидальному закону. Это будет в том лишь случае, когда сама кривая поля представляет правильную синусоиду.
Между тем присутствие на кривой электродвижущей силы высших гармоник от зубцов, помимо лишних затрат на потери в машине, влечет за собой более существенный недостаток, так как эти гармоники при некоторых условиях дают резонанс в линии, соединенный с опасным повышением напряжения. Можно указать еще на одно ценное преимущество синусоидального поля, основанное на свойстве гармонической кривой: сумма (или разность) смешанных синусоид одной продолжительности периода дает всегда синусоиду. Вследствие этого в синусоидальном поле электродвижущая сила будет синусоидой, независимо от того, будут ли применяться катушки с одним или несколькими каналами на полюс и фазу, с распределенной обмоткой или раздельной, типа постоянного тока.
Решение вопроса о синусоидальной форме кривой поля основывается на теоретических исследованиях, позволяющих выяснить форму башмака, который на протяжении всей ширины полюса будет давать для поля точную синусоиду, а за его краями кривую, близкую к синусоиде. Здесь необходимо будет привести основные положения и конечные выводы.
Распределение поля по поверхности якоря выясняется или путем вычерчивания линий индукции в междужелезном пространстве (способ, не отличающийся точностью), или же вычисляется, как сила взаимодействия между магнитными массами, распределенными по поверхности полюса, а также якоря и единицы массы в данной точке якорной поверхности; последний способ в обычном своем виде отличается крайней сложностью, требуя решения 15-20 уравнений с предварительным вычислением сотен коэффициентов по сложным формулам. В предлагаемых расчетах пользуются принципом последнего метода, придавая, однако, его применению и конечным выводам простейшую форму.
Исходным пунктом является следующий вопрос Дана плоскость А, представляющая развернутую поверхность якоря, и часть ВС, принадлежащая поверхности полюсного башмака (фиг. 5); для любой точки Р поверхности якоря можно говорить об удельной проводимости между поверхностью ВС и якорем, разумея под этим отношение проводимости элементарной трубки в выбранной точке к ее сечению или, что одно и тоже, проводимость трубки с основанием в один квадратный сантиметр в выбранной точке поверхности якоря. Умножая эту проводимость на магнитодвижущую силу для преодоления междужелезного пространства (величина постоянная, значение ее определяется в конце расчета) мы получим магнитную индукцию в точке Р. Если расстояние между ВС и якорем мало сравнительно с его длиной (размер, перпендикулярный к плоскости чертежа), то для удельной проводимости γ, на основании исследований, получается выражение

здесь α есть угол наклона ВС к якорю,φ угол, под которым из точки Р виден отрезок ВС (оба угла могут быть выражены в градусах) и h есть высота перпендикуляра, опущенного из Р на ВС. Найденные отсюда значения γ для ряда точек и дадут кривую поля между полюсом ВС и якорем. В частном случае, когда полюс состоит из площадки, параллельной якорю (фиг. 6), формула принимает вид

и кривая получает указанную на чертеже форму. Если принять во внимание действие соседних полюсов другого наименования, то получится кривая, обозначенная на фиг. 6 пунктиром.
Всякий наконечник, очерченный кривой линией, можно разбить на ряд прямолинейных отрезков, и тогда проводимость в любой точке якоря найдется, беря сумму выражений 1 для каждого из отрезков.
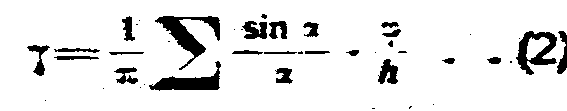
Сумма берется для всех составных элементов наконечника, из которых поток идет в якорь.
Тот же вопрос для криволинейного наконечника решается тем же аналитическим путем. Если дана кривая MN (фиг. 7) полюсного наконечника в форме уравнения ƒ(х, у)=0, то элемент А на его поверхности создаст в точке Р в расстоянии ξ от начала проводимость 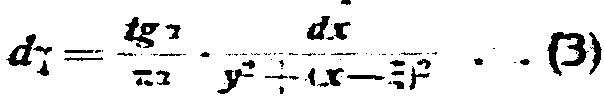
Пользуясь уравнением кривой наконечника, интегрирование выражения (3) определит проводимость для ряда точек якоря и позволит построить кривую поля. На практике приходится ограничиваться лишь такой формой наконечника, когда обращенная к якорю поверхность имеет только небольшой наклон, т.-е. малый угол α. Исследование показывает, что при такой пологой форме кривой наконечника, какой бы линией они не очерчивались, проводимость γ может быть найдена из выражения
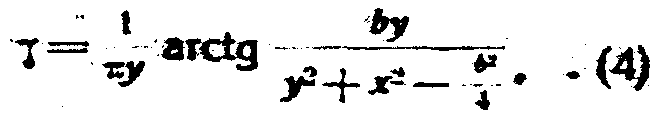
где b ширина полюсного наконечника (фиг. 7).
Наконец, можно поставить обратную задачу: найти уравнение кривой, по которой должен быть очерчен полюсный наконечник, чтобы он создал для поверхности якоря проводимость по синусоиде. Разработанные автором положения дают для этого уравнения следующий вид

Здесь δ есть теоретическая величина междужелезного пространства по оси полюса, а τ - полюсное деление (фиг. 8). Определение из этого уравнения, ординаты y, входящей также под знаком арктангенса, может быть произведено способом последовательных приближений. Форма кривой, ограничивающей наконечник, при данном τ будет меняться вместе с шириной полюса b и воздушного промежутка δ. Фиг. 9 дает кривую наконечника для τ=24, δ=1 и b=18 см; кривая в средней своей части обращена, к якорю своей выпуклостью, а у краев вогнутостью, давая в промежутке точку перегиба. На фиг. 10 представлена кривая для меньшего воздушного промежутка δ=0,5 и b=16 см; форма ее, сохраняя в общем прежний характер, является менее углубленной. Увеличение ширины полюса при том же значении δ (фиг. 11) отодвигает к краю точку перегиба и вместе с тем увеличивает высоту ординаты под краем наконечника. Дальнейшее увеличение ширины b дает на всем протяжении полюса выпуклую кривую (фиг. 12). Для заданных τ, δ и b вычисление ординаты у для принятых значений абсциссы х с любой степенью точности производится по уравнению 5. При определении таким путем формы кривой полюсного наконечника для проводимости по поверхности якоря или, что одно и тоже, для кривой поля получится точная синусоида на всем протяжении ширины b полюса, а также на некотором расстоянии за краем его, и только вблизи нейтральной линии поле будет незначительно отклоняться от синусоиды, образуя здесь несколько более быстрое падение.
Разработанный метод дает возможность сгладить и это отклонение от синусоиды, делая на гранях наконечника плоский обрез с некоторою высотою h1 нормально к поверхности якоря: выходящие отсюда линии индукции будут увеличивать поле за краем наконечника более значительно нежели сгущать их у края под самым наконечником - последнее же усиление поля может быть учтено расчетом. Кривая на фиг. 13 иллюстрирует влияние обреза h1=2,5 см для наконечника, изображенного на фиг. 10.
Вычерченная по координатам х и у кривая наконечника дает его форму для развернутого в плоскость якоря, а для действительной, т.-е. цилиндрической поверхности абсциссы х будет представлять расстояние по дуге круга от оси полюса (фиг. 14), ордината же у - ее расстояние от этой дуги по радиусу. Для выяснения ее действительной формы в прямоугольных координатах х′ и у′ остается сделать переход к ним от координат х и у. Это преобразование для наконечника, изображенного на фиг. 13, сделано на фиг. 14; вместе с тем здесь произведено закругление кромки наконечника, чтобы избежать некоторого сгущения линий индукции около острого края.
Для междужелезного пространства δ может быть взята возможно малая величина, допускаемая условиями конструкции. Ширину же полюса можно брать более обычно применяемой, с целью получения на возможно большем протяжении строго синусоидального распределения потока. Повышающаяся от этого утечка не повлечет за собой увеличения расхода на возбуждение, так как значительная ширина полюса и малая величина δ сильно увеличивают общую проводимость через воздушную щель, отчего расход на возбуждение будет даже понижен. Применение криволинейного башмака с целью получения синусоидального поля не может ограничиться одними машинами переменного тока. При обычной конструкции машин постоянного тока применяется относительно узкая воздушная щель, что обусловливает резко прямоугольный характер поля с сильным ослаблением его у нейтральной линии; этим создаются неблагоприятные условия для коммутирования тока в полосе нейтральной зоны. Применение здесь башмаков с синусоидальным полем повысит его величину в полосе коммутирования и создаст более благоприятные условия для работы без искрения.
Предлагаемый наконечник, осуществляющий синусоидальное поле, может быть очерчен как непрерывной кривой, так и рядом прямолинейных отрезков, близко примыкающих к этой кривой.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для выравнивания продольного и поперечного полей многофазной синхронной машины | 1920 |
|
SU11025A1 |
| Синхронная электрическая машина | 1988 |
|
SU1525812A1 |
| Генератор переменного тока | 1938 |
|
SU69549A1 |
| Явнополюсная синхронная электрическая машина | 1986 |
|
SU1403228A1 |
| НИЗКОСКОРОСТНАЯ ЭЛЕКТРИЧЕСКАЯ МАШИНА С КОЛЬЦЕВЫМ СТАТОРОМ | 2009 |
|
RU2417506C2 |
| Импульсный синхронный генератор | 1952 |
|
SU95095A1 |
| Коллекторная электрическая машина | 1983 |
|
SU1098083A1 |
| ЭЛЕКТРИЧЕСКАЯ РЕДУКТОРНАЯ МАШИНА С ПОЛЮСНЫМ ЗУБЧАТЫМ ИНДУКТОРОМ | 2009 |
|
RU2393614C1 |
| Полюс явнополюсной синхронной электрической машины | 1987 |
|
SU1436189A1 |
| Ротор звездообразного типа | 1989 |
|
SU1674324A1 |

Полюсный башмак электрических машин постоянного и переменного тока для синусоидального распределения магнитного потока на поверхности якоря, характеризующийся таким очертанием поверхности башмака, обращенной к якорю, при котором длина между-железного промежутка у (фиг. 14), в какой-либо точке, находящейся на расстоянии х от середины башмака с полюсною дугою, равною b, и полюсным шагом, равным z определяется формулой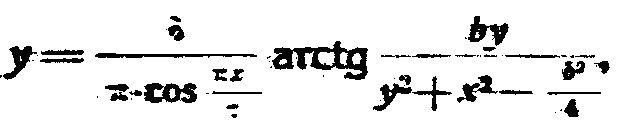
где  - расчетная длина между-железного промежутка, приблизительно равная длине между-железного промежутка под серединою башмака.
- расчетная длина между-железного промежутка, приблизительно равная длине между-железного промежутка под серединою башмака.
Авторы
Даты
1927-12-31—Публикация
1922-06-07—Подача