Изобретение относится к вычислительной технике, а именно к моделированию функции неопределенности радио- и гидролокационных сигналов.
Как известно, функция неопределенности A(Q, т) характеризует потенциальную разрешающую способность зондирующего сигнала одновременно по дальности и скорости цели и является откликом согласованного фильтра или коррелятора на отраженный от точечной цели сигнал U(t), который был подвергнут временному запаздыванию т и доплеровскому смещению и:
Z(Q, ) U(t)U (t т) (1)
- оо
или
оо
Х(и I U(t)U-(t-)X
00
X,(-),(2)
где ср(/)-закон фазовой модуляции зондирующего сигнала.
Вычисление функций неопределенности необходимо для выбора параметров зондирующего сигнала, а также для оценки рабочих характеристик радио- и гидролокаторов с опти.мальной обработкой зондирующего сигнала.
Известный электронно-оптический способ моделирования функции неопределенности, основанный на использовании двух последовательных преобразований Фурье, связан с необходимостью изготовления двух сложных транспарантов сигнала с записью комплексных функций. Он дает возможность получать сечения функции неопределенности только для дискретных значений т и И; трудоемок и требует много времени на изготовление сложных транспарантов сигнала.
Цель изобретения цовыщение точности моделирования функции неопределенности, устраняющего многие недостатки известных когерентных электронно-оптических способов моделирования за счет применения специального транспаранта со щелью и функционально прозрачной маской, и обеспечивающего получение функции неопределенности не при дискретных
значениях т и Q, а при плавно меняющихся. Для достижения поставленной цели на непрозрачный входной транспарант двумерного когерентного электронно-оптического анализатора спектра наносят узкую щель, закон которой воспроизводит закон частотной модуляции исследуемого сигнала, или щель, закон которой воспроизводит функцию
- f(t) +Cf( - TO)
30
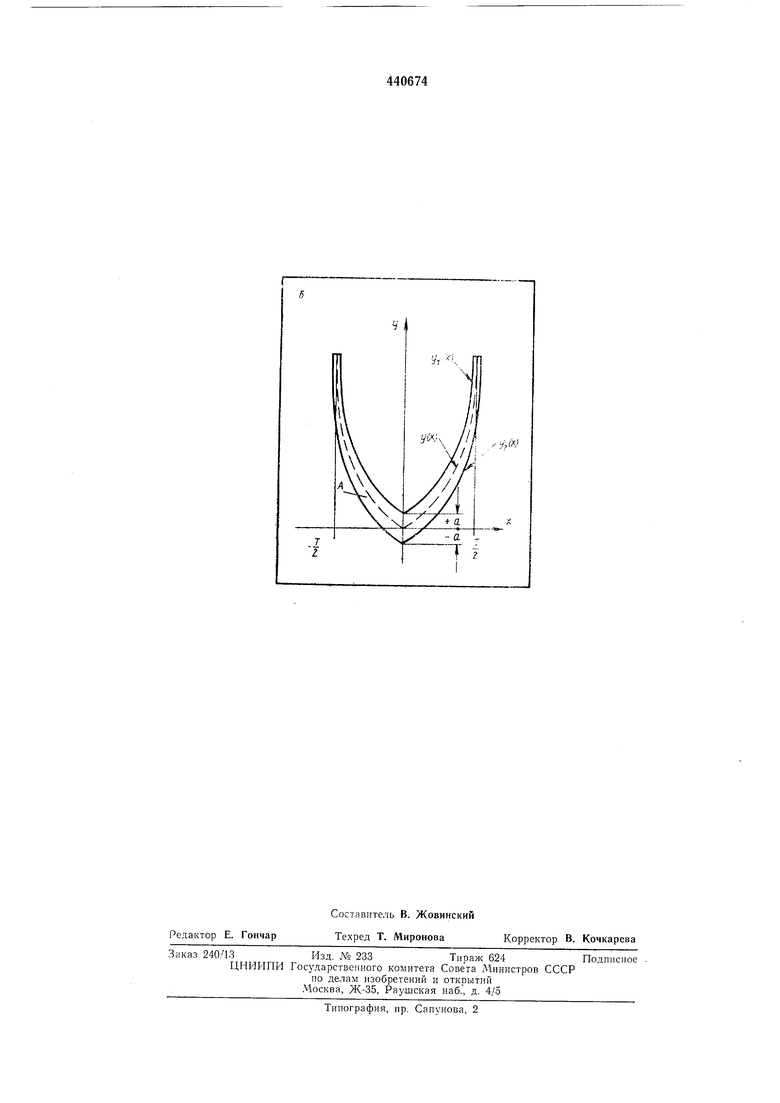
где Tn - требуемое значение задержки т. Двумерный пространственный спектр таких сигналов (щелей) моделирует функцию неопределенности. На чертеже приведен транспарант, выполненный в виде узкой щели, представляющий собой единично-нулевую функдию Р.(..,,) (3) i о (л:, у)-Л Такой транспарант можно выполнить в виде прозрачной щели А в непрозрачном экране Б. Щель А образована путем смещения кривой у(х) по оси ординат на величину ±а. Амплитуда света на щели соответствует единичному значению функции и нуля вне ее. Двумерный спектр транспаранта в области пространственных частот f/ и У дает следующее выражение F(UV)-2a Г (4) Сравним выражение (4) с выражением (2), предварительно положив, что произведение модулей аналогических сигналов равно единицеU(( , т. е. исследуемый сигнал имеет прямоугольную огибающую и модулирован только по фазе (частоте). Переменным J:, f/ и F в выражении (4) припишем соответственно значения переменных t, Q, т выражения (2). . .(6) Теперь сравнение выражений (4) и (2) показывает, что для того, чтобы двумерное преобразование Фурье единично-нулевой функции являлось моделью функции неопределенности, необходимо выполнить равенство показателей степени в экспоненциальных множителях -Кг/(л:).(0-ср(-.)(7) ,Н.(() Таким образом, для того, чтобы двумерный спектр щели являлся моделью функции неопределенности некоторого сигнала, необходимо, чтобы единично-нулевая функция (щель) изменялась в соответствии с вырал ением (8). Как видно из выражения (4), моделирование функции неопределенности выполняется с весовым множителем, вынесенным за знак интеграла. Этот множитель при малых а (бесконечно узкая щель) оказывает незначительное влияние на функцию неопределенности сигнала, так как он стремится к постоянной величине 2а. Поэтому при моделировании щель необходимо выполнять как можно более узкой. Зная щирину а щели, в требуемых случаях можно учесть влияние этого весового множителя. Если член (р(-т)-выражения (8) разложить в ряд Тейлора по производным закона частотной модуляции, то можно построить щель IJ(K), двумерный спектр которой моделирует функцию неопределенности этого сигнала. Если при разложении в ряд Тейлора окажется воз.можным пренебречь членами высшего порядка малости, то форма щели будет повторять закон частотной модуляции. Таким образом, если щель выполнить в виде закона изменения частоты сигнала, то ее двумерный спектр с достаточной степенью точности моделирует функцию неоцределенности этого сигнала для непрерывно изменяющихся значений т и Q. Можно также показать, что для сигналов с огибающей, отличной от прямоугольной, на щелевой транспорант должна быть наложена амплитудная маска, прозрачность которой вдоль щели (по оси) должна изменяться по закону огибающей сигнала. Предмет изобретения Транспарант для когерентного оптического моделирования функции неопределенности модулировочных сигналов в плоскости пространственных частот, выполненный в виде оптически непрозрачной пластины с прозрачной щелью, отличающийся тем, что, с целью повышения точности моделирования, он содержит пластину, оптическая плотность которой функционально задана, размещенную на плоскости непрозрачной пластины, прозрачная щель которой выполнена в соответствии с заданным законом частотной модуляции сигнала.

| название | год | авторы | номер документа |
|---|---|---|---|
| КОГЕРЕНТНЫЙ ОПТИЧЕСКИЙ КОРРЕЛОМЕТРи~ • ^ .г ?? Л Т';V 1"г'i f"« •-:-•••'.-;•..f (^Hk:r! й-;..:'-;.-,;:'• ^'.L. | 1973 |
|
SU377821A1 |
| УСТРОЙСТВО РАДИОЛОКАЦИОННОЙ СТАНЦИИ С НЕПРЕРЫВНЫМ ЛИНЕЙНО-ЧАСТОТНО-МОДУЛИРОВАННЫМ СИГНАЛОМ И СИНТЕЗОМ АПЕРТУРЫ | 2017 |
|
RU2660450C1 |
| СПОСОБ КОРРЕЛЯЦИОННОЙ ОБРАБОТКИ СИГНАЛОВ, ОТРАЖЕННЫХ ОТ БЫСТРОДВИЖУЩИХСЯ ЦЕЛЕЙ | 2005 |
|
RU2293997C1 |
| Устройство оптической обработки информации | 1975 |
|
SU558284A1 |
| Опорный транспарант для акустооптических корреляторов | 1976 |
|
SU605185A1 |
| Акустооптический спектроанализатор с интегрированием во времени | 1990 |
|
SU1837332A1 |
| Способ анализа спектров сигналов | 1979 |
|
SU817601A1 |
| УСТРОЙСТВО КОГЕРЕНТНОЙ ОПТИЧЕСКОЙ ФИЛЬТРАЦИИ | 1971 |
|
SU297058A1 |
| ЛЕКТРОННАЯ ОБУЧАЕМАЯ СИСТЕМА | 1970 |
|
SU278229A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛЬНЫХ | 1969 |
|
SU253454A1 |


Авторы
Даты
1974-08-25—Публикация
1973-02-20—Подача