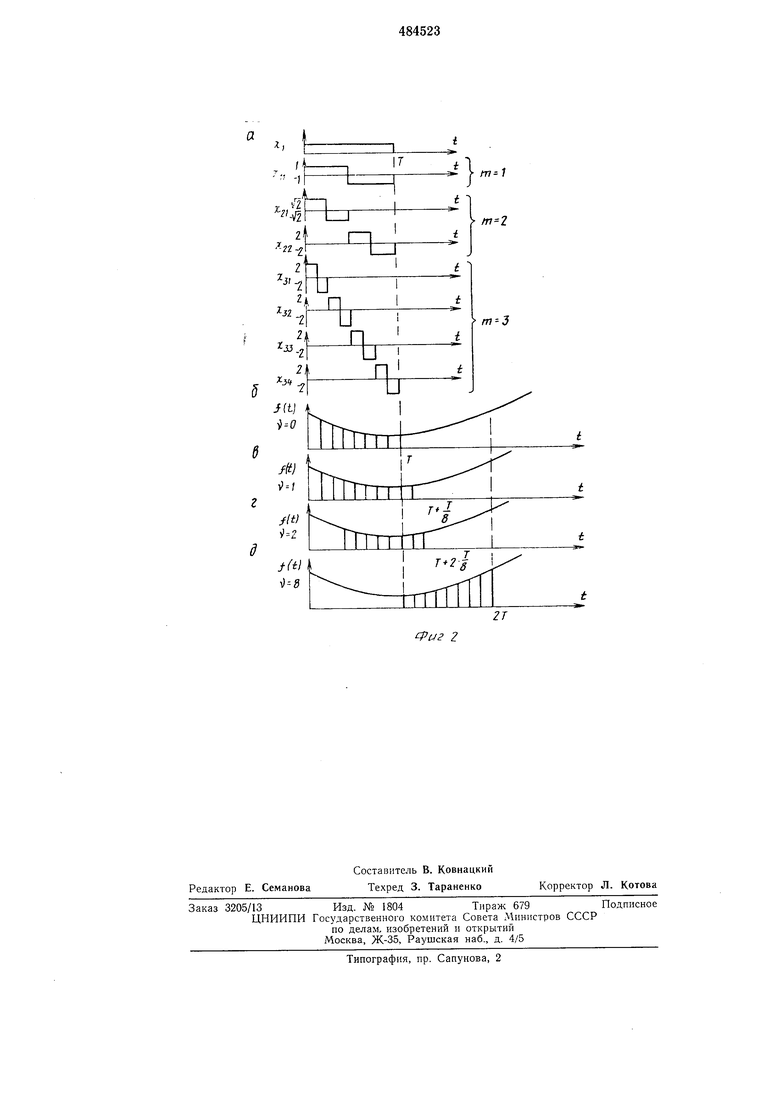
3 причс.м первая функция остается вне группы, функции Хаара имеют вид: , 2 при Х,„,-(0 - 1 -2 - при iQl О при fQl,nj, -( () ()7-JT .)Л - 1 ,„; - /- + / , //гу nij , ,где /- и / -двоичные отрезки, получае мые путем деления отрезка О, Г на 2 равных час-тей. На фиг. 2,а изображены первые восемь функции Хаара. Если функцию f{t) разложить в 1-м интервале в ряд Хаара, то для -го коэффициента получают: Cil) Си (/, Г) - -1 ( f (/) х. (/) d/, т ( 1 О где I -интервал разложения, , , 3,... - текущий номер выбранного интервала. В предлагаемом устройстве для формирования коэффициентов разложения Хаара выдача коэффициентов цроизводится не на интервале О, 7, а на скользящем интервале /о, Г+М, /о меняется с шагом Д/ г- -L .. -1. Для й-го , ,коэффицента на скользящем интервале полу43ют . С/Л/о- +о) - ( f(07.ft( /, Т -; V - 1, 2, 3,- . . , 2 где /По-максимальный номер класса фупкции Хаара, v - номер шага скользящего ий-gg тервала, Г -интервал ортогональности. Коэффициенты Фурье-Хаара для произвольного Т в любой момент определяются по формулам. 55 1 р Т ()) () о о г-( С„,2 | J /(d/- J f(0d m-i I 2 I ГУ у I/2 Т mj mj65 4 Для вычисления ннтеграла /- - J /(Od nij i промежуток интегрирования делится на .V , частей, и к каждому применяется форму-ча транеций. Полагая, что /г -и обозначая через yi l(ti}, (t 0, 1, 2,..., Л ) значения иодынтегральноч функции в точках /,-, будем х , , ,, i.vN Т X + i/, + Уа + . . + -f j --- лГ . J где 5 -сумма ординат функции /(/,) па „,,- - ) двоичном интервале 1-, причем первая и послс,,я ординаты делятся пополам. Формулы j ,2) „о,., записать в другом виде: J.5 5 (З) W m-l С 2 . - S - 5 , J Л „,; mj Hi-1 . 9 1 - Ш- , Из формулы (4) видно, что получение коэффициептов Фурье-Хаара сводится к вычис,„,, разностей приведенных сумм S и S. , соответствующих интегралам от функции ДО на двоичных отрезках / и / - , из фиг. 2,а mj mj видно, что интеграл от функции f(t) на двоичном отрезке младщего класса можно получить путем суммирования интегралов на двоичных отрезках старшего класса. Например: S + S,,. 31 31 32 32 21 21 п Таким образом, достаточно один раз опреде. двоичных отрезках / и U самого m,j старшего класса то интегралы - , S, 6, iV, 5+, 5, б., (5) 2 32 за з4 а по ним вычисляются все необходимые коэффициенты Фурье-Хаара. Для этого необходиМО интегралы (5) сначала разделить на qnCvio шагов Л . Полученные суммы ) 1 -Г 1 -fl 1 31 31 32 32 33 33 34 34 подаются на входы соответствующих сумматоров. с выходов сумматоров, работающих на сложение, получаются числа, используемые ДЛЯ дальпейщих вычислений, а с выходов
сумматоров, работающих на вычитание, получаются коэффициенты Фурье-Хаара. Так:
- -
31
31
-S,-,
Сз2 - -
32
32
Сзз -- 4-,
3333
Сз, - S - S,,
34
34
C,, (S + ,
31313232
с,, 51+5;-(51+ 5.),
33333434
С,, + 5 + 5 31313232
-(5 +5-+5-+5Д
33333434
jz: 5 + 54. +
313132323333
+ ..
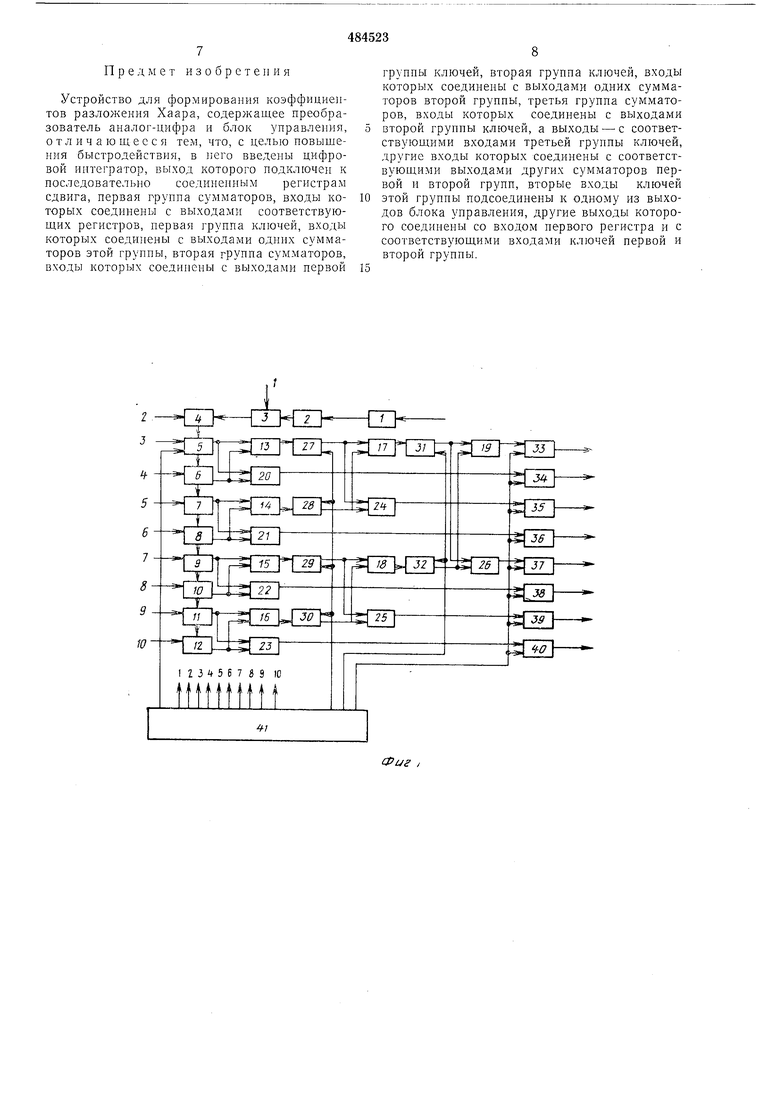
3434 Так как восстановление сигнала по коэффициентам производят на синтезаторах и уииверсальных ЦВМ, то величину 2 можно легко учесть. Таким образом, на выходе получают не коэффициенты Фурье-Хаара, а числа Ci Si, Cmj --- S - 5-, . Устройство работает следующим образом. Цифры, соответствующие отсчетам функции Т f(t), поступают с периодом - через регистр 3 сдвига на сумматор-интегратор 4. В регистре 3 сдвигается на один разряд влево только первое и последнее число соответствующего двоичного отрезка, что соответствует делению на половину. На регистре 5 к моменту времени / -- -фиксируется значение иитеграла 5 , сиимаемое с сумматора-иитегратора 4. Это число сдвигается влево на q разрядов (), что соответствует делению иа .V и получению приведенной суммы. В момент Т 2- значение S переносится из регистра 5 П31 в регистр 6, а в регистр 5 занисывается число, соответствующее интегралу 5-.. . В следующий момент 3 - число из регистра 6 переноситпся в регистр 7, из регистра 5 - в регистр 6, а
В регистр 5 записывается новое значение интеграла S . С исступлением последнего зна32
чения интеграла S+...
34 в регистр о, т. е. в конне
интервала ортогональности Г, нриведенные суммы подаются на сумматоры 13-16 и 20- 26. С выходов сумматоров 13-16 одновременно, все числа иоступают через ключевые элементы 27-30 на входы сумматоров 17 и 18, работающих на сложение, и на сумматоры 24 и 25, работающне на вычитаиие. С выхода сумматоров 17 и 18 числа через ключевые элементы 31 и 32 одновременно подаются на вход
сумматора 19, работающего на сложение, и иа сумматор 26, работающего на вычитание.
Коэффициенты СЗР С , Cgg, Cg, Cjj, Cog, Cjj
снимаются с сумматоров 23, 22, 21, 20, 25, 24 и 26. Первый коэффициент Фурье-Хаара, формируемый иа сумматоре 19, равеи сумме приведенных сумм на всех двоичиых отрезках самого старщего класса /По 3
с; г. S + 5. + S + 5. + 5 +
3131323233
+ 5..-f S + 5l.
333434 Съем всех коэффнциеитов производится одновременно через ключевые э.тементы 33-40. Работу всего устройства сннхроиизирует блок управления 41. На фиг. 2,6 показан момент временн, когда все регистры 5-12 заполнены чнсламн. соответствующими значениям интегралов О5 ---1 + ) 1 ) 1 О.31 31 32 32 33 33 34 34 Цосле вычисления по этим значениям коэффициентов Фурье-Хаара для первого интервала в момент временн значения чисел в регистрах 5-12 не сбрасываются, а иродолжается процесс перезаписи чисел из предыдущего регистра в последуюн1ий. начиная с регистра 5. Стирается число S в регистре 12, все числа сдвигаются но очереди в стартннй регистр, а в регнстр 5 занисывается число 5, соответствующее второму интервалу. Онределяются коэффцциеиты Фурье-Хаара в момент , (), (см. фиг. 2.6). На следупющем щаге v 2 снова происходит нерезапись чисел из регистра в регистр. Оиределяются коэффициенты Фурье-Хаара иа втором иитервале и т. д. На восьмом шаге v 8 (см. фиг. 2,г) во всех регистрах 5-12 записываются значения интегралов только второго интервала. В момент производится вычисление коэффициентов Фурье-Хаара второго интервала.
7 Предмет изобретения
Устройство для формирования коэффициентов разложения Хаара, содержащее преобразователь аналог-цифра ц блок управления, отличающееся тем, что, с целью повыщения быстродействия, в него введеиы цифровой интегратор, выход которого подключен к последовательно соединенным регистрам сдвига, первая грунна сумматоров, входы которых соединены с выходами соответствующих регистров, первая группа ключей, входы которых соединены с выходами одних сумматоров этой группы, вторая группа сумматоров, входы которых соединены с выходами первой
группы ключей, вторая группа ключей, входы которых соединены с выходами одних сумматоров второй группы, третья группа сумматоров, входы которых соединены с выходами второй группы ключей, а выходы - с соответствующими входами третьей группы ключей, другие входы которых соединены с соответствующими выходами других сумматоров первой и второй групп, вторые входы ключей этой группы подсоединены к одному из выходов блока унравления, другие выходы которого соединены со входом первого регистра и с соответствующими входами ключей первой и второй группы.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения спектральных коэффициентов разложения случайного процесса по функциям Хаара | 1980 |
|
SU935814A1 |
| Устройство для приема информации | 1980 |
|
SU888171A1 |
| Процессор для преобразования цифровых сигналов по Хааро-подобным базисам | 1984 |
|
SU1168966A1 |
| Анализатор спектра хаара | 1978 |
|
SU742952A1 |
| Способ измерения тригонометрических коэффициентов фурье | 1973 |
|
SU473117A1 |
| Анализатор спектра по функциям хаара | 1976 |
|
SU588544A1 |
| Процессор для преобразования цифровых сигналов по Хааро-подобным базисам | 1987 |
|
SU1418745A1 |
| Генератор функций хаара | 1979 |
|
SU783778A1 |
| Генератор функций Хаара | 1980 |
|
SU947847A2 |
| Сейсмостанция | 1987 |
|
SU1430924A1 |

4 2
r
-}
m-1
m-3
J2 2
Авторы
Даты
1975-09-15—Публикация
1974-02-20—Подача