При обработке данных трещинного анализа обычно применяются статистические методы. Результаты замера трещин изображаются графически в какой-либо проекции. При этом, как правило, изображают нормали к плоскостям трещин в виде точек на проекции полусферы. Все дальнейшие статистические операции проводятся над этими точками.
Существующий метод позволяет определять густоту распределения проекций нормалей трещин на полусфере и проводить изолинии густоты их распределения. Для этого проектируют нормали трещин на эквивалентную азимутальную проекцию, затем в полоске бумаги вырезают кружок, площадь которого равна 10%, 1%, 2% или другому какому-либо значению площади полусферы. Кружок этот совмещает с узловыми точками миллиметровой сети, которая предварительно наносится на проекцию. Затем подсчитывают количество точек, находящихся в кружке, число их выражают в процентах от общего числа замеров и относят к центру кружка. Через меченые таким образом точки проводят изолинии процентного распределения замеров.
При всей простоте и наглядности этот метод имеет некоторые недостатки, так как сетка строится в эквивалентной проекции, что необходимо для подсчета густоты точек.
Действительно, только в эквивалентной проекции кружок всегда будет покрывать равные площади, независимо от того, в какой части сетки производится подсчет. Но, как известно, эквивалентная проекция не может быть конформной, вследствие чего и сетка, как всякая эквивалентная проекция, сильно искажает углы, особенно в своей периферической части. Следовательно, кругом будет изображаться на проекции не малый круг полусферы, а какая-то другая фигура, центр которой не совпадает с центром круга (фиг. 1).
Поэтому при отнесении числа, выражающего густоту точек, к центру круга, в котором сделан подсчет, вносится некоторая ошибка в распределении изолиний.
Вторым недостатком известной сетки является общее искажение формы изолиний, также связанной с неконформностью проекции. Это свойство ее мешает определять на глаз характер изолиний и их интерпретировать.
Третьим недостатком сетки является уменьшение масштаба на периферии сетки.
Замеры трещин в поле делаются не с абсолютной точностью. Вследствие неточности инструмента (горного компаса), шероховатости замеряемой поверхности и субъективных качеств геолога в замеры вносится некоторая ошибка. Допустим, что эта ошибка одинакова при измерении простирания и падения трещины. Пусть она равна Δх и выражена в градусах. Практически измерения производят обычно с точностью до 5°, так что можно принять Δх=5°. Для трещинного анализа в основном имеет значение простирание трещин, поэтому сначала выявляется ошибка при определении простирания в зависимости от падения трещины при постоянной ошибке измерения.
Плоскость трещины проектируют в виде ее нормали. Таким образом на сфере плоскость изображается в виде точки (фиг. 2), являющейся проекцией ее нормали. При отклонении плоскости от ее истинного положения во всевозможных направлениях на величину возможной ошибки Δх нормаль ее опишет конус, который спроектируется на сфере в виде малого круга с дуговым радиусом, равным Δх, и центром в точке N выхода нормали истинной плоскости. Проекция нормали к плоскости, определенной измерениями простирания и падения с возможной ошибкой, меньшей или равной Δх, расположится в любой точке внутри или на периферии данного малого круга.
Наибольшая возможная ошибка по азимуту определится углом ΔА между вертикалом ZNB, проходящим через центр N круга погрешности, и вертикалом ZDC, касательным к последнему в точке D. Большой круг HNDR проводится через центр круга погрешности и точку касания его с вертикалом. Сферический треугольник ZND будет прямоугольным, так как дуга ZD является касательной к кругу, a ND радиусом, проходящим через точку касания. Гипотенузой треугольника ZND явится дуга вертикала ZN, равная падению трещины δ. Искомый угол ΔА определится из сферического треугольника соотношением:
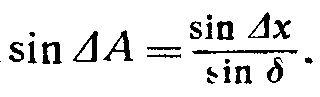
Ошибка при определении азимута простирания трещины изменяется в зависимости от падения последней. При вертикальных трещинах δ=90°. sinδ=1, откуда
sin ΔА=sin Δx и ΔА=Δх,
т.е. ошибка при определении азимута простирания зависит лишь от точности измерения.
При более пологих падениях, когда Δх<δ<90°, sin ΔА>sin Δх ΔА>Δх и тем больше, чем меньше падение трещины.
При δ=Δх, sin ΔА=1 и ΔА=90° ошибка достигает значения четверти окружности в обе стороны от истинного азимута.
В очень пологих трещинах, когда δ<Δх, по данным измерения нельзя судить об истинном азимуте, так как ошибка столь велика, что может дать любое значение простирания. Действительно, в этом случае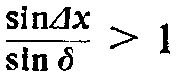 
; зенит располагается внутри круга погрешностей, так что касательного к нему вертикала провести невозможно.
Вышеизложенное объясняет третий из перечисленных недостатков известной сетки. Она имеет наименьший частный масштаб на периферии, куда проектируются как раз наиболее важные и точнее всего измеряемые крутые трещины, а наибольший масштаб - в центре, где располагаются проекции пологих трещин, определенных очень неточно.
Поэтому для изображения трещин рациональнее брать сетку с изменением масштабов, т.е. с более крупным масштабом на периферии, нем в центре. Уменьшение масштаба в центре без ущерба для точности работы может быть даже столь значительным, чтобы находящийся там круг погрешностей сливался в точку.
Нет надобности разрабатывать специальную проекцию со столь ухудшенными качествами в центре. Удобнее для обработки замеров трещин пользоваться стереографической проекцией, преимуществами которой для данного случая являются конформность и увеличение масштаба на периферии.
Ее единственный недостаток - неэквивалентность, но, как известно, эквивалентность несовместима с конформностью проекции, и поэтому с этим недостатком приходится мириться.
Для статистического подсчета на стереографической сетке придется только пользоваться не одним, а несколькими кружками для различных значений падения трещин.
Предметом настоящего изобретения является трафарет для статистической обработки шаровых диаграмм, выполненных в стереографической проекции, в которой для учета изменения масштаба диаграммы от ее центра к периферии трафарет выполнен в виде круга, равновеликого кругу диаграммы с окнами, радиус которых увеличивается от центра к периферии и пропорционален частному масштабу площади зоны диаграммы.
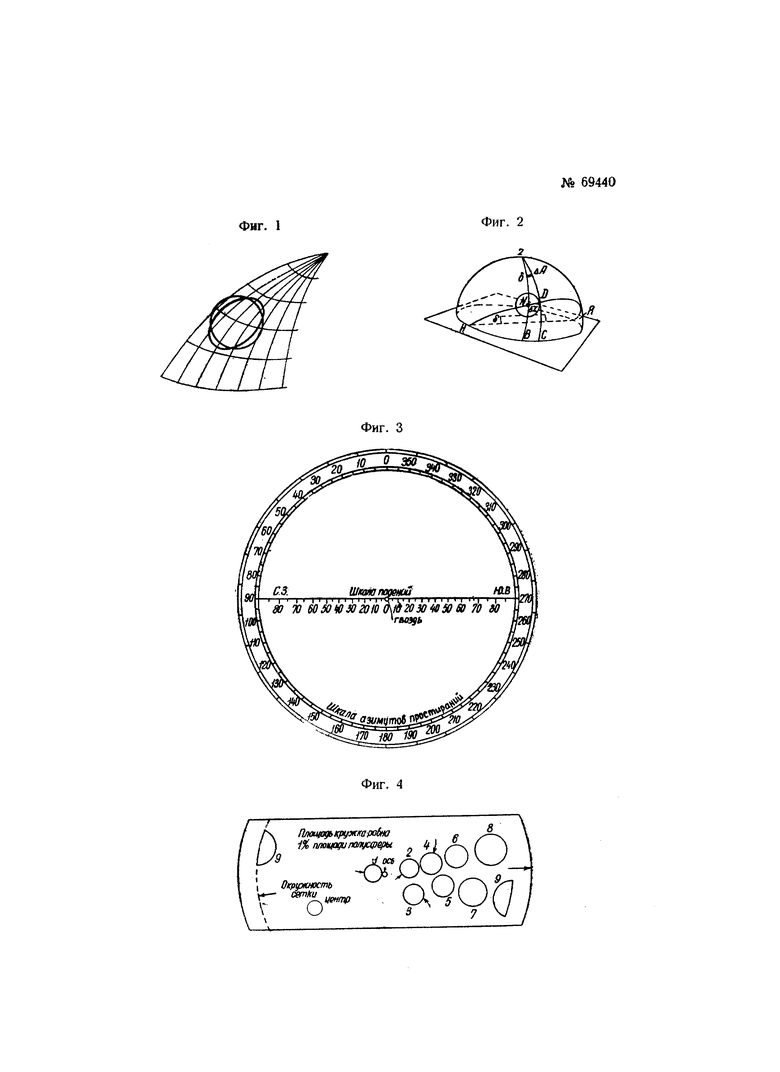
Пользуясь стереографической проекцией, полезно механизировать нанесение на нее точек, как это часто делается и с известной сеткой. Для этого надо начертить на листе плотной бумаги круг с диаметром, равным диаметру сетки (фиг. 3). Круг этот делится через 5° (практическая точность замеров). От верхней точки окружности, считаемой севером, деления надписываются против часовой стрелки. На диаметр, перпендикулярный к направлению С-Ю, наносится стереографическая шкала с нулем в центре круга и 90° - на окружности. Эту шкалу можно снять со стереографической сетки или вычислить по формуле:
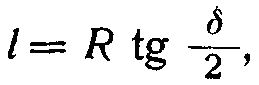
где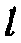 
- расстояние штриха, соответствующего падению от центра сетки, a R - радиус сетки. У восточного конца диаметра делается пометка СЗ, а у западного - ЮВ. Такое расположение пометок делается при проектировании нормали на нижнюю полусферу. При желании проектировать нормаль на верхнюю полусферу, как это обычно делают минералоги и кристаллографы, пометки надо поменять местами.
Вырезанный круг наклеивается на фанеру. Обратную сторону фанеры желательно также оклеить бумагой, чтобы она не коробилась при изменении влажности чертежа. В центр круга втыкается небольшой гвоздь с широкой шляпкой так чтобы острие его выдавалось над плоскостью чертежа на 3-4 мм. Точки наносятся на восковку, накалываемую на гвоздь, который служит ей осью вращения. Для того чтобы восковка не продиралась, в центр ее наклеивается кусочек плотной бумаги или листок целлулоида площадью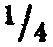 
см2.
Перед накалыванием восковки на ней вычерчивается круг тем же радиусом, что и на фанере. Против точки Севера на этом круге проводится риска - указатель. Для нанесения точки восковка вращается вокруг гвоздя до совмещения риски на ней с азимутом заданного простирания на круге. Теперь остается лишь нанести точку на одном из диаметров по заданному падению. Для статистического подсчета необходимо сделать трафареты кружков заданной площади. Если площадь полусферы равна 2π R2, где R - радиус полусферы, равный радиусу сетки, то площадь кружка в 1% площади полусферы равна:
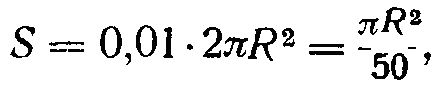
а радиус его
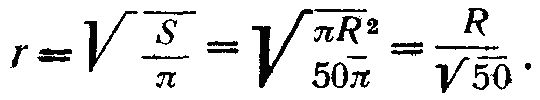
Дуговой радиус кружка определится подстановкой вместо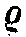 
его значения
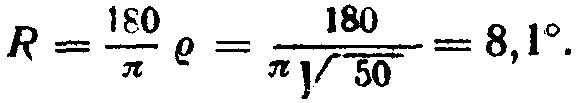
При необходимости подсчета на площади, равной n% от площади полусферы, радиус кружка должен быть увеличен в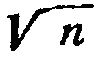 
раз.
Таким образом для кружков различных площадей должны быть взяты следующие дуговые радиусы:
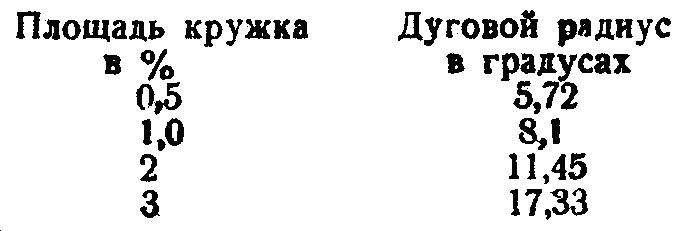
Практически однопроцентные кружки достаточно перекрывают друг друга, если их располагать через 10° по падению.
Для вычерчивания такого кружка берется полоска бумаги шириной приблизительно равной радиусу сетки и длиной несколько больше ее диаметра (фиг. 4). В середине помечается центр сетки, от которого проводится ряд радиусов. По этим радиусам расположатся центры однопроцентных кружков для различных падений. Для каждого значения падения δ размеры кружков могут быть сняты со стереографической сетки или вычислены. В первом случае от значения δ, взятого на экваторе сетки, в обе стороны по экватору откладываются в угловой мере заданные значения углового радиуса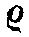 
Середина расстояния между ними принимается за центр кружка, который и проводится циркулем через найденные на экваторе точки. При вычислении расстояния от центра до точек окружности будут равны:
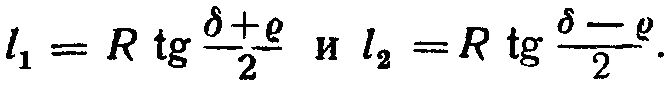
Центр круга расположится посредине между этими точками на расстоянии от центра проекции
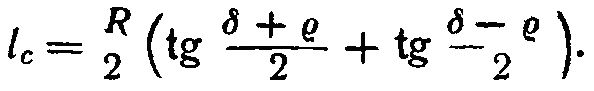
Линейный радиус кружка будет равен половине расстояния между этими точками
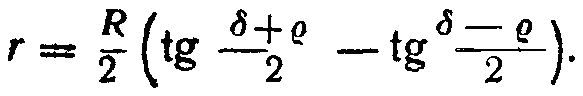
Для значения δ=90° центр кружка будет немного выходить за сетку, и на последней расположится лишь половина круга. Вторая половина его должна быть вычерчена на продолжении диаметра по другую сторону сетки.
Для подсчета бумажку накалывают центром на гвоздик, выступающий в центре фанеры поверх восковки, и поворачивают на постоянную величину. Это значительно легче и делается быстрее, чем совмещение кружка с узлами миллиметровой сетки. При расположении кружков через 10° по падению достаточное перекрытие на периферии получается при повороте трафарета с кружками на 12°; начиная с падения 40°, поворот шаблона можно делать через 24°, для падения в 20° - через 36° и для 10° - через 72°.
Для подсчета горизонтальных трещин в трафарете сделан отдельный кружок, который накладывается на сетку и центрируется с осью от руки.
Для того чтобы облегчить повороты трафарета, на основном круге могут быть нанесены деления через 12°, с которыми поочередно совмещается риска трафарета (фиг. 3). Для кругов, соответствующих 30° и 40°, риска совмещается через одно деление, для 20° - через два на третье и для 10° - через пятое на шестое.
Трафарет для статистической обработки шаровых диаграмм, выполненных в стереографической проекции, снабженный рядом окон с площадью сечения, равной известной кратной части площади полусферы, отличающийся тем, что с целью учета изменения масштаба диаграммы от ее центра к периферии трафарет выполнен в виде круга, равновеликого кругу диаграммы, с окнами, радиус которых увеличивается от центра к периферии и пропорционален частному масштабу площади зоны.
