(54) ГЕНЕРАТОР ДИСКРЕТНЫХ БАЗИСНЫХ ФУНКЦИЙ

| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой функциональный генератор | 1989 |
|
SU1686427A1 |
| Генератор функций Уолша | 1981 |
|
SU964615A1 |
| Анализатор спектра | 1977 |
|
SU789868A1 |
| Устройство для преобразования по функциям Уолша | 1983 |
|
SU1137479A1 |
| Генератор дискретных базисных функций Аристова | 1989 |
|
SU1793435A1 |
| Генератор функций уолша | 1978 |
|
SU742912A1 |
| ГЕНЕРАТОР ДИСКРЕТНЫХ ЭКСПОНЕНЦИАЛЬНЫХ ФУНКЦИЙ | 2008 |
|
RU2371754C1 |
| Генератор функций уолша | 1982 |
|
SU1016777A1 |
| Генератор функций Уолша | 1985 |
|
SU1262470A1 |
| Функциональный преобразователь частота - код | 1984 |
|
SU1228286A1 |


Изобретение относится к автоматике и вычислительной технике и может бБ1ть использовано в системах переда.чи и обработки информации, при построении цифровых фильтров и функциональных преобразователей, в системах управления, а также для анализаторов и синтезаторов сигналов. ,
Известные генераторы дискретных базисных функций предназначены для генерирования функций тригонометрического базиса, базисов Уолша и Хаара 13.
Наиболее близким техническим решением к предлагаемому является известный генератор функций Уолша, содержащий генератор тактовых импульсов, счетчик сумматора по модулю два и многовходовой сумматор по модулю два, причем пары соседних разрядов счетчика соединены со входами сумматоров по модулю два, а выходы сумматоров через элементы .И подключены ко входам многовходового сумматора по модулю два, выход которого является выходом устройства 2.
Недостатком генераторов являются . сравнительно узкие функциональнее З ебйМЬжнбстй, что вызвано как бедным
набором значений периодов генерируемых функций, так и недостаточным для Многих применений спектром значений базисных функций.
Цель изобретения - расширение функциональных возможностей генератора дискретных базисных, функций, состоящее в увеличении числа дискретных базисных значений, принимаемых функ10циями и их периодом.
Поставленная цель достигается тем, что известный генератор дискретных базисных функций, содержащий генератор тактовых импульсов содержит п - 1
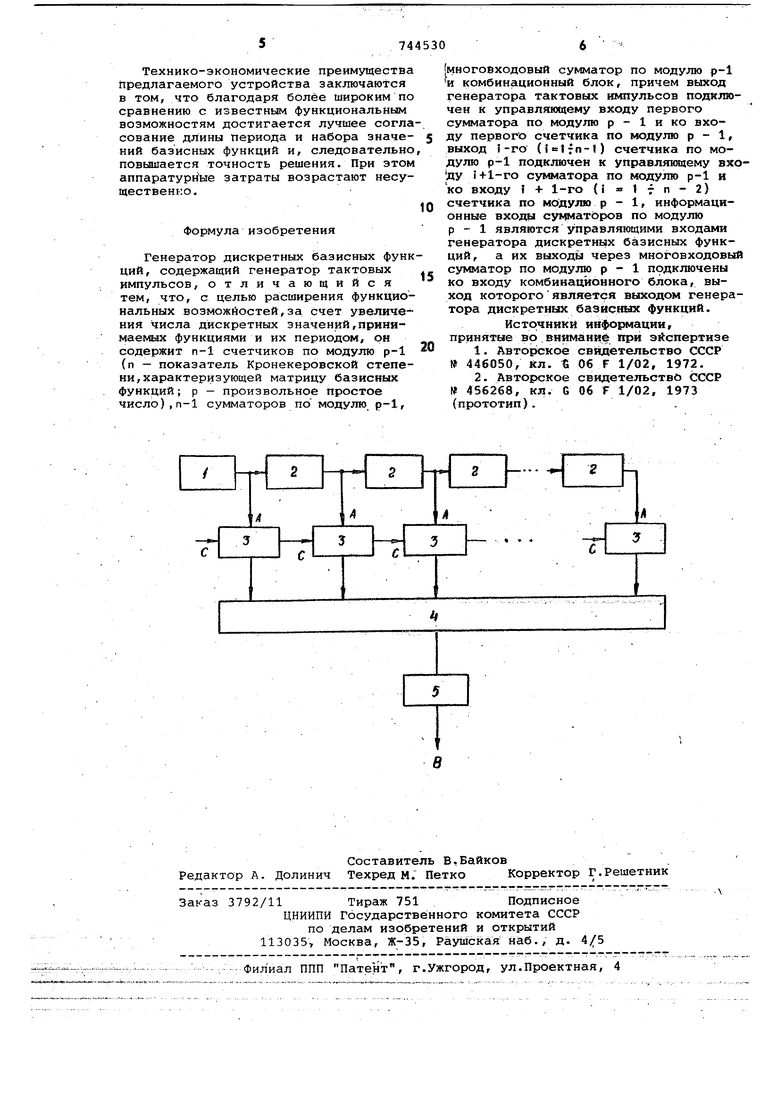
15 счетчиков по модулю р - 1 (п - показа тель Крояекеровской степени, характеризукяцей матрицу базисных функйий, р - произвольное простое число), п-1 сумматоров по модулю р - 1, многовхо20довой сумматор по модулю р - 1 и комбинационный блок, причем выход генератора тактовых импульсов подключен к управляшадему входу первого сумматора по модулю р - 1 и ко входу пер25вого счетчика по модулю р - 1, выход i-ro (i 1 7 n 1) счетчика по модулю р - 1 подключен к управляющему входу i + 1-го сумматора по модулю р-1 и ко входу i 1-го (i« l-:n-2)
30 счетчика по модулю р-1, информацио ные входы сумматоров по модулю рявляются управляющими входами гене тора дискретных базисных функций, а их выходы через многовходовой су матор по модулю р - 1 подключены к йходу комбинационного блока, выход которого является выходом генерат ра, лнскретных базисных функций. На чертеже представлена функцио нальная схема генератора дискретных базисных функций. Он содержит генератор 1 тактовы импульсов, п - 1 счетчиков 2 по мо дулю р - 1I п - 1 сумматоров 3 по модулюр - 1, многовходовый сумматор 4 по модулю р - 1, комбинационный блок 5. Такой генератор позволяет генерировать базисные функции, принима щие (р-1) целых значений (р - пр извольное простое число), например наименьших абсолютных вычетов по p-l И,...гМ,модулюz , г Кроме того, обеспечивается весьма шй:рокий набор периодов базисных функций N (р -1), где п - любо натуральное, MeJiaMtfsfM пострбения базисных фу ций можно пояснить следующим образ Для произвольного простого р выбирается преобразованный корень g и строится матрица Gp (..p) где I, j - номер строки и столбца . . соответственно. Например, исходн ае матрицы при р ()ир 7 () имеют вид П 1 1 1 1 2-1-21 1-1 1-lj U-2-1-2/ fl 1 1 1 1 1 1 3 2-1-3-2 1 2-3 1 2-3 1-1 1-1 1-1 1-3 2 1-3 2 1-2-3-1 2 3/ В частности, при р 3 (g -1) мо но получить исходную матрицу Уолша /1 1 41 -il Для получения нужного периода бази ных функций следует образовать мат рицу , где п - символ возвед ния матрицы в -ую Кронекеровскую степень. Использ гя свойства суммы степеней элементов мультипликативн группы конечного поля, можно доказать, что матрицы G образуют ба зис в конечномерном векторном пространстве над полем характеристики 4 обратную матрицу Г р можно построить следующим образом .-i.(i-i){j-ii cH:i.,tni -((} ),Гр «р Gr, Ь 1 1(mod р), Н - единичная Строки построенных матриц матрица (и,пи Гр ) и образуют искомые р базисные функции. Устройство работает следующим образом,. Накапливающие сумматоры 3 в начальном состоянии сброшены в нуль; на их информационные входы подаются коды уменьшенного на единицу номера генерируемой строки матрицы 6р. Таким образом на выходе сумматоров образуется последовательность индексов по модулю р. Команды на сумгчирозание (накопление) индексов вырабатывается с помощью цепочки счетчиков 2, чей и обеспечивается возведение исходной матрицы в Кронекеровскую степень. Коды с выходов сумматоров 3 суммируются многовходовым cyivaiaTOpoM 4, на выходе которого образуется суммарный индекс, равный индексу произведения . /jii odp-l), где ij - индекс j-ro сомножителя по модулю р при первообразном д . Таким образом, трудоемкая операция возаеденяя в степень (умножения) заменена на простую операцию сложейия инлексов. Суммарный индекс поступает на комбинационнь1й блок 5, на выходе В которого и образуется искомая последовательность наименьших неотрйдательных вычетов, т.е. одна из базисных функций. Комбинационный блок 5, таким образом, осуществляет преобразование индексов в вычеты И может быть синтезирован любыми известными методами по таблице индексов . При необходимости генерирования полного набора базисных функций блок управ/гения последовательно изменяет коды на информационных входах С сумматоров 3. В качестве примера ниже приведена матрица базисных функций для случая р 5, 9 2, п 2. 1 1 11 /1111 11111111 1 2-1-2 1 2-1-2 1 2-1-2 1 2-1-2 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-2-1 2 1-2-1 2 1-2-1 2 1-2-1 2 2222 -1-1-1-1 -2-2-2-2 1111 -1-2 12-21 2-1 2-1-2 1 1 2-1-2 1-1 1-1 2-2 2-2 -1 1-1 1 -2 2-2 2 2 1-2-1 -1 2 1-2 -2-1 2 1 1-2-1 2 -1-1-1-1 1111 -1-1-1-1 1111 1 2-1-2 -1-2 121 2-1-2 -1-2 1 2 1-1 1-1 -1 1-1 1 1-1 1-1 -1 1-1 1 1-2-1 2 -1 2 1-2 1-2-1 2-12 1-2 1111 -2-2-2-2 -1-1-1-1 2222 1 2-1-2 -2 1 2-1 -1-2 1 2 2-1-2 1 1-1 1-1 -2 2-2 2 -1 1-1 1 2-2 2-2 1-2-1 2 -2-1 21-12 1-2 2 l-2-ll Технико-экономические преимущества предлагаемого устройства заключаются в том, что благодаря более широким по сравнению с известным функциональным возможностям достигается лучшее согла сование длины периода и набора значеНИИ базисных функций и, следовательно повьииается точность решения. При этом аппаратурные затраты возрастают несущественно. Формула изобретения Генератор дискретных базисных функ ций, содержащий генератор тактовых импульсов, отличающийся тем, что, с целью расширения функциональных возможйостей,за счет увеличения числа дискретных значений,принимаемых функциями и их периодом, он содержит п-1 счетчиков по модулю р-1 (п - показатель Кронекеровской степени, характеризующей матрицу базисных функций; р - произвольное простое число),п-1 сумматоров помодулю р-1. многойходовый сумматор по модулю р-1 и комбинационный блок, причем выход генератора тактовых импульсов подключен к управляющему входу первого сумматора по модулю р - 1 и ко входу первого счетчика по модулю р - 1, выход 1-го (letfn-l) счетчика по модулю р-1 подключен к управляющему вхо;ду i+1-го сумматора по модулю р-1 и ко входу { + 1-го {i I 7 п - 2) счетчика по модулю р - 1, информационные входы сунматЬров по модулю р-1 являются Управляющими входами генератора дискретных базисных функций, а их выходы через многовходовый сумматор по модулю р-1 прдключены ко входу комбинационного блока, выход которогоявляется выходом генератора дискретных базйс шх функций. Источники информации, принятые во виимани при эйспертизе 1.Авторское свидетельство СССР 446050, кл. е Об F 1/02, 1972. 2.Авторское свидетельство СССР № 456268, кл. G Об F 1/02, 1973 (прототип).
Авторы
Даты
1980-06-30—Публикация
1978-03-24—Подача