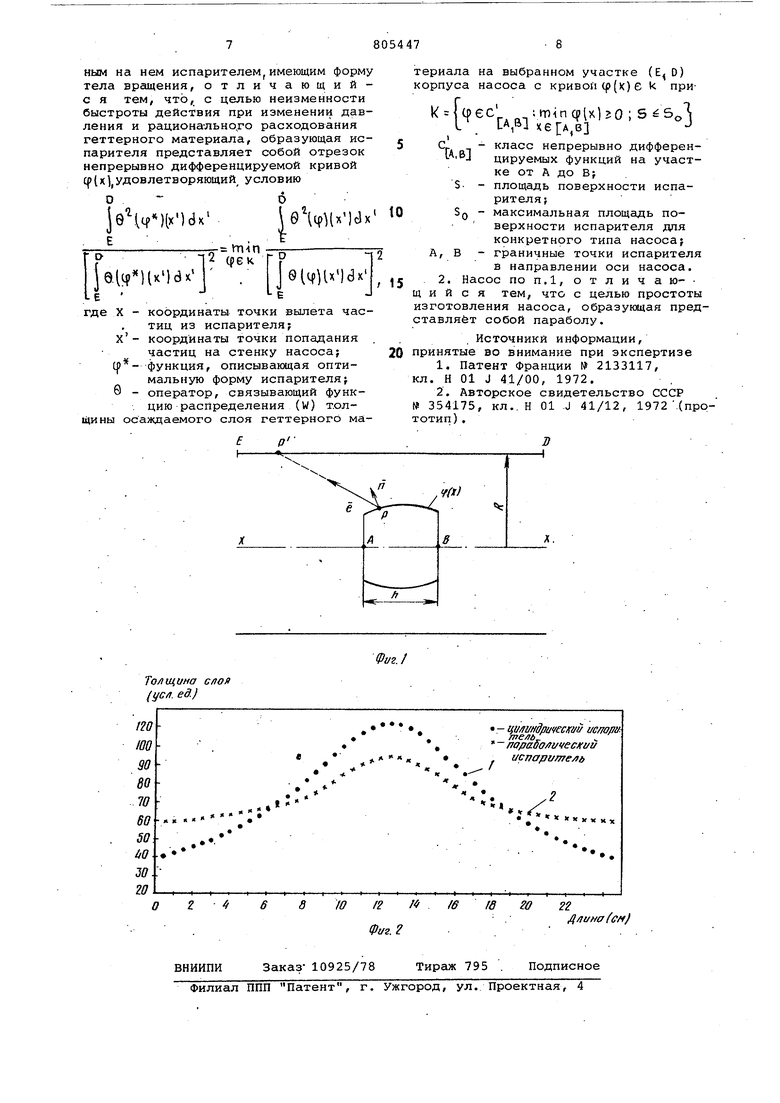
(54) ГЕТТЕРНО-ИОННЫЙ НАСОС ОРБИТРОННОГО ТИПА пыления геттера быстрота действия на соса будет увеличираться до какогото постоянного- значения, но при этом геттерный материал в центральной час ти образующейся пленки будет использоваться неэффективно, поскольку нанесенный слой геттера, не успев на .себе связать молекулы откачиваемого газа, будет запылен новым слоем геттера. В области высоких давлений уменьшения быстроты действия насоса компенсируют увеличением скорости испарения геттера, а от неэффективности использования геттера в центральной части пленки в некоторых слу чаях избавляются тем, что устанавливают над запыленной поверхностью нес колько точечных источников j . Такое решение вопроса имеет свои недос татки. Например, изменение мощности подводимой-к испарителю в зависимоети от давления требует введение какой-либо следящей системы, а при использовании нескольких испарителей может нарушаться принцип работы орби ронного насоса т.е. тот принцип, за счет которого этот тип насоса откачи вает инертные газы (при использовании нескольких испарителей длина про бега электронов падает, тем самым уменьшается вероятность ионизации и скорость ионной откачки). Известен также геттерно-ионный насос орбитронного типа, содержащий цили1здрический корпус, стержневой .анод с расположенным на нем испарителем, имеющим форму тела вращения .Недостаток известного устройства заключается в том, что при нанесении из цил-индрической втулки-испарителя на внутреннюю поверхность корпуса насоса геттерной пленки, образующийся слой геттерного материала неоднороден по толщине. Таким образом, если рассмотреть толщину образующейся пленки по. оси насоса, то можно видеть, что наибольшее запыление образуется на корпусе насоса в области -непосредственной близости от втулкииспарителя на длине равной 2+3 длина втулки. На отдаленных периферийных участках степень запыления уменьшает ся. В существующих конструкциях орбитронных насосов соотношение длины втулки испарителя к длине корпуса насоса обычно выбирается равным -1/15+1/20, т.е. можно видеть, какая малая часть поверхности корпуса подвергается равномерному запылению. Цель изобретения - неизменность быстроты действия при изменении давления и рациональное расходование геттерного материала. Поставленная цель достиг-ается тем что .образующая испарителя представляет собой отрезок непрерывно дифференцируемой кривойср х) удоылетворяющей условию D )dx Г г J0itp iuia j где X координаты точки вылета частиц из испарителя; координаты точки попадания частиц на стенку насоса; функция, описывающая оптимальную форму испарителя оператор, связывающий функцию распределения (W)толщины - осаждаемого слоя геттерного материала на выбранном участке (E,D). корпуса насоса с кривой ((.} е при Ч f А -, о 1 L LA.BJ хеГА.в . J класс непрерывно дифференцируемых функций на участке от А до В} площадь поверхности испарителя ; максимальная площадь поверхности испарителя для конкретного типа насоса , граничные точки испарителя в направлении оси насоса. С целью простоты изготовления насоса образующая испарителя представляет собой параболу. На фиг. 1 представлена система состоящая из двух поверхностей: цилиндрической радиуса .Р и соосной с ней поверхности вращения, получаемой от вращения отрезка непрерывной дифференцируемой кривойф(х) вокруг общей оси , на фиг. 2 - результаты рассчета оптимальной формы испарителя для насоса внутренним диаметром мм и площадью испарителя ,7 см . Указанные (фиг. 1) поверхности являются моделями внутренней поверхности насоса и втулки-испарителя соответственно. Из каждой точки Р испарителя в направлении f испускаются молекулы с интенсивностью ,,1 , где Зд- полная интенсивность, нормали к поверхности вращения в точке Р ,С -орт в направлении выхода частиц из точки Р. nycTbW(x)- функция распределения толщины осаждаемого слоя геттерного материала за единицу времени по длине насоса. Х их отсчитываются по . оси цилиндра от некоторой фиксированной точки А, лежащей на торце испарителя. Необходимо найти оператор 0 такой, (ф)|И определить оптимальную (например, в смысле метода наименьших квадратов)форму втулки из условия (1) ОD )1кМбх 2( jti / 1 1 I л2/ ,- I .,1 e() Е о-|2 D je txld; eitp K lcix где Е, Д - участок цилиндрической поверхности на которой требуется равномерность напыляемого слоя-, ( функция, описывающая оптимальную форму испарите координаты точки попадания частиц. ГТ ;тчпс()(х), V-
.j,,.|-f Г . 4 fUUx.-x)4Rco5t -Ci(.0
iyU-))-2Rq.(xlco5r2.V2
rj агс cos
тал
teio.i) t - параметр, характеризующий попадание частиц на стенку насо са, и изменяющийся от О до 1; h.- длина испарителя. Ввиду того, что подынтегральная функция не интегрируема в явном виде нахождение конкретного распределения W(x) при заданной ф (х) проводится методами численного интегрирования. В результате находится значение W(x) в узлах некоторой наперед заданной сетки на оси х . Выбор оптимальной функции() производится после того, как были построены графики W(x) для нескольких конкретных геометрий испарителя. Исходя из технологических возможнос тей изготовления испарителя в производ ве на металлорежущих станках, допустимым является выбор формы испарителя , описываемой многочленом порядке не более двух. В связи с этим ограни чением оптимальная форма испарителя искалась среди кривых (f(x) принадлежащих классу парабол K |cj ек; Ц)(х Ох - Ъхц-сЯ « По изложенному алгоритму была сос тавлена программа на языке ФОРТРАН для ЭВМ ЕС-1022. В качестве, исходных величин в Мсшшну вводятся: -радиус цилиндрической поверхности насоса J ; -длина испарителя h;
2)
q,x4tU- 0-4)()(
2te()()R 7 S - площадь поверхности iu;;...; . теля; А,В - граничные точки испарители в направпении оси насоса) Sp- максимальная .площадь поверхности испарителя для конкретного типа насоса , - класс непрерывно дифференцируемых функций на участке от А до В. Для решения задачи зафиксируем какую-нибудь производную точку Р на поверхности цилиндра (с координатой х ) и найдем количество геттерного материала, поступающего сюда за единицу времени со всей поверхности испарителя. Искомая величина получается интегрированием интенсивности j по криволинейной поверхности испарителя, видимой из данной точки р . Таким образом мы находим инт-ересую нас оператор, связывающий W и Ц) дай следующем виде В CJ -- коэфф.ициент параболы а, в, с; .-общее количество узлов на осях X и х и угловой равномерности 1 Вычисление интеграла (2) производится по методу Симпсона. Кривая 1 (фиг.. 2) соответствует распределению ( толщины Напыляемого слоя гетте)Ц(лч; материала с цилиндрической втулки-испарителя диаметром 8 мм и длиной 15 мм. Кривая 2 соответствует растределению толщины напыляемого слои п испарителя, имеющего параболическую форму поверхности. Поверхность получена вращением параболы с коэффициентами ,07; Ъ 1,05-, ,. Площадь поверхности цилиндрического и параболического испарителя равны. Как видно из чертежа равномерность напыленного слоя параболического испарителя выше. Данная форма испарителя является, в смысле метода наименьших квадратов, для данной конструкции орбитронного насоса оптимальной . Предложенная конструкция испарителя позволит в геттерно-ионных насосах улучшить технические характеристики насоса и рационально использовать геттерный материал. Формула изобретения 1. Геттерно-ионный насос орбитронного типа, содержащий цилиндрический корпус, стержневой анод с расположенным на нем испарителем,имеющим форму тела вращения, отличаю щийс я тем, что, с целью неизменности быстроты действия при изменении давления и рациона-льно го расходования геттерного материала, образующая испарителя представляет собой отрезок непрерывно дифференцируемой кривой СР(х удовлетворяющий условию
О О
)dK Ui4 HlcJx
F . fc
- m-in I (рек
eitflUM
9.it Ux4dx
где X - координаты точки вылета частиц из испарителя; Х- координаты точки попадания .
частиц на стенку насоса; функция, описывающая оптимальную форму испарителя} Q - оператор, связывающий функ. цию распределения (W) толщины осаждаемого слоя геттерногО материала на выбранном участке () корпуса насоса с кривой ф(х)е k приЬ ГАЛТ 1 0 -М
К
L LA,BJ 1(6 А,в
D
класс непрерывно дифферен:д,в цируемых функций на участке от А до В;
s. площадь поверхности испарителя
5л максимальная площадь поверхности испарителя для конкретного типа насоса
A, В граничные точки испарителя в направлении оси насоса. 2. Насос ПОП.1, отличаю-щ и и с я тем, что с целью простоты изготовления насоса, образующая представляет собой параболу.
Источники информации, принятые во внимание при экспертизе
1.Патент Франции № 2133117, кл. Н 01 J 41/00, 1972.
2.Авторское свидетельство СССР
№ 354175, кл.. Н 01 J 41/12, 1972.(пртотип) .
У


| название | год | авторы | номер документа |
|---|---|---|---|
| Ионно-геттерный насос | 1983 |
|
SU1102408A1 |
| Способ управления скоростью распыления материала в геттерном насосе и устройство геттерного насоса | 2017 |
|
RU2661493C1 |
| Способ откачки газов и электродуговой испарительный насос | 1983 |
|
SU1152433A1 |
| Магниторазрядный насос и способ его изготовления | 1979 |
|
SU886097A1 |
| Электродуговой испаритель | 1978 |
|
SU693988A1 |
| НЕРАСПЫЛЯЕМЫЙ ЛЕНТОЧНЫЙ ГАЗОПОГЛОТИТЕЛЬ И СПОСОБ ЕГО ПОЛУЧЕНИЯ | 1994 |
|
RU2073737C1 |
| МАГНИТНЫЙ ЭЛЕКТРОРАЗРЯДНЫЙ НАСОС | 1985 |
|
SU1321310A1 |
| ИНСТРУМЕНТ ДЛЯ ВЫГЛАЖИВАНИЯ | 1991 |
|
RU2014985C1 |
| УСОВЕРШЕНСТВОВАННЫЙ ВЫСОКОМОЩНЫЙ ГЕТТЕРНЫЙ НАСОС | 1993 |
|
RU2082251C1 |
| Сорбционный вакуумный насос | 1987 |
|
SU1520258A1 |


Авторы
Даты
1981-02-15—Публикация
1979-03-20—Подача