УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ ОТ ЧИСЛА Российский патент 1994 года по МПК H03M7/18 G06F7/72 

Изобретение относится к вычислительной технике и может быть использовано в устройствах для формирования элементов конечных полей, в устройствах для формирования кодовых последовательностей, построение которых основывается на теории конечных полей, а также в вычислительных устройствах, функционирующих в СОК.

Цель изобретения - расширение функциональных возможностей за счет определения значения частного.

Сущность изобретения заключается в следующем. Пусть
A = QP + γ. (1)
Задача состоит в том, чтобы по известным А и Р отыскать остаток γ и частные Q. Остаток γ является, говоря терминами теории чисел, вычетом числа А по модулю Р, поэтому
A = γ (mod P) (2)
Значение остатка γ может быть вычислено следующим образом. Число А может быть представлено в позиционной системе счисления в виде
A= a_n-12^n-1+a_n-22^n-2+ . . . +a₁2+a₀, (3) где a_i, i = 0, n-1 - коэффициенты, принимающие значение 0 или 1 в зависимости от значения числа А; n - количество разрядов в представлении числа А. Тогда
γ= A(modP)= (a_n-12^n-1+a_n-22^n-2+ . . . +a₁2+a₀)modP. (4)
Выражение (4) может быть легко представлено в следующем виде:
γ= ((. . . (a_n-12+a_n-2)2+. . . +a₁)2+a_o)modP (5)
Из теории чисел известно, что операция приведения по модулю инвариантна к сложению и умножению, т. е. величина остатка не зависит от того, вычислен он от суммы (произведения) или от каждого слагаемого (сомножителя), а затем соответствующие частичные остатки просуммированы (перемножены) и от результата вычислен остаток по модулю.

Исходя из вышесказанного, выражение (5) может быть представлено в виде
γ= ((. . . (a_n-12+a_n-2)(modP)2+a_n-3)(modP)2+. . . +a₁)(modP)2+a_o)(modP) (6)
В таком виде значительно облегчается задача нахождения остатка γ от числа А, так как вычисление остатка происходит от чисел, не превышающих по своему значению величину 2Р-1. Так как a_i принимает значение 0 или 1, то выражение a_n-2 2 + a_n-2 для любых Р > 2 не превышает величины 2Р-1. В таком случае алгоритм приведения по модулю заключается в следующем. Если величина числа не превышает величины модуля Р, то данное число остается без изменения, если величина числа находится в пределах от Р до 2Р-1, то из него вычитается величина модуля Р и остаток оказывается меньше величины модуля Р. Операция сравнения величины числа, приводимого по модулю, с модулем Р, а также вычитания из числа модуля Р может быть реализована на одном комбинационном сумматоре. Величина модуля Р, подаваемая на один вход сумматора, должна быть представлена в дополнительном двоичном коде (для перевода числа из прямого двоичного кода в дополнительный достаточно проинвертировать все разряды и к полученному числу прибавить единицу), а величина числа, которое необходимо привести по модулю, должна быть представлена в прямом двоичном коде, который подается на второй вход комбинационного сумматора. Если в результате суммирования указанных величин на выходе переноса сумматора появляется единица, то это значит что число, двоичный код которого подается на второй вход сумматора, больше или равно по своему значению величине модуля Р (дополнительный двоичный код которого подан на первый вход сумматора), а если на выходе переноса сумматора появляется ноль, то число меньше модуля. Следовательно, наличие нуля на выходе переноса сумматора говорит о том, что вычитание не требуется, а наличие единицы - о необходимости вычитания из числа величины модуля. Вычитание осуществляется этим же сумматором, т. е. на его выходах образуется двоичный код разности чисел, поданных на его входы.

Таким образом, приведение по модулю Р числа, лежащего в диапазоне от 0 до 2Р-1, осуществляется с помощью одного комбинационного двухвходового сумматора, на один вход которого подается в дополнительном коде величина модуля Р, а на другой вход - в прямом коде код числа. Остаток данного числа по модулю Р формируется на выходе сумматора, если на его выходе переноса единица, или снимается со второго входа, если на выходе переноса сумматора ноль. Операцию выборки осуществляют с помощью мультиплексора, который управляется сигналом с выхода переноса сумматора. Этот сигнал является одним из разрядов частного Q.

Итак, в результате выполнения операции (a_n-1 2 + a_n-2)(mod P) получилось число, по своему значению лежащее в диапазоне от 0 до Р-1 и один (n-2)-й разряд частного Q. Назовем это число (n-2)-м частичным остатком от числа А по модулю Р. Далее согласно выражению (6) осуществляется умножение (n-2)-го частичного остатка на два и прибавление к полученному произведению коэффициента a_n-3. Так как (n-2)-й частичный остаток ≅ Р-1, то величина числа ((a_n-1 2 +a_n-2)(mod 2)2 + a_n-3) лежит в диапазоне от 0 до 2Р-1. Получение (n-3)-го частичного остатка осуществляется вышеописанным методом и т. д. до тех пор, пока не будет получен последний частичный остаток, который и будет остатком γ от числа А по модулю Р. Сигналы с выходом переносов соответствующих сумматоров являются разрядами частного Q. Операция умножения на два во всех случаях осуществляется сдвигом всех разрядов множимого на один в сторону старших. Суммирование осуществляется обычным способом с применением комбинационных двоичных сумматоров.

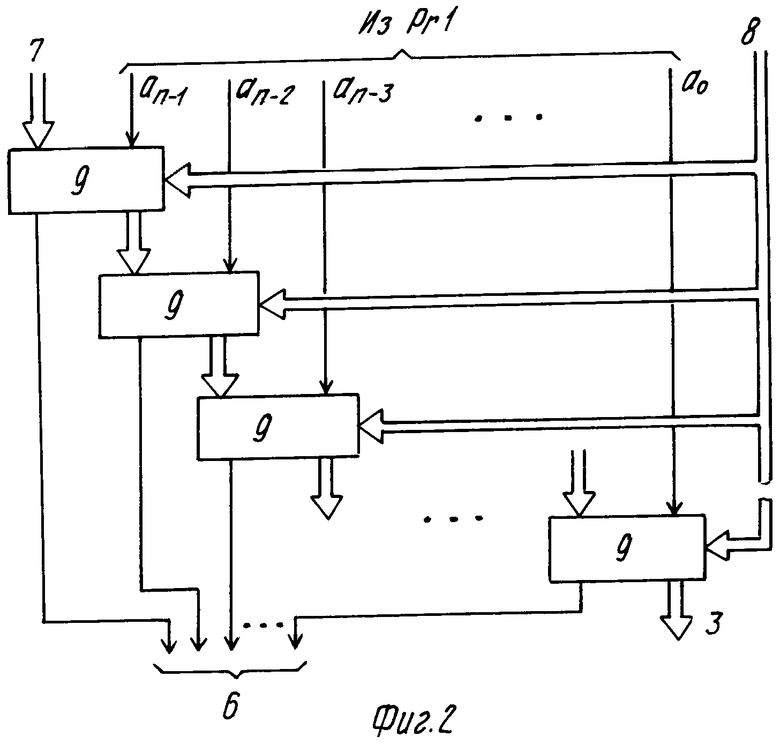
На фиг. 1 представлена функциональная схема устройства; на фиг. 2 - функциональная схема блока формирования частного и остатка; на фиг. 3 - функциональная схема сумматора по модулю.

Устройство содержит (фиг. 1) регистр 1 и блок 2 формирования частного и остатка, выход 3 остатка γ , вход 4 кода числа А, вход 5 "Начало вычисления", выход 6 частного Q, вход 7 переноса, вход 8 инверсного кода модуля Р.

Блок 2 формирования частного и остатка содержит (фиг. 2) n сумматоров 9 по модулю (где n - разрядность регистра 1).

Сумматор 9 по модулю (фиг. 3) содержит первый 10 и второй 11 сумматоры и мультиплексор 12.

Устройство работает следующим образом.

В исходном состоянии (фиг. 1) на вход модуля подается инверсный код модуля P_j, по которому необходимо формировать остатки. Число А_к через вход 4 поступает на информационные входы регистра 1. Одновременно на вход 5 "Начало вычисления" подается импульс, который поступает на вход записи регистра 1, по которому код числа А_к записывается в регистр 1 и передается на управляющие входы блока 2 формирования частного и остатка.

В блоке 2 формирования частного и остатка (фиг. 2) код числа поступает поразрядно на информационные входы первой группы сумматоров 9 по модулю. Первый информационный вход 7 первого сумматора 9 по модулю предназначен для подачи частичного остатка с выхода формирователя остатка такого же устройства при необходимости увеличения разрядности числа А_к. Так как на информационные входы сумматоров 9 информация подается в прямом коде, а инверсный код модуля в каждом из них преобразуется в дополнительный код, то на выходе каждого сумматора 9 по модулю, начиная со старших разрядов числа, сформирован частичный остаток, который на выходе n-го сумматора 9 по модулю и будет остатком γ числа А_к по модулю Р_j. Разряды переноса каждого сумматора 9 по модулю являются разрядами частного.

Сумматор 9 по модулю (фиг. 3) работает следующим образом. Перемноженный на два частичный остаток (путем сдвига разрядов на один в сторону старших) и разряд числа А_к поступают на входы сумматора 10, где суммируются, а затем результат суммирования поступает на первые входы сумматора 11 и первые входы мультиплексора 12. Если значение суммы превышает значение модуля, то в сумматоре 11 за счет перевода инверсного кода модуля в дополнительный код происходит вычитание из полученной суммы значения кода модуля, на выходе переноса сумматора 11 появляется управляющий сигнал, переключающий вторые информационные входы мультиплексора 12 на его выходы, и значение частичного остатка с выходов сумматора 11 через вторые входы мультиплексора 12 поступает на информационные выходы 3. Управляющий сигнал на выходе переноса сумматора 11 одновременно является разрядом частного и поступает на выход 6 устройства.

При следующем цикле формирования частного и остатка задается любое другое число А_l, которое поступает на вход 4, и работа всех элементов и блоков устройства повторяется.

Для смены модуля на вход 7 устройства подается очередной код модуля Р_i, а с подачей очередного числа A_m работа элементов и блоков устройства повторяется.

Изобретение относится к вычислительной технике и может быть использовано в устройствах для формирования элементов конечных полей, в устройствах для формирования кодовых последовательностей, построение которых основывается на теории конечных полей, а также в вычислительных устройствах, функционирующих в СОК. Цель изобретения - расширение функциональных возможностей за счет определения как значения остатка, так и значения частного. Устройство содержит регистр и блок формирования частного и остатка, состоящий из n сумматоров по модулю. 2 з. п. ф-лы, 3 ил.

1. УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ ОТ ЧИСЛА, содержащее регистр, отличающееся тем, что в него введен блок формирования частного и остатка, информационные входы первой группы которого соединены с выходами регистра, информационные входы которого соединены с входами кода числа устройства, а управляющий вход - с входом "Начало вычисления" устройства, информационные входы второй группы блока формирования частотного частного и остатка соединены с входами инверсного кода модуля устройства, информационные входы третьей группы - с входами переноса устройства, выходы частного и остатка которого соединены соответственно с первыми и вторыми выходами блока формирования частного и остатка. 2. Устройство по п. 1, отличающееся тем, что блок формирования частного и остатка содержит n сумматоров по модулю (где n - разрядность регистра), первый вход i-го сумматора по модулю (i = 1, . . . , n) соединен с i-м информационным входом первой группы блока, вторые входы всех сумматоров объединены и соединены с информационными входами второй группы блока, выходы разрядов суммы j-го сумматора по модулю (j = 1, . . . , n - 1) соединены со сдвигом всех разрядов на один в сторону старших с третьим входом (j + 1)-го сумматора по модулю, третий вход первого сумматора по модулю соединен с информационными входами третьей группы блока, выходы разрядов суммы n-го сумматора по модулю соединены с вторыми выходами блока, первые выходы которого соединены с выходами переноса всех сумматоров по модулю. 3. Устройство по п. 2, отличающееся тем, что сумматор по модулю содержит мультиплексор и два сумматора, причем вход первого слагаемого сумматора соединен с первым входом сумматора по модулю, третий вход которого соединен с входом второго слагаемого первого сумматора, выход которого соединен с входом первого слагаемого второго сумматора и первым информационным входом мультиплексора, второй информационный вход которого соединен с выходом суммы второго сумматора, вход второго слагаемого которого соединен с вторым входом сумматора по модулю, вход переноса второго сумматора соединен с шиной логической единицы, выход переноса второго сумматора соединен с управляющим входом мультиплексора и выходом переноса сумматора по модулю, выход разрядов суммы которого соединен с выходом мультиплексора.