ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО Российский патент 1994 года по МПК H03M7/18 

Изобретение относится к вычислительной технике и может быть использовано в устройствах для формирования элементов конечных полей, в устройствах для формирования кодовых последовательностей, построение которых основывается на теории конечных полей, а также в арифметических устройствах, функционирующих в СОК и в арифметических сопроцессорах.

Известно устройство для формирования остатка по произвольному модулю от числа (см. авт.св. СССР N 1520667, кл. H 03 M 7/18, 1988), выбранные в качестве прототипа и содержащее два счетчика, блок определения кратности чисел, группу программируемых логических матриц, элемент И-ИЛИ, дешифратор, регистр, элемент запрета, элемент И, элемент задержки и элемент ИЛИ, соединенные между собой функционально.

Недостатком известного устройства являются его низкие функциональные возможности, так как оно не позволяет определить значение цифр неполного частного.

Цель изобретения - расширение функциональных возможностей за счет вычисления цифр неполного частного.

Сущность изобретения заключается в следующем. Пусть
A = QP + γ , (1) где А - число, от которого необходимо вычислить остаток по модулю Р;
Q - неполное частное, образующееся при делении числа А на модуль Р;
γ - остаток, который необходимо вычислить от числа А по модулю Р, лежащий в интервале от 0 до Р-1.

Неполное частное Q может быть представлено в позиционной системе счисления в виде
Q = q_k-1 m^k-1 + ... + q₁m + q_o, (2) где m - основание системы счисления;
q_i - коэффициенты системы счисления,
i=, q_i=;
k - разрядность числа Q.

Согласно выражению (1) остаток γ может быть вычислен как
γ = A - QP. (3)
Подставляя выражение (2) в уравнение, имеют
γ = A - q_k-1 m^k-1 P - ... - q₁mP - q_oP (4)
Обозначают A_o = A - q_k-1 m^k-1 P, а A_i=A_i-1 - q_k-1-i m^k-1-i,где i = 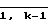, тогда выражение (4) может быть записано в виде
γ = A_o - q_k-1 m^k-1P - ... - q₁mP - q_oP = ... = A_k-2 - q₁mP - q_o = A_k-1 q_oP = A_k . (5)
Из выражения (5) видно, что задача вычисления остатка γ по модулю Р от числа А сводится к отысканию числа A_k. Вначале вычисляется A_o = A - q_k-1 m^k-1 P. Учитывая, что γ- положительное число, А_о не может быть меньше нуля. Это условие обеспечивается соответствующим выбором коэффициента q_k = . Далее последовательно вычисляются числа A_i = A_i-1 - q_k-1 m^k-1 P, i = . Условие A_i ≥ 0 выполняется аналогично соответствующим подбором коэффициента q_k-1. Последнее число A_k и является остатком числа А по модулю Р.

Итак, задача вычисления остатка γ от числа А по модулю Р сводится к последовательному вычитанию из числа А величин q_imⁱP, i = 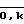, q_i = 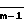. Выбором величины m можно регулировать быстродействие вычисления остатка. Очевидно, что с увеличением m количество последовательных вычитаний в выражении (4) уменьшается. Кроме того, если m является степенью двойки, то вычисление произведения mⁱР является тривиальным и заключается в сдвиге на i разрядов в сторону старших величины числа Р. Умножение на q_i в большинстве практических случаев также тривиально. Количество вычитаний типа A_i-1 - q_k-i m^k-iP, q_k-i= с увеличением m увеличивается. Однако эти вычисления могут быть выполнены параллельно, для чего все же требуется m-1 вычитателей, т.е. увеличение быстродействия нахождения остатка приводит к росту аппаратурных затрат. Проверка условий А < 0 также может быть сведена к тривиальной задаче путем использования выходов переноса вычитателей для управления выбором необходимого коэффициента q_k-i. Примечательно также, что эти же выходы могут служить в качестве выходной шины, на которой фиксируется в момент окончания формирования остатка значение неполного частного Q в позиционно-импульсном коде, что не представляет трудностей для перевода этого кода в двоичный. Если m = 2, то неполное частное на выходе этих шин сформировано непосредственно в двоичном коде.

На фиг.1 представлена функциональная схема вычислительного устройства; на фиг. 2 - функциональная схема блока формирования частичных остатков; на фиг. 3 - вариант функциональной схемы блока умножения для случая m > 2; на фиг. 4 - функциональная схема блока дешифраций для случая m > 2; на фиг.5 - функциональная схема блока умножения для случая m = 2; на фиг.7 - вариант функциональной схемы блока умножения для случая m > 2; на фиг.8 - функциональная схема формирователя частичных остатков.

Вычислительное устройство содержит (фиг. 1) блок 1 умножения, блок 2 формирования частичных остатков и блок 3 дешифраций. Модуль Р, по которому необходимо формировать остатки, и число А, от которого необходимо сформировать остаток, подаются на входы 4 и 5 устройства соответственно. Остаток γ и неполное частное Q снимаются с выходов 6 и 7 устройства.

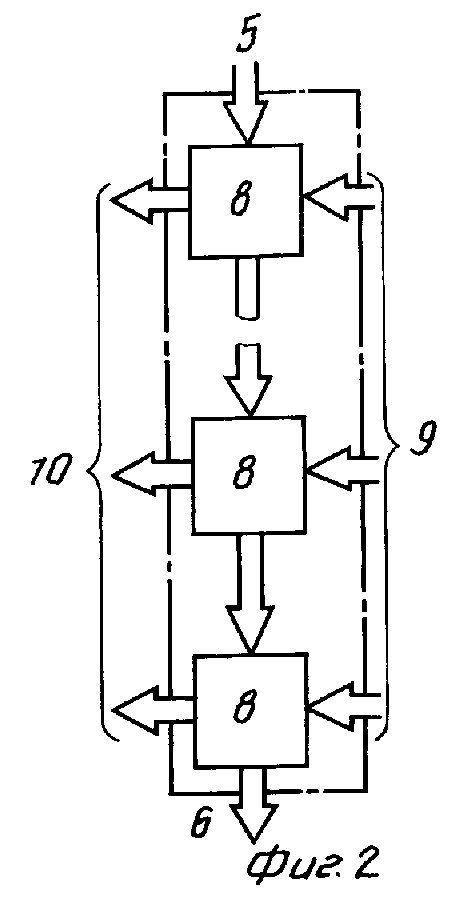
Блок 2 формирования частичных остатков (фиг.2) содержит К формирователей 8 частичных остатков, на информационные входы 9 которых подаются коды с блока 1 умножения. Выходы 10 являются информационными выходами блока. Код числа подается на вход 5, а код остатка снимается выхода 6 блока.

Первый вариант выполнения блока 1 умножения для случая m > 2 (фиг.3) содержит матрицу из (m-1) ˙K умножителей 11. Выходы 12 блока являются информационными и соединяются с соответствующими входами 9 блока 2 формирования частичных остатков.

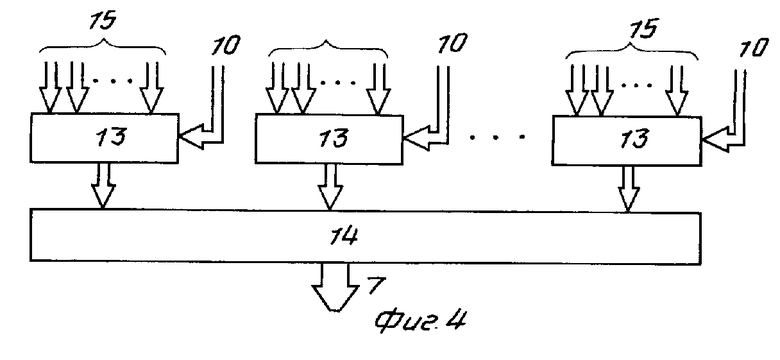
Блок 3 дешифраций для случая m > 2 содержит (фиг.4) К мультиплексоров 13 и сумматор 14, причем каждый i-й мультиплексор 13 (i = 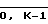) содержит (m-1) входов 15, на которых зашиты коды чисел mⁱ, 2mⁱ, 3mⁱ,...,m (m-1)ⁱ (i = ). Выход 7 блока 3 является выходом неполного частного Q устройства.

При m = 2 блок 3 дешифраций (фиг.5) содержит К входов 10, соединенных с К одноименными входами 7 блока.

Для случая m = 2 блок 1 умножения имеет (фиг.6) l+1 входов 4 (l - максимальный показатель степени представления величины модуля Р в дополнительном коде в двоичной позиционной системы счисления) и К групп выходов 12, каждая из которых содержит l+j выходов (j = ), причем i-й вход (i = ) соединен с (i+j)-м выходом j-й группы выходов блока, а первые i выходов каждой j-й группы выходов блока соединены с входом логического "0".

Второй вариант блока 1 умножения (фиг.7) содержит (m-1)K умножителей 16, объединенных в К групп по m-1 в каждой, при этом i-й умножитель j-й группы является умножителем на i x m^j.

Формирователь 8 частичных остатков (фиг.8) содержит m-1 сумматоров 17 и мультиплексор 18. Вход 19 К-го формирователя остатков является входом 5 (фиг. 2) подачи кода числа А, а выход 20 первого формирователя является выходом 6 остатка γ .

Вычислительное устройство работает следующим образом.

Рассмотрим работу вычислительного устройства, непосредственно подставляя конкретные числа на его входы.

Пусть ядро вычислений m = 2, величина К = 4. Ввиду того, что структура вычислительного устройства зависит от того, какими выбраны (при разработке принципиальной схемы устройства в зависимости от необходимых параметров) значения m и К, очевидно, что блок 2 формирования частичных остатков содержит пять формирователей частичных остатков, а блок 3 дешифраций и блок 1 умножения выполнены по схемам, представленным на фиг.5 и 6 соответственно. Формирователь 8 частичных остатков состоит из одного сумматора 17 и мультиплексора 18 согласно фиг.8. Пусть значение модуля Р = 6, а значение числа А = 100. Соответственно в двоичном коде Р = 00000110, а А = 01100100. При этом на вход 4 устройства подается дополнительный двоичный код числа Р = 11111010, а на вход 5 - двоичный код числа А = 01100100. Тогда на нулевой группе выходов блока 1 умножения (фиг.6) будет двоичный код 11111010, на первой группе выходов - дополнительный двоичный код числа 6 х 2¹ = 12 = 111110100, на второй - 6 х 2² = 24 = 1111101000, на третьей - 6 х 2³ = 48 = 11111010000 и на четвертой - 6 х 2⁴ = 96 = =111110100000. В результате на первый вход сумматора 17 с входа 19 четвертого формирователя 8 частичных остатков блока 2 поступает двоичный код числа А = 01100100, а на его второй вход - дополнительный двоичный код числа Р = 96₁₀ = 111110100000. На информационном выходе сумматора 17 образуется двоичный код 100, а на его выходе переноса появляется единица (т.е. коэффициент q₄ неполного частного Q равен единице), которая коммутирует мультиплексор 18 четвертого формирователя 8 частичных остатков таким образом, что на его выходе оказывается число, поступающее на его вход с выхода сумматора 17. Двоичный код 100 (число 4₁₀) поступает на вход третьего формирователя 8 частичных остатков блока 2. В результате на первый вход сумматора 17 с входа 19 третьего формирователя 8 поступает код 100, а на второй вход этого сумматора - код 11111010000. На выходе переноса сумматора 17 третьего формирователя 8 будет ноль, а на информационном выходе - код 11111010100. При этом коэффициент неполного частного Q, определяемый выходом переноса сумматора 17, q₃ = 0 и мультиплексор 18 коммутирует со своим выходом вход, который соединен с входом 19 третьего формирователя 8 частичных остатков, т.е. на его выходе образуется код 100. Аналогично рассуждая, видим, что на входах сумматора 17 второго формирователя 8 частичных остатков будут коды 100 и 1111101000, на выходе мультиплексора 18 второго формирователя 8 - код 100, коэффициент q₂ = 0. Далее соответственно - 1000 и 111110100, на выходе мультиплексора 17 первого формирователя 8 - 100, коэффициент q₁ = 0 и на входах сумматора 17 нулевого формирователя 8 - 100 и 11111010, коэффициент q_о = 0, а на выходе мультиплексора 18 нулевого формирователя 8 блока 2, который является выходом остатка устройства, - код 100. Итак, подан на вход 5 устройства двоичный код числа 100₁₀, а на вход 4 дополнительный код модуля Р = 6₁₀, получен на выходе 6 устройства двоичный код 100 = 4₁₀, являющийся остатком от деления числа 100 на число 6, а на выходе 7 неполное частное Q = =1000₂ = 16₁₀. Подавая на входы 4 и 5 устройства коды других модулей и других чисел, можно убедиться в правильном функционировании устройства.

Пусть теперь m = 3, К = 3. Тогда блок 2 формирования частичных остатков (фиг. 2) содержит три формирователя 8 частичных остатков, блок 1 умножения (фиг.3) содержит (m-1) = 2 строки умножителей по (К+1) = 4 в каждой. Причем впервой строке коэффициенты умножения умножителей 11 блока 1 равны 1, 3, 3, а во второй строке - 2, 3, 3. Блок 3 дешифраций (фиг.4) содержит (К+1) = =4 двухвходовых (m-1 = 2) мультиплексора и сумматора 14. НА первый информационный вход мультиплексора 13 подается двоичный код единицы, на второй вход - двоичный код двойки, на первый информационный вход первого мультиплексора 13 - двоичный код 3, на второй - 6, на первый информационный вход второго мультиплексора - двоичный код 9, а на второй - 18. Формирователь 8 частичных остатков содержит два сумматора 17 и мультиплексор 18. Пусть на вход 4 модуля устройства подан модуль Р = 5 в дополнительном двоичном коде 111111011, а на вход 5 подан двоичный код 1010011 числа 83₁₀. Тогда на выходах умножителей 11 первой строки блока 1 умножения появляются числа 5, 15, 45, представленные в своих дополнительных двоичных кодах 111111011, 111110001, 111010011 соответственно, а на выходах умножителей 11 второй строки блока 1 - числа 10, 30, 90, представленные в дополнительных кодах 111110110, 111100010, 11110100110 соответственно. Причем на второй вход первого сумматора 17 нулевого формирователя 8 воздействует дополнительный код числа 5,а на второй вход второго сумматора - числа 10, на второй вход первого сумматора 17 первого формирователя 8 - дополнительный код числа 15, а второго сумматора 17 - числа 30, соответственно, для второго формирователя 8 эти числа равны 45 и 90. На выходе первого сумматора 17 второго формирователя 8 частичных остатков образуется код 1111111001, а на его выходе переноса появляется ноль. На выходе второго сумматора 17 второго формирователя 8 образуется код 000100110, а на его выходе переноса появляется единица, которая коммутирует выход мультиплексора 18 с информационным входом, соединенным с выходом одноименного (второго) сумматора 17. Таким образом, на вход первого формирователя 8 частичных остатков поступает код 000100110, а с выхода второго формирователя 8 частичных остатков на вход блока дешифраций поступает код 01. Аналогично рассуждая, видим, что на вход нулевого формирователя 8 остатков поступает с выхода первого формирователя 8 остатков код 1000, а с второго информационного выхода формирователя 8 остатков на вход блока дешифрации поступает комбинация 11. На выходе нулевого формирователя 8 остатков, являющиеся выходом блока 2 формирования частичных остатков, появляется код 11₂ = 3₁₀, который и является остатком от числа 83 по модулю 5, а на вход блока 3 дешифраций поступает с второго выхода нулевого формирователя 8 код 01.

Рассмотрим работу блока 3 дешифраций (фиг.4). Мультиплексоры 13 осуществляют выбор необходимых коэффициентов q_jmⁱ, где q_j = 0,2 в зависимости от управляющего кода, поступающего с вторых выходов блока 2, следующим образом. Если управляющий код равен 00, то на выходе мультиплексора 13 ноль, если управляющий код равен 0,1, то на выходе нулевого мультиплексора 13 проходит код, зашитый на его первом входе, т.е. m^o˙ 1 = 1, а на выход первого мультиплексора 13 - код числа m ^o˙1 = 3. Если управляющий код равен 11 или 10, то на выходе первого мультиплексора 13 код числа m^o˙ 2 = 6, т.е. старший разряд на управляющем входе мультиплексора 13 является приоритетным. Соответственно второй мультиплексор 13 в зависимости от управляющего кода 00, 01 или 10 и 11 пропускает на свой выход чисел 0, m²˙ 1 = 9 или m² ˙2 = 18. Так как на управляющий вход нулевого мультиплексора 13 поступает код 01, первого мультиплексора 13 - код 11 и второго мультиплексора 13 - код 01, то на их выходах появляются код числа 16, являющегося неполным частным при делении 83 на 5. Мультиплексор 18 формирователей 8 частичных остатков работает аналогично мультиплексору 13 блока 3 дешифраций, т.е. с приоритетом старших разрядов на управляющем входе.

Итак, в результате работы устройства, когда на его вход 5 подан код числа 83, а на вход 4 - дополнительный код модуля Р = 5, на выходе 6 устройства образуется код остатка γ= 3, а на выходе 7 - код неполного частного Q = 16, т.е. устройство вычисляет остаток и частное от числа 83.

Непосредственной подстановкой чисел и модулей можно убедиться в правильности работы устройства для любых m и К. При увеличении m быстродействие устройства увеличивается, однако увеличиваются и аппаратурные затраты за счет увеличения количества сумматоров 17 в формирователе 8 и количества коммутируемых входов в мультиплексорах 13 блока 3 и мультиплексорах 18 формирователя 8.

Блок 1 умножения, представленный на фиг. 7, является более быстродействующим, чем тот, который представлен на фиг.3. Однако все умножители в нем выполнены на разные коэффициенты, что может оказаться неудобным при некоторых реализациях.

Таким образом, предложенное устройство обладает более широкими функциональными возможностями, так как позволяет формировать как остаток от числа, так и неполное частное.

Изобретение относится к вычислительной технике и может быть использовано в устройствах для формирования элементов конечных полей, в устройствах для формирования кодовых последовательностей, построение которых основывается на теории конечных полей, а также в арифметических устройствах, функционирующих в СОК и в арифметических сопроцессорах. Цель изобретения - расширение функциональных возможностей за счет вычисления цифр неполного частного - достигается введением блока формирования частичных остатков и блока умножения, а также их оригинальным техническим решением. 7 з.п. ф-лы, 8 ил.

1. ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, содержащий блок дешифраций, отличающееся тем, что в него введены блок формирования частичных остатков и блок умножения, причем вход модуля P в дополнительном коде устройства соединен с входом умножения, вход кода числа A устройства соединен с входом блока формирования частичных остатков, K групп выходов блока умножения K≠ log_mA_max/P, (где m - ядро вычислений, A_max - максимальное контролируемое число; P_min - минимальное используемое значение модуля) соединены с соответствующими группами входов блока формирования остатков, выходы которого соединены с входами блока дешифраций, выход которого является выходом неполного частного устройства, выход остатка которого соединен с выходом блока формирования частичных остатков. 2. Устройство по п.1, отличающееся тем, что блок формирования частичных остатков содержит K формирователей остатка (где K - разрядность неполного частного, образующегося при делении числа A на модуль P), причем первый вход i-го формирователя остатков (i = ) соединен с первым выходом (i + 1)-го формирователя остатков, второй вход j-го формирователя остатков (j = 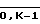) является j-й группой входов блока, вход которого соединен с первым входом K-го формирователя остатков, первый выход l-го формирователя остатка (l = 0) соединен с выходом блока, вторые выходы всех формирователей остатка являются группой выходов блока. 3. Устройство по п.1, отличающееся тем, что вариант блока умножения для случая m > 2 содержит матрицу из (m - 1) · K умножителей, причем входы (i, 1)-х умножителей матрицы (i = ) объединены и являются входом блока, выход (i, j)-го умножителя матрицы (j = )) соединен с входом (i, j +1)-го умножителя матрицы, выходы i-х умножителей в каждом из K столбцов матрицы являются p-й группой выходов блока умножения (p = ), при этом (i, 1)-й умножитель матрицы имеет коэффициент умножения i, каждый из (i, j + 1)-х умножителей матрицы имеет коэффициент умножения m. 4. 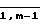Устройство по п.1, отличающееся тем, что блок дешифраций для случая m > 2 содержит K мультиплексоров и сумматор, выход которого является выходом блока, а входы соединены с выходами K мультиплексоров, управляющие входы которого являются входами блока, а на каждом i-м информационном входе (i = ) j-го мультиплексора (j = 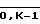) защиты коды чисел mⁱ, 2mⁱ, 3mⁱ .., (m - 1)mⁱ соответственно. 5. Устройство по п.1, отличающееся тем, что блок дешифраций для случая m = 2 содержит K входов, соединенных с K одноименными выходами блока. 6. Устройство по п.1, отличающееся тем, что блок умножения для случая m = 2 содержит (l + 1)-разрядный вход (l-максимальный показатель степени представления величины модуля p в дополнительном коде в двоичной позиционной системе счисления) и K групп выходов, каждая из которых содержит (l + j) выходов (j = ), , причем i-й вход блока (i = ) соединен с (i + j)-м выходом j-й группы выходов блока, а первые i выходов каждой j-й группы выходов блока соединены с входом логического нуля. 7. Устройство по п.1, отличающееся тем, что вариант блока умножения для случая m > 2 содержит (m - 1) · K умножителей, объединенных в K групп по (m - 1) в каждой, причем входы всех умножителей объединены и являются входом блока, выход i-го умножителя (i = ) j-й группы (j = ) является i-м выходом j-й группы блока, при этом i-й умножитель j-й группы является умножителем на i · m^j. 8. Устройство по п.1, отличающееся тем, что формирователь остатков содержит (m - 1) сумматоров и мультиплексор, выход которого соединен с выходом формирователя остатков, первый вход которого соединен с первым информационным входом мультиплексора и объединенными первыми входами всех сумматоров, вторые входы которых соединены с вторым входом формирователя остатков, j-й выход (j = ) группы выходов которого соединен с выходом переноса j-го сумматора и с j-м управляющим входом мультиплексора, (j + 1)-й информационный вход которого соединен с выходом суммы j-го сумматора.