Изобретение относится к сосудам, работающим под давлением p и может быть использовано во всех отраслях техники, где применяются такие сосуды.
Известен цилиндрический сосуд давления с эллиптическим днищем, которое при соотношении полуосей эллипса b/a = 1/2 очень близко по своей форме к днищам Бицено, равнопрочным по теории максимальных касательных напряжений. Недостатком данного днища-аналога является наличие значительных напряжений изгиба в зоне краевого эффекта.
Наиболее близким к изобретению является днище, состоящее из центральной сферической части (R, θ) и плавно сопрягаемой с ней периферийной части днища, геометрическая форма меридиана срединной поверхности которого задана уравнением
Z(r) =  F(α,ϕ) +
F(α,ϕ) + 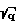 E(α,ϕ) -
E(α,ϕ) - 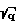 tg
tg 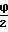
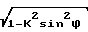 ,
,
(1) где Z - расстояние от линии сопряжения днища с цилиндрической обечайкой до рассматриваемой точки срединной поверхности днища, удаленной от оси сосуда на расстояние r;
q = 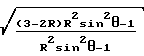 ;
;
ϕ = arctg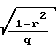 .
.
Однако такая геометрия днища имеет ряд недостатков:
1. Формула (1) cправедлива только для оболочек из изотропного материала и непригодна для композитных оболочек.
2. Так как формула (1) справедлива только для днища с постоянной толщиной стенки, а интенсивность Тi мембранных усилий Т1 и Т2
Ti= 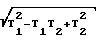 , (2) где
, (2) где
T1=  pR2; T2=R2(P-T1/R1), (3) переменна вдоль образующей днища и имеет максимум Тim, то, исходя из допустимого напряжения [ σ ], толщину днища приходится принимать равной t = Тmi/[ σ ]. Таким образом, данное днище является существенно неравнопрочным, и снизить эту неравнопрочность не представляется возможным.
pR2; T2=R2(P-T1/R1), (3) переменна вдоль образующей днища и имеет максимум Тim, то, исходя из допустимого напряжения [ σ ], толщину днища приходится принимать равной t = Тmi/[ σ ]. Таким образом, данное днище является существенно неравнопрочным, и снизить эту неравнопрочность не представляется возможным.
3. Так как формула (1) получена без учета граничных условий в стыке с цилиндрической обечайкой, то устранить краевые напряжения можно только при положительной величине U(а) для днища, согласно формуле (9) и при определенном соотношении между толщиной днища и обечайки, совершенно не согласующемся с прочностными требованиями, т.е. в сопрягаемом сечении толщина должна изменяться скачкообразно, что не всегда допустимо.
Цель изобретения - расширение эксплуатационных возможностей устройства и уменьшение массы сосуда за счет снижения напряжений в днище путем полного исключения деформации изгиба и уменьшения за счет этого толщины стенки днища.
Указанная цель достигается тем, что геометрическую форму срединной поверхности днища определяют выражением
ζ(ρ) = C1 ρ + C2(1 - ρ)  + C3 , (4)
+ C3 , (4)
где ρ = r / a; ζ = z / a; γ = b / a;
C1 = - C3 = κ C2 ; C2 = γ / (1 - κ); а - радиус обечайки;
b - высота днища;
κ - варьируемый параметр, причем 0 < κ < 1/2;
Z - расстояние от линии сопряжения днища с цилиндрической обечайкой до рассматриваемой точки срединной поверхности днища, удаленной от оси сосуда на расстояние r; а переменная толщина стенки днища равна t(r) = t(o) · 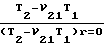 · exp{(1+ν21)J} , (5) J =
· exp{(1+ν21)J} , (5) J = 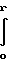
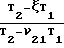 ·
· 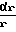 ; ζ =
; ζ = 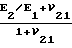 , где Т1, Т2 - мембранные усилия в днище;
, где Т1, Т2 - мембранные усилия в днище;
F1, F2, ν21 - константы анизотропии материала днища.
Полюсная точка r=0 должна быть изотропной, причем Е=Е1 и ν= ν12, чтобы обеспечить непрерывность деформации ε1, согласно (7).
Сопоставительный анализ с прототипом показывает, что заявляемый сосуд отличается формой срединной поверхности днища и законом изменения его толщины. Это позволяяет сделать этот вывод о соответствии технического решения критерию "новизна".
Сравнение заявляемого решения с другими техническими решениями показывает, что сосуды с овалоидными днищами широко известны. Однако предлагаемая геометрия днища обладает, по сравнению с известными формами днищ сосудов давления, тем преимуществом, что обеспечивает полное устранение деформации изгиба во всех точках днища, причем материал сосуда может быть как изотропным, так и ортотропным. Это позволяет сделать вывод о соответствии технического решения критерию "существенные отличия".
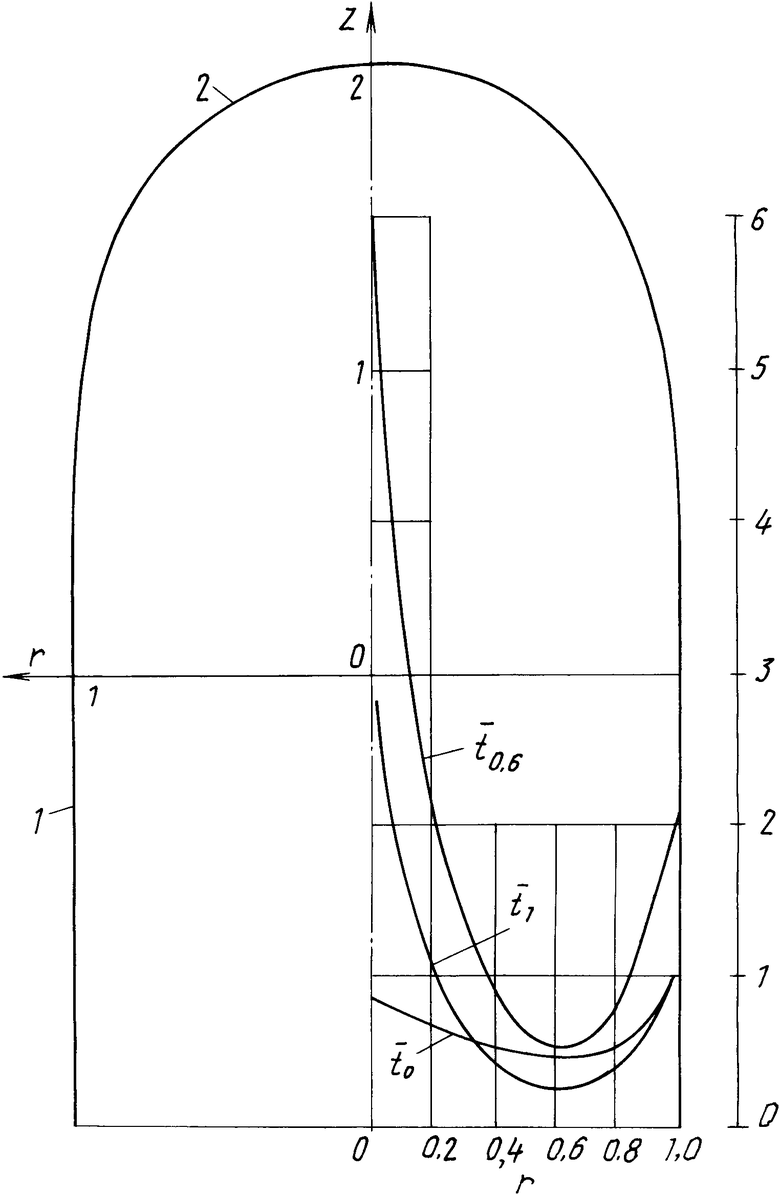
На чертеже представлена часть сосуда, продольный разрез. Сосуд содержит цилиндрическую оболочку 1 и днище 2.
Приведем алгоритм вывода соотношения (5). Условием безызгибной деформации оболочки вращения является равенство нулю угла поворота ее меридиана
V = _ 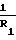
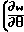 - u
- u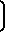 = 0 или эквивалентное уравнение
= 0 или эквивалентное уравнение (R2ε2) - (R1ε1-ε2R2)ctgθ = 0 , (6) где ε1 = (T1 - ν12T2) / E1t; ε2 = (T2 -- ν21T1) / E2t. (7)
(R2ε2) - (R1ε1-ε2R2)ctgθ = 0 , (6) где ε1 = (T1 - ν12T2) / E1t; ε2 = (T2 -- ν21T1) / E2t. (7)
С учетом (7) уравнение (6) принимает вид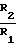 ·
· 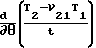 + (1+ν21)(T2-ζT1)ctgθ/t = 0 ,
+ (1+ν21)(T2-ζT1)ctgθ/t = 0 ,
(8)
где ζ = (E2 / E1 + ν21)/(1 + ν21) . Для изотропного материала аналогичное уравнение известно.
Для удовлетворения граничным условиям в сопрягаемом сечении составной оболочки целесообразно задаться некоторой формой оболочки, например в виде (4), содержащей варьируемые параметры, и найти переменную толщину днища из уравнения (8). Искомое решение имеет вид (5), причем входящие в формулу (5) силы Т1 и Т2 вычисляются по формулам (3), где R1 и R2 - главные радиусы кривизны днища, полностью определяемые его геометрией - уравнением меридиана срединной поверхности Z = Z(r), и равные
R1= -n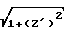 /Z′; R2= -[1+(Z′)2]3/2/ Z″ .
/Z′; R2= -[1+(Z′)2]3/2/ Z″ .
Достоинство предлагаемого днища, по сравнению с прототипом, в том, что устранить краевой эффект путем обеспечения равенства радиального смещения оболочек в сопрягаемом сечении
U= r (T2-ν21T1)/E2t (9) удается при равных толщинах оболочек в сопрягаемом сечении.
Для этого необходимо, чтобы форма днища обладала следующим свойством
R1(а) = ∞ . (10) Это условие выполняется только при определенном диапазоне значений параметра κ, а именно
0< κ <1/2 .
Очевидно, что кроме формы (4) существует множество других форм днищ, удовлетворяющих условию (10), но форма (4) является, по-видимому, аналитически наиболее простой. В то же время недостатки формы (1) объясняются именно тем, что она не удовлетворяет условию (10).
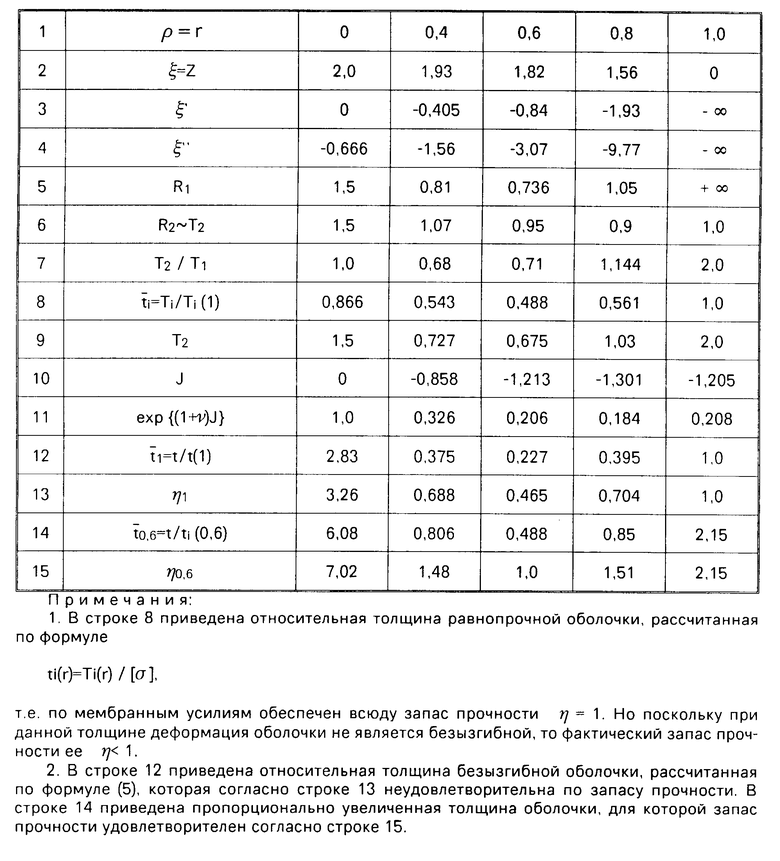
В качестве примера выполнен расчет изотропного ( ν = 0,3) днища со следующими параметрами a=1, γ=2, κ=1/3. Результаты расчета приведены в таблице. При выборе параметров γ и γκ необходимо иметь в виду, что согласно (5) толщина t>0 только при условии, что Т2- ν21Т1>0. Это означает, как следует из (9), что должно выполняться соотношение U>0. На чертеже приведена функция Z(r) (cтрока 2 табл.1), а также толщина равнопрочной оболочки (строка 8) и безызгибной оболочки t1 (cтрока 12), которая, как видно из чертежа, неудовлетворительна по запасу прочности. Удовлетворительным по запасу прочности является закон изменения толщины t0,6 (строка 14). Значительное отклонение рассчитанной оболочки от равнопрочной свидетельствует о том, что выбранные параметры γ и κ не оптимальны. Оптимизация этих параметров может быть решена только численно в каждом конкретном случае.
Выполнение сосуда давления с днищем предлагаемой формы (4), благодаря наличию двух варьируемых параметров, позволяет более полно удовлетворить техническим требованиям, предъявляемым к днищам в самых разнообразных конструктивных исполнениях сосудов; и в этом одно из главных его преимуществ, по сравнению с прототипом.
| название | год | авторы | номер документа |
|---|---|---|---|
| Переходник между двумя цилиндрическими частями сосуда давления | 1989 |
|
SU1721346A1 |
| СПОСОБ ТРАНСПОРТИРОВАНИЯ СЫПУЧИХ ВЕЩЕСТВ, АЭРОЗОЛЕЙ И КАПСУЛ | 1986 |
|
RU2037458C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КИНЕТИЧЕСКИХ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ КОМПОЗИТНЫХ МАТЕРИАЛОВ | 2020 |
|
RU2753620C1 |
| СОСУД ДАВЛЕНИЯ | 2011 |
|
RU2465511C1 |
| СПОСОБ АВТОНОМНОГО ОПРЕДЕЛЕНИЯ ОРБИТЫ И ОРИЕНТАЦИИ КОРПУСА КОСМИЧЕСКОГО АППАРАТА В ПРОСТРАНСТВЕ ПРИ ОТСУТСТВИИ АПРИОРНОЙ ИНФОРМАЦИИ | 2013 |
|
RU2542599C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ ПРОНИЦАЕМОГО ПЛАСТА | 2012 |
|
RU2492510C1 |
| БАЛЛОН ВЫСОКОГО ДАВЛЕНИЯ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ | 2011 |
|
RU2482380C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТЫ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНОГО ОБЪЕКТА | 1991 |
|
RU1829578C |
| Сосуд давления | 1984 |
|
SU1227901A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ИЗОТРОПНЫХ ЭЛЕКТРОПРОВОДЯЩИХ МАТЕРИАЛОВ | 2009 |
|
RU2419782C2 |
Использование: во всех отраслях техники, где используются сосуды, работающие под давлением. Сущность: днище сосуда выполнено в виде оболочки вращения, которая имеет геометрическую форму, определяемую выражением, представленным в описании. Днище может быть изготовлено из ортотропного материала. 2 з.п. ф-лы, 1 ил., 1 табл.
ζ(ρ) = C1ρ+C2(1-ρ)κ+C3 ,
где ρ=r / a ;
ζ = Z / a ;
γ = b / a ;
C1 = -C3 = κ C2 ;
C2 = γ / (1-κ) ;
a - радиус обечайки;
b - высота днища;
κ - варьируемый параметр, при этом 0 < κ < 1/2 ,
Z - расстояние от линии сопряжения днища с цилиндрической обечайкой до рассматриваемой точки срединной поверхности днища, удаленной от оси сосуда на расстояние r,
а переменная толщина стенки днища равна
t(r)=t(0)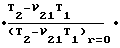 exp
exp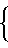 (1+ν21)J
(1+ν21)J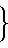 ,
,
где
J = 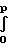
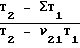 ·
· 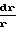 ;
;
ε = 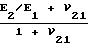 ;
;
T1, T2 - мембранные усилия в днище;
E1 , E2 , ν21 - константы анизотропии материала днища.
| Сосуд давления | 1984 |
|
SU1227901A1 |
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
Авторы
Даты
1994-09-15—Публикация
1989-07-18—Подача