Изобретение относится к бортовой системе управления космическими аппаратами для автономной (не зависящей от наземного автоматизированного комплекса управления - НАКУ) оценки орбиты и ориентации корпуса космического аппарата (КА).
Известно, что под автономным определением параметров орбиты qi,
i=1, …, 6, понимается бортовой алгоритм решения навигационной задачи на основе бортовых измерений навигационных функций L
L=f(q).
Также известно, что отсутствуют такие функции, которые позволили бы определить все шесть параметров орбиты на всем мерном интервале с учетом оскуляции ее при движении. С другой стороны, при известном поле сил, под действием которых осуществляется орбитальное движение, достаточно знать оскулирующие элементы одной точки орбиты. Но и для определения одной точки также неизвестны функции L, позволяющие определить все шесть параметров. Необходима какая-то приблизительная априорная информация о параметрах орбиты в районе точки, чтобы, опираясь на нее, рассчитать чувствительность функции (функций) L к параметрам орбиты в некоторой окрестности этой точки (опорная или априорная информация). И затем, опираясь уже на эту чувствительность, собственно измерения и априорную информацию, возможно решить задачу определения одной точки орбиты

Чаще всего за такую точку выбирается точка начала расчетов q0anp. При этом решение навигационной задачи q0уточ осуществляется на основе линеаризации (1) по Тейлору относительно опорной орбиты, т.е.
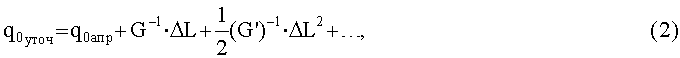
где G=||Gij|| - матрица чувствительности, элементы ее рассчитываются по опорной орбите 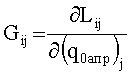
i=1, …, m; m - число измеряемых параметров,
j=1, …, n; n - количество навигационных сеансов на мерном интервале,
ΔL - вектор невязки измерений, ΔL=Lизм-Lрасч,
Lизм - вектор измеренных значений, Lизм=Lист+ξ,
Lист - значение измеренного вектора на истинной (фактической) орбите,
ξ - вектор погрешностей измерений,
Lрасч - расчетное значение измеряемого параметра на опорной орбите,
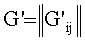
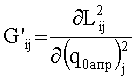
Практика решения такого рода задач показала, что в подавляющем числе случаев достаточно принять во внимание только первые два слагаемых из (2):

причем в уравнении (3) q0апр и Δq, как правило, рассчитываются итерационно: 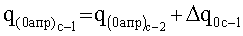
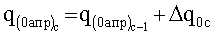
В уравнении поправок:

для уменьшения влияния погрешностей измерений необходимо иметь значительное число навигационных сеансов (во всяком случае, не меньше размерности q и, желательно, распределенных по всему мерному интервалу) и использовать какой-либо статистический фильтр (на основе метода максимума правдоподобия, наименьших квадратов, динамической фильтрации и т.п.).
Отметим, что, несмотря на то, что алгоритм динамической фильтрации позволяет находить оценки текущих точек орбиты, они также рассчитываются на основе априорной опорной информации об орбите.
Алгоритм подробно описан во многих источниках, в том числе и в [1].
Недостатком рассмотренного классического подхода к решению задачи автономной навигации, при любом составе измерителей и фильтрующем алгоритме, является необходимость ввода извне априорной информации о параметрах орбиты, что снижает уровень автономности бортового комплекса. Более того, в некоторых нештатных ситуациях, возникающих при сбое компьютера и отсутствии связи с НАКУ, аварийном пуске и выходе на неизвестную орбиту, разрушении системы ГЛОНАСС и т.п., утрачиваются данные об опорной орбите, после чего решение навигационной задачи в принципе невозможно, т.е. нарушается функционирование системы автономной навигации и ориентации.
Целью изобретения является преодоление этих недостатков, а именно - формирование оценок параметров орбиты и ориентации на основе анализа годографов осей КА, полученных в результате астроизмерений. Сформированные оценки принимаются в качестве априорной информации, далее навигационная задача решается по алгоритму (1)-(4), тем самым восстанавливается функционирование системы автономной навигации и ориентации.
Поставленная цель достигается тем, что анализируются геоцентрические годографы осей КА, рассчитанные в результате астроизмерений в жестко закрепленном на корпусе КА оптико-электронном приборе (ОЭП).
Действительно, если на каждом навигационном сеансе мерного интервала выполнить следующие действия:
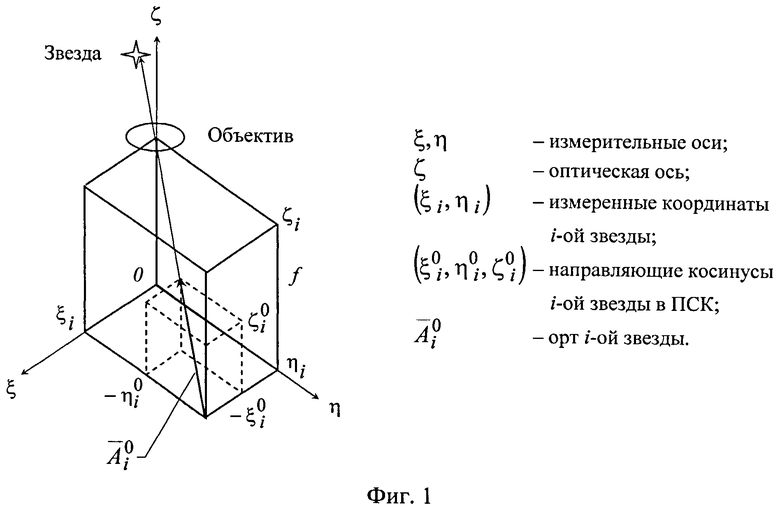
1) измерить приборные координаты видимых в ОЭП звезд и их звездные величины (фиг.1);
2) определить на основе этой информации и бортового каталога геоцентрические координаты наблюдаемых звезд;
3) рассчитать на основе последних геоцентрическую ориентацию осей ОЭП;
4) с учетом последней информации рассчитать геоцентрическую ориентацию осей КА и на этой основе сформировать годографы осей КА на всем мерном интервале,
то анализ годографов согласно разработанному алгоритму позволит рассчитать приблизительные параметры начальной точки орбиты, которые возможно принять за априорную информацию об орбите.
Алгоритмы определения геоцентрических координат наблюдаемых звезд, т.е. их распознавания, описаны в [2] и [3].
Поэтому здесь опишем алгоритмы определения геоцентрической ориентации осей ОЭП, КА и алгоритм анализа годографов осей КА с целью определения параметров опорной орбиты.
Алгоритм разработан при следующих условиях. Во-первых, предполагается, что КА, находящийся в состоянии орбитального полета, оснащен системой стабилизации, которая удерживает корпус аппарата относительно осей текущей орбитальной системы координат (ТОСК) с некоторой постоянной или меняющейся в малом диапазоне погрешностью. Эта погрешность может достигать пятнадцати градусов.
1. Определение геоцентрической ориентации осей ОЭП
Пусть в результате распознавания звезд мы имеем Q идентифицированных звезд. Принимая во внимание равенство угловых расстояний между звездами и осями ОЭП в приборной системе координат (ПСК) и геоцентрической экваториальной инерциальной системе координат (ГЭИСК) ввиду ортогональности последних, можно найти орты осей ξ, η, ζ ОЭП в ГЭИСК путем решения следующих трех систем Q линейных уравнений с тремя неизвестными:
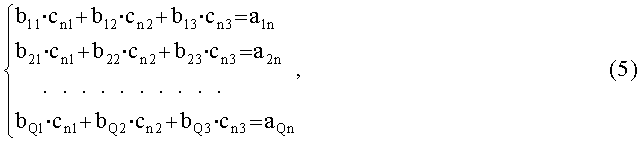
где 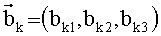
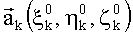
k=1, …, Q;
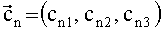
n=1 отвечает оси %, n=2 - оси η и n=3 - оси ζ (фиг.1).
Каждая из систем вида (5) решается методом наименьших квадратов, ее решением является такой вектор 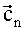
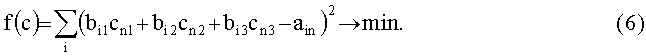
После расчета частных производных функции (6), принимая во внимание, что 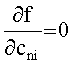

При этом В=(Bjk), 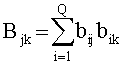
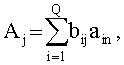
Из (7), после обращения матрицы B, находится искомый вектор:

2. Определение ориентации К А в ГЭИСК
Задача определения направляющих векторов x0, y0, z0 осей связанной системы координат (ССК) в ГЭИСК решается следующим образом.
Из векторов 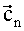

которая является матрицей перехода из ГЭИСК в ПСК.
По известным значениям углов крепления ОЭП на корпусе КА формируется матрица перехода из ССК в ПСК
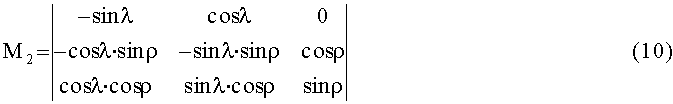
Матрица

является матрицей перехода из ГЭИСК в ССК. Искомые векторы x0, y0, z0 являются соответственно первой, второй и третьей строками этой матрицы.
Очевидно, что точность расчетов базисных векторов ПСК и ССК, согласно (5)-(11), определяется только погрешностями ОЭП и не зависит от орбиты, погрешностей системы стабилизации КА и углов закрепления ОЭП на корпусе КА, что подтверждается и опытом моделирования.
3. Определение оценок орбиты и погрешностей системы стабилизации на основе анализа годографов осей КА
Под годографом оси КА понимается массив ортов системы координат Xсв, Yсв, Zсв, связанной с корпусом КА (связанная система координат - ССК), при этом в случае нулевых погрешностей системы стабилизации ось Xсв (продольная) совпадает с направлением трансверсали (ось Т ТОСК), ось Zсв (боковая) направлена по радиус-вектору (ось S ТОСК) и ось Yсв (также боковая), дополняющая систему до правой, - по бинормали к плоскости орбиты (ось W ТОСК).
Задача формирования оценок оскулирующих элементов (ОЭ) орбиты: большой полуоси (а), эксцентриситета (е), наклонения плоскости орбиты (i), аргумента восходящего узла ( Ω), аргумента перигея (ω) и истинной аномалии (θ) - решается на основе анализа годографов осей Yсв и Zсв.
Идея алгоритма состоит в том, что, начиная с некоторого момента времени, через равные промежутки в ОЭП производятся измерения координат звезд, распознавание этих звезд и расчет векторов направляющих косинусов осей ПСК и ССК. При наблюдении годографа оси Zсв (назовем его годограф 1) исходим из того, что направления этой оси в начале и конце витка приблизительно совпадут, что позволяет зафиксировать завершение витка и получить оценки периода и большой полуоси орбиты. Годограф оси Yсв (годограф 2) позволяет определить примерный вектор нормали к плоскости орбиты, который однозначно определяет оценки наклонения и аргумента восходящего узла. Из дальнейших исследований и преобразований годографа 1 можно получить оценки эксцентриситета, аргумента перигея и истинной аномалии.
Алгоритм расчетов состоит в следующем. Выбирается момент времени t1 (определяемая точка), для которого вырабатываются оценки ОЭ и который принимается за начало мерного интервала (начало витка). От этого момента ведется относительный отсчет времени. Измерения проводятся с установленным шагом dt.
3.1 Формирование годографов, фиксирование конца витка
На каждом измерительном сеансе с номером j в момент времени tj, tj=t1+(j-1)·dt, после измерений в ОЭП, распознавания, расчета ориентации ОЭП и КА, годографы 1 и 2 пополняются геоцентрическими ортами осей Zсв и Yсв (обозначим их 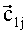
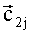
Пусть

где αj - угол между начальным и текущим положением направления оси Zсв. Измерения завершаются в момент t2, когда угол αj уменьшается (идет вторая половина витка) и достигает своего минимума, т.е. выполняется условие

При этом можно сделать вывод о завершении витка. Обозначим через N номер сеанса, на котором выполняется условие (13), тогда t2-tN.
Время T=t2-t1 принимается в качестве начальной оценки периода орбиты, которая впоследствии уточняется.
3.2. Оценки параметров ориентации плоскости орбиты
Оценки наклонения (i) и аргумента восходящего узла (Ω) однозначно определяются вектором нормали 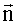
В идеальном случае, при нулевых погрешностях системы стабилизации, элементы этого годографа практически идентичны на всех измерительных сеансах и совпадают с искомым вектором 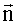
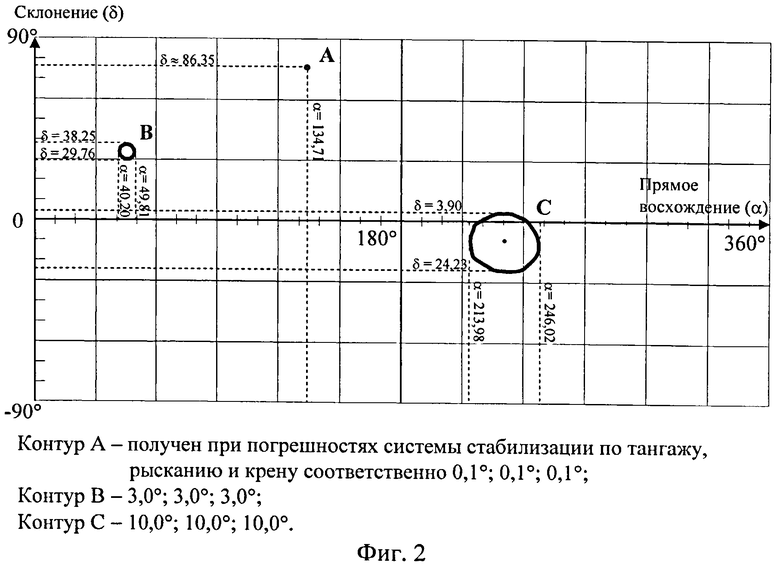
В реальных условиях, при наличии постоянных или изменяющихся в малом диапазоне погрешностей стабилизации, орт оси Zсв описывает конус, направление в центр основания которого и есть искомый вектор нормали, а годограф 2 представляет собой замкнутую кривую, близкую к окружности (фиг.2) с центром α0, δ0. В простейшем случае, при постоянных погрешностях системы стабилизации, центр этой окружности может быть определен как среднее наименьшего и наибольшего значений соответствующих координат, а при наличии колебаний в погрешностях - через метод наименьших квадратов - как центр окружности, наилучшим образом аппроксимирующей линию годографа.
При этом нормаль 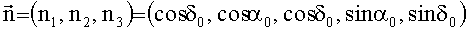
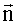
Направление в точку восходящего узла (фиг.3) определяется векторным произведением

где 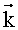
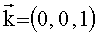
3.3. Оценки периода и большой полуоси
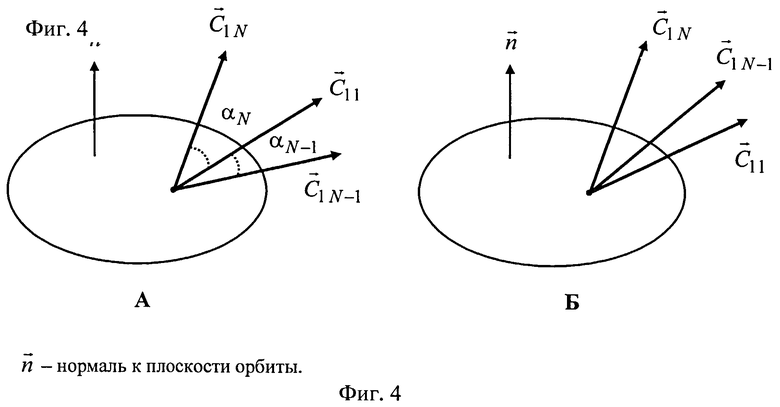
На фиг.4 изображены два возможных варианта взаимного расположения векторов 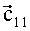
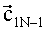
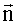
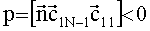
Далее в обоих вариантах рассчитывается поправка 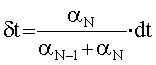
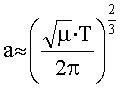
3.4. Формирование оценки эксцентриситета
Согласно второму закону Кеплера радиус-вектор орбиты (вектор S) в течение витка за равные промежутки времени заметает равные площади. Моделирование показало, что это справедливо и для годографа оси Zсв при погрешностях системы стабилизации до 15° по каждой из осей.
При эксцентриситете орбиты, большем нуля, угол между соседними элементами годографа 1 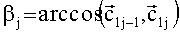
в зависимости от j.
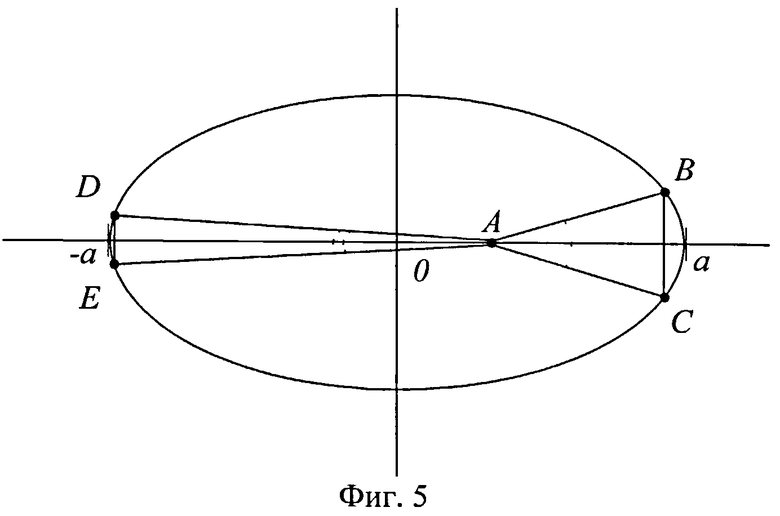
Пусть

На фиг.5 представлен фрагмент движения оси Zсв в идеализированном случае, при малых погрешностях системы стабилизации. Направляющие векторы прямых AB, AC, AD и AE есть положения вектора 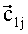

Если h - высота ΔABC, H - высота ΔADE, то из (16) следует, что 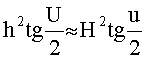

Из того, что u<U, следует: 0<q<1. Из свойств эллипса
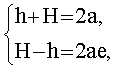
отсюда 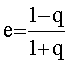
3.5. Формирование оценок аргумента перигея и истинной аномалии
Пусть максимум угла βj, определенного в (15), достигается при j=j', при этом в качестве начальной оценки направления в точку перигея принимается вектор
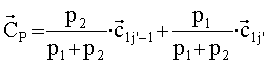
где 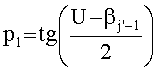
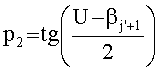
Этот вектор для орбит с эксцентриситетом e>0,01 уточняется путем формирования аппроксимирующего полинома третьей степени f(t)=at3+bt2+ct+d, минимизирующего сумму квадратов невязок 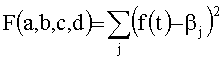
Из условия 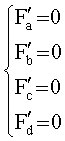
Применение аппроксимации для околокруговых орбит не приносит положительного эффекта и поэтому не производится.
Оценка аргумента перигея формируется как угол между направлениями в точку восходящего узла и в точку перигея (фиг.3), т.е.
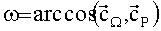
Оценка истинной аномалии зависит от момента времени tj, на которое этот параметр формируется, и рассчитывается как функция Fθ вектора 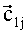

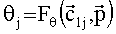
1) первоначально полагается

2) далее рассчитывается смешанное произведение векторов

3) и оценка истинной аномалии может быть уточнена в зависимости от его знака:

Для определяемой точки орбиты (t=t1) начальное значение оценки истинной аномалии 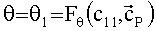
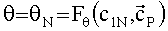
Известным образом по сформированным оскулирующим элементам определяемой точки орбиты рассчитаем ее радиус-вектор 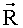
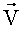
Отметим, что на точность оценок элементов a, e, i, Ω наличие погрешностей стабилизации корпуса аппарата в диапазоне до 15° не оказывает существенного влияния, но оценки ω и θ зависят от этих погрешностей, поэтому их необходимо определять и учитывать при построении оценок ω и θ.
3.6. Уточнение оценок аргумента перигея и истинной аномалии на основе формирования оценок погрешностей системы стабилизации
Разработан следующий итеративный алгоритм, сглаживающий влияние погрешностей стабилизации.
Шаг А. Расчет оценок погрешностей стабилизации.
На каждой точке мерного интервала (j=1, …, N) формируются матрицы перехода Gj (из ГЭИСК в ССК) и Hj (из ГЭИСК в ТОСК): строки матрицы Gj состоят из ортов осей ССК в ГЭИСК, при этом орты осей Zсв и Yсв - элементы годографов 1 и 2 соответственно (векторы 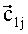
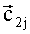
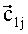

Отсюда получаем матрицу перехода из ТОСК в ССК (Sj):
Sj=Gj∗Hj T.
С другой стороны, элементы этой матрицы выражаются через углы тангажа (ϑj), рысканья (ψj) и крена (γj) [1, с.135]:
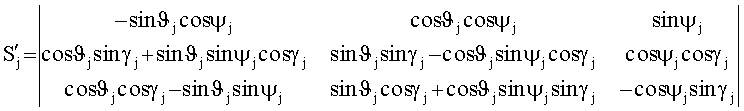
Из элементов матрицы Sj и рассчитываем 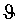
Окончательные оценки 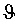
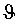
Шаг Б. Расчет матрицы поворота вокруг осей ТОСК.
Используя полученные значения углов 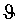
Матрица поворота MR=R_2(γ)∗R_1(ψ)∗R_3(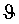
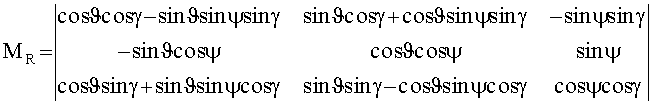
Шаг В. Поворот векторов 
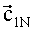
Над каждым из векторов 
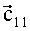
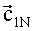
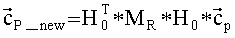
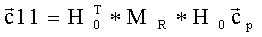
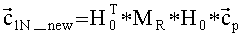
где матрица Hj из (21) и полагается H0=H(θ=0).
Шаг Г. Уточнение аргумента перигея и истинной аномалии.
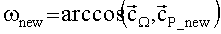
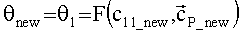
Дополнительно определяем 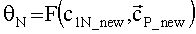
Шаг Д. Расчет поправок.
Рассчитаем радиус-вектор Rnew и вектор скорости Vnew при ω=ωnew, θ=θnew, с учетом определенных a, e, i, Ω. Определяем 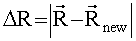
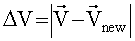
Если ΔR> εR и ΔV>εV (εR,εV - малые числа), то итеративный процесс завершается, в противном случае повторяются шаги А-Д.
Опыт моделирования показал, что, во-первых, с применением вышеописанного итеративного алгоритма точность определения орбиты повышается в разы, а во-вторых, алгоритм сходится, и количество итераций обычно не превышает 5-7.
Новизна предложения заключается в том, что неизвестные оценки опорных параметров орбиты и ориентации корпуса КА формируются на основе только астроизмерений, без использования каких-либо внешних источников информации, в том числе и средств спутниковых радионавигационных систем. Кроме того, применение предлагаемого автономного способа получения опорных оценок орбиты и ориентации исключает произвол в определении этих значений традиционным способом, что положительно влияет на устойчивость решения навигационной задачи.
Экспериментальное исследование предлагаемого способа проводилось на основе компьютерной модели, разработанной в 34 отделе военного института (НИ) ВКА имени А.Ф. Можайского. Моделирование осуществлялось при постоянных погрешностях стабилизации (до 15° по каждому из каналов: тангаж, рыскание и крен), при погрешности измерений в ОЭП от 0,1” до 30” и шаге между измерительными сеансами в 300 секунд. При этом число измерительных сеансов лежало в зависимости от орбиты в пределах от нескольких десятков до нескольких сотен.
В таблице 1 приведены результаты моделирования разработанного способа при среднеквадратической погрешности измерений в 0,5", распределенных по нормальному закону, для различных орбит и погрешностей системы стабилизации. Выработанные данным способом оценки орбиты и ориентации использовались в качестве априорных значений для последующего решения задачи навигации и ориентации способом виртуальных измерений зенитных расстояний звезд [4]. В итоге получены такие же высокие результаты по определению орбиты (единицы метров по положению и десятые доли миллиметров в секунду по скорости) и определению ориентации (единицы угловых секунд), какие приведены в описании патента [4].
Таким образом, анализ результатов моделирования показывает, что точности полученных предложенным способом оценок орбиты и ориентации корпуса аппарата позволяют принять эти оценки за опорные значения и тем самым восстановить функционирование системы автономной навигации и ориентации. Результаты моделирования подтвердили работоспособность предлагаемого способа и реальность достижения цели изобретения.
Источники информации
1. Кузнецов В.И., Данилова Т.В. Автоматизированная система исследований методов и алгоритмов автономной навигации и ориентации космических аппаратов. Учебное пособие, СПб., ВКА имени А.Ф. Можайского, 2006 г., 322 с, илл.
2. Кузнецов В.И., Данилова Т.В. Алгоритмы распознавания “рабочих” звезд по звездному полю, СПб., Известия ВУЗов, Приборостроение, 2003 г., т.46, №4, с.16-23.
3. Кузнецов В.И. Автоматизированная система научных исследований методов и алгоритмов автономной навигации и ориентации космических аппаратов. Монография, СПб., ВКА имени А.Ф. Можайского, 2010 г., 453 с, илл.
4. Патент на изобретение №2454631 “Способ автономной навигации и ориентации космических аппаратов на основе виртуальных измерений зенитных расстояний звезд”.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УДЕРЖАНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСИНХРОННОЙ 24-ЧАСОВОЙ ОРБИТЕ | 2013 |
|
RU2535353C2 |
| СПОСОБ МОНИТОРИНГОВОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2013 |
|
RU2558959C2 |
| АВТОНОМНАЯ БОРТОВАЯ СИСТЕМА УПРАВЛЕНИЯ КОСМИЧЕСКОГО АППАРАТА ГАСАД-2А | 2005 |
|
RU2304549C2 |
| СПОСОБ АВТОНОМНОЙ НАВИГАЦИИ И ОРИЕНТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ НА ОСНОВЕ ВИРТУАЛЬНЫХ ИЗМЕРЕНИЙ ЗЕНИТНЫХ РАССТОЯНИЙ ЗВЕЗД | 2010 |
|
RU2454631C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ПОЛОЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА В ПРОСТРАНСТВЕ С ИСПОЛЬЗОВАНИЕМ ОРБИТАЛЬНОГО ГИРОКОМПАСА | 2012 |
|
RU2509690C1 |
| СПОСОБ АВТОНОМНОЙ НАВИГАЦИИ И ОРИЕНТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ | 2006 |
|
RU2318188C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2018 |
|
RU2703696C1 |
| БЕСПЛАТФОРМЕННЫЙ ОРБИТАЛЬНЫЙ ГИРОКОМПАС С ПРОИЗВОЛЬНОЙ КУРСОВОЙ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА | 2011 |
|
RU2488774C1 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ЦЕНТРА МАСС КОСМИЧЕСКОГО АППАРАТА | 2011 |
|
RU2487823C1 |
| СПОСОБ ПЕРСОНАЛЬНОЙ АВТОНОМНОЙ НАВИГАЦИИ | 2013 |
|
RU2523753C1 |
Изобретение относится к системам автономной навигации и ориентации космического аппарата (КА). Технический результат - расширение функциональных возможностей. Для этого осуществляют формирование оценок оскулирующих элементов орбиты и углов ориентации КА относительно осей текущей орбитальной системы координат. Эти оценки определяются на основе анализа геоцентрических годографов осей КА, полученных на основе обработки результатов измерений в жестко закрепленном на корпусе КА оптико-электронном приборе координат звезд и их звездных величин. Полученные оценки используются в качестве априорной информации при решении задачи навигации и ориентации на борту КА. При этом восстанавливается возможность функционирования системы автономной навигации и ориентации при аварийном пуске КА, либо при возникновении других нештатных ситуаций, связанных с потерей априорной (опорной) информации. Тем самым повышаются степень автономности и уровень надежности функционирования бортового комплекса управления, повышается степень боевой устойчивости и вероятности выполнения полетного задания. 5 ил., 1 табл.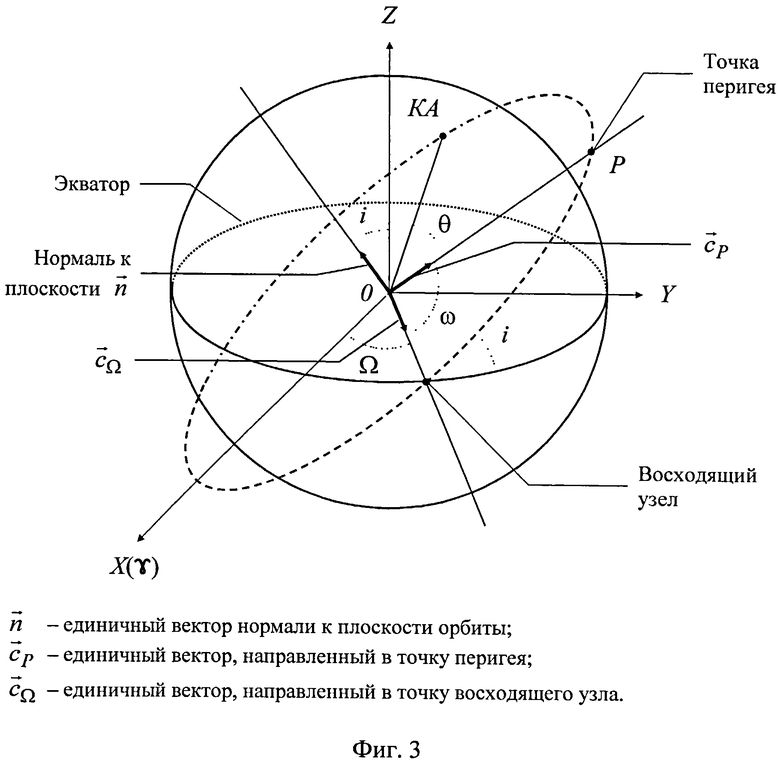
Способ автономного определения орбиты и ориентации корпуса космического аппарата (КА) в пространстве при отсутствии априорной информации, отличающийся тем, что в каждом навигационном сеансе измеряют с помощью жестко закрепленного на корпусе КА оптико-электронного прибора координаты звезд и их звездные величины, по этой информации с использованием бортового каталога определяют геоцентрические координаты звезд, на основе которых рассчитывают геоцентрическую ориентацию осей КА, формируют за весь мерный интервал годографы осей КА, путем анализа последних рассчитывают приблизительные параметры орбиты и ориентации, принимаемые за априорную (опорную) информацию, после чего восстанавливают возможность функционирования системы автономной навигации и ориентации.
Авторы
Даты
2015-02-20—Публикация
2013-06-18—Подача