Изобретение относится к технике транспортирования газом сыпучих веществ, аэрозолей, а также сформированных капсул. Может быть использовано в различных областях техники, например взамен гидротранспорта смесей, вместо ж/д или речного транспорта при доставке сыпучих и пылящих материалов на неограниченные расстояния при доставке зерна с поля на элеваторы, при транспортировке муки на большие расстояния и т.д.
Известен способ, по которому между двух концентрически расположенных труб подан воздух, при этом по внутренней эластичной трубе течет материал. Достигнуто увеличение дальности подачи. Однако способ не позволяет транспортировать на большие расстояния, т.к. необходимо прикладывать параллельно питающий воздуховод, что сложно. Скорость транспорта ограничена. Невозможно создать транспортирующее силовое поле.
Известен способ транспортирования вязких электропроводных материалов, который обладает недостатками: материал должен быть электропроводным и вязким, значительны затраты электроэнергии.
Наиболее близким (прототипом) является способ транспортирования сыпучих веществ, реализованный во всасывающе-нагнетательной установке для пневмотранспорта сыпучих материалов. Благодаря сочетанию всасывающего и нагнетательного способов транспорта увеличивается дальность транспортирования. Установка обладает существенными недостатками. Дальность нагнетательной установки ограничена 1-1,5 км из-за невозможности создания экономичного режима. Потери давления в трубопроводе при его большой разности определяются уравнением
P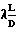 ·
· 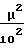 RT Анализ уравнения и расчеты по нему показывают, что при разумных диаметрах трубопровода и при давлении в конус его, отвечающем уравнению Сен-Венана v
RT Анализ уравнения и расчеты по нему показывают, что при разумных диаметрах трубопровода и при давлении в конус его, отвечающем уравнению Сен-Венана v  при минимальной скорости истечения газа в соответствии с уравнением vВ.К= C
при минимальной скорости истечения газа в соответствии с уравнением vВ.К= C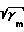 + βL
+ βL
Транспортирование материала всасывающим способом обладает еще меньшими возможностями. Недостатки этого способа негерметичность системы, неорганизованный ввод газовой смеси и материала, невозможность создания управляемого режима, ограниченная скорость потока, незначительная дальность транспортирования.
Цель изобретения повышение эффективности трубопроводного транспорта при перемещении материалов, создание условий, расширяющих возможности трубопроводного транспорта с использованием в качестве силового поля энергии газового потока. Цель предполагает расширение областей применения трубопроводного транспорта, замену других видов транспорта.
Поставленная цель в новом способе достигается следующими приемами. Транспортный трубопровод по всей его длине от места ввода материала и газа до места его выгрузки включительно изолируют и герметизируют от внешней среды, затем газовую среду в нем откачивает на заданный уровень вакуума. Давлением газовый поток через сопло Лаваля и вещество или капсулы через дозирующее устройство раздельно вводят в организованное (рабочее) для транспортирования пространство. Затем регулируют и далее поддерживают откачными устройствами заданный по длине транспортного трубопровода уровень вакуума, перемещают вещество, аэрозоли или капсулы под действием разряженного газового потока в вязкостном, вязкостно-молекулярном или молекулярном режиме в каждом самостоятельно или одновременно в нескольких в указанной последовательности в любом варианте.
Данное решение отличается от известного следующими признаками:
наличием изоляции и герметизации рабочего пространства, т.е. места ввода газового потока, вещества, транспортного трубопровода, соединительных трубопроводов, арматуры, пространства для осаждения вещества, блока откачных устройств. Изоляция достигается конструктивным исполнением устройства. Герметизация в месте ввода газового потока достигается путем "запирания" трубопровода газовым потоком в критическом сечении сопла Лаваля вследствие обеспечения истечения газа в нем со скоростью не ниже местной скорости звука;
раздельным вводом газа и материала в транспортный трубопровод, дозирующим устройством, расположенным на некотором расстоянии от критического сечения сопла Лаваля над транспортным трубопроводом. В организованном для дозирования пространстве уровень вакуума с учетом наличия дозируемого материала должен соответствовать значению его в транспортном трубопроводе в месте соединения дозирующего устройства. При незначительных уровнях разрежения в транспортном трубопроводе герметизация его от накопительной емкости для дозируемого материала может быть осуществлена за счет конструкции дозирующего устройства и поддержания на необходимом уровне материала в накопительной емкости. Герметизация на выходе транспортного трубопровода обеспечивается путем присоединения к концу трубопровода организованного пространства для разделения газа и веществ;
герметизация трубопровода обеспечивается его конструкцией;
откачкой газовой среды. Герметичность рабочего пространства создает условия для возможности откачки системы на любой заданный наперед уровень. Ввод расчетного газового потока при наличии герметичности системы и поддержании на заданном расчетном уровне вакуума создает условие для его прохождение в транспортном трубопроводе при скорости, превышающей значение числа Маха. Дальность перемещения газового потока растет с повышением разрежения и ростом величины газового потока. Расчеты показывают, что относительно легко может быть построен режим в трубопроводе протяженностью 150-200 км при среднем диаметре 30 см, чтобы обеспечить всю годовую потребность Нижегородской области, например, в цементе;
вводом газового потока через сопло Лаваля при скорости не ниже местной скорости звука. Именно при этом условии становится возможным герметизировать систему и одновременно ввести заранее определенный расчетный поток
раздельным вводом в транспортный трубопровод газового потока и вещества. Именно раздельный ввод создает условия запирания трубопровода, без которого невозможна откачка системы или рабочего пространства. В существующих системах применяется совместный ввод газового потока и вещества в транспортный трубопровод после смесительной камеры. Кроме того, в существующих системах невозможна также и откачка смесительной камеры, т.к. в ней предусмотрена неуправляемая аэрация материала; суживающееся сопло не работает в режиме запирания"; возможен неуправляемый приток газа через систему подачи материала.
По мере заполнения трубопровода веществом и газовой смесью осуществляется регулирование режима, который поддерживают откачными устройствами по длине транспортного трубопровода. Необходимость регулирования режима вытекает из условия получения наиболее экономичных характеристик течения смеси, которые зависят от массы перемещаемого материала, изменяющейся по мере ее ввода.
Перемещение вещества осуществляется под действием разреженного газового потока в разреженной среде. Режим газового потока выбирается из экономических соображений вязкостным, вязко-молекулярным или молекулярным в зависимости от конкретных условий переноса массы. Особенность использования режимов состоит:
во-первых, в исчезновении трения переносимой массы о стенки канала, в особенности в разреженной среде. Явление резко увеличивается в разреженных газах вследствие роста скорости скольжения и поперечного градиента скорости; во-вторых, в уменьшении коэффициента трения газа по мере роста потока и увеличения вакуума, доказывается ниже; в-третьих, в исчезновении турбулентности потока при Re < 2200, Кn << 1 образовании ламинарного течения, уменьшении энергетических затрат на его создание при Kn > 10-2, в-четвертых, в снижении абсолютного значения величины газового потока и упрощении отделения газа от вещества.
Сущность изложенного способа утверждается следующим. Изоляция и герметизация рабочего пространства обеспечивается путем устройства транспортного, например, стального трубопровода на необходимую длину. Ввод вещества и его вывод из трубопровода обеспечиваются путем присоединения к нему известного устройства, как сообщалось ранее. Новым является решение вопроса ввода газового потока. Неорганизованный ввод потока и вещества один из недостатков известных систем. Ввод потока может быть осуществлен с использованием суживающихся, расширяющихся и сопл Лаваля. Применение сопла Лаваля при определенных условиях режима работы и геометрических параметрах позволяет "запереть" входное сечение трубопровода газовым потоком в критическом сечении. Режим работы сверхзвукового сопла Лаваля может быть построен при расчетном и нерасчетном расширении. Нерасчетное расширение газового потока характеризуется значением противодавления за пределами выходного среза сопла Рпр менее фиксированного расчетного значения РII. Анализ второго закона термодинамики в приложении к течению в сопле Лаваля с нерасчетным расширением показывает, что такой режим работы сопла отвечает случаю 1-му, когда на входе в сопло число Маха М < 1, а за критическим сечением М > 1. При этом РпрI < РIII, сход волн разрежения наблюдается с кромок сопла, а работа сопла похожа на случай течения без трения.
Анализ режима работы сопла показывает, что указанный режим может быть зафиксирован тремя условиями: 1. 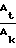 > 0,5 2. Отрицательным значением изменения энтропии
> 0,5 2. Отрицательным значением изменения энтропии
Sк-Sн= Rln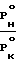 Rln
Rln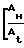
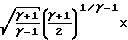
× Wк(1-W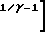 Rln
Rln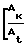 ·
· 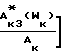 < 0
< 0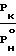
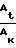
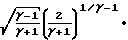
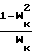 3. Wk < W*, где для из энтропического случая
3. Wk < W*, где для из энтропического случая
Wк=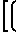 1-
1- 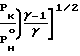
W*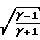 Основные расчетные характеристики сопла могут быть получены из условия максимальной тяги:
Основные расчетные характеристики сопла могут быть получены из условия максимальной тяги: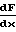 (Pк-Pпр)
(Pк-Pпр)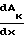
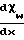 0 которое после ингибирования приводится к виду
0 которое после ингибирования приводится к виду ·
· 

или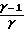 ·
· 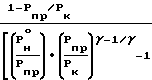
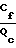 При ламинарном течении в круглом канале
При ламинарном течении в круглом канале
Re 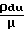
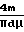 а для турбулентного течения по каналу круглого поперечного сечения с гладкими стенками определяется уравнением Кармана
а для турбулентного течения по каналу круглого поперечного сечения с гладкими стенками определяется уравнением Кармана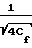 2log
2log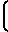 Re
Re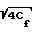
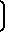 -0,8
-0,8
Условие запирания определяется величиной максимальной приведенной скорости Wн или максимального числа Маха Мн. Течение возможно, если величина Ак/At задана и ее значение меньше или равно приведенной площади, вычисленной по уравнению
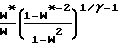 =
= 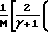 1+
1+ 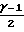 M
M Течение возможно, если Wн ≅ (Wн)max или Мн ≅ (Мx)max, где
Течение возможно, если Wн ≅ (Wн)max или Мн ≅ (Мx)max, где
W 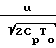 , a Umax=
, a Umax= 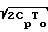
M2= 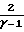 ·
· 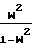 Условие запирания наступает в недорасширенном сопле, когда скорость потока в суженном сечении принимает значение скорости звука, при этом критическое отношение давлений
Условие запирания наступает в недорасширенном сопле, когда скорость потока в суженном сечении принимает значение скорости звука, при этом критическое отношение давлений 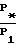 зависит от К и выражается Ψкр=
зависит от К и выражается Ψкр=  Для воздуха K=1,4 ϑ= 0,53. Настоящее состояние течения отвечает случаю 4. Переход в область недорасширенного режима течения, когда значения Рно и Рпрстановятся независимыми, описан выше тремя условиями. Случай 5 отвечает переходному режиму, когда РII Рпр. В этом случае
Для воздуха K=1,4 ϑ= 0,53. Настоящее состояние течения отвечает случаю 4. Переход в область недорасширенного режима течения, когда значения Рно и Рпрстановятся независимыми, описан выше тремя условиями. Случай 5 отвечает переходному режиму, когда РII Рпр. В этом случае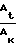 0,5; Sк-Sн< 0 и Wк> W*
0,5; Sк-Sн< 0 и Wк> W*
Таким образом, задаваясь значением Рпр и Рно, а также значением Сfи Сс, определяем из уравнения максимальной тяги величину 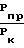 . Затем находим значение Рк. Число Маха определяется для из энтропического течения
. Затем находим значение Рк. Число Маха определяется для из энтропического течения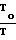
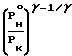 = 1+
= 1+ 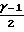 · μ2=
· μ2= 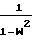 Далее определяем
Далее определяем 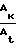
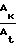 CmX(γ)
CmX(γ)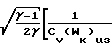 Cv(Wк)
Cv(Wк)
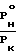 Определяем коэффициент тяги
Определяем коэффициент тяги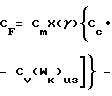 C
C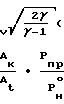 Wк)uз+
Wк)uз+ 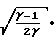
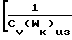
(Wк)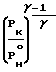 По величине CF
По величине CF
CF= 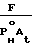
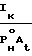 +
+ 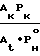
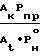
(Iк) (Iк)изCm˙Cv˙Cc где
(Iк)из= m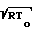 ·
· 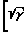 · M
· M PA[γM2] где Р Рк, А Ак, М2 Мк2. Находим Iк, а затем At По уравнению
PA[γM2] где Р Рк, А Ак, М2 Мк2. Находим Iк, а затем At По уравнению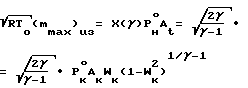 PкAк
PкAк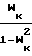 определяем расход газа.
определяем расход газа.
Более точный расчет строится на детальном анализе работы сопла Лаваля с учетом изменения CF по длине сопла на основе дифференциального уравнения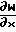
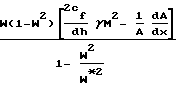 Таким образом, режим в сопле Лаваля считается построенным, а критическое сечение запертым, что создает условия для откачки газа.
Таким образом, режим в сопле Лаваля считается построенным, а критическое сечение запертым, что создает условия для откачки газа.
Выявленное выше условие запирания сопла Лаваля газовым потоком не является достаточным для оценки явления. Не менее важным для правильного вывода становится знание условий движения многофазной системы в горле. Для адиабатического процесса без трения на стенках скорость звука в смеси может быть записана в форме:
Mg2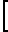 1+
1+ 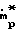
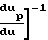 а для твердых частиц
а для твердых частиц
M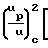 1+
1+ 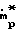
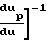 Уравнения свидетельствуют о том, что в горле обе фазы имеют дозвуковые скорости: смесь газа с твердыми частицами является диссипативной системой даже при отсутствии трения на стенках. С учетом трения на стенках уравнения движения в одномерном случае принимает вид:
Уравнения свидетельствуют о том, что в горле обе фазы имеют дозвуковые скорости: смесь газа с твердыми частицами является диссипативной системой даже при отсутствии трения на стенках. С учетом трения на стенках уравнения движения в одномерном случае принимает вид: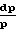 (
( T)
T)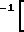 u
u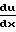 +
+ 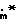 u
u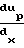 + 2
+ 2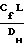 u
u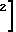 Число Маха газовой фазе в горле равно
Число Маха газовой фазе в горле равно
Mg2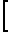 1+
1+ 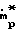
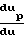 + 2
+ 2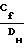 u
u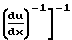 Клигель и Никерсон теоретически определили число Маха газа в горле, вычисленное по скорости звука в газе, которое оказалось равным 0,8.
Клигель и Никерсон теоретически определили число Маха газа в горле, вычисленное по скорости звука в газе, которое оказалось равным 0,8.
Сказанное позволяет сделать важный вывод. Во-первых, газовая фаза в смеси с веществом в сопле Лаваля не достигает скорости звука. Во-вторых, нельзя обеспечить запирание трубопровода вводом через сопла Лаваля, эжектированием или другим способом газового потока совместно с веществом. Раздельный ввод газового потока и вещества непременное условие герметизации рабочего пространства.
При наличии герметизации рабочего пространства уровень разрежения в системе будет определяться величиной суммарного газового потока по длине трубопровода. Величина этого потока будет зависеть от роли связанных газов. Адсорбция и десорбция газов являются результатом слабых (дисперсионные силы Ван-дер-Ваальса) и сильных (валентные силы) взаимодействий частиц газа с поверхностью, которая характеризуется энергией связи по уравнению
W 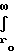 F(r)dr При расчете крионасосов следует иметь ввиду, что величина скорости адсорбции к чистой поверхности определяется уравнением
F(r)dr При расчете крионасосов следует иметь ввиду, что величина скорости адсорбции к чистой поверхности определяется уравнением
SA= 3,65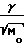 ·
· 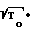 A, а величина потока из уравнения I 3,65
A, а величина потока из уравнения I 3,65 ·
· 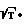 P·A Время пребывания частиц на поверхности описывается уравнением Френкеля:
P·A Время пребывания частиц на поверхности описывается уравнением Френкеля:
τпр= τпрo·exp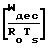 на основании которого определяется время размораживания. Время полного покрытия поверхности криопанелей мономолекулярным слоем задается выражением:
на основании которого определяется время размораживания. Время полного покрытия поверхности криопанелей мономолекулярным слоем задается выражением:
τпокр= 0,28·N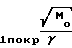 ·
· 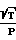 Равновесие между адсорбцией и десорбцией газов позволяет вычислить число молекул газа, осевших на поверхность в соответствии с зависимостью на 1 см2 поверхности:
Равновесие между адсорбцией и десорбцией газов позволяет вычислить число молекул газа, осевших на поверхность в соответствии с зависимостью на 1 см2 поверхности:
N1= 3,5·1022·τпр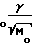
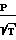 ·exp
·exp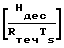 От количества осевших на поверхность молекул газа зависит степень заполнения поверхности θ, которая определяет величину коэффициента прилипания γ.
От количества осевших на поверхность молекул газа зависит степень заполнения поверхности θ, которая определяет величину коэффициента прилипания γ.
При учете абсорбции газов в твердых телах расчет потока от диффузии и проникания газа сквозь стенки ведется по закону Рауля, Генри и Сивертса в виде nr r ˙ Pu. При этом значение коэффициента растворимости вычисляется из уравнения
r ro·exp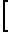 -
- 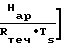 Диффузия газа в твердых телах по первому закону Фика дает значение потока
Диффузия газа в твердых телах по первому закону Фика дает значение потока
I1= -D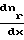 где D Do·exp
где D Do·exp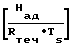 Проникание газа сквозь стенки сосудов может быть оценено коэффициентом проникания
Проникание газа сквозь стенки сосудов может быть оценено коэффициентом проникания
П Пo·exp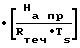 где По roDo. Поток газа с одного см2 в установившемся движении сквозь стенку определяется из уравнения.
где По roDo. Поток газа с одного см2 в установившемся движении сквозь стенку определяется из уравнения.
Ii= D·r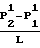 Общее количество газа за время τ, истекающего с единицы поверхности стенки при установившемся движении определяется по второму закону Фика Q1= 2n
Общее количество газа за время τ, истекающего с единицы поверхности стенки при установившемся движении определяется по второму закону Фика Q1= 2n
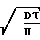 Для неустановившегося движения количество газа определяется как Q
Для неустановившегося движения количество газа определяется как Q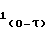 =
= 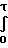 I1dr
I1dr 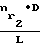 (τ-τo) τo=
(τ-τo) τo= 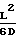
Это уравнение при Р ≅ Р2 и τ ≥ τo переходит к виду установившегося движения
Q1= Iiτ 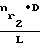 ·τ
·τ 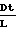 ·P
·P
При эксплуатации системы следует ожидать газовыделения и натекания в систему, при этом процесс газовыделения предполагает адсорбционное и диффузионное газовыделение, а также газопроницаемость. Удельная величина газовыделения может быть оценена по уравнению lgq A Bt. Натекание определяется: Qн Кв ˙ m ˙ Qтеч. Общая величина потока Qс при определенных условиях может быть сведена к минимуму.
Выше сообщалось, что к месту осаждения вещества присоединяется вакуумный насос или группа их. Наиболее целесообразным решением этой задачи с учетом развития науки и техники будет решение, включающее комбинацию последовательного соединения криогенного конденсационного насоса и, например, двухроторного вакуумного (насоса типа Рутса). Может быть выбрана и другая комбинация, однако принятое сочетание позволит в настоящий момент решить задачу создания необходимого режима при большом газоотделении (до 108 л/с). Быстрота действия криоконденсационного насоса выражается в молекулярном режиме уравнением:
S 3,64αA
3,64αA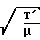 ·
·  1-
1- 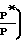 и в вязкостном режиме:
и в вязкостном режиме:
S αA
αA 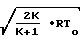
При значении (1- α) более критического 1-α 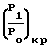
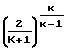 скорость потока ниже звуковой и быстроту откачки определяют по уравнению
скорость потока ниже звуковой и быстроту откачки определяют по уравнению
SD'' α A˙ W, а при скорости выше звуковой
SD''' 3,77 ˙ α X ˙ S'т
при X > 2, где X 
S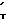 3,64·A
3,64·A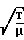
 1-
1- 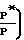
lgP* + BlgT+C+ Величина коэффициента криозахвата определяется расчетным путем для данного вида криопанелей методом Монте-Карло. Быстроту действия двухроторного насоса определяют:
+ BlgT+C+ Величина коэффициента криозахвата определяется расчетным путем для данного вида криопанелей методом Монте-Карло. Быстроту действия двухроторного насоса определяют:
S 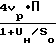 а расположение насосов должно быть на расстоянии, определяемым допустимым уровнем концентрации паров масла из уравнения:
а расположение насосов должно быть на расстоянии, определяемым допустимым уровнем концентрации паров масла из уравнения:
q qo·exp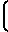 -
-  x
x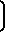
Уровень давления в системе зависит от ее объема и времени откачки
P Po·exp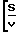 ·
· 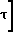 Время откачки находим по уравнению
Время откачки находим по уравнению
S [-2,3lg(Pт/760)]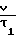 Sτ·v/τ1
Sτ·v/τ1
Наиболее ответственным моментом предлагаемого способа является решение задачи создания расчетного режима. Возможны три режима: вязкостный, переходный (вязкостно-молекулярный), молекулярный. Сообщается более дробное определение режимов. Учитывая, что отсутствует практика создания трубопроводов разреженного газа значительной протяженности (например, несколько тыс.км.) при большом диаметре (например 300-500 мм), в настоящей работе приводятся различные подходы решения данной задачи.
Вид течения разреженного газа определяется по числу Кнудсена
Кн 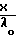 При
При  ≅ 1 имеет место молекулярный режим; для
≅ 1 имеет место молекулярный режим; для  ≥ 100 вязкостный и для 100 ≥ Кн ≥ 1 промежуточный. Основные уравнения, описывающие движение разреженного газа изложены в ряде работ. Наиболее известным является уравнение Паузейля
≥ 100 вязкостный и для 100 ≥ Кн ≥ 1 промежуточный. Основные уравнения, описывающие движение разреженного газа изложены в ряде работ. Наиболее известным является уравнение Паузейля
Q 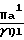 Pa(P2-P1)
Pa(P2-P1)
Уравнение Паузейля выведено с учетом ряда допущений: газ не сжимаем; течение полностью сформировано; турбулентное течение полностью отсутствует; скорость у стенки равна нулю; течение изотермическое.
Уравнение справедливо описывает движение в вязкостных условиях при скоростях, отвечающих значению числа Маха М ≅ 1/3. При этом средняя скорость по сечению равна
UfaQ/ π Q2P Уравнение Паузейля для случая сформированного течения при
l ≥ 0,304 aRe, где Re 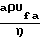 уточнено Лангхааром:
уточнено Лангхааром:
P2-P1= 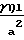 Ufa+1,14ρU
Ufa+1,14ρU
Q 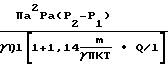 Для случая ламинарного течения при Re 1000 поток должен быть меньше, чем 3,72 ˙ 105 Q м тор. л/c для условий воздуха при t 25оС, где Q в см4, Q в м тор.л/с.
Для случая ламинарного течения при Re 1000 поток должен быть меньше, чем 3,72 ˙ 105 Q м тор. л/c для условий воздуха при t 25оС, где Q в см4, Q в м тор.л/с.
Возможны допущение 1: Q < 37Q2P млтор.л/с;
допущение 2: l ≥ 0,304 а Re и допущение 3: Q<3,72˙ 105 а м.тoр.л/с. Для воздуха при t 25оС, η 1,845 ˙ 10-4 пауз, если а и l выражается в сантиметрах, а давление в миллиметрах, выражение для пропускной способности имеет вид:
F 2,84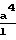 Pa мтор·л/с; F 2,84
Pa мтор·л/с; F 2,84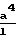
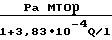 л/c Увеличение давления при поворотах и изменениях радиуса оценивается значением 1/2ρUfa2 или
л/c Увеличение давления при поворотах и изменениях радиуса оценивается значением 1/2ρUfa2 или 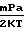 Ufa2. Режимы течения определяются: при
Ufa2. Режимы течения определяются: при
a Р мтор > 500 вязкостный;
a Р мтор < 5 молекулярный;
5 < Р мтор < 500 промежуточный;
a в см, Р в мторах.
В молекулярном режиме величина потока выражается соотношением Кнудсена:
Q 
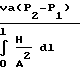 где va
где va 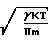
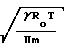 а проводимость F
а проводимость F 
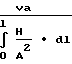 при этом для воздуха значение проводится для длинной трубы постоянного поперечного сечения равно
при этом для воздуха значение проводится для длинной трубы постоянного поперечного сечения равно
F 
 · va или F 19,40
· va или F 19,40
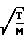 л/c Для цилиндрической трубы радиуса a
л/c Для цилиндрической трубы радиуса a
F 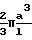 va
va
F 30,48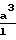
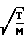 л/с
л/с
В промежуточном режиме течения учитывается скольжение газа на границе, при этом пропускная способность для трубы выражается.
F 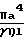 Pa
Pa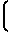 1+
1+ 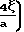 где ζ
где ζ 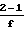 ·
· 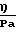 ·
· 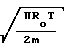 Наилучшую сходимость с опытом в стеклянных и медных трубах дает зависимость
Наилучшую сходимость с опытом в стеклянных и медных трубах дает зависимость
F F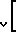 1+4
1+4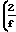 -1
-1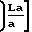 Значение f выражается:
Значение f выражается:
4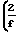 -1
-1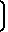 6,793
6,793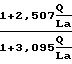 Значение A/Ft выражено по зависимости F F
Значение A/Ft выражено по зависимости F F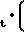 0,1472
0,1472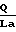 + Z
+ Z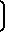 для значения:
для значения:
Z 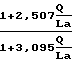 при условии постоянства динамической вязкости η 0,494. Для значения Q/La= 0,323 наблюдается минимум функции, а при
при условии постоянства динамической вязкости η 0,494. Для значения Q/La= 0,323 наблюдается минимум функции, а при 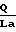 0
0 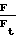 1 Величина газового потока в областях молекулярного течения пропорциональна (Р2 Р1), а в области вязкостного величине (Р22 -Р12).
1 Величина газового потока в областях молекулярного течения пропорциональна (Р2 Р1), а в области вязкостного величине (Р22 -Р12).
Движение газового потока в области молекулярного течения можно описать уравнением:
W πr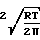 (na-nb)
(na-nb)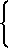 1-2
1-2 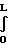 W(x)
W(x)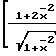 -2
-2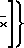 где выражение в фигурных скобках представляет собой коэффициент Клаузинга W.
где выражение в фигурных скобках представляет собой коэффициент Клаузинга W.
Для  ≥ 500 W
≥ 500 W 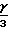
 а молекулярный и массовый расход выражается
а молекулярный и массовый расход выражается
W ωπr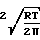 (na-nb)
(na-nb)
G Wπr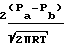 Течение в круглых трубах в широком диапазоне описывается зависимостью:
Течение в круглых трубах в широком диапазоне описывается зависимостью:
Q(δ) 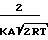
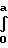 2πru(r)dr полученной из решения модельного уравнения. Экспериментальные исследования Донга, Бролея и Б. Т. Породнова удовлетворительно согласуются с теорией. Уравнение приведенного расхода имеет вид:
2πru(r)dr полученной из решения модельного уравнения. Экспериментальные исследования Донга, Бролея и Б. Т. Породнова удовлетворительно согласуются с теорией. Уравнение приведенного расхода имеет вид:
Q q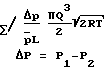 где
где 
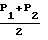 Δ P P1 P 2
Δ P P1 P 2
a радиус трубы, Т температура стенок, gΣ объемный расход газа через трубу.
Параметр разреженности δ 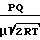
Приведенный расход Q может быть определен из зависимости Кнудсена:
Q 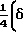 +8,52
+8,52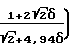 При этом режимы течения определяются показателем Кнудсена Кн ≅ 0,01- континуумное; К > 100 свободное молекулярное. Значения Кн задаются:
При этом режимы течения определяются показателем Кнудсена Кн ≅ 0,01- континуумное; К > 100 свободное молекулярное. Значения Кн задаются:
Kн= 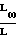
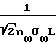 ;
;
σ πd2= 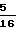
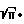 m
m 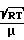 ;
;
Kн= 1,27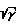 M/Re;
M/Re;
Re 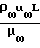 При гиперзвуковом обтекании:
При гиперзвуковом обтекании:
Kн= 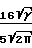
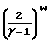
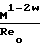
Reo= ρ∞u∞L/μo= 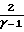
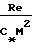
C*· 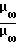
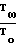
To= T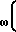 1+
1+ 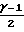 M
M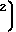 ≈
≈ 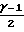 T∞M2 Область континуума может быть определена зависимостью L/l= Rej/M которая с учетом соотношения δ/L
T∞M2 Область континуума может быть определена зависимостью L/l= Rej/M которая с учетом соотношения δ/L 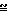 1/
1/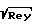 преобразуется к виду δ/L
преобразуется к виду δ/L 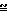
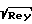 /M где δ толщина ламинарного пограничного слоя;
/M где δ толщина ламинарного пограничного слоя;
L характерный размер тела;
Rey ρ VL/ μ число Рейнольдса для тела;
М число Маха.
Газовая динамика континуума должна рассматривать задачи, в которых толщина пограничного слоя в 100 раз больше средней длины пробега, т.е.
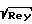 /M > 100 Соотношение L/l
/M > 100 Соотношение L/l 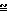 Rey/M свидетельствует, что концепция континуума не применима для очень больших значений числа Маха и для очень малых чисел Рейнольдса.
Rey/M свидетельствует, что концепция континуума не применима для очень больших значений числа Маха и для очень малых чисел Рейнольдса.
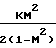
Характер изменения параметров потока зависит от того, какие значения принимает число Маха больше или меньше единицы, поскольку член (1 М2) присутствует во всех дифференциальных уравнениях в знаменателе: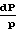
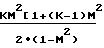 · 4f
· 4f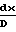
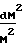 =
= 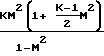 · 4f
· 4f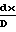
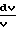
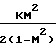 ·4f
·4f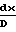
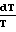

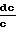
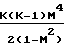 ·4f
·4f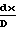
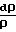
 ·4f
·4f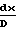
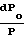
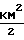 ·4f
·4f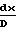
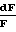
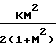 ·4f
·4f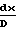
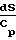
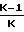 ·
· 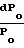
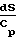
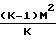 ·4f
·4f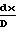
При учете сил трения изоэнтропное давление торможения и импульсная функция должны уменьшаться, а энтропия в адиабатических процессах не может уменьшаться, потому значение коэффициента трения f всегда больше нуля.
Характер изменения параметров потока определяется следующей таблицей.
Из сказанного следует, что число Маха стремится к единице. Плавный переход от дозвукового потока к сверхзвуковому потоку или наоборот невозможен. При данных начальных условиях потока на входе трубы ее максимально возможная длина, при которой начальные условия остаются неизменными и не появляются разрывы или скачки, определяется число Маха, которое должно быть точно равно 1.
Трение способствует увеличению скорости дозвукового потока и является причиной роста давления на сверхзвуковых скоростях.
В интегральной форме уравнения имеют нижеследующий вид и описывают движение газового потока практически при любых скоростях.
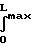 4f
4f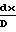
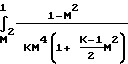 dm2 После интегрирования имеем
dm2 После интегрирования имеем
4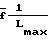
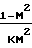 +
+ 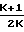 ln
ln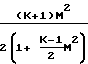 где f средний коэффициент трения, зависящий от длины и определяемый выражением:
где f средний коэффициент трения, зависящий от длины и определяемый выражением: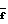
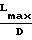
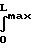 fdx Максимальная величина 4
fdx Максимальная величина 4 L/D дана для любого исходного значения числа Маха.
L/D дана для любого исходного значения числа Маха.
Длина трубы, которая необходима для перехода потока из состояния с числом Маха М1 в состояние с числом Маха М2 определяется как разность этих величин в начальном и исходном состояниях:
4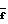

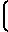 4
4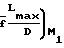 -
- 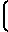 4
4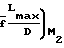 Из предыдущих уравнений получаем:
Из предыдущих уравнений получаем: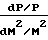
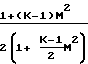
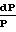
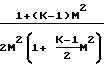 dM2 Обозначив давление в точке М 1 через Р*, проинтегрируем последнее уравнение в интервале сечений М М1, Р Р до М 1, Р Р* и получим:
dM2 Обозначив давление в точке М 1 через Р*, проинтегрируем последнее уравнение в интервале сечений М М1, Р Р до М 1, Р Р* и получим:
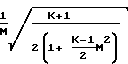
 M
M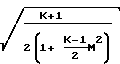

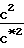
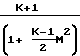



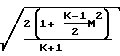


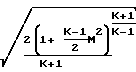

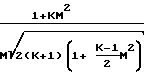
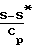 = lnM2
= lnM2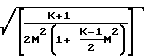
Величины Р*, Y* и т.д. являются параметрами потока для поперечного сечения трубы, в котором М 1.
Для определения параметра адиабатического потока в интервале сечений, в котором число Маха изменяется от М1 до М2, например:
P2/P1= 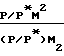
Наиболее важным моментом в решении задачи является выявление достаточно точного значения коэффициента трения. Для несжимаемого потока он выражается уравнением Кормана-Никурадзе.
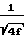 -0,8+2log10[Rey
-0,8+2log10[Rey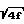 ] Rey число Рейнольдса для трубы, выраженное через диаметр. Коэффициент трения зависит от шероховатости. Эта зависимость установлена Моуди для дозвуковых потоков. Экспериментальные исследования, полученные Кинаном и Ньюманом, позволили установить, что значение очевидного коэффициента трения для сверхзвукового потока имеет значение в два раза меньше обычного, применяемого для несжимаемых потоков.
] Rey число Рейнольдса для трубы, выраженное через диаметр. Коэффициент трения зависит от шероховатости. Эта зависимость установлена Моуди для дозвуковых потоков. Экспериментальные исследования, полученные Кинаном и Ньюманом, позволили установить, что значение очевидного коэффициента трения для сверхзвукового потока имеет значение в два раза меньше обычного, применяемого для несжимаемых потоков.
В области разреженных газов достоверное значение коэффициента трения требует уточнения. В первом приближении он может быть оценен исходя из выражения для силы сопротивления, отнесенной к единице площади для течения Куэтта:
τw= 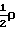 u
u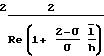 где U относительная скорость,
где U относительная скорость,
h расстояние между пластинами,
Re число Рейнольдса.
σ часть молекул, отраженных диффузно, средняя длина пробега молекулы. По аналогии для круглой трубы постоянного диаметра можно записать:
средняя длина пробега молекулы. По аналогии для круглой трубы постоянного диаметра можно записать:
f 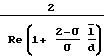 Запишем выражение для местной скорости потока u
Запишем выражение для местной скорости потока u 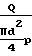 где Р ρ RT, тогда
где Р ρ RT, тогда
u 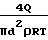 а f
а f 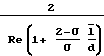
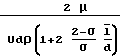

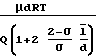
Местное значение f зависит от величины потока и с его ростом уменьшается. В континуумной среде местное значение f не может быть менее чем
f 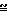

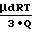
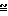

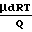 если не учитывать уменьшения динамической вязкости с возрастанием степени разрежения.
если не учитывать уменьшения динамической вязкости с возрастанием степени разрежения.
Вязкостный режим со скольжением описывается уравнением для массового расхода:
Qм= 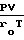
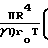 1+
1+ 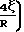 P
P
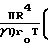 P+
P+ 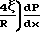 Уравнение можно представить в форме
Уравнение можно представить в форме
Qм= 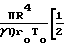 (P
(P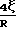 (P1-P2)
(P1-P2)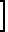 Коэффициент скольжения меняется как средний свободный пробег молекулы, т.е. обратно пропорционально давлению
Коэффициент скольжения меняется как средний свободный пробег молекулы, т.е. обратно пропорционально давлению
ζ ζ1/P; ζ1= ζP 2C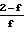 LP где 0,491 < С < 0,499,
LP где 0,491 < С < 0,499,
f коэффициент обмена количеством движения.
Расход газа в единицах записывается:
Q PV 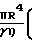 1+
1+ 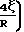 P
P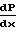 Для выявления ламинарности или турбулентности режима можно использовать уравнение для Re
Для выявления ламинарности или турбулентности режима можно использовать уравнение для Re
Re 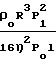 Уравнение получено при P2 0 и ρ
Уравнение получено при P2 0 и ρ 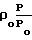 Последнее выражение справедливо только для изотермического течения.
Последнее выражение справедливо только для изотермического течения.
При Re ≅ 1000 имеет место ламинарный режим;
при Re > 1000 турбулентный.
Турбулентный режим в решении практических задач создания газовых потоков в магистральных трубопроводах. На основании экспериментальных исследований установлено, что ламинарный режим наблюдается при Re < 1200, а турбулентный при Re > 2200.
Основное уравнение для молекулярного режима имеет вид
Qм= 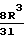
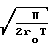 (P1-P2) При L < R справедливо:
(P1-P2) При L < R справедливо:
Qм= 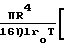 1+
1+ 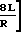 (P
(P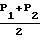 , т.к. давление по длине трубопровода не изменяется по закону прямой, и указанное упрощение может оказаться несправедливым.
, т.к. давление по длине трубопровода не изменяется по закону прямой, и указанное упрощение может оказаться несправедливым.
Для переходного режима Кнудсеном предложены выражения
F α1Pм+α2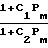 см3/с где Рт среднее давление в барах
см3/с где Рт среднее давление в барах
α1= 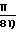

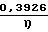
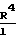 см3/с·бар
см3/с·бар
α2= 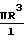 Ua 3,0476
Ua 3,0476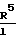
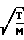 см3/с
см3/с
C1= 2R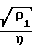
C2= 2,47R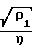 Функция проводимости выражается:
Функция проводимости выражается:
F 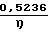 ·
· 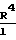 + 3,048·104·Z
+ 3,048·104·Z
М молекулярная масса:
Т температура газа.
Z 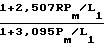
L1 средний свободный пробег молекул газа при рассматриваемой температуре,
Рт среднее давление в барах. Исходя из этих формул, можно получить уравнения, определяющие приведенный расход (РV), массовый расход и объем при давлении Р и среднюю скорость U
QPV= F(P1-P2) 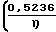 + 3,048·104·Z
+ 3,048·104·Z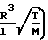 (P1-P2)
(P1-P2)
Qм= 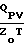
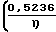
 + 3,048·104·Z
+ 3,048·104·Z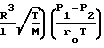
V 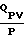
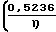
 + 3,048·104·Z
+ 3,048·104·Z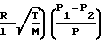
U 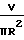
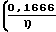
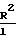 + 0,9707·104·Z
+ 0,9707·104·Z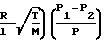 Среднее значение давления выражается:
Среднее значение давления выражается:
Pм= 
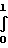 Pdx
Pdx
Pм= 
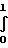
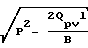 dl,
dl,
где где B 
Pм= 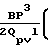 1-
1- 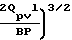 Окончательно среднее давление получаем
Окончательно среднее давление получаем
Pм=  P′-
P′- 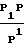 где P1=
где P1= 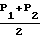 Наложение режимов можно выполнить с помощью формулы
Наложение режимов можно выполнить с помощью формулы
σ l-2/Kn -0,2) где σ часть молекул, отвечающих закону молекулярного режима
Fn (1 σ )Fc + σ Fм, где Fc проводимость в режиме скольжения;
Fм проводимость в молекулярном режиме. При f ≠ 1 проводимость определяется:
F
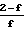 Fn Основные уравнения для молекулярного режима могут быть записаны
Fn Основные уравнения для молекулярного режима могут быть записаны
Qм= 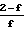
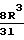
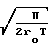 (P1-P2)
(P1-P2)
Qpv= 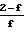
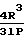
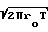 (P1-P2)
(P1-P2)
V 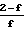

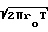 (P2-P1)
(P2-P1)
U 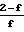
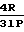
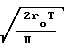 (P1-P2) Средняя скорость на выходе
(P1-P2) Средняя скорость на выходе
U2= 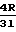
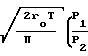 -1
-1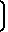 При температуре воздуха 17оС имеем
При температуре воздуха 17оС имеем
U2= 3,0723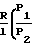 -1
-1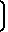 см/с см/с. Проводимость
см/с см/с. Проводимость
F 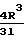
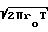 или с молекулярной массой М
или с молекулярной массой М
F 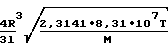
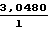
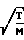 R3 см3/с при написании уравнений предполагалось, что труба имеет бесконечную длину, стенки полностью рассеивают молекулы, газ находится в равновесии и подчиняется закону Максвелла.
R3 см3/с при написании уравнений предполагалось, что труба имеет бесконечную длину, стенки полностью рассеивают молекулы, газ находится в равновесии и подчиняется закону Максвелла.
Характер режима и выбор уравнений зависит от числа Кнудсена. При Кн≥ 10 имеет место молекулярный режим,
0,25 ≅ Кн ≅ 10 переходный режим,
10-3 < Кн < 0,25 режим со скольжением,
Кн < 10-3 режим классической аэродинамики.
Для описания движения газа в трубах используется число Кнудсена, которое выражается как отношение средней длины свободного пробега молекулы к радиусу трубы Кн L/R. Для характеристики движения тел в разреженных газах число Кнудсена выражается как отношение L к характеристическому размеру тела или толщине пограничного слоя.
Коэффициент вязкости в молекулярном режиме изменяется. Вязкость газа может быть выражена формулой:
Z 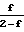
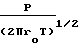 Исследования показывают, что для адиабатических условий существует предельная скорость движения разреженного газа:
Исследования показывают, что для адиабатических условий существует предельная скорость движения разреженного газа:
U2= 2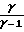 roT
roT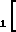 1-
1-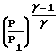 Предельное значение выражается
Предельное значение выражается
U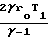 В функции средней квадратичной скорости молекул
В функции средней квадратичной скорости молекул 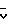 :
:
U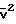 = 2γ/3(γ-1) В случае двухатомного газа γ 7/5
= 2γ/3(γ-1) В случае двухатомного газа γ 7/5
U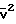 = 7/3 Для одноатомного газа γ 5/3
= 7/3 Для одноатомного газа γ 5/3
U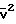 =
=  Число Маха можно вычислить
Число Маха можно вычислить
M2= 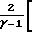 1-
1-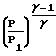 Вместе с тем опыт показывает, что в коротких трубах можно достичь числа Маха 5, 6 и более. Эта область супераэродинамики характеризуется числом Кнудсена, когда средний свободный пробег становится больше размеров движущегося тела.
Вместе с тем опыт показывает, что в коротких трубах можно достичь числа Маха 5, 6 и более. Эта область супераэродинамики характеризуется числом Кнудсена, когда средний свободный пробег становится больше размеров движущегося тела.
В этой области изменения величины отношений числа молекул, сталкивающихся с передней и задней кромкой плоскости, к числу молекул, ударяющихся о пластину с тех же сторон, но когда неподвижная пластина находится в покоящемся газе, характеризуется значениями:
χ′ e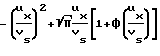
χ″ e Изменения зависят от значения нормальной скорости пластины или от отношения этой составляющей и наиболее вероятной скорости молекул газа в предложении максвеллового распределения.
Изменения зависят от значения нормальной скорости пластины или от отношения этой составляющей и наиболее вероятной скорости молекул газа в предложении максвеллового распределения.
Известны значения для κ' и κ''. При 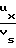 ≥1,6 число молекул, ударяющихся в заднюю кромку равно 1/100 т.е. примерно равно нулю. При этом
≥1,6 число молекул, ударяющихся в заднюю кромку равно 1/100 т.е. примерно равно нулю. При этом 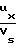
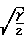 M где М число Маха.
M где М число Маха.
При движении твердого тела в разреженном газе при очень малых числах Маха коэффициент трения для сферы может быть выражен зависимостью
Cf= 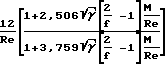 Сопротивление сферы Бассетом записано в форме:
Сопротивление сферы Бассетом записано в форме:
Cf· 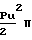 R2= F при этом
R2= F при этом
Cf= 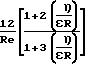 где L 1,25
где L 1,25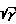 · η/ρc
· η/ρc
С скорость звука при данной температуре.
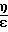 0,998
0,998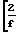 -1
-1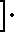 L
L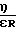 0,998
0,998 -1
-1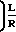 1,253
1,253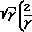 -1
-1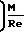
Для дозвуковых и сверхзвуковых скоростей Кейном получена эмпирическая зависимость для сферы:
CD= 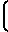 0,97+
0,97+ 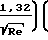 1+
1+ 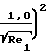 где Re1 значение числа Рейнольдса за ударной волной. Выражение для СDполучено для чисел Рейнольдса от 15 до 768.
где Re1 значение числа Рейнольдса за ударной волной. Выражение для СDполучено для чисел Рейнольдса от 15 до 768.
Характерным явлением в разреженных газах является скачек скорости и температуры у твердой границы. Температурный скачек уточнен П. Валандером:
ΔT 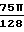
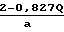
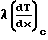
Q 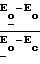 где Q коэффициент аккомодации энергии.
где Q коэффициент аккомодации энергии.
Значение ΔТ выражается:
ΔT To-Tw= κт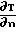
κт= 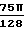 ·
· 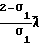 где σ1 коэффициент аккомодации тангенциального импульса количества движения
где σ1 коэффициент аккомодации тангенциального импульса количества движения
κт= 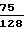 ·
· 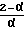
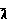 где α коэффициент аккомодации энергии. Для многоатомного газа
где α коэффициент аккомодации энергии. Для многоатомного газа
κт= 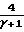 ·
· 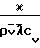 ·
· 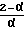
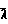 Скорость скольжения вдоль поверхности можно найти из соотношения
Скорость скольжения вдоль поверхности можно найти из соотношения
us= κм· 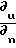
κv= 2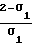 ·
· 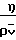
κv= 2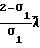 где σ1 коэффициент аккомодации тангенциального импульса движения.
где σ1 коэффициент аккомодации тангенциального импульса движения.
Для условий справедливости уравнений Навье-Стокса значение температурного скачка и скорости:
ΔT T°-Tw= 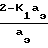 ·
· 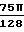 ·l
·l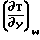
u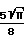 ·l
·l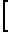 K
K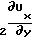 + K
+ K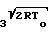
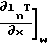 где y координата, описываемая от стенки по нормали,
где y координата, описываемая от стенки по нормали,
Тw температура поверхности тела,
То и ux граничные значения температуры и скорости газа при
Ki (Ki 0,827; K2 1,012; K3 0,42)
l средняя длина пробега молекулы,
Qэ термический коэффициент аккомодации (не слишком мал по сравнению с единицей).
Наиболее важным этапом в решении задачи переноса массы в разряженных газах является описание течения смеси газа с частицами. Достаточно обнадеживающие результаты работ пока не найдены.
Описание течения смеси газа с частицами дается с учетом ряда допущений
ρg·ugA 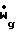
ρpiupiA 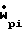
Wgdug+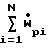 dupi+AdPg= 0
dupi+AdPg= 0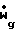 [Cpg(Tg-Tgo)+
[Cpg(Tg-Tgo)+  u
u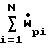 [Cpp(Tpi-Tgo)+
[Cpp(Tpi-Tgo)+  u
u
Pg ρgRTg
upi(dupi/dx)  (Mgfpir*/mpr
(Mgfpir*/mpr
Upi(dTpi/dx)= -3(Mgggir*/mprpi2) (Cpg/PrCpp)(Tpi-Tg) Низкочастотные бесконечно малые возмущения распространяются с равновесной скоростью звука: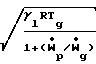 где γl=
где γl= 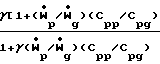 Так как γе < γ, то равновесная скорость звука в смеси газа с частицами меньше неравновесной или замороженной скорости звука в смеси.
Так как γе < γ, то равновесная скорость звука в смеси газа с частицами меньше неравновесной или замороженной скорости звука в смеси.
Для многофазных систем число Маха газовой фазы в горле равно:
Mg2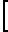 1+
1+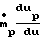 +
+ 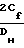 u
u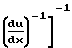
Число Маха газа в горле для многофазных систем, вычисленное по скорости звука в газе, равно 0,8.
Решение уравнений для течения смеси газа с частицами в условиях справедливости закона Стокса и частиц одинакового размера имеет вид:
A2/A*2 (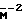 )
)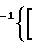 2(
2(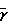 +1)
+1)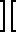 1+
1+  (
(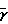 -1)
-1)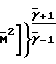
Pgo/Pg= 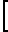 1+
1+  (
(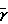 -1)
-1)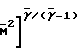
ρgo/ρg= 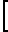 1+
1+  (
(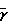 -1)
-1)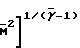
Τgo/Τg= 1+  (
(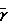 -1)
-1)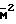
ug/ugmax= 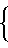 [(
[(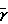 -1)
-1)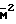 ]/[2+(
]/[2+(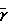 -1)
-1) ]
]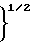
ug= 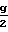 (μg·r*/mpr
(μg·r*/mpr
up= Kug, ρp= (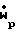 /
/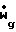 )(ρgK)
)(ρgK)
Tp=LTg+(1-L)Tgo
L 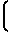 1+3Pr
1+3Pr ·
· 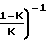
B 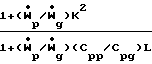
C 1+(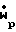 )/(
)/(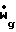 ){K[(1-K)γ+K]+(γ-1)(Cpp/Cpg)BL}
){K[(1-K)γ+K]+(γ-1)(Cpp/Cpg)BL} C1/2M
C1/2M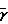 1+(γ-1)(B/C)
1+(γ-1)(B/C)
ugmax Градиент осевой скорости есть величина постоянная в соплах с постоянным запаздыванием. Данный вывод, как показали исследования Гильберта, является общим. Карье показал, что в случае движения, когда не соблюдается закон Стокса, имеет место зависимость СD˙Re/Nu
Градиент осевой скорости есть величина постоянная в соплах с постоянным запаздыванием. Данный вывод, как показали исследования Гильберта, является общим. Карье показал, что в случае движения, когда не соблюдается закон Стокса, имеет место зависимость СD˙Re/Nu  12,
12,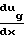
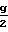 (μgfr*/mpr
(μgfr*/mpr
Исследования влияния факторов разреженности, сжимаемости и ускорения свободного потока на коэффициент сопротивления и теплоотдачи показывают, что только разреженность оказывает влияние. Учет осуществляется введением поправки:
CD= C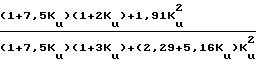
Nu=  где CD, Nu коэффициенты сопротивления и теплоотдачи шара при отсутствии разреженности.
где CD, Nu коэффициенты сопротивления и теплоотдачи шара при отсутствии разреженности.
Оценить перенос массы в разреженных газах невозможно без установления единого критерия переноса. Исследования транспортирования материалов в пылепроводах позволили установить, что при критических скоростях газа в трубопроводе не происходит осаждения вещества и обеспечивается перенос массы. Аналитическая обработка экспериментальных данных позволила установить общую функциональную зависимость:
lgReкр= f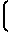 lg
lg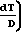 которая аппроксимируется уравнением для частиц первой группы 10 мм ≥ dТ≥ 0,75 мм
которая аппроксимируется уравнением для частиц первой группы 10 мм ≥ dТ≥ 0,75 мм
Reкр (280 D 5) ˙ 104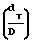 0,4, для частиц второй группы 0,375 мм ≥ dТ ≥ 0,10 мм
0,4, для частиц второй группы 0,375 мм ≥ dТ ≥ 0,10 мм
Reкр 53 ˙ 104 ˙ D (dT/D)0,123 для частиц третьей группы 0,025 мм ≥ dT ≥ 0,009 мм
Reкр (16 D + 0,16) ˙ 104 ˙ (dТ/D)-0,173 чему соответствуют критические скорости
Vкр ≥ 0,75 ˙ (56 -1/D)(dТ/D)0,4,
Vкр ≥ 8 (dТ/D)0,123,
Vкр ≥ 0,24 (100 + 1/D)(dТ/D)-0,173.
Распределение скорости в трубах в условиях нормального или избыточного давлений подчиняется закону одной седьмой
Vу/Vср= (1+1,443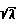 )(2y/D)1/7
)(2y/D)1/7
Значение приданной скорости набегающего потока выражается:
Vн= Vкр(1+1,443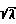 )(dT/D)1/7 Уравнения относятся к пылевым смесям с плотностью 2500 кг/м3. Для других плотностей вводится поправочный коэффициент
)(dT/D)1/7 Уравнения относятся к пылевым смесям с плотностью 2500 кг/м3. Для других плотностей вводится поправочный коэффициент 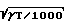 Значение λ принимается с учетом уравнения Л. Д. Альтшулера при относительной шероховатости
Значение λ принимается с учетом уравнения Л. Д. Альтшулера при относительной шероховатости  4 ˙ 10-4 1,6 ˙ 10-4 и скорости воздуха V 17- 50 м/с; Re 0,57 ˙105 41,7 ˙ 105
4 ˙ 10-4 1,6 ˙ 10-4 и скорости воздуха V 17- 50 м/с; Re 0,57 ˙105 41,7 ˙ 105
λ 0,1/1,46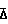 +100(Re)0,25 или по формуле Г. А. Мурина для гидравлически гладких труб:
+100(Re)0,25 или по формуле Г. А. Мурина для гидравлически гладких труб:
λ=1,01/(gRe)2,5 для гидравлически шероховатых:
λ 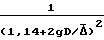 Граничные числа Рейнольдса, Re
Граничные числа Рейнольдса, Re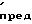 = 23/
= 23/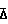 , при которых начинает влиять шероховатость, и Re
, при которых начинает влиять шероховатость, и Re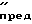 = 560/
= 560/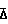 при которых начинает действовать квадратичный закон сопротивления. Среднее значение λ 0,018-0,0020.
при которых начинает действовать квадратичный закон сопротивления. Среднее значение λ 0,018-0,0020.
При определении критического параметра переноса массы важно помнить, что закон Стокса F 3πμdVc справедлив при малых значениях числа Рейнольдса для частицы Rea ≅ 1. Для больших чисел Рейнольдса перенос массы описывается уравнениями
F 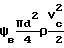 где при Re < 5 Ψ
где при Re < 5 Ψ 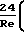 1+
1+ 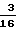 Re
Re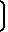 а при 3 < Re < 400 по формуле Колячко Ψ
а при 3 < Re < 400 по формуле Колячко Ψ 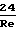 + 4
+ 4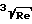 Для больших значений числа Re по уравнению Ньютона F 0,055πμвd2Vc2, что соответствует ϑ 0,41.
Для больших значений числа Re по уравнению Ньютона F 0,055πμвd2Vc2, что соответствует ϑ 0,41.
Перечисленные уравнения справедливы в условиях нормального или избыточного давления и малопригодны или вообще не справедливы для разреженных газов. Тем не менее параметр динамического давления ρ V2/2 является определяющим при назначении критического режима. C учетом исследований за критический параметр в разреженных газах следует принять значения динамического давления, эквивалентного минимальному по условиям переноса в пограничном слое, т.е. ρвUн2/2, где ρв плотность воздуха в пограничном слое; Vн скорость воздуха в набегающем потоке.
Вероятность столкновения молекул с частицами в разреженной среде учитывается введением параметра η
η S-2erfS+2S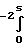 x erf xdx, где S uo/
x erf xdx, где S uo/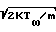 Таким образом, в первом приближении условие обеспечения переноса массы должно быть записано в форме η·ρW·
Таким образом, в первом приближении условие обеспечения переноса массы должно быть записано в форме η·ρW·  ≥
≥ 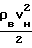 (1). В разреженных газах условие (1) является необходимым, но не достаточным и связано с несоблюдением закона Стокса в разреженных газах.
(1). В разреженных газах условие (1) является необходимым, но не достаточным и связано с несоблюдением закона Стокса в разреженных газах.
Исследование минимальной скорости переноса показывает, что оно зависит как от величины скорости трения Uw* так и от конечной скорости осаждения Ut и характеризуется числом Рейнольдса в форме
Rea const 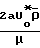 ·
·  Значения Rea определяют области режима течения: Rea < 1 стоксов режим; 1 < Rea < 500 переходная область; Rea > 500 ньютоновский режим течения.
Значения Rea определяют области режима течения: Rea < 1 стоксов режим; 1 < Rea < 500 переходная область; Rea > 500 ньютоновский режим течения.
Установлено, что течение обеспечивается, если соблюдается условие для бесконечно малой концентрации 0,204
0,204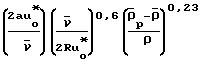 где
где 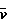
 /
/ а для любой концентрации
а для любой концентрации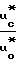 1+2,8
1+2,8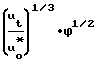 где значение скорости трения Uw* определяется
где значение скорости трения Uw* определяется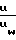 5lgRe-3,90
5lgRe-3,90
Значение скорости трения определяется выражением u*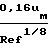
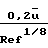 где
где  средняя скорость течения газа. Для характеристики ламинарного слоя используется зависимость отношения подъемной силы к силе сопротивления в виде
средняя скорость течения газа. Для характеристики ламинарного слоя используется зависимость отношения подъемной силы к силе сопротивления в виде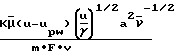 =
= 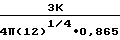
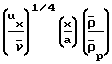 для значений Fx/U << 1. Для развитого течения зависимость записывается в форме
для значений Fx/U << 1. Для развитого течения зависимость записывается в форме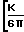 (0,865)·21/4·3
(0,865)·21/4·3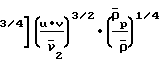 при x
при x  Отношение
Отношение  Nм= (x*)-1=
Nм= (x*)-1= 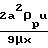 называется критерием межфазного обмена количеством движения. Число идентично числу Рейнольдса газовой фазы
называется критерием межфазного обмена количеством движения. Число идентично числу Рейнольдса газовой фазы
Rex  Приведенный выше критерий переноса массы выражает слабое влияние разреженной среды и не может в полной мере служить мерилом переноса массы. Более полное и точное выражение могло быть получено при характеристике режима отношением суммы подъемной силы, силы сопротивления при оседании смеси, градиента давления по высоте к силе сопротивления при переносе массы. Вопрос требует изучения.
Приведенный выше критерий переноса массы выражает слабое влияние разреженной среды и не может в полной мере служить мерилом переноса массы. Более полное и точное выражение могло быть получено при характеристике режима отношением суммы подъемной силы, силы сопротивления при оседании смеси, градиента давления по высоте к силе сопротивления при переносе массы. Вопрос требует изучения.
При переносе массы вследствие существования трибоэлектрического эффекта наводится статическое электричество на твердых сыпучих телах, которые вызывают поляризацию проводящих стен трубопровода.
Наличие поляризационного заряда проводящей стенки и пространственного заряда множества частиц проявляется в существовании дрейфовой скорости массы на стенки трубопровода и изменении распределения концентрации, изменений поперечной скорости V, напряженности Ey. Наличие электрического заряда вносит корректив в критерий переноса массы.
Возможно решение задачи со следующими данными: двумерное движение в электрическом поле (i 1, 2); движение частиц не оказывает существенного влияния на движение непрерывной фазы (считается, что концентрация частиц не должна составлять более 0,25 кг/м3; все частицы имеют один размер (S 1). При этих допущениях значения основных параметров определяется уравнением: для дрейфовой скорости
V -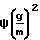
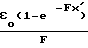 для функции тока
для функции тока
-Ψ 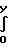 ρdy ρpob
ρdy ρpob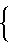 y
y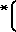 1+x
1+x +
+ 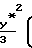 1+x
1+x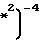 +
+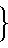 для распределения концентрации
для распределения концентрации
ρ* ( 1 + x*2 ) -1 + y*2 ( 1 + x*2 ) -4 +. распределение дрейфовой скорости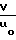
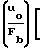 1-e
1-e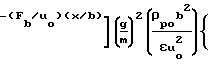 y
y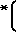 1+x
1+x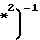 +
+
+ y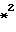 /3
/3 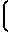 1+x
1+x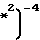 +
+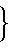 где ρ*
где ρ*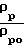
x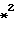 =
= 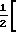 1+
1+ 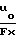 ·e
·e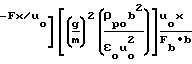
y*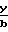
Значение 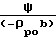 ≥ указывает на наличие осажденного слоя. Массовая скорость столкновений частиц с единицей поверхности дна задается выражением [ρbV/w при y* 1
≥ указывает на наличие осажденного слоя. Массовая скорость столкновений частиц с единицей поверхности дна задается выражением [ρbV/w при y* 1
[ρpV] w= 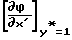 =
= 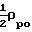 uoRe
uoRe 1-
1-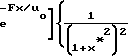 -
-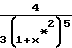 +
+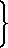 Распределение дрейфовой скорости V/Uo предлагается истолковывать с учетом понятий электрического числа Рейнольдса
Распределение дрейфовой скорости V/Uo предлагается истолковывать с учетом понятий электрического числа Рейнольдса
Re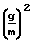
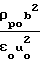 и числа электровязкости Ev:
и числа электровязкости Ev:
Ev= 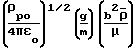
При оценке роли электрических сил при движении пограничного слоя делается допущение о том, что электрические силы достаточно малы по сравнению с гидродинамическими, т.е. их можно принять за возмущения.
Изменения в толщине пограничного слоя записываются в форме:
δ pν δ1p(o) + β1 δp1(1) + β1 δp1(1') Возмущение первого порядка выглядит:
δp1= 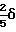 x*+
x*+ 
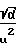
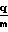
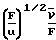 x
x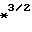 -
- 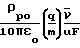 x
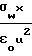
x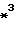 Влияние электрического поля пластины незначительно, если:
Влияние электрического поля пластины незначительно, если:
Re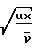 ≫
≫ 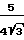
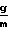
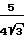 Reewx Электрический эффект будет несущественен, если:
Reewx Электрический эффект будет несущественен, если:
Re
Evwx= 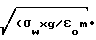 (x/
(x/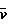 )
)
Evpw= 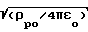 (g/m)(x2/
(g/m)(x2/ ) Уравнения принимают вид:
) Уравнения принимают вид:
Re
Re5/2 ≫ E или в общем виде Rex≫ Evx
или в общем виде Rex≫ Evx
Таким образом, изложенное позволяет установить сущность предлагаемого способа.
Экономическая эффективность системы транспорта материалов, а также капсул предложенным способом в сравнении с другими видами транспорта определяется преимуществами способа, к которым следует отнести:
исключение трудоемких погрузочно-разгрузочных работ и непрерывность транспортно-технологического процесса;
возможность прокладки трубопровода по кратчайшему расстоянию между двумя пунктами;
малые площади, занимаемые транспортными коммуникациями;
возможность создания полностью автоматизированных и дистанционно управляемых систем транспорта.
Перечисленные достоинства являются общими для различных систем трубопроводного транспорта. Применительно к предлагаемому способу надо отметить другие, не менее важные преимущества:
отсутствие пылеобразования и потерь транспортируемого материала, воздействуя на окружающую среду (Достоинство также присуще способу транспортирования в жидких средах);
высокая скорость перемещения материала. Величина скорости газа может принимать значения, равные нескольким числам Маха. Следует иметь в виду отставание скорости материала от скорости газа;
снижение энергетических затрат, которые в сравнении с методом транспорта в жидких средах будет уменьшаться в зависимости от отношения плотности смеси в жидкой среде к плотности смеси и газообразной среде. Снижение энергоемкости будет наблюдаться также в связи с ростом дальности плеча транспортировки, что вызвано понижением коэффициента трения газа с ростом потока и падением давления, а также незначительным влиянием сухого трения материала или полным его отсутствием. Последнее особенно существенно в сравнении с транспортировкой материала с использованием жидких сред и газов с избыточным давлением;
использование разреженных газов и объемных вакуумных насосов позволит уменьшить энергопотребление насосной установки при переходе ее на режим работы при пониженных давлениях, что исключается при использовании других транспортных сред;
исключаются затраты по обезвоживанию материала, расширяется номенклатура транспортируемых материалов. Например, при организации транспорта угля он будет размалываться на месте добычи и в дальнейшем использоваться в пылеобразном состоянии, что значительно эффективнее с точки зрения механизации процессов и улучшению его сгорания;
снижение единовременных затрат на прокладку трубопровода, т.к. расчетное давление транспортирующей среды в нем значительно ниже, а абразивный износ стенок меньше при большей пропускной способности по материалу вследствие значительных скоростей потока;
снижение потребления сжатого газа для транспорта материала; при этом его величина не зависит от дальности плеча транспортирования, как это имеет место в случае транспорта газом в избыточном давлении;
возможность разделить вещество от газа практически на любом наперед заданном уровне, к тому же без использования фильтров, особенно важно в случае применения ядовитых веществ;
практически не ограниченная дальность транспортирования материала, что особенно важно для развития районов Дальнего Востока и Сибири;
не исключается использование в других областях техники.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ исследования обтекания сферических тел | 1960 |
|
SU140272A1 |
| Способ смешения сверхзвуковых газовых потоков в разреженной среде | 1983 |
|
SU1109185A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ФИЗИЧЕСКИХ СВОЙСТВ ПРИРОДНОГО ГАЗА И УСТРОЙСТВО ДЛЯ ЕГО АВТОМАТИЧЕСКОГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2269113C1 |
| УСТРОЙСТВО ДЛЯ РАСПЫЛЕНИЯ ЖИДКОСТИ | 1994 |
|
RU2083247C1 |
| ПАРОГЕНЕРАТОР ДВУХКОНТУРНОЙ АТОМНОЙ ЭЛЕКТРОСТАНЦИИ | 1995 |
|
RU2118854C1 |
| СПОСОБ ПОЛУЧЕНИЯ ГИПЕРЗВУКОВОГО ПОТОКА | 1996 |
|
RU2101691C1 |
| СТРУЙНЫЙ РАСХОДОМЕР И СПОСОБ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2421690C2 |
| СПОСОБ ИЗМЕРЕНИЯ МАССОВОГО РАСХОДА И МАССОВОГО ПАРОСОДЕРЖАНИЯ ПАРОЖИДКОСТНОГО ПОТОКА | 1998 |
|
RU2164341C2 |
| Способ разработки нефтяной залежи водогазовым воздействием | 2021 |
|
RU2762641C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАСХОДНОЙ ХАРАКТЕРИСТИКИ ГИДРАВЛИЧЕСКОГО ТРАКТА ДЛЯ ОБЛАСТИ ПЕРЕХОДА ОТ ТУРБУЛЕНТНОГО К ЛАМИНАРНОМУ РЕЖИМУ ИСТЕЧЕНИЯ | 2019 |
|
RU2709034C1 |

Использование: в технике транспортирования газом сыпучих веществ, аэрозолей, а также сформированных капсул. Сущность: в способе транспортирования сыпучих веществ, аэрозолей и капсул заключается во вводе газа и перемещаемого материала в транспортный трубопровод, в котором предварительно создано разрежение. Газ вводят в трубопровод со скоростью не ниже местной скорости звука, затем вводят транспортируемый материал. Уровень давления по длине трубопровода поддерживают постоянным. 1 табл.
СПОСОБ ТРАНСПОРТИРОВАНИЯ СЫПУЧИХ ВЕЩЕСТВ, АЭРОЗОЛЕЙ И КАПСУЛ, заключающийся в виде газа и перемещаемого материала в транспортный трубопровод, в котором предварительно создано разрежение, отличающийся тем, что газ вводят в трубопровод со скоростью не ниже местной скорости звука, затем вводят транспортируемый материал, а уровень давления по длине трубопровода поддерживают постоянным.
| Всасывающе-нагнетательная установка для пневмотранспортирования сыпучих материалов | 1982 |
|
SU1055714A1 |
| Разборное приспособление для накатки на рельсы сошедших с них колес подвижного состава | 1920 |
|
SU65A1 |
Авторы
Даты
1995-06-19—Публикация
1986-12-11—Подача