Предлагаемое изобретение относится к области измерений физических величин, в частности к теплофизическим измерениям свойств материалов, которые эксплуатируют в области температур, где свойства имеют ярко выраженную зависимость от температуры, таких как графит, карбиды и другие. Изобретение может найти применение при определении свойств электропроводных материалов, которые применяются в настоящее время или будут использоваться в дальнейшем в общей энергетике, авиационно-космической, химической и других отраслях техники.
Известен способ определения коэффициента теплопроводности λ (В.Э.Пелецкий, Д.Л.Тимрот, В.Ю.Воскресенский. Высокотемпературные исследования тепло- и электропроводности твердых тел, Москва: Энергия, 1971 г., стр.89), включающий нагрев постоянным током одного толстостенного образца в виде цилиндрической трубки с радиусами R и r, измерение на изотермическом участке длиной L силы тока I, падения напряжения U, истинной температуры внутренней поверхности полого цилиндрического образца Т и определение коэффициента теплопроводности. В качестве первого приближения для определения среднего в интервале температур T2-Т1 коэффициента λ использовалось выражение, отвечающее решению задачи теплопроводности через цилиндрическую стенку с внутренними источниками теплоты qv=const и при постоянных свойствах материала:
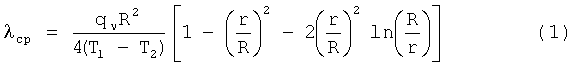
где qv=4·I·U/π(R2-r2)·L.
Во втором приближении для определения окончательных значений коэффициента теплопроводности и температуры отнесения использовались линейные зависимости коэффициентов теплопроводности и удельного электрического сопротивления от температуры, полученные в первом приближении, а температурное распределение по радиусу цилиндрического образца находилось по уравнению:
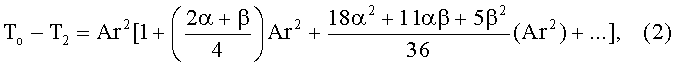
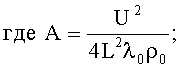
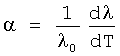 ;
; 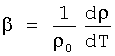 ,
,
теплопроводность λ0 и электропроводность ρ0 отнесены к температуре на оси цилиндрического стержня. Недостатком данного способа является то, что для второго приближения используется аналитическое выражение (2), которое получено в предположении, что r=0, что эквивалентно сплошному цилиндру, тогда как эксперимент проводится на полом цилиндрическом образце. Соответствующие ряды уравнения (2) для полых цилиндрических образцов с увеличением внутреннего радиуса сходятся все медленнее, что снижает точность способа, так как усложняет задачу отыскания локальных значений исследуемых параметров. Применение указанного аналитического решения диктует необходимость использования в эксперименте толстостенных образцов, что приводит к большим перепадам температуры по радиусу образца, что также понижает точность определения локальных значений коэффициента теплопроводности. Следующим недостатком способа является ограничение на использование только линейной зависимости свойств λ и ρ от температуры, что дополнительно понижает точность определения коэффициента теплопроводности.
Наиболее близким к предлагаемому изобретению является способ определения температурной зависимости коэффициента теплопроводности твердых, изотропных электропроводящих материалов (В.А.Петров. Излучательная способность высокотемпературных материалов. Москва: Наука, 1969 г., стр.28, прототип), включающий нагрев постоянным током двух полых цилиндрических образцов с разной толщиной стенки, измерение на изотермических участках длиной L силы тока I, падения напряжения U, истинной температуры внутренней поверхности Т, пост роение зависимостей q1=U·I/π·2R1·L=f(T1), q2=U·I/π·2R2·L=f(T2), и при одинаковых значениях плотности теплового потока на единицу поверхности q1=q2=qs определяют соответствующие температуры внутренней поверхности двух полых цилиндрических образцов Т1 и T2 и рассчитывают значения коэффициента теплопроводности по формуле
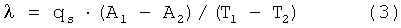
где A1 и А2 - коэффициенты, зависящие только от радиусов R и r.
Данное уравнение получено на основе совместного решения для двух полых цилиндров с различной толщиной стенки стационарного линейного дифференциального уравнения теплопроводности с постоянно действующими внутренними источниками теплоты qν=const. Предполагается, что теплота отводится только через наружную поверхность трубы, а на внутренней поверхности q=λ(dT/dr)=0, то есть рассматриваются граничные условия второго рода. При этом предполагается, что свойства исследуемого материала не зависят от температуры. После нахождения температуры отнесения данный способ позволяет определить и температурную зависимость коэффициента теплопроводности λ=f(Tотн).
Недостатком способа является низкая точность, так как в дифференциальном уравнении теплопроводности не учитывается зависимость свойств исследуемого материала от температуры.
Предлагаемый способ решает техническую задачу повышения точности определения температурной зависимости коэффициента теплопроводности твердых, изотропных электропроводящих материалов.
Поставленная техническая задача решается тем, что в способе определения температурной зависимости коэффициента теплопроводности твердых, изотропных электропроводящих материалов, включающем нагрев пропусканием постоянного тока по двум полым цилиндрическим образцам с разной толщиной стенки, в которых реализуется одномерное поле температуры по толщине, измерение на изотермическом участке длиной L силы тока I, падения напряжения U и истинной температуры внутренней поверхности Т для каждого цилиндра, построение зависимостей плотности теплового потока с единицы поверхности от температуры q1=f(T1), q2=f(T2) и определение истинных температур внутренней поверхности двух полых цилиндрических образцов Т1 и T2 при одинаковых значениях q1=q2=qs, вычисление значений коэффициента теплопроводности в предположении, что свойства материала не зависят от температуры, определение температуры отнесения и построение температурной зависимости коэффициента теплопроводности λ=f(Tотн) в первом приближении, дополнительно из экспериментальных данных по падению напряжения U и силе тока I определяют зависимость коэффициента удельного электрического сопротивления от температуры отнесения ρ(Tотн), данные коэффициента теплопроводности, полученные в первом приближении, обрабатывают в виде линейной функции от температуры отнесения λ=аТотн+b и используют ρ(Tотн) и λ=aTотн+b при численном решении стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты, зависящими от температуры, для заданного числа выбранных значений силы тока Ii и истинной температуры Ti внутренней поверхности одного из двух полых цилиндрических образцов, находят соответствующее число распределений температуры по толщине цилиндрической стенки, для каждого из них вычисляют известным способом новые значения коэффициента теплопроводности и температуры отнесения и окончательно определяют температурную зависимость коэффициента теплопроводности λ1(Tотн) в изучаемом диапазоне температур.
Достигаемым техническим результатом является повышение точности определения температурной зависимости коэффициента теплопроводности по сравнению с прототипом. Поставленная техническая задача решается с учетом найденных экспериментальных данных зависимостей ρ(Тотн) и λ=аТотн+b для выбранного значения силы тока и соответствующей ему внутренней температуры стенки Т с применением численного решения стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты, которые зависят от температуры. Это позволяет определить реальное распределение температуры по цилиндрической стенке и на его основе рассчитать уточненные значения коэффициента теплопроводности и температуры отнесения. Способы определения коэффициента теплопроводности, которые использовали в аналоге и в прототипе, основаны на простых аналитических решениях уравнения теплопроводности, что неизбежно приводит к потере точности. В предлагаемом способе основой для определения коэффициента теплопроводности является дифференциальное уравнение, в котором учитываются реальные функциональные зависимости свойств исследуемого материала от температуры. Данное уравнение может быть решено только численными методами. Предлагаемый способ позволяет проводить эксперимент с тонкостенными цилиндрическими образцами, что приводит к уменьшению перепада температуры по толщине стенки и, следовательно, уменьшает погрешность при осреднении.
Предлагаемый способ осуществляется следующим образом. Предварительно выбирают два тонкостенных цилиндрических образца с разной толщиной стенки, в которых может быть реализовано одномерное приближение для поля температуры. Желательно проводить эксперимент на образцах с одинаковым внешним радиусом. Образцы нагревают постоянным электрическим током. Для каждого из них в стационарном режиме на изотермическом участке измеряют падение напряжения и силу тока. Через специальное отверстие, которое просверлено в центре изотермического участка и которое моделирует абсолютно черное тело, измеряют истинную температуру внутренней поверхности образца. Строят зависимости q1=f(T1), q2=f(T2) и определяют истинные температуры внутренней поверхности двух полых цилиндрических образцов T1 и Т2 при одинаковых значениях плотности теплового потока q1=q2=qs, вычисляют значения коэффициента теплопроводности в предположении, что свойства материала не зависят от температуры, определяют соответствующие значения температуры отнесения и находят температурную зависимость коэффициента теплопроводности λ=f(Tотн) в первом приближении. Дополнительно по электрическим параметрам рассчитывают значения коэффициента удельного электрического сопротивления и определяют его зависимость от температуры отнесения. Данные коэффициента теплопроводности, полученные в первом приближении, обрабатывают в виде линейной функции от температуры отнесения λ=аТотн+b. Эти данные используют при численном решении стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты, зависящими от температуры:
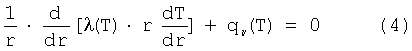
для выбранных значений силы тока Ii, и истинной температуры Тi внутренней поверхности одного из двух полых цилиндрических образцов. Находят соответствующее число распределений температуры по толщине цилиндрической стенки. Для каждого из них вычисляют новые значения коэффициента теплопроводности и температуры отнесения и окончательно определяют температурную зависимость коэффициента теплопроводности λ1(Tотн) в изучаемом диапазоне температур.
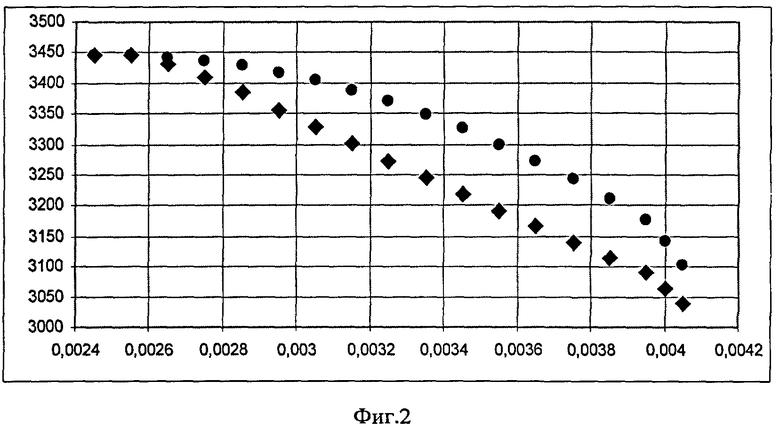
Предлагаемый способ был реализован на образцах графита марки DE-24 размерами D/d=5,9 мм/8,1 мм и D/d=4,9 мм/8,1 мм. Для области температур 2900-3400 К метод двух цилиндров, основанный на предположении о постоянстве свойств, позволил определить в первом приближении зависимость коэффициента теплопроводности от температуры в виде линейной функции λ=-4,6339·10-2 Тотн + 1,6345·102, а из электрических измерений рассчитать зависимость коэффициента удельного электрического сопротивления от температуры отнесения (фиг.1). Численное решение уравнения (4) для выбранного значения силы тока и соответствующей температуры на внутренней поверхности образца позволило найти уточненное распределение поля температуры по толщине цилиндрической стенки (фиг.2). На фиг.2 показано поле температуры в образце графита DE-24 с внешним радиусом R=4,05 мм, внутренним радиусом r=2,45 мм при силе тока I=540 А, которое рассчитано для случая постоянных свойств • -λ, qv=const (прототип), и переменных от температуры свойств ♦ -λ, qv=f(T). Из фиг.2 следует, что учет температурной зависимости свойств дает более высокое значение перепада температуры по толщине стенки и, следовательно, средняя величина коэффициента теплопроводности окажется ниже по сравнению с величиной, которую давал способ-прототип. Например, для температуры 3200 К прототип позволил определить значение коэффициента теплопроводности λ=15,3 Вт/мК, а предлагаемый способ позволил уточнить λ1=12,4 Вт/мК.
Способ применим для электропроводящих материалов, которые имеют выраженную зависимость коэффициентов теплопроводности и удельного электрического сопротивления от температуры, например, в области выше 2800 К для углеграфитовых материалов. Одним из главных преимуществ способа является то, что он реализуется в стационарных условиях, причем для области высоких температур. Это отвечает максимальному приближению к реальным условиям работы высокотемпературных материалов. Возможность применения нестационарных методов исследования для указанной области температур затруднена из-за низкой воспроизводимости переносных свойств графита вообще и коэффициента теплопроводности в частности. Использование в эксперименте тонкостенных образцов, учет температурной зависимости свойств исследуемого материала и численное решение соответствующего уравнения теплопроводности показало, что реальные значения коэффициента теплопроводности могут оказаться на 20-30% ниже по сравнению с величинами, которые давал способ-прототип. Например, для графита отличие значений коэффициента теплопроводности от величин, измеренных способом-прототипом, может составлять 20% в области температур выше 3000 К.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения коэффициента теплопроводности при температурах до 2800 К полупроводниковых, композиционных материалов | 2020 |
|
RU2748985C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ЭЛЕКТРОПРОВОДЯЩИХ МАТЕРИАЛОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ | 2019 |
|
RU2709708C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2009 |
|
RU2387981C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВРЕМЕНИ РЕЛАКСАЦИИ ТЕПЛОВОГО ПОТОКА И ЕГО ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ В ТВЕРДОМ ИЗОТРОПНОМ МАТЕРИАЛЕ | 2009 |
|
RU2415407C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ И ТЕПЛОВОГО СОПРОТИВЛЕНИЯ СТРОИТЕЛЬНОЙ КОНСТРУКЦИИ | 2011 |
|
RU2527128C2 |
| Способ определения температуропроводности и коэффициента теплопроводности | 2022 |
|
RU2785084C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ ТЕЛ | 1990 |
|
RU1766172C |
| СПОСОБ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ МАТЕРИАЛОВ | 2013 |
|
RU2523090C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ ФЛЮИДОНАСЫЩЕННЫХ ПОД ДАВЛЕНИЕМ ПОРИСТЫХ ТЕЛ | 2012 |
|
RU2492455C1 |
| Устройство для измерения теплопроводности горной породы под одновременным воздействием порового и внешнего давлений | 2022 |
|
RU2790201C1 |
Изобретение относится к теплофизическим измерениям. Способ использует, во-первых, экспериментальное определение коэффициента теплопроводности на двух полых цилиндрических образцах с разной толщиной стенки. Во-вторых, в способе используется численное решение стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты и учитывается температурная зависимость коэффициентов теплопроводности и удельного электрического сопротивления. Способ применим для электропроводящих материалов, которые имеют выраженную зависимость коэффициентов теплопроводности и удельного электрического сопротивления от температуры, например, в области выше 2800 К для углеграфитовых материалов. Способ реализуется в стационарных условиях, причем для области высоких температур. Технический результат - повышение точности определения температурной зависимости коэффициента теплопроводности. 2 ил.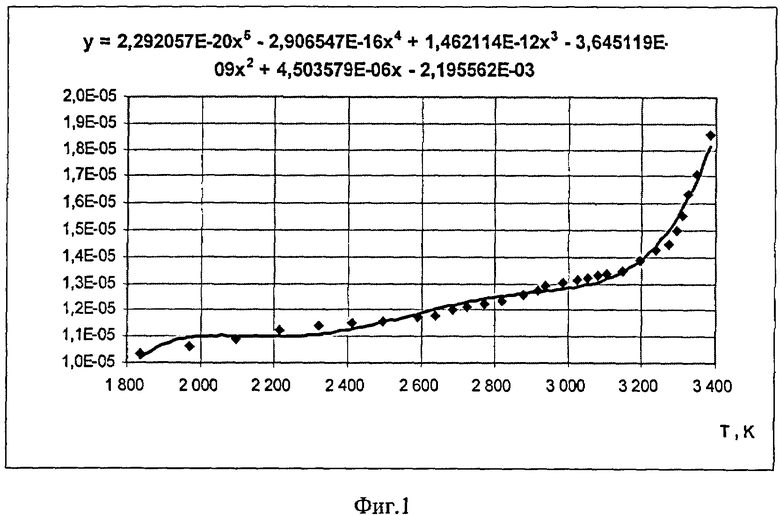
Способ определения температурной зависимости коэффициента теплопроводности твердых изотропных электропроводящих материалов, включающий нагрев образцов пропусканием постоянного тока по двум полым цилиндрическим образцам с разной толщиной стенки, измерение значений силы тока I, падения напряжения U и истинной температуры внутренней поверхности для каждого цилиндра, построение зависимостей плотности теплового потока с единицы поверхности от температуры q1=f(T1), q2=f(T2), и определение истинных температур внутренней поверхности двух полых цилиндрических образцов T1 и Т2 при одинаковых значениях q1=q2=qs, определение значений коэффициента теплопроводности, определение температуры отнесения и построение температурной зависимости коэффициента теплопроводности в первом приближении, отличающийся тем, что для изучаемой области температур определяют в первом приближении зависимость коэффициента теплопроводности от температуры отнесения в виде линейной функции λ=aТотн+b, дополнительно по падению напряжения U и силе тока I определяют зависимость коэффициента удельного электрического сопротивления от температуры отнесения ρ(Тотн), и используют ρ(Тотн) и λ=aТотн+b при численном решении стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты, зависящими от температуры, для выбранных значений силы тока I и истинной температуры Т внутренней поверхности одного из двух полых цилиндрических образцов находят реальное распределение температуры по толщине цилиндрической стенки, на его основе определяют уточненные значения коэффициента теплопроводности и температуры отнесения и окончательно определяют температурную зависимость коэффициента теплопроводности в изучаемой области температур.
| ПЕТРОВ В.А | |||
| Излучательная способность высокотемпературных материалов | |||
| - М.: Наука, 1969, с.28 | |||
| Сплав на медной основе для изготовления радиаторных трубок | 1944 |
|
SU66055A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ ТЕПЛОПРОВОДНОСТИ ВЫСОКОТЕМПЕРАТУРНОЙ СВЕРХПРОВОДЯЩЕЙ J, - BA - CU - O КЕРАМИКИ | 1992 |
|
RU2009558C1 |
| Способ определения температурной зависимости температуропроводности материалов | 1990 |
|
SU1749801A1 |
| JP 2009128318 A, 11.06.2009. | |||
Авторы
Даты
2011-05-27—Публикация
2009-08-06—Подача