Изобретение относится к измерительной технике и может быть использовано в измерительных приборах и системах с целью преобразования измеряемых аналоговых величин в цифровую форму для последующей обработки и представления в удобном для экспериментатора виде.
Аналого-цифровое преобразование является важной частью процесса измерения, и создание новых способов такого преобразования, более простых, надежных, с улучшенными метрологическими характеристиками, имеет существенное значение, особенно при разработке автоматизированных систем для научных и экспериментальных исследований.
Известен компенсационный способ преобразования и цифрового измерения [1] , при котором путем уравновешивания ЭДС нормального элемента на образцовом сопротивлении устанавливается рабочий ток, затем уравновешивается измеряемая величина с помощью декадных магазинов сопротивлений и цифровое значение измеряемой величины определяется по положению ручек декадных магазинов после уравновешивания.
Однако указанный способ трудоемок, требует постоянного участия экспериментатора в процессе измерения и затрудняет последующую обработку измерительной информации.
Кроме того, известен способ преобразования аналоговой величины в код [2], являющийся прототипом предлагаемого изобретения и заключающийся в том, что преобразуемую величину сравнивают путем уравновешивания с дискретно изменяющейся по определенному алгоритму образцовой величиной. Обычно используют либо развертывающее уравновешивание, при котором образцовая величина автоматически увеличивается с каждым шагом на одну минимальную ступень до совпадения образцов и преобразуемой величин, либо поразрядное кодирование, при котором ступени образцовой величины образуют ряд в соответствии с позиционной системой счисления, как правило, двоичной, либо совпадение, при котором сравнение преобразуемой величины происходит одновременно и параллельно со всеми значениями образцовой величины.
В результате по совпадению преобразуемой и образцовой величин определяют цифровой код преобразуемой величины.
Однако указанный способ, реализующий наиболее простое уравновешивание путем развертывающего преобразования, требует большого числа тактов уравновешивания и имеет поэтому малое быстродействие. Если значение преобразуемой величины U, а погрешность преобразования ΔU, то число тактов уравновешивания определяется простым соотношением:
N1 = U/ΔU (1)
При осуществлении способа на основе совпадения, который является самым быстродействующим, требуется одновременного и параллельное выполнение большого числа сравнений. Преобразование совершается за один такт, но при тех же значениях U и Δ U необходимо выполнять одновременно N1 сравнений, поэтому требуется в N1 раз больше элементов преобразователя по сравнению с развертывающим уравновешиванием, что усложняет реализацию такого способа.
Целью изобретения является упрощение процесса преобразования.
Цель достигается за счет уменьшения числа последовательно выполняемых сравнений.
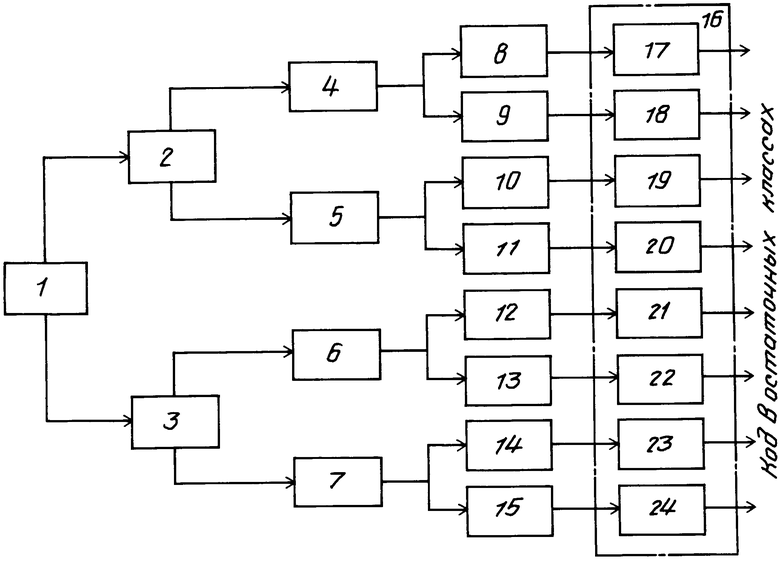
На чертеже показана блок-схема устройства, реализующего данный способ.
Устройство содержит источник 1 преобразуемой величины, модульные преобразователи 2-15, блок 16 из аналого-цифровых преобразователей 17 - 24.
Способ осуществляется следующим образом.
Преобразуемая величина U от источника 1 поступает на модульные преобразователи 2 - 15, причем значения образцовых мер таковы, что U1/ΔU, U2/ ΔU,..., Un/ ΔU являются целыми взаимно простыми числами, где ΔU - минимальный дискретный шаг, определяющий точность преобразования. В результате сравнения модульные преобразователи выделяют остатки Vi = U - Ki Ui < Ui, i = 1,2,...,n, где Ki - некоторые целые числа, значение которых определять не требуется. С выхода этих преобразователей величины остатков Vi поступают на вход блока 16 аналого-цифровых преобразователей, которые преобразуют аналоговые величины Vi в их дискретные значения с минимальным шагом Δ U. В результате имеем набор значений [V1,V2,...Vn], который и является цифровым кодом преобразуемой величины.
Покажем, что такой цифровой код однозначно определяет значение преобразуемой величины. Для доказательства воспользуемся аппаратом многомодульной арифметики вычетов (см., например, Грегори Р., Кришнамурти Е. Безошибочные вычисления. Методы и приложения. М.:, Мир, 1988).
Ключевым в арифметике вычетов является понятие модуля, и отношения между целыми числами выражаются в том, сравнимы они по модулю или нет. Если a сравнимы с b по модулю m, что записывается, как
a ≡ b(мod m), (2) это означает, что при целочисленном делении на m,a и b дают один и тот же остаток r.
Например, числа 2, 7, 12,... 5q+2, где q принимает значение любого целого числа, образуют класс чисел, сравнимых по модулю m = 5, так как все они при делении на 5 дают остаток r = 2. Каждое число класса называется вычетом по модулю m, а r является наименьшим неотрицательным вычетом.
Многомодульная арифметика оперирует с множеством модулей
β  [m1,m2, ... mn] (3)
[m1,m2, ... mn] (3)
Если модули попарно взаимно просты, то β называют базисным вектором. В этом случае каждое число S в диапазоне до
M = 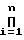 mi (4) может быт однозначно представлено вычетами по соответствующим модулям:
mi (4) может быт однозначно представлено вычетами по соответствующим модулям: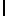 S
S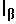 = [
= [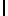 S
S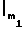 ,
, 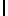 S
S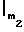 , ...
, ...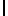 S
S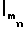 ] (5) Например, если β= 5,7,9, то М = 315, и стандартное представление числа 41 по отношению к заданному базисному вектору выгляди так: |41|β= [1, 6, 5].
] (5) Например, если β= 5,7,9, то М = 315, и стандартное представление числа 41 по отношению к заданному базисному вектору выгляди так: |41|β= [1, 6, 5].
Между множеством Iм = {0,1,2,...М-1} наименьших неотрицательных вычетов по модулю Мм и множеством Iβ=|S|β:Sε], состоящим из М элементов |S|β, где S - любое число натурального ряда, имеется взаимно однозначное соответствие, т. е. многомодульная арифметика вычетов с базисным вектором β эквивалентна одномодульной арифметике вычетов с модулем М, и по остаткам от деления неизвестного числа на модули можно в определенном диапазоне восстановить его значение, т. е. по стандартному представлению числа в виде (S)β найти его единственное значение (S)м.
Один из возможных алгоритмов основан на представлении целых чисел в системе счисления со смешанным основанием.
В общем виде смешанное основание некоторой системы счисления может быть представлено множеством n целых чисел:
ρ= [r1, r2,...,rn] (6) где ri - основания системы. Здесь и далее будем пользоваться обозначениями, принятыми в теории чисел 1,2. Максимальное число, которое может быть записано с помощью (6), составляет
R =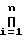 ri, (7) и если 0≅S < R, то S можно представить в виде:
ri, (7) и если 0≅S < R, то S можно представить в виде:
S = do + d1˙ (r1)+d2(r1 ˙r2)+...+ dn-1(r1 r2...rn-1), (8) где do, d1, d2,...,dn-1 - цифры соответственно в нулевом, первом и т.д. разрядах, а сомножители в скобках определяют цену разрядов. Например, при r1 = r2 =...=rn = 10 имеем обычную десятичную систему счисления, и
S = do + d1(10) + d2(102) +...+ dn-1(10n-1) (9) Форма записи числа S в системе ρ выглядит так:
<S>ρ = < do, d1,...,dn-1 > (10)
Если, например, ρ = [2, 3, 5], а <S>ρ =< 1,2,3>, то в стандартной десятичной форме в соответствии с (8)
S = 1 + 2 ˙(2) + 3˙ (2 ˙3) = 23.
Выберем такую систему счисления, что ρ=β. Тогда из (3,4,6,7) следует, что r1 = mi, R = М, т.е. многомодульная система вычетов и система со смешанным основанием оперируют с одним и тем же диапазоном целых чисел. Любое целое число из этого диапазона может быть выражено в виде (5) или (8). Пусть задано (S)β (5), требуется найти <S>β (10).
Обозначив S = t1 и учитывая r1 = mi, из (8) имеем
t1 = dо + m1[d1 + d2(m2) +...+dn-1(m2...mn-1)] = do + m1t2 (11) Тогда (t1)m1 = (S)m1 = do, т.е. первые цифры в (S)β и <S>βсовпадают.
Записывая аналогичные (11) выражения для t2,...,tn, получаем рекурсивную процедуру, дающую все цифры <S> β:
ti+1 = (ti-di-1)/mi; di = |ti+1 | mi+1;
i = 1,2,...,n (12)
Рассмотрим пример. Пусть в системе с β= 3, 5, 7 получено значение |S|β= 1, 0, 5. Определим <S>β и S.
В соответствии с (11) (t1)β=|S|β=[1,0,5] и do = (S)3 = 1. Для нахождения d1 вычисляем t2 на основании (12). Сначала запишем числитель:
(t1 - do)β= [1,0,5] - [1,1,1] = [0, -1,4] = [0,4,4] (покомпонентное вычитание и замена отрицательного вычета на ему протипоположный по соответствующему модулю). Вводя сокращенный базисный вектор β1 = [5,7], имеем (t1-do)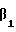 = [4,4]. Чтобы разделить на m1, надо найти обратный по β1 элемент m1-1 (β1 ) = [3-1(5), 3-1(7)]. Обратный по модулю элемент определяется их условия (S˙ S-1)m = 1. Следовательно, 3-1( β1) = [2,5].
= [4,4]. Чтобы разделить на m1, надо найти обратный по β1 элемент m1-1 (β1 ) = [3-1(5), 3-1(7)]. Обратный по модулю элемент определяется их условия (S˙ S-1)m = 1. Следовательно, 3-1( β1) = [2,5].
Отметим, что существует универсальные алгоритмы для определения обратных по модулю значений, однако здесь не будем на них останавливаться, а ограничимся проверкой: |3 ˙2|5 = 1 и |3˙ 5|7 = 1. В таких простых случаях обратные величины легко определяются перебором.
Теперь можно найти t2:
(t2)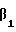 = (t1-do)
= (t1-do)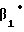 m-1(β1)=[4,4]˙ [2,5]=[3,6] (покомпонентное умножение и определение вычетов по соответствующим модулям). Следовательно, d1 = 3. Для получения последней цифры представления <S>β повторяем процедуру (12) для i = 2:
m-1(β1)=[4,4]˙ [2,5]=[3,6] (покомпонентное умножение и определение вычетов по соответствующим модулям). Следовательно, d1 = 3. Для получения последней цифры представления <S>β повторяем процедуру (12) для i = 2:
(t2-d1)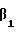 = [3.6] - [3.3] = [0.3];
= [3.6] - [3.3] = [0.3];
β2= [7]; (t2-d1)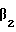 = [3];
= [3];
m
(t3)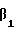 = [3]·[3]= [9]7 = [2]
= [3]·[3]= [9]7 = [2]
В итоге получаем d3 = 2, и искомое представление числа ρ в системе счисления со смешанным основанием [3, 5, 7] имеет вид: <S>β=<1,3,2>. Само число S, как следует из (8), равно S = 1 + 3˙(3) + 2˙ (3 ˙5) = 40.
Таким образом, по остаткам от целочисленного деления числа на 3, 5, 7 восстановлено его значение 40.
Проиллюстрируем измерительную интерпретацию многомодульной арифметики вычетов на численном примере.
Пусть преобразуемая величина имеет значение 84,0007 В, или в целочисленном эквиваленте 840007. Это напряжение поступает параллельно на два модульных преобразователя 2 и 3 с модулями m1 и m2.
Пусть m1 = 907, m2 = 1109. Числа должны быть взаимно простыми, а их произведение - обеспечивать заданный диапазон, в данном случае 106 (100 В с точностью до кванта 0,1 мВ). Модули m1 и m2 соответствуют значениям напряжений 90,7 мВ и 110,9 мВ. Нам выходе модульных преобразователей МОД m1 и МОД m2 в результате сравнения получаем остатки 12,5 мВ и 49,44 мВ (целочисленные эквиваленты 125 и 494). Каждое из этих остаточных напряжений поступает параллельно на модульные преобразователи 4 и 5, 6 и 7, с модулями l1 и l2 (l1 = 31, l2 = 37, что соответствует напряжением 3,1 мВ и 3,7 Мв), на выходе которых имеем две пары остаточных напряжений 0,1 мВ и 1,4 мВ, 2,9 мВ и 1,3 мВ (целочисленные эквиваленты 1 и 14, 29 и 13). Каждое из четырех остаточных напряжений поступает параллельно на модульные преобразователи 8 и 9, 10 и 11, 12 и 13, 14 и 15 с модулями t1 и t2 (t1 = 6, t2 = 7), что соответствует напряжениям 0,6 мВ и 0,7 мВ. На выходе имеем четыре пары остаточных направлений 0,1 мВ и 0,1 мВ, 0,2 мВ и 0,0 мВ , 0,5 мВ и 0,1 мВ, 0,1 мВ и 0,6 мВ. Каждое из последних остаточных напряжений поступает на блок 16 аналого-цифровых преобразователей (разрядность которых существенно меньше, чем в преобразователе по известному способу). В итоге получаем цифровой код преобразуемого напряжения в виде восьми вычетов по модулям 6 и 7:
[1,1], [2,0], [5,1], [1,6] (13)
Покажем, как от этого цифрового кода однозначно перейти к преобразуемому значению.
Решение для модулей 6 и 7 запишется в виде сравнения
S1 = 7 b1 + 36 b2 (mod 42) (14) Подставляя в качестве b1 и b2 значения вычетов (1), получаем четыре вычета по модулю 42:
[1,14], [29,13] (15)
Целочисленные значения (15) - это остатки, полученные на предпоследнем шаге сравнения. Здесь используются модули 31 и 37, и решением для них является сравнение
S2 = 962 b1 + 186 b2 (mod 1146) (16)
Подставляя в (16) вместо b1 и b2 их значения из (15), имеем два вычета по модулю 1147:
[125,494] (17)
Это целочисленные остатки, полученные на первом шаге сравнения по модулям 907 и 1109. И, наконец, сравнение, дающее результат в привычной десятичной системе, выглядит так: S3 = 253961 b1 + 751903 b2 (mod 1005863) (18) Вычисляя S3 при b1 = 125 и b2 = 194, получим целочисленный эквивалент преобразуемого напряжения 840007, что при переходе к именованному числу дает окончательный результат 84,0007 В. Таким образом, данный способ аналого-цифрового преобразования позволяет упростить процесс преобразования по сравнению с прототипом за счет уменьшения числа необходимых сравнений в 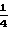
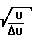 раз, где U - преобразуемая величина; Δ U - погрешность преобразования.
раз, где U - преобразуемая величина; Δ U - погрешность преобразования.
Изобретение относится к информационно-измерительной технике, в частности к цифровым преобразованиям аналоговых величин. Цель изобретения - упрощение процесса преобразования. Способ основан на выборе для сравнения таких значений образцовых мер, которым могут быть поставлены в соответствие целые взаимно простые числа, и на определении остатков от деления преобразуемой величины на значения образцовых мер, которые после аналого-цифрового преобразования являются цифровым кодом преобразуемой величины. При этом уменьшается число сравнений. 1 ил.
СПОСОБ ПРЕОБРАЗОВАНИЯ АНАЛОГОВОЙ ВЕЛИЧИНЫ В КОД, заключающийся в сравнении путем уравновешивания преобразуемой величины с дискретно изменяющимися образцовыми мерами и формировании кода, отличающийся тем, что, с целью упрощения процесса преобразования, в качестве образцовых мер используют целые взаимно простые числа, а формирование кода осуществляют путем аналого-цифрового преобразования остатков от целочисленного деления преобразуемой величины на значения образцовых мер.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Шляндин В.М | |||
| Цифровые измерительные устройства | |||
| М.: Высшая школа, 1981, с.228. | |||
Авторы
Даты
1994-09-30—Публикация
1990-05-21—Подача