Изобретение относится к области автоматики и вычислительной техники и может быть использовано в цифровых вычислительных устройствах для выполнения операции деления числа в модулярном коде на одно из оснований модулярной системы счисления (МСС).
Известно устройство (аналог) (авт. св. СССР №1683013А1, МКИ G 06 F 7/72, Б.И. №37, 1991 г.), содержащее регистры делимого и делителя, регистр сдвига и вспомогательный регистр, блоки вычитания, умножения и сложения, параллельно-конвейерный формирователь интегральных характеристик модулярного кода, счетчик, элемент ИЛИ-НЕ, элемент задержки, регистр частного и элемент ИЛИ.
Недостаток устройства - низкое быстродействие выполнения операции деления числа в МСС.
Наиболее близким по технической сущности (прототипом к предлагаемому изобретению) является устройство (авт. св. СССР №1667066 А1, МКИ G 06 F 7/72, Б.И. №28, 1991 г.), содержащее блок элементов задержки, блок вычисления интервального индекса числа, элемент задержки, первый и второй регистры сдвига, регистр модулярного кода числа, блоки мультиплексоров, блоки хранения констант, блок управления, первый и второй блоки элементов ИЛИ.
Недостаток прототипа - низкое быстродействие выполнения операции деления числа в МСС вследствие ограниченного быстродействия полупроводниковых логических элементов, из которых состоит данное устройство.
Цель изобретения состоит в повышении производительности перспективных образцов вычислительной техники.
Технический результат выражается в повышении быстродействия выполнения операции деления числа в модулярном коде на одно из оснований МСС.
Поставленная цель достигается тем, что в устройство, содержащее регистр модулярного кода числа, N входов которого являются входами устройства (N - число оснований МСС), введены (N-1) табличных вычислителей, преобразователь модулярного кода в полиадический код, (N-1) устройств отображения и сумматор (N-1) чисел по модулю mN (mN - основание, на которое осуществляется деление числа в МСС), причем i-ый выход регистра модулярного кода числа 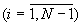 соединен с первым входом i-го табличного вычислителя, ко второму входу которого подключен N-ый выход регистра модулярного кода числа, выход i-го табличного вычислителя является i-ым выходом устройства и соединен с i-ым входом преобразователя модулярного кода в полиадический код, i-ый выход которого через i-ое устройство отображения соединен с i-ым входом сумматора (N-1) чисел по модулю mN, выход которого является N-ым выходом устройства.
соединен с первым входом i-го табличного вычислителя, ко второму входу которого подключен N-ый выход регистра модулярного кода числа, выход i-го табличного вычислителя является i-ым выходом устройства и соединен с i-ым входом преобразователя модулярного кода в полиадический код, i-ый выход которого через i-ое устройство отображения соединен с i-ым входом сумматора (N-1) чисел по модулю mN, выход которого является N-ым выходом устройства.
В основу функционирования предлагаемого устройства положены следующие принципы.
Признаком деления нацело числа А, представленного в модулярном коде A=(α 1, α 2,... , α N) 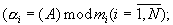 mi - i-oe основание МСС), на основание mN является равенство нулю сравнения α N=AmodmN ≡ 0 [1, с.146-147]. Если α N ≠ 0, то можно рассматривать деление числа А-α N=А-AmodmN, что эквивалентно округлению результата деления до целого значения в меньшую сторону. Значения остатков γ i модулярного кода частного (А-α N)/mN по основаниям
mi - i-oe основание МСС), на основание mN является равенство нулю сравнения α N=AmodmN ≡ 0 [1, с.146-147]. Если α N ≠ 0, то можно рассматривать деление числа А-α N=А-AmodmN, что эквивалентно округлению результата деления до целого значения в меньшую сторону. Значения остатков γ i модулярного кода частного (А-α N)/mN по основаниям 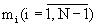 определяются [1, с.147] делением их на число (mN)modmi, т.е.
определяются [1, с.147] делением их на число (mN)modmi, т.е.
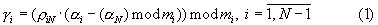
где ρ iN - заранее определяемая константа, которая находится из решения сравнения (ρ iNmN)modmi ≡ 1. Данная операция легко реализуется в табличных вычислителях.
Основная проблема состоит в раскрытии неопределенности вида 0/0 при делении остатка по N-ому основанию на mN. Данная неопределенность раскрывается следующим образом. Известно [1, с.12-13], что число А находится в диапазоне 0≤ A≤ M, где  Тогда число (A-α N)/mN находится в диапазоне
Тогда число (A-α N)/mN находится в диапазоне

С другой стороны, число (А-α N)/mN может быть представлено в полиадическом позиционном коде [2, с.21-22]
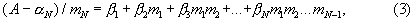
где 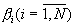 - разряды полиадического кода
- разряды полиадического кода 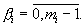
Разряды полиадического кода определяются по остаткам модулярного кода γ i в соответствии с выражениями [2, с.21-22]
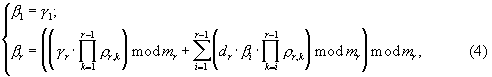
где ρ k,r - обратная мультипликативная величина, определяемая из решения сравнения (ρ r,k·mk)modmr ≡ 1; dr=mr-1; 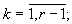
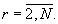
Из анализа выражения (3) следует, что если β N=0, а 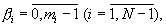 то максимальное значение числа в этом случае будет равно М/mN-1. Таким образом, из (2), (3) и (4) следует, что в полиадическом коде числа (A-α N)/mN старший разряд β N=0, а для определения разрядов
то максимальное значение числа в этом случае будет равно М/mN-1. Таким образом, из (2), (3) и (4) следует, что в полиадическом коде числа (A-α N)/mN старший разряд β N=0, а для определения разрядов 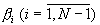 необходимо знать только остатки результата деления числа (А-α N)/mN по основаниям m1, m2,... , mN-1,которые могут быть вычислены в табличных вычислителях.
необходимо знать только остатки результата деления числа (А-α N)/mN по основаниям m1, m2,... , mN-1,которые могут быть вычислены в табличных вычислителях.
На основании изложенного выше получаем
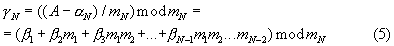
Следовательно, расчет γ N состоит в определении разрядов 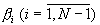 полиадического кода числа, код которого в МСС равен (γ 1, γ 2,... , γ N-1), и суммировании по модулю mN этих разрядов, умноженных на соответствующие весовые коэффициенты, по формуле (5).
полиадического кода числа, код которого в МСС равен (γ 1, γ 2,... , γ N-1), и суммировании по модулю mN этих разрядов, умноженных на соответствующие весовые коэффициенты, по формуле (5).
Таким образом, сущность изобретения заключается в определении в (N-1) табличных вычислителях по основаниям 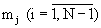 остатков γ j результата деления на основание mN числа А, расчете остатка γ N путем получения из остатков γ j разрядов полиадического кода β j, в преобразователе модулярного кода и сложении этих разрядов с учетом весовых коэффициентов в сумматоре (N-1) чисел по модулю mN.
остатков γ j результата деления на основание mN числа А, расчете остатка γ N путем получения из остатков γ j разрядов полиадического кода β j, в преобразователе модулярного кода и сложении этих разрядов с учетом весовых коэффициентов в сумматоре (N-1) чисел по модулю mN.
Для получения γ N представим значения остатков (γ 1, γ 2,... , γ N-1) числа (А-α N)/mN фазой гармонического сигнала. Суммируя фазы этого сигнала в соответствии с алгоритмом преобразования чисел из модулярного кода в полиадический (4), определяем разряды полиадического кода путем измерения суммарного набега фазы и затем, повторно кодируя фазы гармонического сигнала в соответствии со значениями разрядов полученного полиадического кода, определяем остаток γ N, который будет прямо пропорционален суммарному набегу фазы.
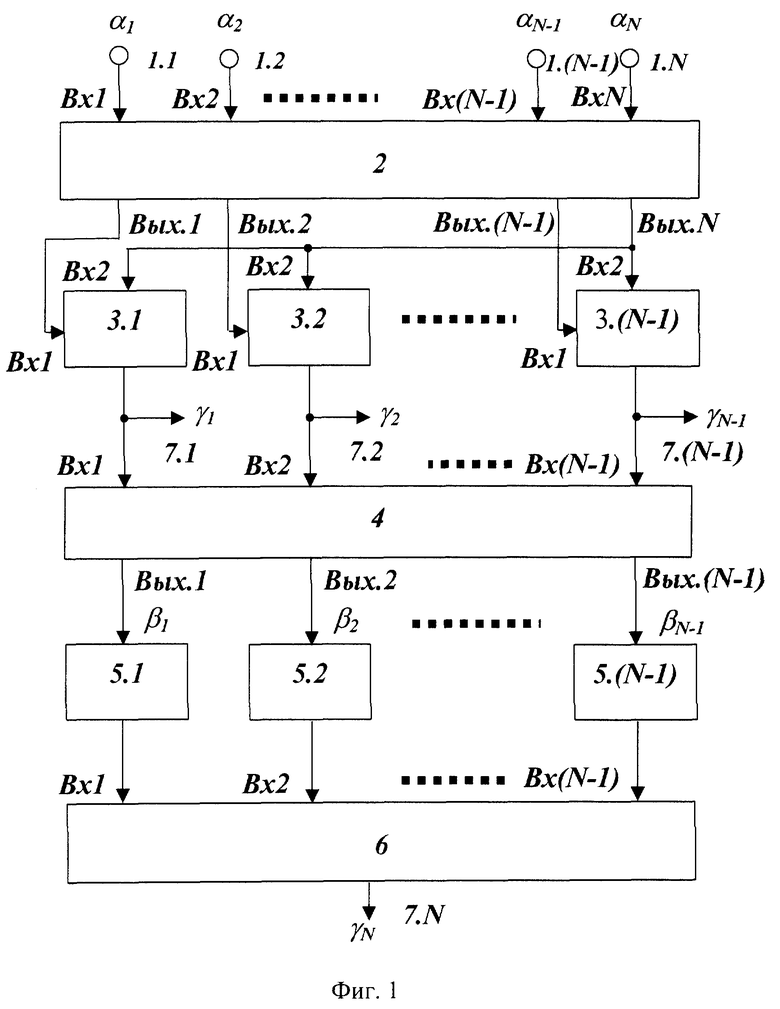
Структурная схема устройства, реализующего изложенный алгоритм, представлена на фиг.1.
В данной схеме 1.1-1.N - входы устройства (N - число оснований МСС), 2 - регистр модулярного кода числа, 3.1-3.(N-1) - табличные вычислители, 4 - преобразователь модулярного кода в полиадический код, 5.1-5.(N-1) - устройства отображения, 6 - сумматор (N-1) чисел по модулю mN, 7.1-7.N - выходы устройства.
Входы устройства 1.1-1.N соединены с информационными входами Bx1-BxN регистра модулярного кода числа 2. Выходы 1-(N-1) регистра модулярного кода числа подключены ко входам 1 табличных вычислителей 3.1-3.(N-1) соответственно, а выход N регистра модулярного кода числа 2 соединен со входами 2 табличных вычислителей 3.1-3.(N-1), выходы которых подключены ко входам 1-(N-1) преобразователя модулярного кода в полиадический код 4, выходы 1-(N-1) которого через устройства отображения 5.1-5.(N-1) подключены ко входам 1-(N-1) сумматора по модулю mN 6, выход которого является выходом устройства 7.N, а выходы табличных вычислителей 3.1-3.(N-1), соответственно, являются выходами 7.1-7.(N-1) устройства.
Реализация основных узлов устройства представлена на фиг.2 и 3.
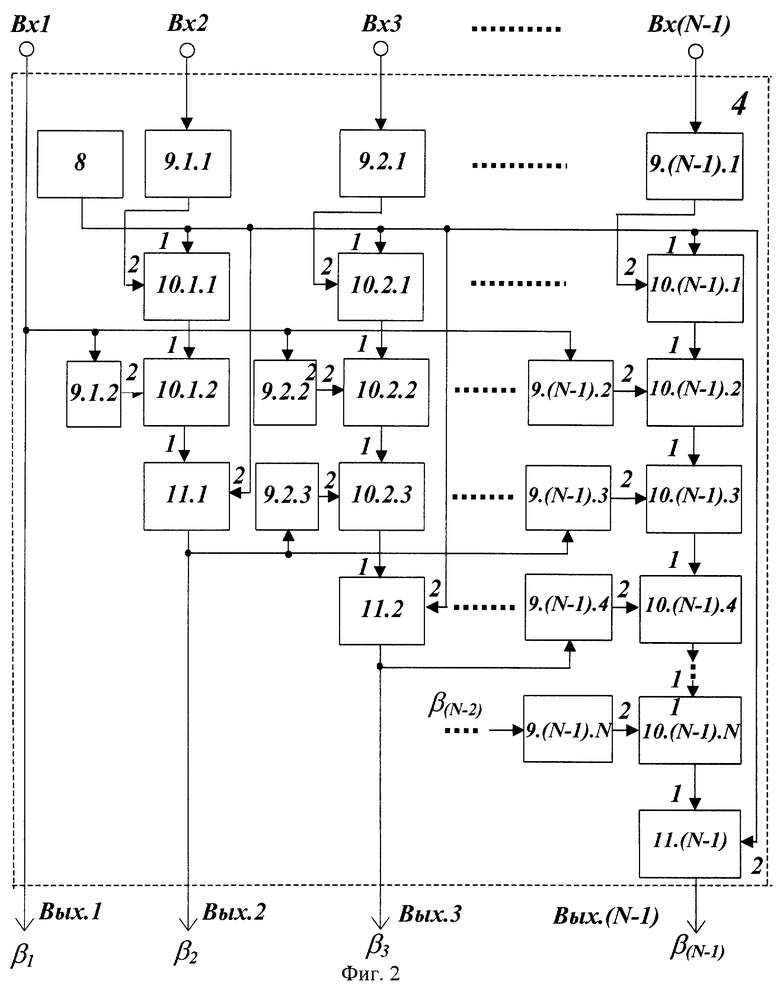
На фиг.2 представлена структурная схема преобразователя модулярного кода в полиадический код 4, где 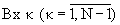 – входы преобразователя, 8 - генератор гармонического сигнала, 9.1.1-9.(N-1).N - устройства отображения, 10.1.1-10.(N-1).N - управляемые фазовращатели, 11.1-11.(N-1) - измерители сдвига фазы, Вых к - выходы преобразователя.
– входы преобразователя, 8 - генератор гармонического сигнала, 9.1.1-9.(N-1).N - устройства отображения, 10.1.1-10.(N-1).N - управляемые фазовращатели, 11.1-11.(N-1) - измерители сдвига фазы, Вых к - выходы преобразователя.
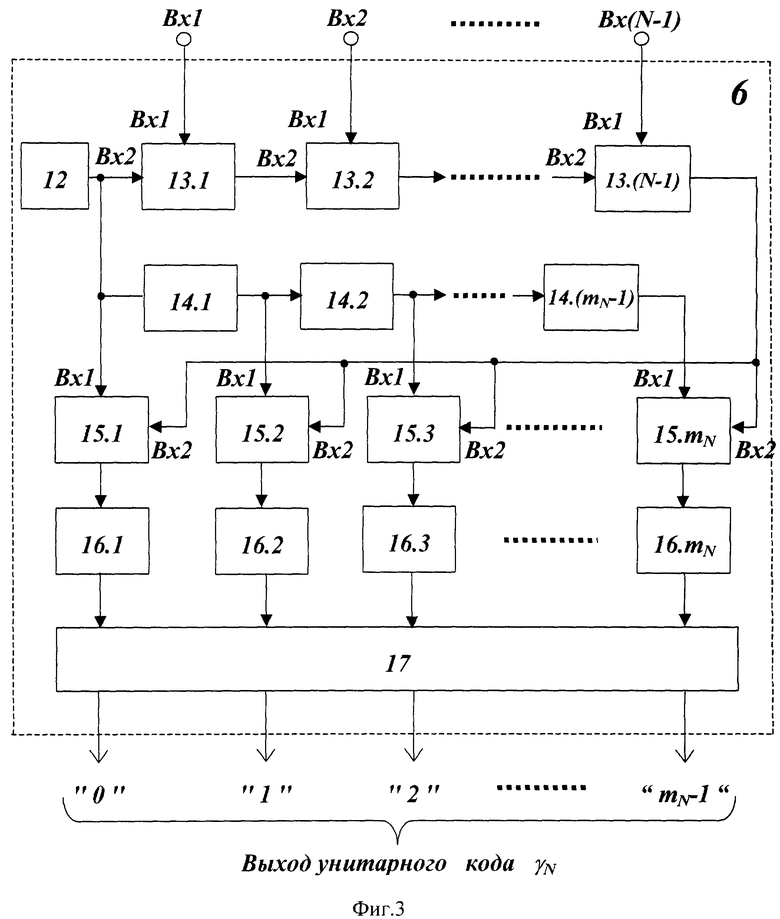
На фиг.3 представлена структурная схема сумматора по модулю mN 6, где 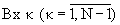 - входы устройства, 12 - генератор гармонического сигнала, 11.1-11.N - управляемые фазовращатели, 14.1-14.(mN-1) – линии задержки на время
- входы устройства, 12 - генератор гармонического сигнала, 11.1-11.N - управляемые фазовращатели, 14.1-14.(mN-1) – линии задержки на время 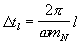 (где
(где 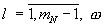 - частота генератора гармонического сигнала), 15.1-15.mN - аналоговые перемножители, 16.1-16.mN - интеграторы, 17 - схема выбора максимума.
- частота генератора гармонического сигнала), 15.1-15.mN - аналоговые перемножители, 16.1-16.mN - интеграторы, 17 - схема выбора максимума.
Рассмотрим работу устройства.
Остатки (α 1, α 2,... , α N) числа А в МСС подаются на информационные входы 1.1-1.N и записываются в регистр модулярного кода числа 2. С выходов 1-(N-1) регистра модулярного кода числа остатки 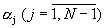 в унитарном коде поступают на первые входы табличных вычислителей 3.1-3.(N-1), на вторые входы которых поступает сигнал с выхода N регистра модулярного кода числа 2. В j-ых табличных вычислителях
в унитарном коде поступают на первые входы табличных вычислителей 3.1-3.(N-1), на вторые входы которых поступает сигнал с выхода N регистра модулярного кода числа 2. В j-ых табличных вычислителях  определяются остатки γ j модулярного кода частного (А-α N)/mN по основаниям
определяются остатки γ j модулярного кода частного (А-α N)/mN по основаниям 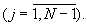 Полученные остатки поступают на выходы устройства 7.j и на соответствующие входы преобразователя модулярного кода числа в полиадический код 4, где сигнал со входа 1 следует непосредственно на выход 1 преобразователя и на входы устройств отображения 9.1.2-9.(N-1).2, а со входов 2-(N-1) на устройства отображения 9.1.1-9.(N-1).1. В устройствах отображения 9.j.1
Полученные остатки поступают на выходы устройства 7.j и на соответствующие входы преобразователя модулярного кода числа в полиадический код 4, где сигнал со входа 1 следует непосредственно на выход 1 преобразователя и на входы устройств отображения 9.1.2-9.(N-1).2, а со входов 2-(N-1) на устройства отображения 9.1.1-9.(N-1).1. В устройствах отображения 9.j.1 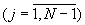 в соответствии с формулой (4) осуществляется унарное преобразование
в соответствии с формулой (4) осуществляется унарное преобразование 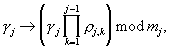 а в устройствах отображения 9.j.2 - унарное преобразование
а в устройствах отображения 9.j.2 - унарное преобразование 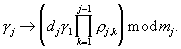 Сигналы с выходов устройств отображения 9.j.1 и 9.j.2 поступают на Вх2 управляемых фазовращателей 10.1.j и 10.2.j
Сигналы с выходов устройств отображения 9.j.1 и 9.j.2 поступают на Вх2 управляемых фазовращателей 10.1.j и 10.2.j 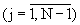 соответственно, где устанавливаются набеги фазы, пропорциональные
соответственно, где устанавливаются набеги фазы, пропорциональные 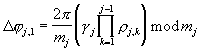 и
и 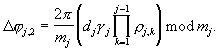 Гармонический сигнал с выхода генератора 8 будет иметь на выходе УФ 10.1.2 суммарный набег фазы, прямо пропорциональный значению разряда полиадического кода β 2. В измерителе сдвига фазы 11.1 эта фаза сравнивается с фазой опорного сигнала с выхода ГГС 8, и на выходе формируется унитарный код разряда
Гармонический сигнал с выхода генератора 8 будет иметь на выходе УФ 10.1.2 суммарный набег фазы, прямо пропорциональный значению разряда полиадического кода β 2. В измерителе сдвига фазы 11.1 эта фаза сравнивается с фазой опорного сигнала с выхода ГГС 8, и на выходе формируется унитарный код разряда
β 2=((γ 2ρ 2,1)modm2+(d2β 1ρ 2,1)modm2)modm2,
который поступает на Вых2 преобразователя 4 и на устройства отображения 9.2.3-9.(N-1).3. Аналогично формируются разряды унитарного кода β 3-β (N-1), которые поступают на Bых3-(N-1) преобразователя 4 соответственно.
Сформированный полиадический код, через устройства отображения 5.j 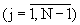 осуществляющих соответственно унарные преобразования
осуществляющих соответственно унарные преобразования
β 1 → (β 1)modmN,
β 2 → (β 2·m1)modmN,...
β N-1 → (β N-1·m1m2...mN-2)modmN,
поступает на Bx1-Bx(N-1) сумматора (N-1) чисел по модулю mN 6. В сумматоре 6 в управляемых фазовращателях 13.j 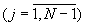 устанавливаются соответствующие сдвиги фазы Δ ϕ j:
устанавливаются соответствующие сдвиги фазы Δ ϕ j:
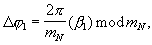
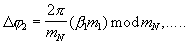
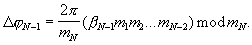
После прохождения гармонического сигнала с выхода генератора 12 на выходе управляемого фазовращателя 13.(N-1) будет суммарный набег фазы
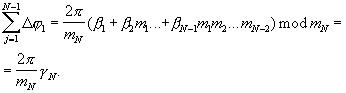
На выходах линий задержки 14.1 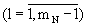 сдвиг фазы гармонического сигнала, соответственно, будет равен
сдвиг фазы гармонического сигнала, соответственно, будет равен 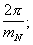
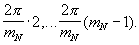 В результате перемножения в перемножителях 15.1-15.mN гармонических сигналов с выхода управляемого фазовращателя 13.(N-1) и с выходов линий задержки 14.l и последующего интегрирования результатов произведения в интеграторах 16.1-16mN образуются постоянные напряжения разного уровня. При этом максимальное напряжение будет на выходе интегратора 75.Z, где Z=γ N+1. В схеме выбора максимума 17 определяется интегратор с наибольшим откликом и результат γ N в унитарном коде поступает на выход сумматора 6, и, соответственно, на выход 7.N устройства.
В результате перемножения в перемножителях 15.1-15.mN гармонических сигналов с выхода управляемого фазовращателя 13.(N-1) и с выходов линий задержки 14.l и последующего интегрирования результатов произведения в интеграторах 16.1-16mN образуются постоянные напряжения разного уровня. При этом максимальное напряжение будет на выходе интегратора 75.Z, где Z=γ N+1. В схеме выбора максимума 17 определяется интегратор с наибольшим откликом и результат γ N в унитарном коде поступает на выход сумматора 6, и, соответственно, на выход 7.N устройства.
Сравним быстродействие прототипа и предлагаемого устройства.
В прототипе время получения остатка равно
ТПР=(]log2N[+2)·tMT,
где ]• [ - символ округления в большую сторону; tМТ - длительность модульного такта устройства, которая не может быть меньше длительности переключения логического элемента tЛЭ ≈ 10-10С [3, с. 173]. Реально tМТ на порядок больше tЛЭ, то есть tМТ ≈ 10-9С.
Таким образом, ТПР ≈ 10-9·(]log2N[+2), C.
В предлагаемом устройстве время вычисления модулярного кода частного ТПУ равно сумме времени расчета γ j в табличных вычислителях - tТВ, времени получения разрядов полиадического кода в преобразователе 4 - tМП и времени суммирования (N-1) чисел в сумматоре 6 - tΣ . Время получения γ j в табличных вычислителях примерно равно времени переключения логического элемента: tTB ≈ 10-10C. Оценки времени tМП и tΣ , полученные в [4, с.8-11, 5, с.40-44], описываются формулами
tΣ ≈ (N+3)T+10-11, C;
tМП=TN+(N-1)·3T+2N·τ K, C,
где Т - период частоты генератора гармонического сигнала; τ К - время коммутации управляемых фазовращателей.
Например, при N=6 и Т=τ К=10-11C получаем
ТПР=10-9(3+2)=5·10-9С.
ТПУ=tТВ+τ МВ+tΣ =5,3·10-10C.
Пример: Пусть N=3; m1=5; m2=7; m3=3. Тогда ρ 1,3=2; ρ l,2=3; ρ 2,3=5; d2=6.
Найдем результат деления числа А=47=(2,5,2) на m3=3.
В табличных вычислителях 3.1 и 3.2 по формуле (1) определяются
γ 1=(ρ 1,3(α 1-(α 2)modm1))modm1=(2·(2-2))mod5=0;
γ 2=(ρ 2,3(α 2-(α 3)modm2))modm2=(5·(5-2))mod7=1.
Данные числа поступают соответственно на выходы 7.1 и 7.2 устройства и на входы 1 и 2 преобразователя 4. В этом преобразователе β 1=γ 1=0, а β 2 рассчитывается по формуле (4)

В устройствах отображения 5.1 и 5.2 осуществляется преобразование β 1 → (β 1)mod3=0 и β 2 → (β 2·5)mod3=0. Данные числа складываются в сумматоре 6:
γ 3=(0+0)mod3=0.
Результат сложения поступает на выход 7.3 устройства.
Таким образом, модулярный код частного (А-α N)/mN=(0,1,0).
Проверка. (47-2)/3=15=(0,1,0).
Источники информации
1. Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968. 440 с.
2. Долгов А.И. Диагностика устройств, функционирующих в системе остаточных классов. - М.: Радио и связь, 1982, 64 с.
3. Акаев А.А., Майоров С.А. Оптические методы обработки информации. - М.: Высш. шк., 1988. - 273 с.
4. Овчаренко Л.А. Вариант реализации основных операций в модулярном арифметическом устройстве. - Телекоммуникации, 2001. №3, 8-11 с.
5. Овчаренко Л.А. Когерентный преобразователь модулярного кода.// Телекоммуникации, 2001, №6, 40-44 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ МАСШТАБИРОВАНИЯ ЧИСЛА В МОДУЛЯРНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 2002 |
|
RU2246753C2 |
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ ЧИСЛА В МОДУЛЯРНОМ КОДЕ НА ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ | 2002 |
|
RU2237274C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ И ИСПРАВЛЕНИЯ ОШИБОК В ИЗБЫТОЧНОМ МОДУЛЯРНОМ КОДЕ | 1991 |
|
RU2015620C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЗИЦИОННУЮ СИСТЕМУ СЧИСЛЕНИЯ | 2004 |
|
RU2275741C2 |
| СИНТЕЗАТОР ЧАСТОТЫ | 2002 |
|
RU2237972C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ЭВМ | 2014 |
|
RU2547232C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| ЦИФРОАНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ | 2020 |
|
RU2744475C1 |
| Устройство для сложения и вычитания чисел с плавающей запятой | 1986 |
|
SU1411742A1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
Изобретение относится к области автоматики и вычислительной техники и может быть использовано в вычислительных структурах, функционирующих в модулярной системе счисления (МСС). Техническим результатом является повышение быстродействия выполнения операции деления числа в модулярном коде на одно из основании МСС. Технический результат достигается за счет того, что устройство содержит регистр модулярного кода числа (N - число оснований МСС), преобразователь модулярного кода в полиадический код, (N-1) устройство отображения и сумматор (N-1) чисел по модулю mN (mN - N-ое основание модулярной системы счисления, на которое производится деление). 3 ил.
Устройство для деления числа в модулярном коде на основание системы счисления, содержащее регистр модулярного кода числа, N входов которого являются входами устройства (N - число оснований модулярной системы счисления МСС), отличающееся тем, что в него введены (N-1) табличных вычислителей, преобразователь модулярного кода в полиадический код, (N-1) устройств отображения и сумматор (N-1) чисел по модулю mN (mN - основание, на которое осуществляется деление числа в МСС), причем i-ый выход регистра модулярного кода числа 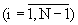 соединен с первым входом i-го табличного вычислителя, ко второму входу которого подключен N-ый выход регистра модуляторного кода числа, выход i-го табличного вычислителя является i-ым выходом устройства и соединен с i-ым входом преобразователя модулярного кода в полиадический код, i-ый выход которого через i-ое устройство отображения соединен с i-ым входом сумматора (N-1) чисел по модулю mN, выход которого является N-ым выходом устройства.
соединен с первым входом i-го табличного вычислителя, ко второму входу которого подключен N-ый выход регистра модуляторного кода числа, выход i-го табличного вычислителя является i-ым выходом устройства и соединен с i-ым входом преобразователя модулярного кода в полиадический код, i-ый выход которого через i-ое устройство отображения соединен с i-ым входом сумматора (N-1) чисел по модулю mN, выход которого является N-ым выходом устройства.
| Устройство для масштабирования чисел | 1989 |
|
SU1667066A1 |
| Устройство для деления чисел | 1989 |
|
SU1683013A1 |
| RU 98110396 А, 20.04.2000 | |||
| US 5349551 А, 20.09.1994 | |||
| ЕР 0601907 А3, 15.06.1994 | |||
| АКУШСКИЙ И.Я | |||
| и др | |||
| Машинная арифметика в остаточных классах | |||
| - М.: Сов | |||
| Радио, 1968, с.12-13, 146-147 | |||
| ДОЛГОВ А.И | |||
| Диагностика устройств, функционирующих в системе остаточных классов | |||
| - М.: Радио и связь, 1982, с.21-22. | |||
Авторы
Даты
2004-06-27—Публикация
2002-09-12—Подача