Изобретение относится к вычислительной технике, предназначено для масштабирования результата произведения целых чисел, представленных в модулярном коде, и может быть использовано в цифровых вычислительных устройствах.
Известно устройство (аналог) (авт. св. СССР №1667066А1, МКИ G 06 F 7/72, Б.И. №28, 1991 г.), содержащее блок элементов задержки, блок вычисления интервального индекса числа, элемент задержки, первый и второй регистры сдвига, регистр модулярного кода числа, регистр интервального индекса, первый и второй блоки мультиплексоров, первый и второй блоки хранения констант, блок управления, первый и второй блоки элементов ИЛИ.
Недостатком данного устройства является низкое быстродействие.
Наиболее близкими по технической сущности (прототипом к предлагаемому изобретению) является устройство (авт. св. СССР №1140114, МКИ G 06 F 7/ 72, Б.И. №6, 1985 г.), содержащее входной и выходной регистр, блоки хранения констант, блоки суммирования вычетов по вспомогательному модулю, элемент задержки, дополнительный блок суммирования, две группы вспомогательных регистров, схему сравнения, реверсивный счетчик и сумматоры коррекции.
Недостаток прототипа - низкая скорость выполнения операции масштабирования в модулярной системе счисления (МСС) вследствие большого количества тактов, в ходе которых реализуется данная операция, и конечного времени переключения полупроводниковых логических вентилей, составляющих основу прототипа.
Задача, на решение которой направлено заявляемое устройство, состоит в повышении производительности перспективных образцов вычислительной техники.
Технический результат выражается в повышении быстродействия (уменьшении временных затрат) выполнения операции масштабирования в модулярной системе счисления.
Технический результат достигается тем, что в устройство, содержащее входной регистр, N входов первого и N входов второго операндов которого являются входами устройства (N - число оснований МСС), введены N блоков вычисления остатков, выходы которых являются выходами устройства, причем i-ый выход k-го операнда  входного регистра соединен с i-ми входами k-ых операндов блоков вычисления остатков, при этом n-ый блок вычисления остатка
входного регистра соединен с i-ми входами k-ых операндов блоков вычисления остатков, при этом n-ый блок вычисления остатка  содержит N устройств вычисления остатка по n-ому основанию и сумматор 3N чисел по модулю mn (mn - n-ое основание МСС,
содержит N устройств вычисления остатка по n-ому основанию и сумматор 3N чисел по модулю mn (mn - n-ое основание МСС, 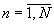 ), причем j-ое устройство вычисления остатка по n-ому основанию (
), причем j-ое устройство вычисления остатка по n-ому основанию (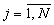 j≠ n) содержит пять табличных вычислителей, при этом n-ый вход первого операнда соединен с первым входом первого и второго табличных вычислителей, а n-ый вход второго операнда - с первым входом третьего и четвертого табличного вычислителя, j-ый вход первого операнда - со вторым входом первого табличного вычислителя и первым входом пятого табличного вычислителя, j-ый вход второго операнда - со вторым входом второго и третьего табличного вычислителя, выходы первого и третьего табличных вычислителей подключены соответственно ко вторым входам четвертого и пятого табличных вычислителей, выход четвертого табличного вычислителя является первым выходом j-го устройства вычисления остатка по n-ому основанию, выход второго табличного вычислителя - вторым выходом j-го устройства вычисления остатка по n-ому основанию, а выход пятого табличного вычислителя - третьим выходом j-го устройства вычисления остатка по n-ому основанию, при этом n-ое устройство вычисления остатка по n-ому основанию содержит три вычислительных блока и два блока умножения, причем i-ые входы
j≠ n) содержит пять табличных вычислителей, при этом n-ый вход первого операнда соединен с первым входом первого и второго табличных вычислителей, а n-ый вход второго операнда - с первым входом третьего и четвертого табличного вычислителя, j-ый вход первого операнда - со вторым входом первого табличного вычислителя и первым входом пятого табличного вычислителя, j-ый вход второго операнда - со вторым входом второго и третьего табличного вычислителя, выходы первого и третьего табличных вычислителей подключены соответственно ко вторым входам четвертого и пятого табличных вычислителей, выход четвертого табличного вычислителя является первым выходом j-го устройства вычисления остатка по n-ому основанию, выход второго табличного вычислителя - вторым выходом j-го устройства вычисления остатка по n-ому основанию, а выход пятого табличного вычислителя - третьим выходом j-го устройства вычисления остатка по n-ому основанию, при этом n-ое устройство вычисления остатка по n-ому основанию содержит три вычислительных блока и два блока умножения, причем i-ые входы 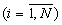 первого и второго операндов подключены соответственно к i-ым входам
первого и второго операндов подключены соответственно к i-ым входам 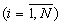 первого и второго вычислительного блока, выходы которых соединены соответственно с первыми входами первого и второго блоков умножения, ко вторым входам которых подключены n-ые входы второго и первого операндов соответственно, а ко входам третьего вычислительного блока подсоединены n-ые входы первого и второго операндов, причем выходы первого и второго блоков умножения и выход третьего вычислительного блока являются соответственно первым, вторым и третьим выходом n-го устройства вычисления остатка по n-ому основанию, при этом выходы устройств вычисления остатков подключены ко входам сумматора 3N чисел по модулю mn, выход которого является выходом n-го блока вычисления остатка.
первого и второго вычислительного блока, выходы которых соединены соответственно с первыми входами первого и второго блоков умножения, ко вторым входам которых подключены n-ые входы второго и первого операндов соответственно, а ко входам третьего вычислительного блока подсоединены n-ые входы первого и второго операндов, причем выходы первого и второго блоков умножения и выход третьего вычислительного блока являются соответственно первым, вторым и третьим выходом n-го устройства вычисления остатка по n-ому основанию, при этом выходы устройств вычисления остатков подключены ко входам сумматора 3N чисел по модулю mn, выход которого является выходом n-го блока вычисления остатка.
Сущность изобретения заключается в получении остатков произведения целого числа А и рационального числа b, представленного в виде дроби 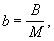 где В - целое число.
где В - целое число.
При этом считается, что числа А и В представлены модулярными кодами: А=(α 1, α 2,... , α N), В=(β 1, β 2,... , β n); α i=A mod mi; β i=В mod mi; mi - совокупность взаимно простых целых чисел; 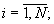 М - диапазон представления чисел в МСС
М - диапазон представления чисел в МСС 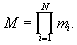
В основу функционирования предлагаемого устройства положены следующие принципы. На основании теоремы о делении на произведение взаимно простых целых чисел [1, с.145] произведение произвольного целого числа А на произвольное рациональное число 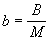 может быть представлено в виде суммы
может быть представлено в виде суммы
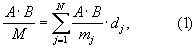
в которой целые числа dj определяются как решение уравнения:
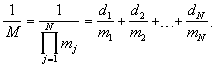
В МСС все переменные, а также результаты арифметических операций должны быть целочисленными [1, с.12]. Поэтому результат масштабирования (1) необходимо привести к целому числу путем округления частного. С этой целью представим сумму в (1) в следующей эквивалентной форме:
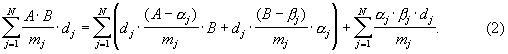
Отметим, что выражения под знаком первой суммы в правой части формулы (2) всегда приводят к целым числам. Тогда округленное значение частного (1) может быть вычислено с помощью приближенного соотношения:
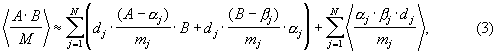
где  - символ округления до ближайшего целого числа.
- символ округления до ближайшего целого числа.
Численный расчет (3) для 0≤ А<М и 0≤ В<М показывает, что в 67% случаев получается точный результат, а в 33% - отличается на ± 1. То есть это не хуже, чем в аналогичных арифметических устройствах, функционирующих в позиционной системе счисления.
Из выражения (3) видно, что для нахождения модулярного кода частного 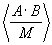 необходимо вычислить остатки входящих в его состав слагаемых по основаниям
необходимо вычислить остатки входящих в его состав слагаемых по основаниям 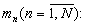
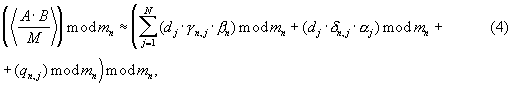
где 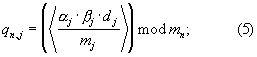
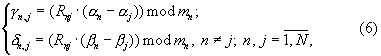
Rnj определяется из решения сравнения (Rnj·mj)mod mn≡ 1.
Для нахождения остатков γ n,n и δ n,n может быть применен подход, изложенный в [2, с.8-9].
Согласно этому подходу учтем, что для 0≤ А<М и 0≤ В<М всегда справедливы неравенства:
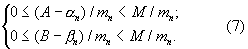
Так как единственным условием при выборе МСС является взаимная простота ее оснований [1, с.13], то нумерация этих оснований может быть произвольной. Соответственно при определении остатков частных 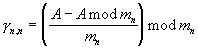 и
и 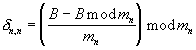 основания
основания 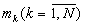 могут перенумеровываться таким образом, чтобы основанию mn соответствовал номер N в новой системе:
могут перенумеровываться таким образом, чтобы основанию mn соответствовал номер N в новой системе: 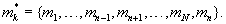 Тогда в полиадическом коде частных
Тогда в полиадическом коде частных 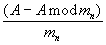 и
и 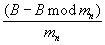 старший разряд кода будет равен нулю, а остатки γ n,n и δ n,n могут быть вычислены по формулам [2, с.8]:
старший разряд кода будет равен нулю, а остатки γ n,n и δ n,n могут быть вычислены по формулам [2, с.8]:
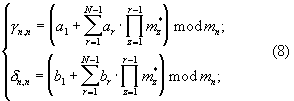
где ar и br - r-ый разряд полиадического кода частных 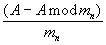 и
и 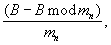 определяемый в соответствии с [3, с.21-22] выражениями:
определяемый в соответствии с [3, с.21-22] выражениями:
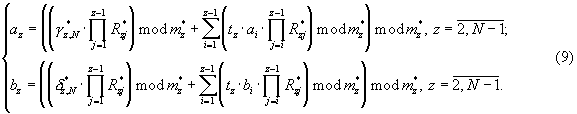
Здесь  находится из решения сравнения
находится из решения сравнения 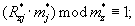
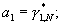
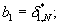
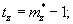
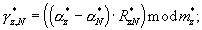
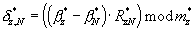

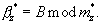
Таким образом, алгоритм расчета модулярного кода частного 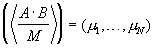 состоит в получении для всех n
состоит в получении для всех n 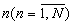 остатков
остатков 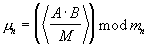 по формуле (4).
по формуле (4).
Для расчета этих остатков вычисляются 3N значений qn,j, γ n,j и δ n,j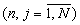 по формулам (5), (6) и (8), которые затем суммируются по модулю mn.
по формулам (5), (6) и (8), которые затем суммируются по модулю mn.
Значения γ n,j и δ n,j (n, 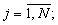 n≠ j), а также qn,j
n≠ j), а также qn,j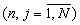 могут быть определены в табличных вычислителях, подобных описанным в [3, с.16-17]. Такой табличный вычислитель, содержащий mn·mj двухвходовых элементов "И", представляет собой матричный дешифратор, на вход которого поступают два операнда в унитарном коде. Элементы "И" находятся в местах пересечения шин данных операндов в унитарном коде, соответствующих результату двухместной операции (5) или (6), а выходы элементов "И" объединяются в соответствующих элементах "ИЛИ", число которых равно mn. Поскольку логический сигнал в таком табличном вычислителе распространяется через два логических элемента, время вычисления qn,j, γ n,j и δ n,j будет равно
могут быть определены в табличных вычислителях, подобных описанным в [3, с.16-17]. Такой табличный вычислитель, содержащий mn·mj двухвходовых элементов "И", представляет собой матричный дешифратор, на вход которого поступают два операнда в унитарном коде. Элементы "И" находятся в местах пересечения шин данных операндов в унитарном коде, соответствующих результату двухместной операции (5) или (6), а выходы элементов "И" объединяются в соответствующих элементах "ИЛИ", число которых равно mn. Поскольку логический сигнал в таком табличном вычислителе распространяется через два логических элемента, время вычисления qn,j, γ n,j и δ n,j будет равно
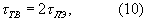
где τ ЛЭ - время задержки в логическом элементе.
Для сложения 3N чисел по модулю mn может быть применен сумматор, описанный в [патент РФ №2188448, МПК G 06 F 7/72, Б.И. №24, 2002 г.], который содержит управляемые фазовращатели, генератор гармонического сигнала, фазовращатели на фиксированное значение фазы и измеритель фазы гармонического сигнала. Время сложения 3N чисел в таком сумматоре будет равно
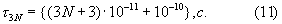
При выводе формулы (11) полагалось, что частота генератора гармонического сигнала равна 100 ГГц, а время принятия решения о значении модульной операции -10-10 с.
Для получения разрядов полиадического кода ar и br (9) может быть применено устройство для преобразования чисел из кода системы остаточных классов в полиадический код, описанное в [патент РФ №2187886, МПК Н 03 М 7/18, Б.И. №23, 2002 г.], которое содержит входные регистры, генератор гармонического сигнала, управляемые фазовращатели и измерители фазы гармонического сигнала. Время получения разрядов полиадического кода в таком преобразователе будет равно
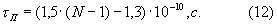
При выводе формулы (12) полагалось, что частота генератора гармонического сигнала равна 100 ГГц, время принятия решения о значении модульной операции -10-10 с, а время коммутации управляемых фазовращателей -10-11 c.
Получение остатков γ n,n и γ n,n может быть осуществлено в вычислительном блоке, содержащем табличные вычислители значений γ n,j и δ n,j (n,  n≠ j) (6), устройство для преобразования чисел из кода системы остаточных классов в полиадический код, устройства отображения, осуществляющие унарные преобразования
n≠ j) (6), устройство для преобразования чисел из кода системы остаточных классов в полиадический код, устройства отображения, осуществляющие унарные преобразования 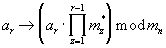
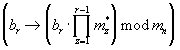 и сумматор N-1 чисел по модулю mn. Структурная схема такого вычислительного блока приведена в [2, с.8, рис.1]. Полученная в [2, с. 10] оценка времени расчета остатков γ n,n и δ n,n составляет 3· 10-9 с.
и сумматор N-1 чисел по модулю mn. Структурная схема такого вычислительного блока приведена в [2, с.8, рис.1]. Полученная в [2, с. 10] оценка времени расчета остатков γ n,n и δ n,n составляет 3· 10-9 с.
Сравним быстродействие прототипа и предлагаемого устройства
В прототипе время получения результата масштабирования равно
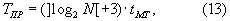
где ][ - символ округления в большую сторону; tМТ - длительность модульного такта устройства.
При оценке значения tМТ учтем, что основные функциональные элементы прототипа (регистры, сумматоры, счетчики и т.п.) содержат от 10 до 50 и более логических элементов. Соответственно время задержки логического сигнала в этих функциональных элементах может достигать более 50τ ЛЭ. Поскольку tМТ не может быть меньше наибольшего времени задержки логического сигнала в функциональных элементах прототипа, то примем
tмт≈ 50τ ЛЭ.
Тогда
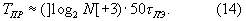
Будем считать, что минимальное время задержки в логическом элементе составляет τ ЛЭ≈ 10-10 с [4, с.173].
В предлагаемом устройстве время вычисления ТПУ остатка результата округления частного 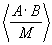 по основанию mn
по основанию mn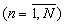 складывается из времени определения остатков γ n,n(δ n,n)-3· 10-9 с, времени расчета остатков γ n,j, δ n,j
складывается из времени определения остатков γ n,n(δ n,n)-3· 10-9 с, времени расчета остатков γ n,j, δ n,j и qn,j
и qn,j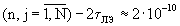 с и времени суммирования 3N чисел - τ 3N={(3N+3)· 10-11+10-10}, с.
с и времени суммирования 3N чисел - τ 3N={(3N+3)· 10-11+10-10}, с.
Например, при N=6 получаем
ТПР=50· 10-10·(3+3)=30· 10-9 с=30 нс;
TПУ=3· 10-9+2· 10-10+(18+3)· 10-11+10-10≈ 3,5 нс.
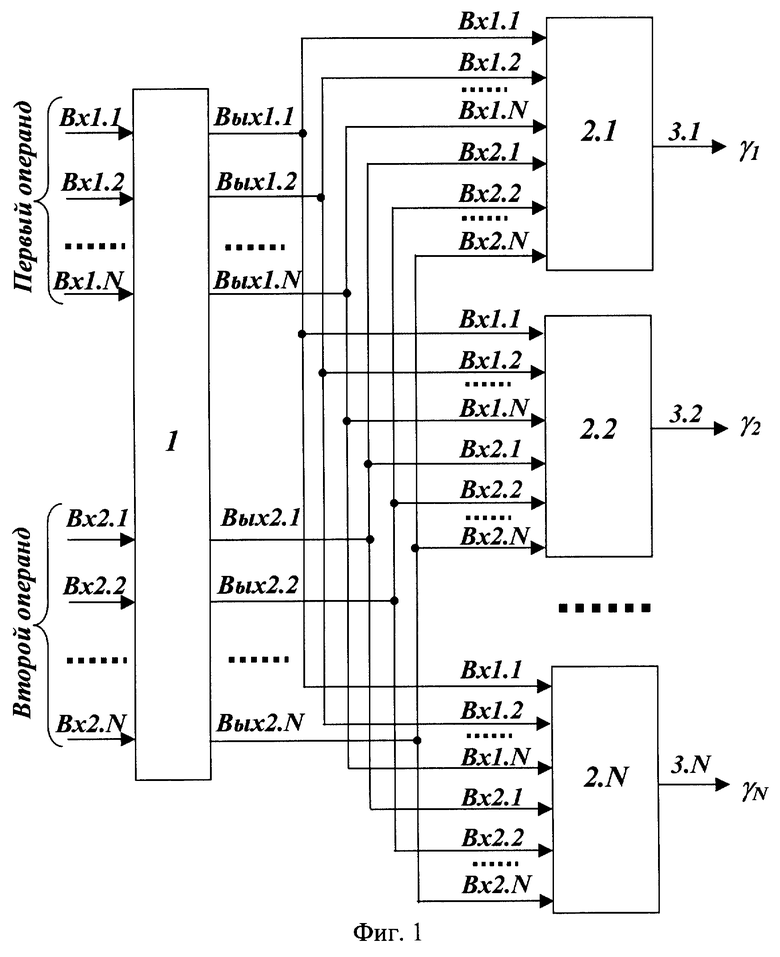
Структурная схема устройства для масштабирования числа в модулярной системе счисления представлена на фиг.1.
В данной схеме Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N (N - число оснований МСС) - входы первого (А) и второго (В) операндов, соответственно 1 - входной регистр, 2.1-2.N - блоки вычисления остатков, 3.1-3.N - выходы устройства.
Входы операндов А и В соединены с информационными входами Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N входного регистра 1 соответственно. Выходы Вых 1.1-Вых 1.N и Вых 2.1-Вых 2.N входного регистра 1 подключены ко входам Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N блоков вычисления остатков 2.1-2.N, выходы которых подключены к соответствующим выходам устройства 3.1-3.N.
Реализация основных узлов устройства для масштабирования числа в модулярной системе счисления приведена на фиг.2-5.
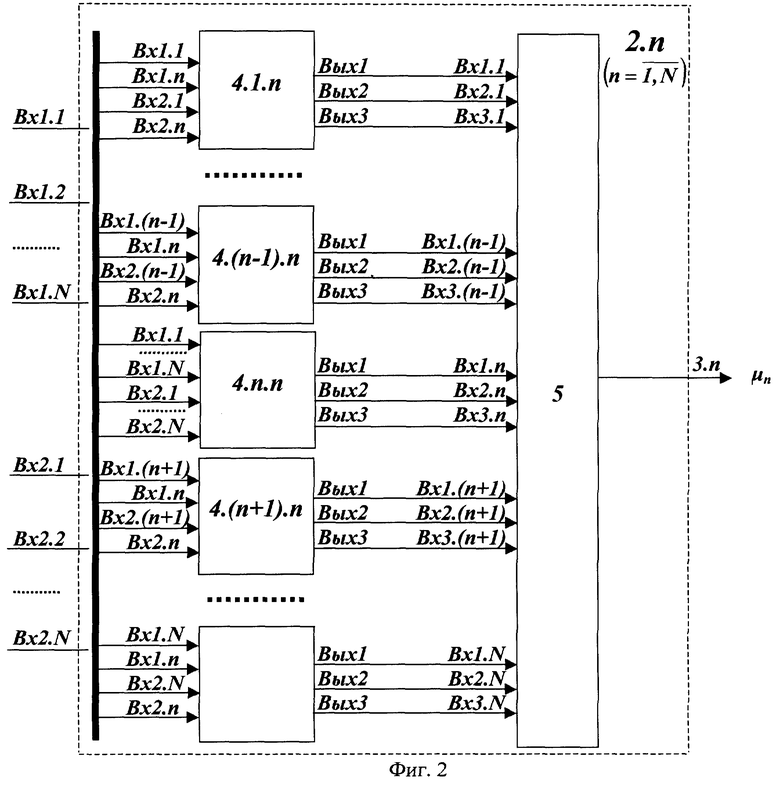
На фиг.2 представлена структурная схема n-ого блока вычисления остатка 2.n, 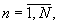 где Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N - входы блока вычисления остатка, 4.1.n-4.N.n - устройства вычисления остатка по n-ому основанию, 5 - сумматор 3N чисел по модулю mn, 3.n - выход n-го блока вычисления остатка.
где Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N - входы блока вычисления остатка, 4.1.n-4.N.n - устройства вычисления остатка по n-ому основанию, 5 - сумматор 3N чисел по модулю mn, 3.n - выход n-го блока вычисления остатка.
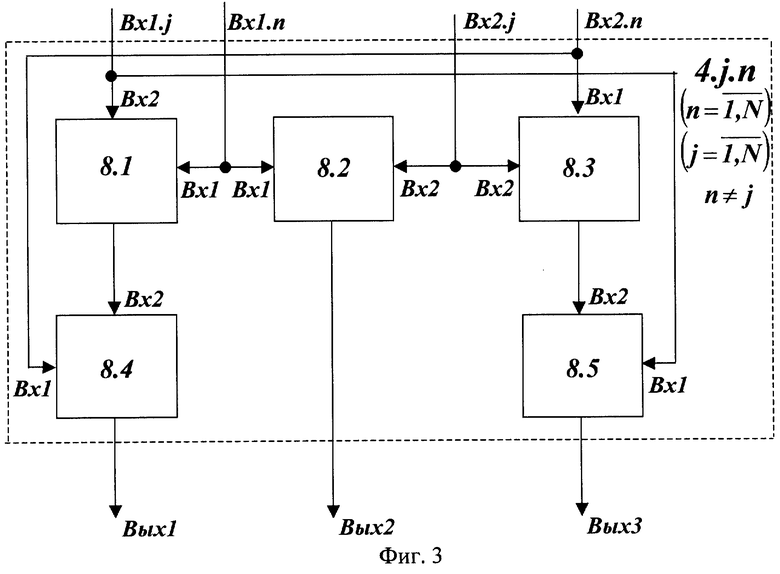
На фиг.3 представлена структурная схема j-го устройства вычисления остатка по n-ому основанию 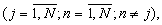 где Вх 1.n, Вх 2.n, Вх 1.j и Вх 2.j - входы устройства, 8.1-8.5 - табличные вычислители, Вых 1-Вых 3 - выходы устройства вычисления остатка по n-ому основанию.
где Вх 1.n, Вх 2.n, Вх 1.j и Вх 2.j - входы устройства, 8.1-8.5 - табличные вычислители, Вых 1-Вых 3 - выходы устройства вычисления остатка по n-ому основанию.
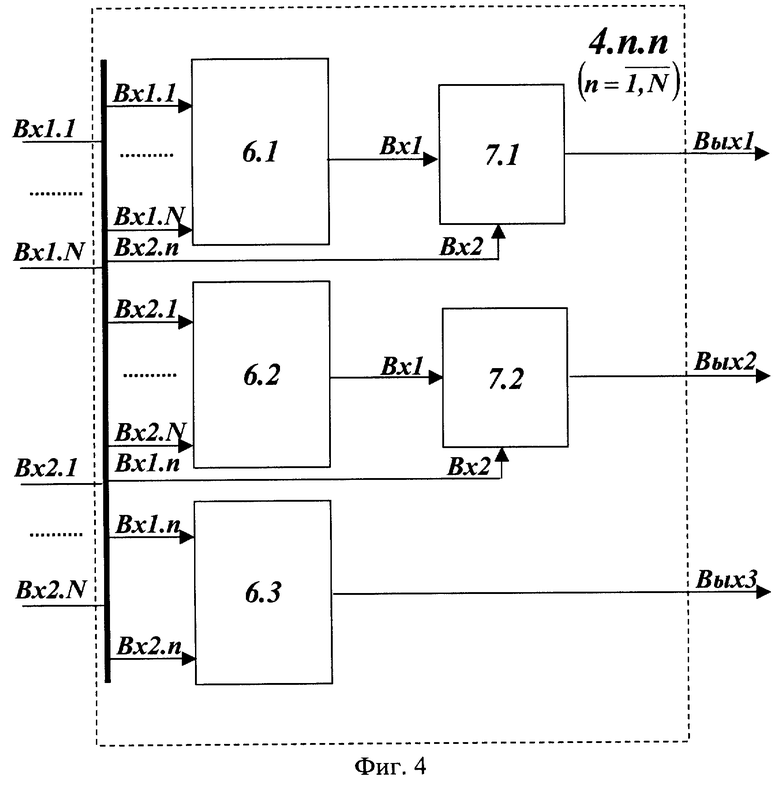
На фиг.4 представлена структурная схема n-го устройства вычисления остатка по n-ому основанию, где Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N -входы устройства, 6.1-6.3 - вычислительные блоки, 7.1-7.2 - блоки умножения, Вых 1-Вых 3 - выходы n-го устройства вычисления остатка по n-ому основанию.
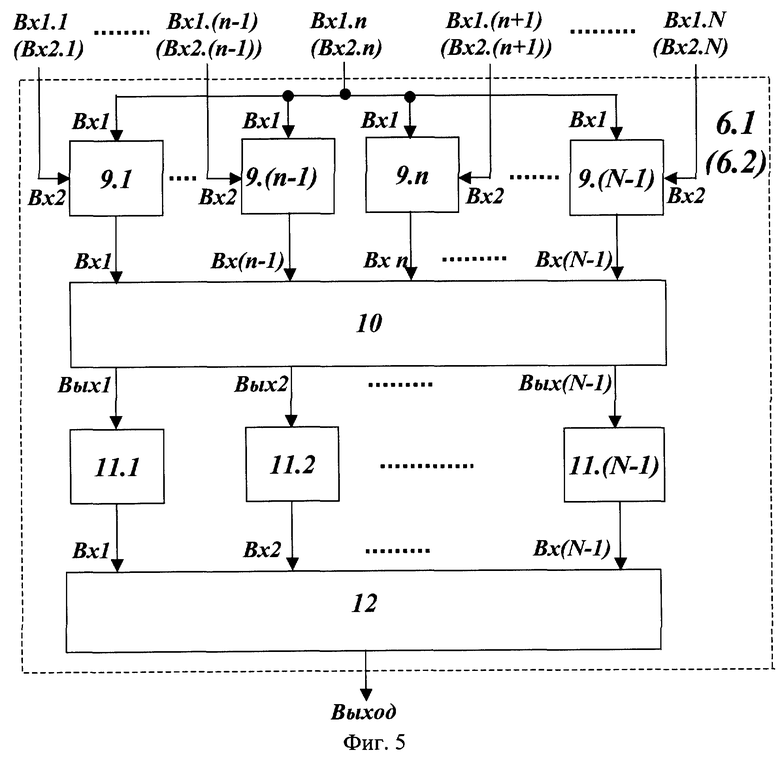
На фиг.5 представлена структурная схема вычислительного блока 6.1 (6.2). В данной схеме Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N - входы вычислительного блока, 9.1-9.(N-1) - табличные вычислители, 10 - устройство для преобразования чисел из кода системы остаточных классов в полиадический код, 11.1-11.(N-1) - устройства отображения, 12 - сумматор (N-1) чисел по модулю mn.
Рассмотрим работу устройства.
Остатки (α 1, α 2,... ,α N) операнда А и остатки (β 1, β 2,... ,β N) операнда В в МСС подаются на информационные входы Вх 1.1-Вх 1.N и Вх 2.1-Вх 2.N соответственно и записываются во входной регистр 1. С выходов Вых 1.1-Вых 1.N и Вых 2.1-Вых 2.N входного регистра остатки α j и β j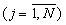 в унитарном коде поступают на соответствующие входы блоков вычисления остатков 2.1.-2.N.
в унитарном коде поступают на соответствующие входы блоков вычисления остатков 2.1.-2.N.
В j-ом устройстве вычисления остатка по n-ому основанию 4.j.n 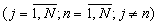 остаток α j (со входа Вх 1.j) поступает на Вх 1 табличного вычислителя 8.5 и Вх 2 табличного вычислителя 8.1, остаток α n (со входа Вх 1.n) - на Вх 1 табличных вычислителей 8.1 и 8.2, остаток β j (со входа Вх 2.j) - на Вх 2 табличных вычислителей 8.2 и 8.3, а остаток β n (со входа Вх 2.n) - на Вх 1 табличных вычислителей 8.3 и 8.4.
остаток α j (со входа Вх 1.j) поступает на Вх 1 табличного вычислителя 8.5 и Вх 2 табличного вычислителя 8.1, остаток α n (со входа Вх 1.n) - на Вх 1 табличных вычислителей 8.1 и 8.2, остаток β j (со входа Вх 2.j) - на Вх 2 табличных вычислителей 8.2 и 8.3, а остаток β n (со входа Вх 2.n) - на Вх 1 табличных вычислителей 8.3 и 8.4.
В табличных вычислителях 8.1 и 8.3 по формуле (6) соответственно рассчитываются остатки γ n,j и δ n,j, а в табличном вычислителе 8.2 по формуле (5) вычисляется остаток qn,j, который поступает на Вых 2 устройства вычисления остатка 4.j.n.
Затем в табличных вычислителях 8.4 и 8.5 соответственно вычисляются слагаемые формулы (4): (dj·γ n,j·β n)mod mn и (dj·δ n,j·α j)mod mn, которые поступают на Вых 1 и Вых 3 устройства вычисления остатка 4.j.n.
В n-ом устройстве вычисления остатка по n-ому основанию 4.n.n 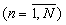 остатки α i
остатки α i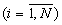 (со входов Вх 1.i) поступают на Вх 1.i вычислительного блока 6.1, остатки β i
(со входов Вх 1.i) поступают на Вх 1.i вычислительного блока 6.1, остатки β i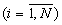 (со входов Вх 2.i) поступают на Вх 2.i вычислительного блока 6.2, а остатки α n и β n (со входов Вх 1.n и Вх 2.n) - на Вх 1.n и Вх 2.n вычислительного блока 6.3. В вычислительном блоке 6.3 по формуле (5) рассчитывается остаток qn,n, который поступает на Вых 3 устройства вычисления остатка 4.n.n.
(со входов Вх 2.i) поступают на Вх 2.i вычислительного блока 6.2, а остатки α n и β n (со входов Вх 1.n и Вх 2.n) - на Вх 1.n и Вх 2.n вычислительного блока 6.3. В вычислительном блоке 6.3 по формуле (5) рассчитывается остаток qn,n, который поступает на Вых 3 устройства вычисления остатка 4.n.n.
В вычислительном блоке 6.1 остатки α i (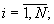 i≠ n) со входов Вх 1.i поступают на Вх 2 табличных вычислителей 9.1 (при i<n) и 9.(i-1) (при i>n), а на Вх 1 этих табличных вычислителей поступает остаток α n со входа Вх 1.n вычислительного блока.
i≠ n) со входов Вх 1.i поступают на Вх 2 табличных вычислителей 9.1 (при i<n) и 9.(i-1) (при i>n), а на Вх 1 этих табличных вычислителей поступает остаток α n со входа Вх 1.n вычислительного блока.
Учитывая то, что в вычислительном блоке 6.1 основания mk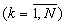 перенумерованы следующим образом:
перенумерованы следующим образом:  в табличных вычислителях 9.1-9.(N-1) вычисляются остатки
в табличных вычислителях 9.1-9.(N-1) вычисляются остатки 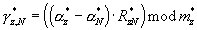
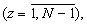 где остаток
где остаток 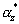 равен остатку α i в исходной системе оснований, номер которого - i соответствует номеру z в новой системе оснований.
равен остатку α i в исходной системе оснований, номер которого - i соответствует номеру z в новой системе оснований.
С выходов табличных вычислителей 9.1-9.(N-1) остатки 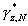 поступают на вход устройства преобразования чисел из кода системы остаточных классов в полиадический код - 10, где по формуле (9) вычисляются разряды ar
поступают на вход устройства преобразования чисел из кода системы остаточных классов в полиадический код - 10, где по формуле (9) вычисляются разряды ar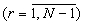 полиадического кода. Данные разряды с Вых 1-Вых (N-1) устройства преобразования 10 поступают на входы устройств отображения 11.1-11.(N-1), где соответственно осуществляются унарные преобразования
полиадического кода. Данные разряды с Вых 1-Вых (N-1) устройства преобразования 10 поступают на входы устройств отображения 11.1-11.(N-1), где соответственно осуществляются унарные преобразования 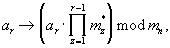 а в сумматоре (N-1) чисел по модулю mn 12 в соответствии с формулой (8) получается остаток γ n,n.
а в сумматоре (N-1) чисел по модулю mn 12 в соответствии с формулой (8) получается остаток γ n,n.
Аналогичным образом при замене α i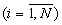 на β i в вычислительном блоке 6.2 рассчитывается остаток δ n,n.
на β i в вычислительном блоке 6.2 рассчитывается остаток δ n,n.
С выходов сумматоров 12 вычислительных блоков 6.1 и 6.2 остатки γ n,n и δ n,n поступают на Вх 1 первого (7.7) и второго (7.2) блоков умножения, на Вх 2 которых поступают соответственно остатки β n (со входа Вх 2.n) и α n (со входа Вх 1.n). В блоках умножения 7.1 и 7.2 соответственно получаются слагаемые формулы (4): (dn·γ n,n·β n)mod mn и (dn·δ n,n·α n)mod mn, которые поступают на Вых 1 и Вых 2 устройства вычисления остатка 4.n.n.
Данные с Вых 1-Вых 3 j-ого устройства вычисления остатка по n-ому основанию 4.j.n 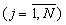 поступают соответственно Вх 1.j-Вх 3.j сумматора 3N чисел по модулю mn, где по формуле (4) вычисляется остаток результата масштабирования
поступают соответственно Вх 1.j-Вх 3.j сумматора 3N чисел по модулю mn, где по формуле (4) вычисляется остаток результата масштабирования 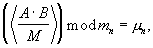 который поступает на выход 3.n устройства для масштабирования числа в МСС.
который поступает на выход 3.n устройства для масштабирования числа в МСС.
Пример: Пусть заданы основания модулярной системы счисления: m1=3, m2=5, m3=7, m4=11 (N=4), в которой числа А=100 и В=578 представлены кодами: А=(1, 0, 2, 1); В=(2, 3, 4, 6). Диапазон представления чисел в такой МСС: 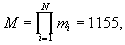 а коэффициенты в формуле (4) принимают следующие значения: d1=1, d2=-4, d3=2, d4=2. Требуется найти модулярный код результата масштабирования частного
а коэффициенты в формуле (4) принимают следующие значения: d1=1, d2=-4, d3=2, d4=2. Требуется найти модулярный код результата масштабирования частного 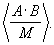
Рассмотрим работу предлагаемого устройства для приведенных выше исходных данных.
Коды операнда А=(1, 0, 2, 1) и операнда В=(2, 3, 4, 6) поступают на соответствующие входы Вх 1.1-Вх 1.4 и Вх 2.1-Вх 2.4 входного регистра 1. С выходов Вых 1.1-Вых 1.4 и Вых 2.1-Вых 2.4 входного регистра 1 операнды А и В поступают на соответствующие входы Вх 1.1-Вх 1.4 и Вх 2.1-Вх 2.4 блоков вычисления остатков 2.1-2.4.
Проиллюстрируем порядок вычисления остатка результата масштабирования на примере расчета остатка по первому основанию (m1=3) в блоке вычисления остатка 2.1.
Коды операндов А и В со входов Вх 1.1-Вх 1.4 и Вх 2.1-Вх 2.4 блока вычисления остатка 2.1 поступают соответственно на входы Вх 1.1-Вх 1.4 и Вх 2.1-Вх 2.4 устройства вычисления остатка 4.1.1. При этом остатки α 1 (со входа Вх 1.1) и β 1 (со входа Вх 2.1) подаются на Вх 1.1 и Вх 2.1 устройств вычисления остатка 4.2.1-4.4.1. На Вх 1.j и Вх 2.j устройств вычисления остатка 4.j.1  соответственно поступают остатки α j и β j. В табличных вычислителях 8.2 устройств вычисления остатка 4.2.1-4.4.1 по формуле (5) вычисляются остатки
соответственно поступают остатки α j и β j. В табличных вычислителях 8.2 устройств вычисления остатка 4.2.1-4.4.1 по формуле (5) вычисляются остатки
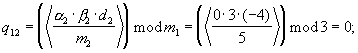
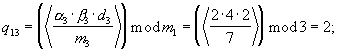
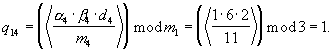
Данные остатки поступают на Вых 2 устройств вычисления остатка 4.2.1-4.4.1.
Одновременно в табличных вычислителях 8.1 и 8.3 устройств вычисления остатка 4.2.1-4.4.1 по формуле (6) определяются остатки γ 1,j и δ 1,j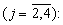
γ 12=(R12·(α 1-α 2))mod m1=(2· (1-0))mod 3=2;
γ 13=(R13·(α 1-α 3))mod m1=(1· (1-2))mod 3=2;
γ 14=(R14·(α 1-α 4))mod m1=(2· (1-1))mod 3=0;
δ 12=(R12·(β 1-β 2))mod m1=(2· (2-3))mod 3=1;
δ 13=(R13·(β 1-β 3))mod m1=(1· (2-4))mod 3=1;
δ 14=(r14·(β 1-β 4))mod m1=(2· (2-6))mod 3=1,
где R12=R14=2; R13=1.
Затем в табличных вычислителях 8.4 и 8.5 устройств вычисления остатка 4.2.1-4.4.1 рассчитываются остатки слагаемых в формуле (4) (dj·γ 1,j·β 1)mod m1 и (dj·δ 1,j·α j)mod m1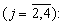
(d2·γ 1,2·β 1)mod m1=((-4)· 2· 2)mod 3=2;
(d3·γ 1,3·β 1)mod m1=(2· 2· 2)mod 3=2;
(d4·γ 1,4·β 1)mod m1=(2· 0· 2)mod 3=0;
(d2·δ 1,2·α 2)mod m1=((-4)· 1· 0)mod 3=0;
(d3·δ 1,3· α 3)mod m1=(2· 1· 2)mod 3=1;
(d4·δ 1,4·α 4)mod m1=(2· 1· 1)mod 3=2.
Далее остаток (dj·γ 1,j·β 1) mod m1 поступает на Вых 1, а остаток (dj·δ 1,j·α j)mod m1 - на Вых 3 устройства вычисления остатка 4.j.1.
В устройстве вычисления остатка 4.1.1 остатки α i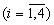 (со входов Вх 1.i) поступают на Вх 1.i вычислительного блока 6.1, остатки β i
(со входов Вх 1.i) поступают на Вх 1.i вычислительного блока 6.1, остатки β i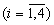 (со входов Вх 2.i) поступают на Вх 2.i вычислительного блока 6.2, а остатки α 1 и β 1 (со входов Вх 1.1 и Вх 2.1) - на Вх 1.1 и Вх 2.1 вычислительного блока 6.3. В вычислительном блоке 6.3 по формуле (5) рассчитывается остаток
(со входов Вх 2.i) поступают на Вх 2.i вычислительного блока 6.2, а остатки α 1 и β 1 (со входов Вх 1.1 и Вх 2.1) - на Вх 1.1 и Вх 2.1 вычислительного блока 6.3. В вычислительном блоке 6.3 по формуле (5) рассчитывается остаток
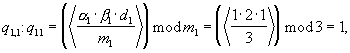
который поступает на Вых 3 устройства вычисления остатка 4.1.1.
В вычислительном блоке 6.1 остатки α i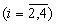 со входов Вх 1.i поступают на Вх 2 табличных вычислителей 9.i, а на Вх 1 этих табличных вычислителей поступает остаток α 1 со входа Вх 1.1 вычислительного блока.
со входов Вх 1.i поступают на Вх 2 табличных вычислителей 9.i, а на Вх 1 этих табличных вычислителей поступает остаток α 1 со входа Вх 1.1 вычислительного блока.
В вычислительном блоке 6.1 основания mk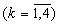 перенумерованы следующим образом:
перенумерованы следующим образом: 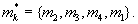 Соответственно в табличных вычислителях 9.1-9.3 вычисляются остатки
Соответственно в табличных вычислителях 9.1-9.3 вычисляются остатки 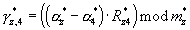
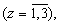 где, как уже отмечалось выше, остаток
где, как уже отмечалось выше, остаток 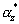 равен остатку α i в исходной системе оснований, номер которого - i соответствует номеру z в новой системе оснований, то есть
равен остатку α i в исходной системе оснований, номер которого - i соответствует номеру z в новой системе оснований, то есть 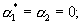
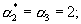
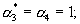 а коэффициенты
а коэффициенты 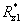 принимают следующие значения:
принимают следующие значения: 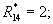
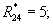
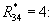
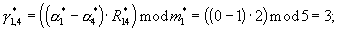
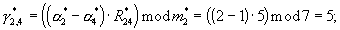
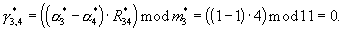
С выходов табличных вычислителей 9.1-9.3 остатки 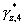 поступают на вход устройства преобразования чисел из кода системы остаточных классов в полиадический код - 10, где по формуле (9) вычисляются разряды аr
поступают на вход устройства преобразования чисел из кода системы остаточных классов в полиадический код - 10, где по формуле (9) вычисляются разряды аr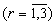 полиадического кода:
полиадического кода:
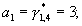

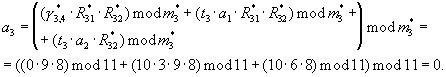
Данные разряды с Вых 1-Вых 3 устройства преобразования 10 поступают на входы устройств отображения 11.1-11.3, где соответственно осуществляются унарные преобразования
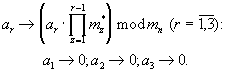
Преобразованные числа в соответствии с формулой (8) складываются в сумматоре 12 трех чисел по модулю 3, где получается остаток γ 1,1=0, который поступает на Вх 1 блока умножения 7.1, а на Вх 2 этого блока умножения подается остаток β 1 (со входа Вх 2.1). В блоке умножения 7.1 рассчитывается слагаемое формулы (4): (d1·γ 1,1·β 1)mod m1=(1· 0· 2)mod 3=0, которое поступает на Вых 1 устройства вычисления остатка 4.1.1.
Аналогичным путем при замене α i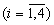 на β i в вычислительном блоке 6.2 рассчитывается остаток δ 1,1:
на β i в вычислительном блоке 6.2 рассчитывается остаток δ 1,1:
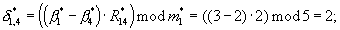
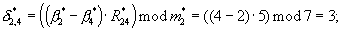
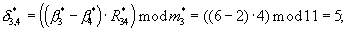
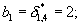
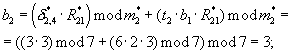
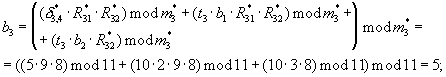
b1→2; b2→0; b3→1; δ 1,1=0;
(d1·δ 1,1·α 1)modm1=(1· 0· 1)mod3=0.
Рассчитанное значение (d1·δ 1,1·α 1)mod m1 подается на Вых 2 устройства вычисления остатка 4.1.1.
И, наконец, полученные данные с Вых 1-Вых 3 устройств вычисления остатков 4.j.n 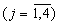 поступают соответственно Вх 1.j-Вх 3.j сумматора двенадцати чисел по модулю 3, где по формуле (4) вычисляется остаток результата масштабирования
поступают соответственно Вх 1.j-Вх 3.j сумматора двенадцати чисел по модулю 3, где по формуле (4) вычисляется остаток результата масштабирования 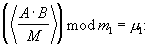
μ 1=(0+2+2+0+0+0+1+2+1+0+2+1)mod 3=2,
который поступает на выход 3.1 устройства для масштабирования числа в МСС.
Аналогичным путем в блоках вычисления остатка 2.2 - 2.4 рассчитываются значения μ 2=0; μ 3=1; μ 4=6.
Таким образом, модулярный код результата масштабирования имеет 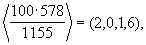 что соответствует числу 50 в позиционном коде.
что соответствует числу 50 в позиционном коде.
Проверка: 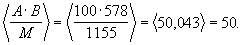
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968. - 440 с.
2. Овчаренко Л.А., Лопатин Д.С. Деление числа в модулярном коде на основание системы счисления.// Телекоммуникации, 2002, №6, с.7-10.
3. Долгов А.И. Диагностика устройств, функционирующих в системе остаточных классов. - М.: Радио и связь, 1982, 64 с.
4. Акаев А.А., Майоров С.А. Оптические методы обработки информации. - М.: Высш. шк., 1988. - 273 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ ЧИСЛА В МОДУЛЯРНОМ КОДЕ НА ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ | 2002 |
|
RU2231822C2 |
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ ЧИСЛА В МОДУЛЯРНОМ КОДЕ НА ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ | 2002 |
|
RU2237274C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ЭВМ | 2014 |
|
RU2547232C1 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ЭВМ | 2011 |
|
RU2458384C1 |
| СИНТЕЗАТОР ЧАСТОТЫ | 2002 |
|
RU2237972C2 |
| ЦИФРОВОЙ СИНТЕЗАТОР ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ | 2003 |
|
RU2239281C2 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
| УСТРОЙСТВО ДЛЯ СЛОЖЕНИЯ И ВЫЧИТАНИЯ ЧИСЕЛ ПО МОДУЛЮ | 1998 |
|
RU2145112C1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПО МОДУЛЮ | 1999 |
|
RU2157560C1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ЧИСЕЛ ПО МОДУЛЮ | 1998 |
|
RU2137181C1 |
Изобретение относится к вычислительной технике, предназначено для масштабирования результата произведения целых чисел, представленных в модулярном коде, и может быть использовано в цифровых вычислительных устройствах. Техническим результатом является повышение быстродействия алгоритма масштабирования результата в модулярной системе счисления (МСС), в котором реализуется операция умножения произвольного целого числа на произвольное рациональное число путем представления рационального числа в виде отношения целых чисел. Технический результат достигается введением N блоков вычисления остатков, каждый из которых содержит N устройств вычисления остатков по основаниям МСС, включающих в свой состав блоки умножения, сумматоры 3N чисел по модулю и табличные вычислители. 5 ил.
Устройство для масштабирования числа в модулярной системе счисления (МСС), содержащее входной регистр, N входов первого и N входов второго операндов которого являются входами устройства (N - число оснований МСС), отличающееся тем, что в него введены N блоков вычисления остатков, выходы которых являются выходами устройства, причем i-й выход k-го операнда (
 ) входного регистра соединен с i-ми входами k-х операндов блоков вычисления остатков, при этом n-й блок вычисления остатка
) входного регистра соединен с i-ми входами k-х операндов блоков вычисления остатков, при этом n-й блок вычисления остатка 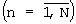 содержит N устройств вычисления остатка по n-му основанию и сумматор 3N чисел по модулю mn (mn - n-е основание МСС,
содержит N устройств вычисления остатка по n-му основанию и сумматор 3N чисел по модулю mn (mn - n-е основание МСС, 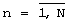 ), причем j-е устройство вычисления остатка по n-му основанию (
), причем j-е устройство вычисления остатка по n-му основанию (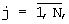 j≠ n) содержит пять табличных вычислителей, причем первый и третий табличные вычислители предназначены для расчета остатков γ n,j и δ n,j, причем γ n,j = (Rnj·(α n-α j))mod mn, δ n,j=(Rnj·(β n-β j))mod mn, Rnj определяется из решения сравнения (Rnj·mj)mod mn≡ 1, α j=A mod mj, α n=A mod mn, β j=В mod mj, β n=B mod mn, А и В - соответственно первый и второй целочисленные операнды, при этом второй табличный вычислитель предназначен для вычисления остатка qn, j, причем
j≠ n) содержит пять табличных вычислителей, причем первый и третий табличные вычислители предназначены для расчета остатков γ n,j и δ n,j, причем γ n,j = (Rnj·(α n-α j))mod mn, δ n,j=(Rnj·(β n-β j))mod mn, Rnj определяется из решения сравнения (Rnj·mj)mod mn≡ 1, α j=A mod mj, α n=A mod mn, β j=В mod mj, β n=B mod mn, А и В - соответственно первый и второй целочисленные операнды, при этом второй табличный вычислитель предназначен для вычисления остатка qn, j, причем 
где 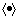 - символ округления до ближайшего целого числа,
- символ округления до ближайшего целого числа,
а целые числа dj определяют как решение уравнения
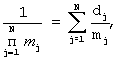
причем четвертый и пятый табличные вычислители предназначены для вычисления значений (dj·γ n,j·β n)mod mn и (dj·δ n,j·α j)mod mn, при этом n-й вход первого операнда соединен с первым входом первого и второго табличных вычислителей, а n-й вход второго операнда - с первым входом третьего и четвертого табличного вычислителя, j-й вход первого операнда - со вторым входом первого табличного вычислителя и первым входом пятого табличного вычислителя, j-й вход второго операнда - со вторыми входами второго и третьего табличных вычислителей, выходы первого и третьего табличных вычислителей подключены соответственно ко вторым входам четвертого и пятого табличных вычислителей, выход четвертого табличного вычислителя является первым выходом j-го устройства вычисления остатка по n-му основанию, выход второго табличного вычислителя - вторым выходом j-го устройства вычисления остатка по n-му основанию, а выход пятого табличного вычислителя - третьим выходом j-го устройства вычисления остатка по n-му основанию, при этом n-е устройство вычисления остатка по n-му основанию содержит три вычислительных блока для вычисления остатков qn,n, γ n,n, δ n, n и два блока умножения, причем
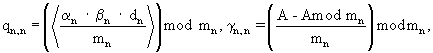

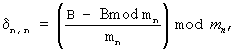
где  - символ округления до ближайшего целого числа, целые числа dn определяются как решение уравнения
- символ округления до ближайшего целого числа, целые числа dn определяются как решение уравнения
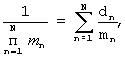
α n=Amod mn,
β n=Bmod mn,

А и В - соответственно первый и второй целочисленные операнды,
причем i-е входы (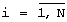 ) первого и второго операндов подключены соответственно к i-м входам (
) первого и второго операндов подключены соответственно к i-м входам (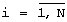 ) первого и второго вычислительных блоков, выходы которых соединены соответственно с первыми входами первого и второго блоков умножения, ко вторым входам которых подключены n-е входы второго и первого операндов соответственно, а ко входам третьего вычислительного блока подсоединены n-е входы первого и второго операндов, причем выходы первого и второго блоков умножения и выход третьего вычислительного блока являются, соответственно, первым, вторым и третьим выходами n-го устройства вычисления остатка по n-му основанию, при этом выходы устройств вычисления остатков подключены ко входам сумматора 3N чисел по модулю mn, выход которого является выходом n-го блока вычисления остатка.
) первого и второго вычислительных блоков, выходы которых соединены соответственно с первыми входами первого и второго блоков умножения, ко вторым входам которых подключены n-е входы второго и первого операндов соответственно, а ко входам третьего вычислительного блока подсоединены n-е входы первого и второго операндов, причем выходы первого и второго блоков умножения и выход третьего вычислительного блока являются, соответственно, первым, вторым и третьим выходами n-го устройства вычисления остатка по n-му основанию, при этом выходы устройств вычисления остатков подключены ко входам сумматора 3N чисел по модулю mn, выход которого является выходом n-го блока вычисления остатка.
| Устройство для масштабирования чисел в остаточной системе счисления | 1983 |
|
SU1140114A1 |
| Устройство для масштабирования чисел | 1989 |
|
SU1667066A1 |
| Устройство для масштабирования чисел в модулярной арифметике | 1988 |
|
SU1541605A1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЛИАДИЧЕСКИЙ КОД | 2001 |
|
RU2187886C1 |
| US 5493522 А, 20.02.1996. | |||
Авторы
Даты
2005-02-20—Публикация
2002-12-30—Подача