Изобретение относится к автоматике и вычислительной технике и может найти применение в специализированных вычислительных и информационно-измерительных системах, в системах автоматического управления при воспроизведении и вычислении методом кусочно-квадратичной аппроксимации монотонных функций, аргумент которых представлен аналоговой величиной.
Известен аппроксиматор монотонных функций, аргумент которых представлен аналоговой величиной, содержащий блок преобразования напряжения в пачку импульсов, блок синхронизации, постоянное запоминающее устройство, сумматор и регистр [1].
Этому аппроксиматору также свойственна пониженная точность воспроизведения функциональных зависимостей, обусловленная применением метода кусочно-линейной аппроксимации.
Наиболее близким техническим решением, выбранным в качестве прототипа, является аппроксиматор монотонных функций, аргумент которых представлен аналоговой величиной, содержащий генератор импульсов, подключенный через последовательно соединенные управляемый делитель частоты, уравновешивающий счетчик и цифроаналоговый преобразователь к первому входу элемента сравнения, второй вход которого подключен к информационному входу аппроксиматора, а выход элемента сравнения подключен ко входу управления записью выходного регистра, установочные входы которого подключены к разрядным выходам счетчика функции параллельно входам преобразователя кодов, включающего в себя дешифратор номера участка, блока памяти, генератор импульсов высокой частоты, элементы И, ИЛИ, счетчик импульсов, триггер, регистр и формирователь [2].
Одним из недостатков прототипа является ограниченная область применения ввиду воспроизведения только монотонно возрастающих функций. Другим его недостатком является пониженная точность воспроизведения функциональных зависимостей, обусловленная, как и в аналогах, применением метода кусочно-линейной аппроксимации.
Целью изобретения является повышение точности воспроизведения за счет реализации кусочно-квадратичной аппроксимации.
На чертеже представлена функциональная схема аппроксиматора.
Аппроксиматор монотонных функций содержит счетчик 1 функции, счетчик 2 импульсов и преобразователь 3 кода в частоту, управляемый делитель 4 частоты, выполненный в виде последовательно соединенных кодовыми шинами мультиплексора 5 и преобразователя 6 кода в частоту, последовательно соединенные счетчик 7 длины участка и счетчик 8 номера участка, ключ 9, генератор 10 импульсов и преобразователь 11 напряжения в интервал времени, вход аргумента 12 аппроксиматора, вход 13 запуска, первый 14, второй 15 и третий 16 установочные входы аппроксиматора.
Функцию воспроизведения, диапазон изменения аргумента которой разбит на m равных по длине участков, каждый из которых аппроксимирован полиномом второй степени, на любом i-ом участке аппроксимации можно представить в виде
Y = a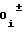 a
a Ux-U
Ux-U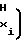 ± a
± a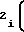 Ux-U
Ux-U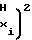 (1) причем U
(1) причем U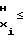 Ux≅ U
Ux≅ U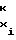 1≅i≅m , где Y - функция воспроизведения;
1≅i≅m , где Y - функция воспроизведения;
Ux - напряжение аргумента;
U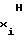 , U
, U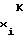 - напряжения аргумента в начальной и конечной точках i-го участка соответственно;
- напряжения аргумента в начальной и конечной точках i-го участка соответственно;
a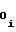 , a
, a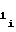 , a
, a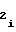 - постоянные коэффициенты, соответствующие i-му участку, причем знаки полярности перед коэффициентамиa
- постоянные коэффициенты, соответствующие i-му участку, причем знаки полярности перед коэффициентамиa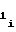 и a
и a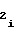 могут принимать различные, но одинаковые для всех m участков сочетания за исключением тех, при которых в диапазоне изменения напряжения Ux аргумента происходит изменение знака полярности первой либо второй производных функции воспроизведения (1), т. е. рассматривается только такая функция воспроизведения, которая монотонна и не имеет точек перегиба.
могут принимать различные, но одинаковые для всех m участков сочетания за исключением тех, при которых в диапазоне изменения напряжения Ux аргумента происходит изменение знака полярности первой либо второй производных функции воспроизведения (1), т. е. рассматривается только такая функция воспроизведения, которая монотонна и не имеет точек перегиба.
Необходимо отметить, что разбиение на участки диапазона изменения напряжения Ux аргумента должно производиться при условии не только, как отмечалось выше, равенства их длины ΔUx
ΔUx= U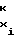 - U
- U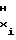 = const (2) но и при условии, чтобы в узлах аппроксимации функция воспроизведения (1) не претерпевала разрыва, т.е. чтобы соблюдалось равенство
= const (2) но и при условии, чтобы в узлах аппроксимации функция воспроизведения (1) не претерпевала разрыва, т.е. чтобы соблюдалось равенство
a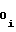 = a
= a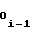 + ΔYi-1, (3) где
+ ΔYi-1, (3) где
ΔYi-1= ± a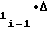 Ux± a
Ux± a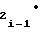 ΔU
ΔU
Цикл воспроизведения и вычисления монотонной функции, представленной формулой (1), начинается с поступления на шину 13 запуска аппроксиматора импульса, запускающего по управляющему входу преобразователь 11 напряжения в интервал времени (ПНИВ) и производящего запись кодовых уставокA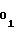 иA
иA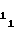 с первого 14 и второго 15 установочных входов в счетчик 1 функции и в счетчик 2 импульсов соответственно (цепи записи счетчиков на чертеже не показаны). Для обеспечения более четкой работы аппроксиматора запись кодовых уставокA
с первого 14 и второго 15 установочных входов в счетчик 1 функции и в счетчик 2 импульсов соответственно (цепи записи счетчиков на чертеже не показаны). Для обеспечения более четкой работы аппроксиматора запись кодовых уставокA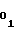 иA
иA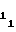 должна производиться передним фронтом запускающего импульса, а запуск ПНИВ 11 - задним, либо запись указанных кодов должна производиться заранее перед запускающим импульсом, как операция по установке счетчиков 1 и 2 в исходное состояние. На выходе ПНИВ 11 формируется импульс напряжения, длительность Т которого пропорциональна напряжению Ux аргумента на входе 12 аппроксиматора, поступающему на информационный вход ПНИВ 11
должна производиться передним фронтом запускающего импульса, а запуск ПНИВ 11 - задним, либо запись указанных кодов должна производиться заранее перед запускающим импульсом, как операция по установке счетчиков 1 и 2 в исходное состояние. На выходе ПНИВ 11 формируется импульс напряжения, длительность Т которого пропорциональна напряжению Ux аргумента на входе 12 аппроксиматора, поступающему на информационный вход ПНИВ 11
Т = k˙ Ux , (5) где k - коэффициент преобразования ПНИВ 11.
Учитывая непрерывность и линейность преобразования напряжения Uxаргумента в интервал времени, можно считать справедливыми выражения
Ti= k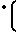 Ux-U
Ux-U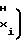 (6)
(6)
ΔТ = k ˙ΔUx, (7) где Тi - время преобразования, пропорциональное разности текущего и начального значений напряжения Ux на i-ом участке;
ΔТ - время преобразования, пропорциональное длине участка ΔUx.
Выходной импульс ПНИВ 11, поступая на управляющий вход ключа 9, открывает последний, в результате чего импульсы с генератора 10 импульсов, приходящие на информационный вход ключа 9, поступают на частотные входы преобразователей 3 и 6 кода в частоту (ПКЧ).
Выходная частотаf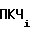 ПКЧ 3 на i-ом участке определяется выражением
ПКЧ 3 на i-ом участке определяется выражением
f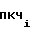 =
= 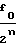 · N
· N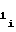 , (8) где fo - частота генератора 10 импульсов;
, (8) где fo - частота генератора 10 импульсов;
n - число разрядов ПКЧ 3, равное числу разрядов счетчика 2 импульсов;
N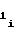 - выходной код счетчика 2 импульсов на i-ом участке.
- выходной код счетчика 2 импульсов на i-ом участке.
В каждый момент времени t в интервале длительности Ti на любом i-ом участке выходной кодN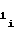 счетчика 2 импульсов, поступающий на кодовые шины ПКЧ 3, будет равен
счетчика 2 импульсов, поступающий на кодовые шины ПКЧ 3, будет равен
N = A
= A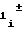 f
f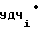 t (9) причем
t (9) причем
A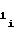 = A
= A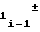 f
f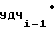 ΔT (10)
ΔT (10)
f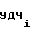 =
= 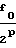 A
A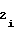 , (11) где A
, (11) где A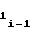 ,A
,A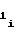 - выходные коды счетчика 2 импульсов, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках;
- выходные коды счетчика 2 импульсов, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках;
f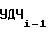 , f
, f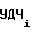 - выходные частоты управляемого делителя 4 частоты (УДЧ) на i-1-ом и i-ом участках соответственно, равные выходным частотам ПКЧ 6;
- выходные частоты управляемого делителя 4 частоты (УДЧ) на i-1-ом и i-ом участках соответственно, равные выходным частотам ПКЧ 6;
P - число разрядов ПКЧ 6, равное числу разрядов мультиплексора 5;
A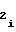 - выходной код мультиплексора 5 на i-ом участке. Знаки полярности "+" либо "-" в выражениях (9) и (10) употребляются в зависимости от режима, в котором должен работать счетчик 2 импульсов - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 2 импульсов в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A
- выходной код мультиплексора 5 на i-ом участке. Знаки полярности "+" либо "-" в выражениях (9) и (10) употребляются в зависимости от режима, в котором должен работать счетчик 2 импульсов - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 2 импульсов в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A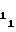 . Подставляя выражение (9) в (8) и используя формулу (11), получаем
. Подставляя выражение (9) в (8) и используя формулу (11), получаем
f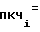
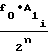 ±
± 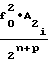 · t (12)
· t (12)
С частотного выхода ПКЧ 3 за время преобразования Тi на вход счетчика 1 функции поступит число импульсов Ni, равное
Ni= 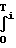 f
f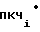 dt (13) Подставляя формулу (12) в (13) и производя интегрирование с использованием выражения (6), получаем
dt (13) Подставляя формулу (12) в (13) и производя интегрирование с использованием выражения (6), получаем
Ni=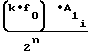 ·
· 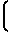 Ux-U
Ux-U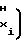 ±
± 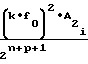 ·
· 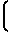 Ux-U
Ux-U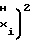 (14) К моменту окончания длительности Т, соответствующему концу цикла воспроизведения и вычисления монотонной функции, выходной код NYсчетчика 1 функции будет соответствовать числу импульсов, равному
(14) К моменту окончания длительности Т, соответствующему концу цикла воспроизведения и вычисления монотонной функции, выходной код NYсчетчика 1 функции будет соответствовать числу импульсов, равному
NY= A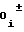 Ni (15) причем, в силу плавности воспроизведения, характеризуемого отсутствием записи каких-либо чисел в этот счетчик в моменты прохождения узлов аппроксимации, что приводило бы к скачкообразному изменению (разрыву) его выходного кода, будут справедливы с учетом формулы (7) равенства, соответствующие условию непрерывности функции воспроизведения (1) согласно выражениям (3) и (4)
Ni (15) причем, в силу плавности воспроизведения, характеризуемого отсутствием записи каких-либо чисел в этот счетчик в моменты прохождения узлов аппроксимации, что приводило бы к скачкообразному изменению (разрыву) его выходного кода, будут справедливы с учетом формулы (7) равенства, соответствующие условию непрерывности функции воспроизведения (1) согласно выражениям (3) и (4)
A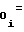 A
A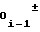 Ni-1 (16)
Ni-1 (16)
Ni-1= 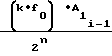 · ΔUx ±
· ΔUx ± 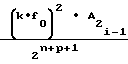 ΔU
ΔU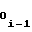 ,A
,A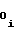 - выходные коды счетчика 1 функции, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках. Знаки полярности "+" либо "-" в выражениях (15) и (16) употребляются в зависимости от режима, в котором должен работать счетчик 1 функции - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 1 функции в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A
- выходные коды счетчика 1 функции, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках. Знаки полярности "+" либо "-" в выражениях (15) и (16) употребляются в зависимости от режима, в котором должен работать счетчик 1 функции - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 1 функции в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A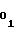 .
.
Учитывая выражение (14), формулу (15) запишем в виде
NY = A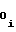 ±
± 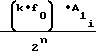
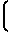 Ux-U
Ux-U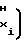 ±
± 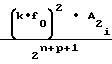
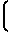 Ux-U
Ux-U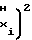 (18)
(18)
Сопоставляя формулы (1) и (18), можно отметить, что при соблюдении равенств
a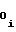 =
=  A
A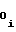 (19)
(19)
a =
= 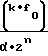 A
A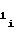 (20)
(20)
a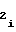 =
= 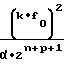 A
A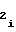 (21) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (1), аргумент которой представлен напряжением
(21) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (1), аргумент которой представлен напряжением
NY = α˙Y (22) где α- коэффициент масштабирования.
Для удобства отсчета результата вычисления счетчик 1 функции может быть выполнен двоично-десятичным, а коэффициент α выбран кратным десяти.
Соблюдение равенства (19) при заданномα обеспечивается путем выбора величины начальной уставки A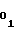 , соответствующей коэффициентуa
, соответствующей коэффициентуa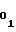 первого участка аппроксимации, и выполнения равенств (20) и (21) для каждого из m участков, необходимость выполнения которых вытекает из формул (3), (4), (16) и (17).
первого участка аппроксимации, и выполнения равенств (20) и (21) для каждого из m участков, необходимость выполнения которых вытекает из формул (3), (4), (16) и (17).
В свою очередь соблюдение равенства (20) при заданных α, k, fo, n обеспечивается путем выбора величины начальной уставки A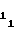 , соответствующей коэффициенту a
, соответствующей коэффициенту a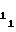 первого участка аппроксимации, и выполнения для последующих участков определенного соотношения между значением коэффициентаa
первого участка аппроксимации, и выполнения для последующих участков определенного соотношения между значением коэффициентаa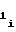 i-го участка и значениями коэффициентов a
i-го участка и значениями коэффициентов a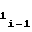 иa
иa i-1-го участка, которое сводится к следующему.
i-1-го участка, которое сводится к следующему.
Учитывая равенства (7), (11) и (20), формулу (10) запишем в виде
a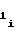 = a
= a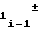
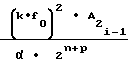 ΔUx (23)
ΔUx (23)
Используя равенство (21), получаем соотношение
a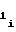 = a
= a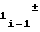 2 · a2i-1ΔUx (24) т.е. при разбиении на участки диапазона изменения напряжения Uxаргумента значение коэффициентаa
2 · a2i-1ΔUx (24) т.е. при разбиении на участки диапазона изменения напряжения Uxаргумента значение коэффициентаa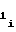 i-го участка должно определяться по значениям коэффициентов a
i-го участка должно определяться по значениям коэффициентов a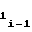 иa
иa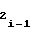 предшествующего i-1-го участка. При этом нетрудно убедиться, что соблюдение соотношения (24) равносильно необходимости соблюдения в узлах аппроксимации непрерывности первой производной функции воспроизведения (1) при разбиении ее на участки, т.е. необходимости выполнения равенства
предшествующего i-1-го участка. При этом нетрудно убедиться, что соблюдение соотношения (24) равносильно необходимости соблюдения в узлах аппроксимации непрерывности первой производной функции воспроизведения (1) при разбиении ее на участки, т.е. необходимости выполнения равенства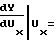
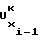 =
= 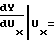
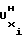 (25)
(25)
Таким образом разбиение на участки диапазона изменения напряжения Ux аргумента должно производиться при условии отсутствия в узлах аппроксимации разрыва не только функции воспроизведения (1), но и ее первой производной, т. е. вышеуказанное разбиение должно осуществляться путем сплайн-аппроксимации полиномами второй степени.
Что касается соблюдения равенства (21) при заданных α, k, fo, n, p, то оно обеспечивается установлением числаA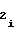 на входе ПКЧ 6 в начальный момент аппроксимации i-го участка, что достигается следующим образом. В момент начала формирования интервала времени Т импульсы с частотой foначинают поступать с выхода ключа 9 на вход предварительно обнуленного (цепь сброса на чертеже не показана) счетчика 7 длины участка, период Тпповторения выходных импульсов которого равен
на входе ПКЧ 6 в начальный момент аппроксимации i-го участка, что достигается следующим образом. В момент начала формирования интервала времени Т импульсы с частотой foначинают поступать с выхода ключа 9 на вход предварительно обнуленного (цепь сброса на чертеже не показана) счетчика 7 длины участка, период Тпповторения выходных импульсов которого равен
Tп= 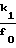 , (26) где k1 - коэффициент пересчета счетчика 7 длины участка. Период Тп выбирается таким, чтобы он был равен времени преобразования ΔТ длины участка ΔUx, т.е. чтобы выполнялось равенство
, (26) где k1 - коэффициент пересчета счетчика 7 длины участка. Период Тп выбирается таким, чтобы он был равен времени преобразования ΔТ длины участка ΔUx, т.е. чтобы выполнялось равенство
k1 = k˙ fo ΔUx (27) Выходные импульсы счетчика 7 длины участка с периодом Тп поступают на вход счетчика 8 номера участка, в результате чего последний поочередно устанавливается в одно из m состояний, начиная со второго. Установка счетчика 8 номера участка в первое состояние, соответствующее первому участку, и, тем, самым, дальнейшее установление соответствия между номерами участков и состояниями счетчика 8 номера участка, производится путем подачи импульса обнуления (цепь сброса на чертеже не показана) в тот же момент, что и для счетчика 7 длины участка, а, именно, перед запуском ПНИВ 11, например, в момент записи начальных уставокA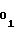 и A
и A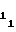 . Последовательно сменяемая по мере перехода с участка на участок кодовая комбинация с выходных шин счетчика 8 номера участка поступает на управляющие входы мультиплексора 5, в результате чего на выходе последнего в моменты перехода с i-1-го на i-ый участок устанавливается необходимое i-му участку числоA
. Последовательно сменяемая по мере перехода с участка на участок кодовая комбинация с выходных шин счетчика 8 номера участка поступает на управляющие входы мультиплексора 5, в результате чего на выходе последнего в моменты перехода с i-1-го на i-ый участок устанавливается необходимое i-му участку числоA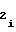 из ряда мультиплексируемых с третьего 16 установочного входа чисел A
из ряда мультиплексируемых с третьего 16 установочного входа чисел A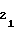 ...A
...A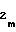 , шины которых соединены с информационными входами мультиплексора 5. Установление необходимых чиселA
, шины которых соединены с информационными входами мультиплексора 5. Установление необходимых чиселA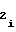 на входе ПКЧ 6 может производиться не только с помощью мультиплексора 5, но и с помощью, например, дешифратора, преобразователя кода на программируемой логической матрице или ПЗУ, в котором заранее "прошиты" вышеуказанные числа. При этом для каждого из заменяющих элементов входным кодом (для ПЗУ - адресным), как и для мультиплексора 5, является код выходных шин счетчика 8 номера участка, а их выходным кодом - код чисел A
на входе ПКЧ 6 может производиться не только с помощью мультиплексора 5, но и с помощью, например, дешифратора, преобразователя кода на программируемой логической матрице или ПЗУ, в котором заранее "прошиты" вышеуказанные числа. При этом для каждого из заменяющих элементов входным кодом (для ПЗУ - адресным), как и для мультиплексора 5, является код выходных шин счетчика 8 номера участка, а их выходным кодом - код чисел A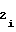 , полученный в результате операции дешифрирования, преобразования или выборки.
, полученный в результате операции дешифрирования, преобразования или выборки.
Таким образом реализация сплайн-аппроксимации функции воспроизводится (1) сводится к установлению в счетчиках 1 и 2 начальных уставокA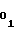 и A
и A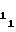 , соответствующих первому участку аппроксимации, и установлению с помощью мультиплексора 5 на кодовом входе ПКЧ 6 числа A
, соответствующих первому участку аппроксимации, и установлению с помощью мультиплексора 5 на кодовом входе ПКЧ 6 числа A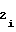 , соответствующего i-му участку, начиная с первого. При этом нет необходимости в начале каждого из последующих участков производить запись в счетчиках 1 и 2 чиселA
, соответствующего i-му участку, начиная с первого. При этом нет необходимости в начале каждого из последующих участков производить запись в счетчиках 1 и 2 чиселA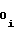 и A
и A , так как эти числа на кодовых выходах указанных счетчиков устанавливается автоматически в силу непрерывного (без скачков) или счета импульсов, соответствующего непрерывности функции воспроизведения (1) и ее первой производной, что, как отмечалось выше, характерно для сплайн-аппроксимации.
, так как эти числа на кодовых выходах указанных счетчиков устанавливается автоматически в силу непрерывного (без скачков) или счета импульсов, соответствующего непрерывности функции воспроизведения (1) и ее первой производной, что, как отмечалось выше, характерно для сплайн-аппроксимации.
Упоминаемые ранее режимы работы счетчиков 1 и 2 на сложение либо на вычитание устанавливаются заранее, исходя из знаков полярности производных функции воспроизведения (1), а, именно:
если знак полярности первой производной на любом без исключения i-ом участке положителен, т.е. если функция воспроизведения (1) монотонно возрастающая, то счетчик 1 функции необходимо устанавливать в режим сложения, а если отрицателен, то в режим вычитания;
если полярность произведения знаков полярности первой и второй производных на любом без исключения i-ом участке положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
Учитывая, что в аппроксиматоре рассматривается функция воспроизведения (1), у которой полярность первой и второй производных неизменна во всем диапазоне изменения напряжения Ux аргумента, в том числе и при Ux=U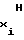 , учет знаков полярности вышеуказанных производных при выборе режимов работы счетчиков 1 и 2 можно заменить на более простой учет знаков полярности перед коэффициентами a
, учет знаков полярности вышеуказанных производных при выборе режимов работы счетчиков 1 и 2 можно заменить на более простой учет знаков полярности перед коэффициентами a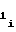 и a
и a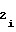 функции воспроизведения (1), каждый из которых, как указывалось выше, одинаков для любого из m участков, а, именно:
функции воспроизведения (1), каждый из которых, как указывалось выше, одинаков для любого из m участков, а, именно:
если перед коэффициентомa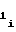 знак "+", то счетчик 1 функции необходимо устанавливать в режим сложения, а если знак "-", то в режим вычитания;
знак "+", то счетчик 1 функции необходимо устанавливать в режим сложения, а если знак "-", то в режим вычитания;
если полярность произведения знаков полярности перед коэффициентамиa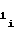 и a
и a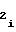 положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
Необходимо подчеркнуть, что, в силу одинаковости знаков полярности перед одноименными коэффициентами функции воспроизведения (1) на каждом из m ее участков, режимы работы счетчиков 1 и 2 на сложение либо на вычитание, заранее устанавливаемые согласно вышеуказанным знакам, также одинаковы на каждом из этих участков.
Следует отметить, что если функция воспроизведения (1) представлена в более краткой форме
Y = b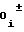 b
b Ux± b
Ux± b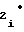 U
U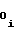 ,b
,b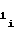 ,b
,b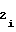 - постоянные коэффициенты, то связь между приведенными коэффициентами и коэффициентами a
- постоянные коэффициенты, то связь между приведенными коэффициентами и коэффициентами a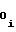 ,a
,a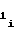 и a
и a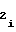 можно выразить соотношениями
можно выразить соотношениями
b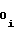 = a
= a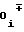 a
a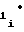 U
U a
a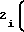 U
U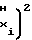 (29)
(29)
b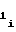 = a
= a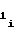 -2 · a
-2 · a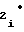 U
U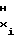 (30)
(30)
b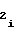 = a
= a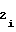 (31) Учитывая прямо пропорциональную зависимость длительности Т интервала времени от напряжения Ux аргумента, можно отметить, что на первом участке при Т = 0 напряжение аргумента U
(31) Учитывая прямо пропорциональную зависимость длительности Т интервала времени от напряжения Ux аргумента, можно отметить, что на первом участке при Т = 0 напряжение аргумента U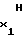 =0. При этом выражения (29)... (31) для первого участка примут вид
=0. При этом выражения (29)... (31) для первого участка примут вид
b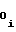 = a
= a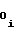 (32) b
(32) b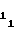 = a
= a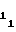 (33) b
(33) b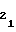 = a
= a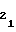 (34) т.е. для первого участка имеет место идентичность рассматриваемых коэффициентов, согласно которым, как указывалось выше, устанавливаются начальные уставки A
(34) т.е. для первого участка имеет место идентичность рассматриваемых коэффициентов, согласно которым, как указывалось выше, устанавливаются начальные уставки A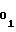 , A
, A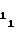 и A
и A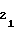 число .
число .
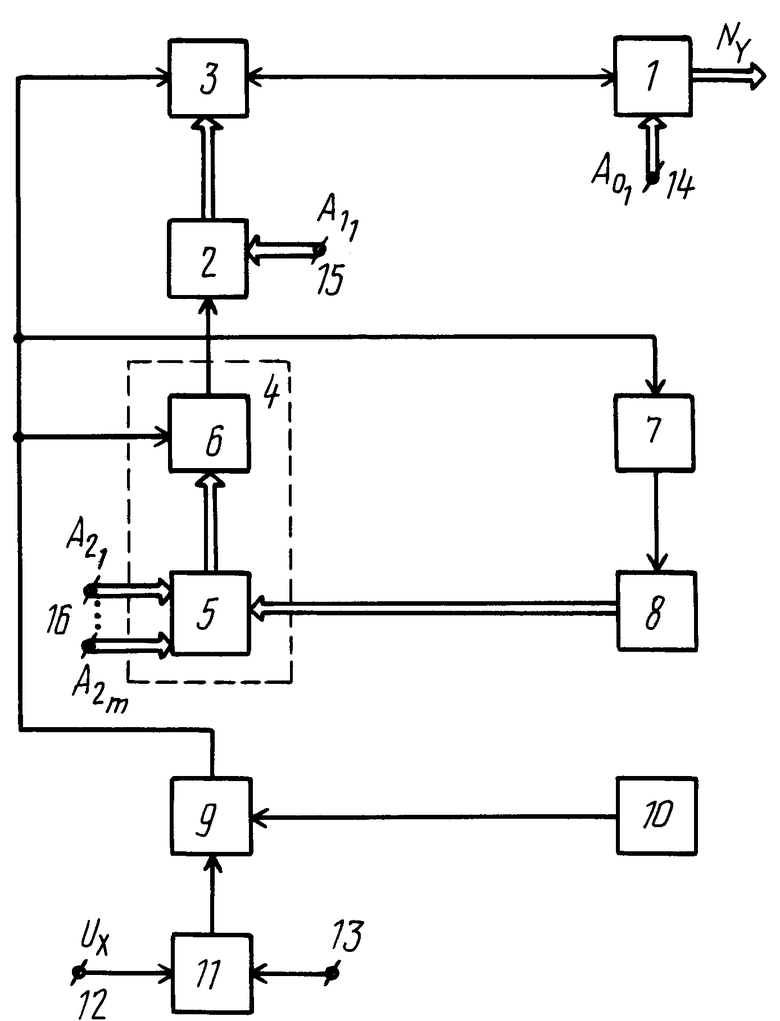
Таким образом, благодаря новым связям, элементам и возможности установки различного сочетания режимов работы счетчиков 1 и 2, обеспечивается с учетом масштабирования аппаратурная реализация воспроизведения и вычисления монотонных функций, как возрастающих, так и убывающих, выпуклых как вверх, так и вниз (в зависимости от знака полярности перед коэффициентом a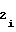 ), воспроизводимых путем сплайн-аппроксимации, и аргумент которых может быть представлен аналоговой величиной, например, напряжением. Кроме того повышается точность воспроизведения функции за счет реализации кусочно-квадратичной аппроксимации, как более точной по сравнению с кусочно-линейной, применяемой в прототипе.
), воспроизводимых путем сплайн-аппроксимации, и аргумент которых может быть представлен аналоговой величиной, например, напряжением. Кроме того повышается точность воспроизведения функции за счет реализации кусочно-квадратичной аппроксимации, как более точной по сравнению с кусочно-линейной, применяемой в прототипе.
| название | год | авторы | номер документа |
|---|---|---|---|
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2023296C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2023298C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2018947C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2018948C1 |
| Устройство для измерения температуры | 1990 |
|
SU1809328A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721606A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721604A1 |
| Устройство для измерения температуры | 1988 |
|
SU1642270A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721605A1 |
| Устройство для измерения температуры | 1990 |
|
SU1809330A1 |
Изобретение относится к автоматике и вычислительной технике и может найти применение в специализированных вычислительных и информационно-измерительных системах. Целью изобретения является повышение точности за счет реализации кусочно-квадратичной зависимости. Аппроксиматор содержит генератор импульсов, управляемый делитель частоты, счетчик импульсов, счетчик функции, преобразователь напряжения в интервал времени, ключ, преобразователь кода в частоту, последовательно соединенные счетчики длины и номер участка, а управляемый делитель частоты выполнен в виде последовательно соединенных кодовыми шинами мультиплексора и преобразователя кода в частоту. 1 ил.
АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ, содержащий генератор импульсов, управляемый делитель частоты, счетчик импульсов и счетчик функции, отличающийся тем, что, с целью повышения точности путем реализации кусочно-квадратичной аппроксимации, он содержит ключ, преобразователь кода в частоту, счетчик номера участка, счетчик длины участка и преобразователь напряжения в интервал времени, причем выход генератора импульсов соединен с информационным входом ключа, управляющий вход которого соединен с выходом преобразователя напряжения в интервал времени, управляющий и информационный входы которого соединены соответственно с входом запуска и входом аргумента аппроксиматора, выход и первый установочный вход которого соединены соответственно с выходом и информационным входом счетчика функции, счетный вход которого соединен с выходом преобразователя кода в частоту, частотный вход которого соединен с выходом ключа, частотным входом управляемого делителя частоты и счетным входом счетчика длины участка, выход которого соединен со счетным входом счетчика номера участка, выход которого соединен с управляющим входом управляемого делителя частоты, выход которого соединен со счетным входом счетчика импульсов, выход и информационный вход которого соединены соответственно с информационным входом преобразователя кода в частоту и вторым установочным входом аппроксиматора, третий установочный вход которого соединен с информационным входом управляемого делителя частоты.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Аналого-цифровой функциональный преобразователь | 1976 |
|
SU567203A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1994-11-15—Публикация
1991-06-28—Подача