Изобретение относится к автоматике и вычислительной технике и может найти применение в специализированных вычислительных и информационно-измерительных системах, в системах автоматического управления при воспроизведении и вычислении методом кусочно-квадратичной аппроксимации монотонных функций, аргумент которых представлен частотой либо ее периодом.
Известен аппроксиматор монотонных функций, аргумент которых представлен частотой, содержащий преобразователь кода в частоту, включающий в себя счетчик импульсов и группу вентилей, управляемый делитель частоты, включающий в себя счетчик импульсов, группу вентилей и ключ, последовательно соединенные кодовыми шинами счетчик числа участков, дешифратор кодов и запоминающее устройство, удвоитель частоты и элемент ИЛИ [1].
Недостатком аппроксиматора является невысокая точность воспроизведения функциональных зависимостей, обусловленная применением метода кусочно-линейной аппроксимации, который хотя и точнее ступенчатой аппроксимации, но уступает кусочно-квадратичной.
Наиболее близким техническим решением, выбранным в качестве прототипа, является аппроксиматор монотонных функций, аргумент которых представлен частотой, содержащий формирователь прямоугольных импульсов, вход и выход которого соединены соответственно со входом аппроксиматора и управляющим входом ключа, генератор импульсов, выход которого соединен с информационным входом ключа, дифференцирующие элементы, последовательно соединенные кодовыми шинами счетчик длины участка, дешифратор участков, дешифратор приращений, сумматор, регистр и цифроаналоговый преобразователь, и элемент задержки, причем выход ключа соединен со счетным входом счетчика длины участка [2].
Одним из недостатков прототипа является, по-прежнему, пониженная точность воспроизведения функциональных зависимостей, обусловленная применением метода кусочно-линейной аппроксимации. Другим его недостатком является ограниченный класс решаемых задач, обусловленный тем, что, во-первых, аргумент вышеуказанных зависимостей ограничен только частотой, а, во-вторых, воспроизведение этих зависимостей ограничивается только монотонно возрастающими функциями.
Целью изобретения является повышение точности воспроизведения за счет реализации кусочно-квадратичной аппроксимации.
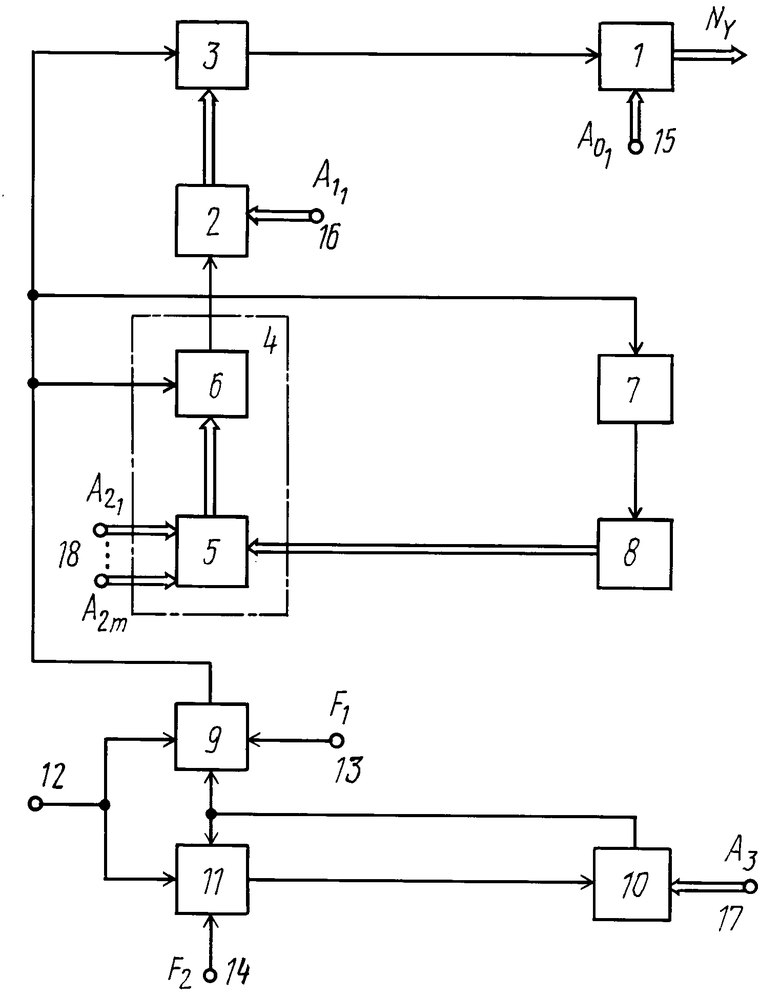
На чертеже представлена функциональная схема аппроксиматора.
Аппроксиматор монотонных функций содержит счетчик 1 функции, счетчик 2 импульсов и преобразователь 3 кода в частоту, управляемый делитель 4 частоты, выполненный в виде последовательно соединенных кодовыми шинами мультиплексора 5 и преобразователя 6 кода в частоту, последовательно соединенные счетчик 7 длины участка и счетчик 8 номера участка, первый ключ 9, второй счетчик 10 импульсов и второй ключ 11, вход 12 запуска аппроксиматора, первый 13 и второй 14 входы аргумента аппроксиматора, первый 15, второй 16, третий 17 и четвертый 18 установочные выходы аппроксиматора.
Функцию воспроизведения, диапазон изменения аргумента которой разбит на m равных по длине участков, каждый из которых аппроксимирован полиномом второй степени, на любом i-ом участке аппроксимации можно представить в виде
Y = a0 ± a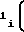 Fx-F
Fx-F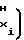 ± a
± a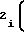 Fx-F
Fx-F (1) либо в виде
(1) либо в виде
Y = b b
b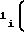 Tx-T
Tx-T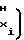 ± b
± b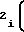 Tx-T
Tx-T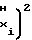 (2) причем
(2) причем
F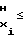 Fx≅ F
Fx≅ F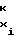 T
T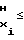 Tx≅ T
Tx≅ T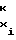 1
1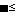 i ≅ m, где Y - функция воспроизведения;
i ≅ m, где Y - функция воспроизведения;
Fx - частота аргумента на первом входе 13 аппроксиматора;
F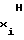 , F
, F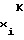 - частоты аргумента в начальной и конечной точках i-го участка соответственно;
- частоты аргумента в начальной и конечной точках i-го участка соответственно;
Тx - период частоты аргумента на втором входе 14 аппроксиматора;
T , T
, T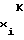 - периоды частоты аргумента в начальной и конечной точках i-го участка соответственно;
- периоды частоты аргумента в начальной и конечной точках i-го участка соответственно;
a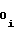 , a
, a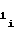 ,a
,a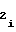 - постоянные коэффициенты, соответствующие i-му b
- постоянные коэффициенты, соответствующие i-му b ,b
,b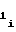 ,b
,b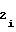 участку, причем знаки полярности перед коэффициентами a
участку, причем знаки полярности перед коэффициентами a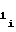 ,a
,a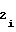 ,b
,b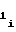 ,b
,b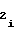 могут принимать различные, но одинаковые для всех m участков сочетания за исключением тех, при которых в диапазоне изменения частоты Fx или периода Tx аргумента происходит изменение знака полярности первой либо второй производных функции воспроизведения (1) либо (2), т.е. рассматривается только такая функция воспроизведения, которая монотонна и не имеет точек перегиба.
могут принимать различные, но одинаковые для всех m участков сочетания за исключением тех, при которых в диапазоне изменения частоты Fx или периода Tx аргумента происходит изменение знака полярности первой либо второй производных функции воспроизведения (1) либо (2), т.е. рассматривается только такая функция воспроизведения, которая монотонна и не имеет точек перегиба.
Необходимо отметить, что разбиение на участки диапазона изменения частоты Fx или периода Tx аргумента должно производиться при условии не только, как отмечалось выше, равенства их длины ΔFx либо ΔTx
ΔFx= F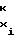 - F
- F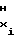 = const (3)
= const (3)
ΔTx= T - T
- T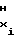 = const (4) но и при условии, чтобы в узлах аппроксимации функция воспроизведения (1) либо (2) не претерпевала разрыва, т.е. чтобы соблюдались равенства
= const (4) но и при условии, чтобы в узлах аппроксимации функция воспроизведения (1) либо (2) не претерпевала разрыва, т.е. чтобы соблюдались равенства
a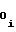 = a
= a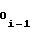 + ΔYi-1 (5) либо
+ ΔYi-1 (5) либо
b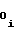 = b
= b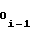 + ΔYi-1 (6)
+ ΔYi-1 (6)
ΔYi-1= ± a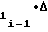 Fx± a
Fx± a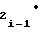 ΔF
ΔF
ΔYi-1= ± b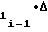 Tx± b
Tx± b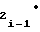 ΔT
ΔT
Цикл воспроизведения и вычисления монотонной функции, представленной формулой (1) либо (2), начинается с поступления на шину 12 запуска аппроксиматора импульса, который по управляющим входам первого 9 и второго 11 ключей открывает последние и производит запись кодовых уставокA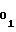 ,A
,A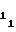 и A3 с первого 15, второго 16 и третьего 17 установочных входов в счетчики 1, 2 и 10 соответственно (цепи записи счетчиков на чертеже не показаны). Причем, если запись кодовой уставки A3 производится в прямом коде, то второй счетчик 10 импульсов устанавливается заранее в режим вычитания, а если в дополнительном - то в режим сложения. Для обеспечения более четкой работы аппроксиматора запись кодовых уставокA
и A3 с первого 15, второго 16 и третьего 17 установочных входов в счетчики 1, 2 и 10 соответственно (цепи записи счетчиков на чертеже не показаны). Причем, если запись кодовой уставки A3 производится в прямом коде, то второй счетчик 10 импульсов устанавливается заранее в режим вычитания, а если в дополнительном - то в режим сложения. Для обеспечения более четкой работы аппроксиматора запись кодовых уставокA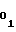 , A
, A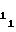 и A3 должна производиться передним фронтом запускающего импульса, а открытие ключей 9 и 11 - задним, либо запись указанных кодов должна производиться заранее перед запускающим импульсом, как операция по установке счетчиков 1, 2 и 10 в исходное состояние. При этом импульсы частотой F1, поступающие с первого входа 13 аппроксиматора на информационный вход первого ключа 9, проходя через последний, поступают на частотные входы преобразователей 3 и 6 кода в частоту (ПКЧ), а импульсы частотой F2, поступающие со второго входа 14 аппроксиматора на информационный вход второго ключа 11, проходя через последний, поступают на счетный вход второго счетчика 10 импульсов. При обнулении вышеуказанного счетчика (режим вычитания) либо переполнении (режим сложения) его выходной импульс по входам блокировки первого 9 и второго 11 ключей закрывает последние, в результате чего прекращается цикл воспроизведения, длительность Т которого определяется формулой
и A3 должна производиться передним фронтом запускающего импульса, а открытие ключей 9 и 11 - задним, либо запись указанных кодов должна производиться заранее перед запускающим импульсом, как операция по установке счетчиков 1, 2 и 10 в исходное состояние. При этом импульсы частотой F1, поступающие с первого входа 13 аппроксиматора на информационный вход первого ключа 9, проходя через последний, поступают на частотные входы преобразователей 3 и 6 кода в частоту (ПКЧ), а импульсы частотой F2, поступающие со второго входа 14 аппроксиматора на информационный вход второго ключа 11, проходя через последний, поступают на счетный вход второго счетчика 10 импульсов. При обнулении вышеуказанного счетчика (режим вычитания) либо переполнении (режим сложения) его выходной импульс по входам блокировки первого 9 и второго 11 ключей закрывает последние, в результате чего прекращается цикл воспроизведения, длительность Т которого определяется формулой
T = 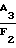 (9)
(9)
Учитывая непрерывность и линейность преобразования кодовой уставки А3 в интервал времени, можно считать справедливыми выражения для случая F2 = const
Ti=  (10)
(10)
ΔT = 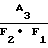 · ΔF1 (11) либо для случая F1 = const
· ΔF1 (11) либо для случая F1 = const
Ti= A3· 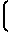 T2-T
T2-T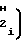 (12)
(12)
ΔT = A3 ˙ΔT2, (13) где Ti - время преобразования, пропорциональное разности текущего и начального значений частоты F1 либо периода T2 частоты на i-ом участке;
ΔТ - время преобразования, пропорциональное длине участка ΔF1 либо ΔТ2.
Выходная частотаf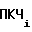 ПКЧ 3 на i-ом участке определяется выражением
ПКЧ 3 на i-ом участке определяется выражением
f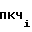 =
= 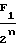 · N
· N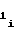 , (14) где n - число разрядов ПКЧ 3, равное числу разрядов счетчика 2 импульсов;
, (14) где n - число разрядов ПКЧ 3, равное числу разрядов счетчика 2 импульсов;
N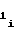 - выходной код счетчика 2 импульсов на i-ом участке.
- выходной код счетчика 2 импульсов на i-ом участке.
В каждый момент времени t в интервале длительности Ti на любом i-ом участке выходной кодN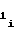 счетчика 2 импульсов, поступающий на кодовые шины ПКЧ 3, будет равен
счетчика 2 импульсов, поступающий на кодовые шины ПКЧ 3, будет равен
N = A
= A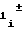 f
f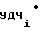 t (15) причем
t (15) причем
A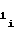 = A
= A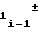 f
f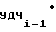 ΔT (16)
ΔT (16)
f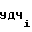 =
=  · A
· A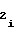 (17) где A
(17) где A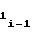 ,A
,A - выходные коды счетчика 2 импульсов, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках;
- выходные коды счетчика 2 импульсов, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках;
f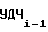 , f
, f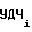 - выходные частоты управляемого делителя 4 частоты (УДЧ) на i-1-ом и i-ом участках соответственно, равные выходным частотам ПКЧ 6;
- выходные частоты управляемого делителя 4 частоты (УДЧ) на i-1-ом и i-ом участках соответственно, равные выходным частотам ПКЧ 6;
p - число разрядов ПКЧ 6, равное числу разрядов мультиплексора 5;
A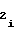 - выходной код мультиплексора 5 на i-ом участке. Знаки полярности "+" либо "-" в выражениях (15) и (16) употребляются в зависимости от режима, в котором должен работать счетчик 2 импульсов - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 2 импульсов в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A
- выходной код мультиплексора 5 на i-ом участке. Знаки полярности "+" либо "-" в выражениях (15) и (16) употребляются в зависимости от режима, в котором должен работать счетчик 2 импульсов - в суммирующем либо в вычитающем соответственно, при этом выходной код счетчика 2 импульсов в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A
Подставляя выражение (15) в (14) и используя формулу (17), получаем
f =
= 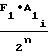 ±
± 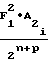 · t (18)
· t (18)
С частотного выхода ПКЧ 3 за время преобразования Ti на вход счетчика 1 функции поступит число импульсов Ni, равное
Ni=  f
f dt (19) Подставляя формулу (18) в (19) и производя интегрирование с использованием выражений (10), (12) получаем
dt (19) Подставляя формулу (18) в (19) и производя интегрирование с использованием выражений (10), (12) получаем
для случая F2 = const
Ni= 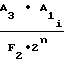 ·
· 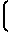 F1-F
F1-F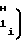 ±
± 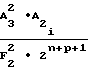 ·
· 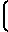 F1-F
F1-F (20)
(20)
либо для случая F1 = const
Ni= 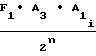 ·
· 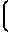 T2-T
T2-T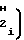 ±
± 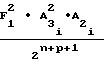 ·
·  T2-T
T2-T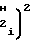 (21) К моменту окончания длительности Т, соответствующему концу цикла воспроизведения и вычисления монотонной функции, выходной код NYсчетчика 1 функции будет соответствовать числу импульсов, равному
(21) К моменту окончания длительности Т, соответствующему концу цикла воспроизведения и вычисления монотонной функции, выходной код NYсчетчика 1 функции будет соответствовать числу импульсов, равному
NY= A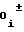 Ni (22) причем, в силу плавности воспроизведения, характеризуемого отсутствием записи каких-либо чисел в этот счетчик в моменты прохождения узлов аппроксимации, что приводило бы к скачкообразному изменению (разрыву) его выходного кода, будут справедливы с учетом формул (11) и (13) равенства, соответствующие условию непрерывности функции воспроизведения (11) либо (2) согласно выражениям (5), (7) либо (6), (8)
Ni (22) причем, в силу плавности воспроизведения, характеризуемого отсутствием записи каких-либо чисел в этот счетчик в моменты прохождения узлов аппроксимации, что приводило бы к скачкообразному изменению (разрыву) его выходного кода, будут справедливы с учетом формул (11) и (13) равенства, соответствующие условию непрерывности функции воспроизведения (11) либо (2) согласно выражениям (5), (7) либо (6), (8)
A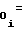 A
A Ni-1 (23)
Ni-1 (23)
Ni-1= 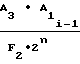 ΔF1 ±
ΔF1 ± 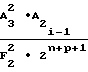 ΔF
ΔF
Ni-1= 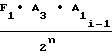 ΔT2 ±
ΔT2 ± 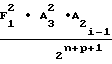 ΔT
ΔT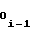 ,A
,A - выходные коды счетчика i функции, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках. Знаки полярности "+" либо "-" в выражениях (22) и (23) употребляются в зависимости от режима, в котором должен работать счетчик 1 функции - в суммирующем, либо в вычитающем соответственно, при этом выходной код счетчика 1 функции в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A
- выходные коды счетчика i функции, соответствующие начальным моментам аппроксимации на i-1-ом и i-ом участках. Знаки полярности "+" либо "-" в выражениях (22) и (23) употребляются в зависимости от режима, в котором должен работать счетчик 1 функции - в суммирующем, либо в вычитающем соответственно, при этом выходной код счетчика 1 функции в начальный момент аппроксимации на первом участке соответствует записанной в него ранее начальной уставке A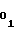 .
.
Учитывая выражения (20) и (21), формулу (22) запишем в виде
NY = A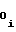 ±
± 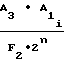
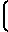 F1-F
F1-F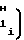 ±
±  ·
· 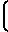 F1-F
F1-F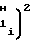 (26) либо в виде
(26) либо в виде
NY = A
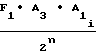 ·
· 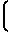 T2-T
T2-T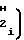 ±
± 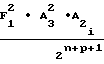 ·
· 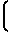 T2-T
T2-T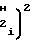 (27)
(27)
Полагая в формуле (26) F1 = Fx и сопоставляя ее с формулой (1), можно отметить, что при соблюдении равенств
a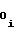 =
= 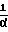 A
A (28) a
(28) a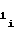 =
= 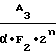 · A
· A (29)
(29)
a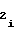 =
= 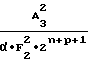 · A
· A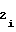 (30) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (1), аргумент которой представлен частотой
(30) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (1), аргумент которой представлен частотой
NY = α˙Y, (31) где α- коэффициент масштабирования.
Полагая в формуле (27) T2 = Tx = 1/Fx и сопоставляя ее с формулой (2), можно отметить, что при соблюдении равенств
b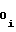 =
= 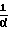 · A
· A (32) b
(32) b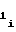 =
= 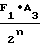 · A
· A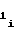 (33)
(33)
b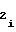 =
= 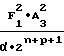 · A
· A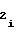 (34) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (2), аргумент которой представлен периодом частоты.
(34) будет выполняться соотношение, выражающее прямо пропорциональную зависимость выходного кода NY счетчика 1 функции от значения функции воспроизведения (2), аргумент которой представлен периодом частоты.
Для удобства отсчета результата вычисления счетчик 1 функции может быть выполнен двоично-десятичным, а коэффициент αвыбран кратным десяти.
Соблюдение равенств (28) либо (32) при заданномα обеспечивается путем выбора величины начальной уставки A , соответствующей коэффициенту a
, соответствующей коэффициенту a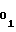 либо b
либо b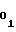 первого участка аппроксимации, и выполнения равенств (29), (30) либо (33), (34) для каждого из m участков, необходимость выполнения которых вытекает из формул (5)...(8) и (23)...(25).
первого участка аппроксимации, и выполнения равенств (29), (30) либо (33), (34) для каждого из m участков, необходимость выполнения которых вытекает из формул (5)...(8) и (23)...(25).
В свою очередь соблюдение равенств (29) либо (33) при заданных α, n, A3, F2 либо F1 обеспечивается путем выбора величины начальной уставки A , соответствующей коэффициенту a
, соответствующей коэффициенту a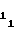 либо b
либо b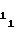 первого участка аппроксимации, и выполнения для последующих участков определенного соотношения между значением коэффициента a
первого участка аппроксимации, и выполнения для последующих участков определенного соотношения между значением коэффициента a либо b
либо b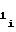 i-го участка и значениями коэффициентов a
i-го участка и значениями коэффициентов a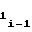 и a
и a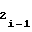 либо b
либо b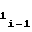 и b
и b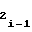 i-1-го участка, которое сводится к следующему.
i-1-го участка, которое сводится к следующему.
Учитывая равенства (11), (17) и (29), формулу (16) запишем в виде
a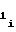 = a
= a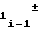
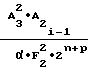 ΔF1 (35)
ΔF1 (35)
Используя равенство (30), для случая ΔF1 = ΔFx получаем соотношение
a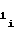 = a
= a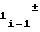 2 · a2i-1ΔFx (36) т.е. при разбиении на участки диапазона изменения частоты Fx аргумента значение коэффициента a
2 · a2i-1ΔFx (36) т.е. при разбиении на участки диапазона изменения частоты Fx аргумента значение коэффициента a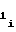 i-го участка должно определяться по значениям коэффициентов a
i-го участка должно определяться по значениям коэффициентов a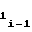 и a
и a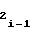 предшествующего i-1-го участка. При этом нетрудно убедиться, что соблюдение соотношения (36) равносильно необходимости соблюдения в узлах аппроксимации непрерывности первой производной функции воспроизведения (1) при разбиении ее на участки, т.е. необходимости выполнения равенства
предшествующего i-1-го участка. При этом нетрудно убедиться, что соблюдение соотношения (36) равносильно необходимости соблюдения в узлах аппроксимации непрерывности первой производной функции воспроизведения (1) при разбиении ее на участки, т.е. необходимости выполнения равенства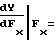
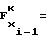
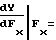
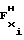 (37)
(37)
Для случая ΔT2 = ΔTx имеет место аналогичное равенство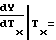
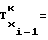
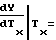
 (38)
(38)
Таким образом разбиение на участки диапазона изменения частоты Fxлибо периода Tx аргумента должно производиться при условии отсутствия в узлах аппроксимации разрыва не только функции воспроизведения (1) либо (2), но и ее первой производной, т.е. вышеуказанное разбиение должно осуществляться путем сплайн-аппроксимации полиномами второй степени.
Что касается соблюдения равенств (30) либо (34) при заданных α, n, p, A3, F2 либо F1, то оно обеспечивается установлением числа A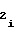 на входе ПКЧ 6 в начальный момент аппроксимации i-го участка, что достигается следующим образом. В момент начала формирования интервала времени Т импульсы с частотой F1 начинают поступать с выхода ключа 9 на вход предварительно обнуленного (цепь сброса на чертеже не показана) счетчика 7 длины участка, период Тп повторения выходных импульсов которого равен
на входе ПКЧ 6 в начальный момент аппроксимации i-го участка, что достигается следующим образом. В момент начала формирования интервала времени Т импульсы с частотой F1 начинают поступать с выхода ключа 9 на вход предварительно обнуленного (цепь сброса на чертеже не показана) счетчика 7 длины участка, период Тп повторения выходных импульсов которого равен
Tп= 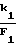 (39) где k1 - коэффициент пересчета счетчика 7 длины участка. Период Тп выбирается таким, чтобы он был равен времени преобразования ΔТ длины участка ΔF1 либо ΔT2, т.е. чтобы выполнялись равенства
(39) где k1 - коэффициент пересчета счетчика 7 длины участка. Период Тп выбирается таким, чтобы он был равен времени преобразования ΔТ длины участка ΔF1 либо ΔT2, т.е. чтобы выполнялись равенства
k1= 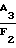 ΔF1 (40) либо
ΔF1 (40) либо
k1 = A3 ˙F1 ΔT2 (41) Выходные импульсы счетчика 7 длины участка с периодом Тп поступают на вход счетчика 8 номера участка, в результате чего последний поочередно устанавливается в одно из m состояний, начиная со второго. Установка счетчика 8 номера участка в первое состояние, соответствующее первому участку, и, тем самым, дальнейшее установление соответствия между номерами участков и состояниями счетчика 8 номера участка, производится путем подачи импульса обнуления (цепь сброса на чертеже не показана) в тот же момент, что и для счетчика 7 длины участка, а, именно, перед открытием ключа 9, например, в момент записи начальных уставок A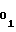 и A
и A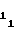 . Последовательно сменяемая по мере перехода с участка на участок кодовая комбинация с выходных шин счетчика 8 номера участка поступает на управляющие входы мультиплексора 5, в результате чего на выходе последнего в моменты перехода с i-1-го на i-ый участок устанавливается необходимое i-му участку число A
. Последовательно сменяемая по мере перехода с участка на участок кодовая комбинация с выходных шин счетчика 8 номера участка поступает на управляющие входы мультиплексора 5, в результате чего на выходе последнего в моменты перехода с i-1-го на i-ый участок устанавливается необходимое i-му участку число A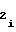 из ряда мультиплексируемых с четвертого 18 установочного входа чисел A
из ряда мультиплексируемых с четвертого 18 установочного входа чисел A ... A
... A , шины которых соединены с информационными входами мультиплексора 5. Установление необходимых чисел A
, шины которых соединены с информационными входами мультиплексора 5. Установление необходимых чисел A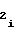 на входе ПКЧ 6 может производиться не только с помощью мультиплексора 5, но и с помощью, например, дешифратора, преобразователя кода на программируемой логической матрице или ПЗУ, в котором заранее "прошиты" вышеуказанные числа. При этом для каждого из заменяющих элементов входным кодом (для ПЗУ - адресным), как и для мультиплексора 5, является код выходных шин счетчика 8 номера участка, а их выходным кодом - код чисел A
на входе ПКЧ 6 может производиться не только с помощью мультиплексора 5, но и с помощью, например, дешифратора, преобразователя кода на программируемой логической матрице или ПЗУ, в котором заранее "прошиты" вышеуказанные числа. При этом для каждого из заменяющих элементов входным кодом (для ПЗУ - адресным), как и для мультиплексора 5, является код выходных шин счетчика 8 номера участка, а их выходным кодом - код чисел A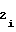 , полученный в результате операции дешифрирования, преобразования или выборки.
, полученный в результате операции дешифрирования, преобразования или выборки.
Таким образом реализация сплайн-аппроксимации функции воспроизведения (1) либо (2) сводится к установлению в счетчиках 1 и 2 начальных уставок A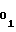 и A
и A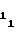 , соответствующих первому участку аппроксимации, и установлению с помощью мультиплексора 5 на кодовом входе ПКЧ 6 числа A
, соответствующих первому участку аппроксимации, и установлению с помощью мультиплексора 5 на кодовом входе ПКЧ 6 числа A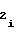 , соответствующего i-му участку, начиная с первого. При этом нет необходимости в начале каждого из последующих участков производить запись в счетчиках 1 и 2 чисел A
, соответствующего i-му участку, начиная с первого. При этом нет необходимости в начале каждого из последующих участков производить запись в счетчиках 1 и 2 чисел A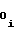 и A
и A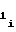 , так как эти числа на кодовых выходах указанных счетчиков устанавливаются автоматически в силу непрерывного (без скачков) ими счета импульсов, соответствующего непрерывности функции воспроизведения (1) либо (2) и ее первой производной, что, как отмечалось выше, характерно для сплайн-аппроксимации.
, так как эти числа на кодовых выходах указанных счетчиков устанавливаются автоматически в силу непрерывного (без скачков) ими счета импульсов, соответствующего непрерывности функции воспроизведения (1) либо (2) и ее первой производной, что, как отмечалось выше, характерно для сплайн-аппроксимации.
Кодовая уставка A3, максимальное значение которой равно объему второго счетчика 10 импульсов, выбирается исходя из требуемого значения длительности цикла воспроизведения согласно формуле (9).
Упоминаемые ранее режимы работы счетчиков 1 и 2 на сложение либо на вычитание устанавливаются заранее, исходя из знаков полярности производных функции воспроизведения (1) либо (2), а, именно:
если знак полярности первой производной на любом без исключения i-ом участке положителен, т.е. если функция воспроизведения (1) либо (2) монотонно возрастающая, то счетчик 1 функции необходимо устанавливать в режим сложения, а если отрицателен, то в режим вычитания;
если полярность произведения знаков полярности первой и второй производных на любом без исключения i-ом участке положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
Учитывая, что в аппроксиматоре рассматривается функция воспроизведения (1) либо (2), у которой полярность первой и второй производных неизменна во всем диапазоне изменения частоты Fx либо периода Tx аргумента, в том числе и при Fx= F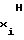 либо Tx=T
либо Tx=T , учет знаков полярности вышеуказанных производных при выборе режимов работы счетчиков 1 и 2 можно заменить на более простой учет знаков полярности перед коэффициентами a
, учет знаков полярности вышеуказанных производных при выборе режимов работы счетчиков 1 и 2 можно заменить на более простой учет знаков полярности перед коэффициентами a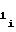 и a
и a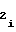 либо b
либо b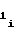 и b
и b , каждый из которых, как указывалось выше, одинаков для каждого из m участков, а, именно:
, каждый из которых, как указывалось выше, одинаков для каждого из m участков, а, именно:
если перед коэффициентом a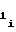 либо b
либо b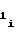 знак "+", то счетчик 1 функции необходимо устанавливать в режим сложения, а если знак "-", то в режим вычитания;
знак "+", то счетчик 1 функции необходимо устанавливать в режим сложения, а если знак "-", то в режим вычитания;
если полярность произведения знаков полярности перед коэффициентами a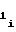 и a
и a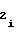 либо b
либо b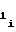 и b
и b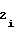 положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
положительна, то счетчик 2 импульсов необходимо устанавливать в режим сложения, а если отрицательна, то в режим вычитания.
Необходимо подчеркнуть, что, в силу одинаковости знаков полярности перед одноименными коэффициентами функции воспроизведения (1) либо (2) на каждом из m ее участков, режимы работы счетчиков 1 и 2 на сложение либо на вычитание, заранее устанавливаемые согласно вышеуказанным знакам, также одинаковы на каждом из этих участков.
Следует отметить, что если функция воспроизведения (1) либо (2) представлена в более краткой форме
Y = c c
c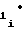 Fx ± c
Fx ± c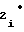 F
F
Y = d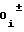 d
d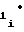 Tx± d
Tx± d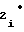 T
T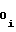 ,c
,c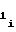 ,c
,c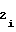 - постоянные коэффициенты, d
- постоянные коэффициенты, d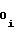 ,d
,d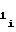 ,d
,d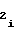 . то связь между приведенными коэффициентами и коэффициентами a
. то связь между приведенными коэффициентами и коэффициентами a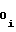 ,a
,a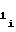 ,a
,a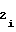 ,b
,b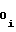 ,b
,b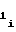 и b
и b можно выразить соотношениями
можно выразить соотношениями
c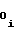 = a
= a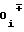 a
a F
F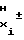 a
a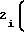 F
F (44)
(44)
c = a
= a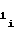 -2 · a
-2 · a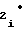 F
F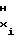 (45)
(45)
c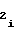 = a
= a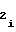 (46) либо
(46) либо
d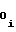 = b
= b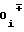 b
b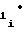 T
T b
b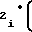 T
T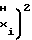 (47)
(47)
d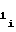 = b
= b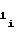 -2 · b
-2 · b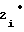 T
T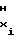 (48)
(48)
d = b
= b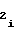 (49) Учитывая прямо пропорциональную зависимость длительности Т интервала времени от частоты Fx либо периода Tx аргумента, можно отметить, что на первом участке при T = 0 частота аргумента F
(49) Учитывая прямо пропорциональную зависимость длительности Т интервала времени от частоты Fx либо периода Tx аргумента, можно отметить, что на первом участке при T = 0 частота аргумента F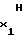 = 0 либо период частоты T
= 0 либо период частоты T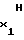 = 0. При этом выражения (44)...(49) для первого участка примут вид
= 0. При этом выражения (44)...(49) для первого участка примут вид
c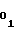 = a
= a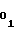 (50) c
(50) c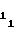 = a
= a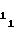 (51) c
(51) c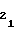 = a
= a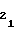 (52) либо
(52) либо
d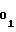 = b
= b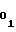 (53) d
(53) d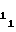 = b
= b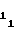 (54) d
(54) d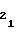 = b
= b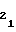 (55) т.е. для первого участка имеет место идентичность рассматриваемых коэффициентов, согласно которым, как указывалось выше, устанавливаются начальные уставки A
(55) т.е. для первого участка имеет место идентичность рассматриваемых коэффициентов, согласно которым, как указывалось выше, устанавливаются начальные уставки A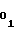 , A
, A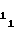 и число A
и число A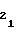 .
.
Таким образом, благодаря новым связям, элементам и возможности установки различного сочетания режимов работы счетчиков 1 и 2, обеспечивается с учетом масштабирования аппаратурная реализация воспроизведения и вычисления монотонных функций, как возрастающих, так и убывающих, выпуклых как вверх, так и вниз (в зависимости от знака полярности перед коэффициентом a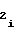 либо b
либо b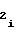 ), воспроизводимых путем сплайн-аппроксимации, и аргумент которых может быть представлен частотой либо ее периодом. Кроме того повышается точность воспроизведения функции за счет реализации кусочно-квадратичной аппроксимации, как более точной по сравнению с кусочно-линейной, применяемой в прототипе.
), воспроизводимых путем сплайн-аппроксимации, и аргумент которых может быть представлен частотой либо ее периодом. Кроме того повышается точность воспроизведения функции за счет реализации кусочно-квадратичной аппроксимации, как более точной по сравнению с кусочно-линейной, применяемой в прототипе.
| название | год | авторы | номер документа |
|---|---|---|---|
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2023296C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2023297C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2018948C1 |
| АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ | 1991 |
|
RU2018947C1 |
| Устройство для измерения температуры | 1990 |
|
SU1809328A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721606A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721604A1 |
| Устройство для воспроизведения квадратичных функций | 1989 |
|
SU1721605A1 |
| Устройство для измерения температуры | 1988 |
|
SU1642270A1 |
| Генератор импульсов параболической формы | 1989 |
|
SU1721803A1 |
Изобретение относится к автоматике и вычислительной технике и может найти применение в специализированных вычислительных и информационно-измерительных системах. Целью изобретения является повышение точности за счет реализации кусочно-квадратичной зависимости. Аппроксиматор содержит счетчик длины участка, счетчик функции, преобразователь кода в частоту, первый и второй счетчики импульсов, счетчик номера участка, два ключа и управляемый делитель частоты, который выполнен в виде последовательно соединенных кодовыми шинами мультиплексора и преобразователя кода в частоту. Это позволило расширить класс решаемых задач, воспроизводя как монотонно возрастающие, так и монотонно убывающие функции,аргумент которых может быть представлен как частотой, так и ее периодом. 1 ил.
АППРОКСИМАТОР МОНОТОННЫХ ФУНКЦИЙ, содержащий счетчик длины участка и первый ключ, причем счетный вход счетчика длины участка соединен с выходом первого ключа, отличающийся тем, что, с целью повышения точности путем реализации кусочно-квадратичной зависимости, он содержит второй ключ, два счетчика импульсов, преобразователь кода в частоту, счетчик функции, счетчик номера участка и управляемый делитель частоты, причем первый вход аргумента аппроксиматора соединен с информационным входом первого ключа, выход которого соединен с частотными входами управляемого делителя частоты и преобразователя кода в частоту, выход которого соединен со счетным входом счетчика функции, информационный вход и выход которого соединены соответственно с первым установочным входом и выходом аппроксиматора, второй установочный вход которого соединен с информационным входом первого счетчика импульсов, выход и счетный вход которого соединены соответственно с информационным входом преобразователя кода в частоту и выходом управляемого делителя частоты, информационный и управляющий входы которого соединены соответственно с третьим установочным входом аппроксиматора и выходом счетчика номера участка, счетный вход которого соединен с выходом счетчика длины участка, вход запуска аппроксиматора соединен с управляющими входами первого и второго ключей, блокировочные входы которых соединены с выходом второго счетчика импульсов, информационный и счетный входы которого соединены соответственно с четвертым установочным входом аппроксиматора и выходом второго ключа, информационный вход которого соединен с вторым входом аргумента аппроксиматора.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Функциональный частотный преобразователь | 1980 |
|
SU947870A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1994-11-15—Публикация
1991-06-28—Подача