Изобретение относится к технике дискретного спектрального анализа и может быть использовано в радиолокации и измерительной технике.
Известен способ определения частоты сигнала переменного тока, в котором определяются моменты перехода мгновенного значения входного сигнала через нуль, подсчитывается число N периодов сигнала между первым и n-ым переходом через нуль, число Ns интервалов выборок между первым и n-ым переходом через нуль, запоминаются амплитуды a1, a2, a3, a4 сигнала непосредственно перед первым переходом через нуль, и вычисляется значение частоты по формуле
F = 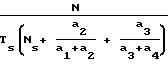 где Тs - период выборок.
где Тs - период выборок.
Недостатком указанного способа является малый диапазон определения частоты сигнала переменного тока, верхнее значение которого не может превышать половины частоты следования выборок fв≅1/(2Ts).
Известен также способ определения частоты путем дискретизации входного сигнала с получением N точек, вычисления дискретного спектра с помощью дискретного преобразования Фурье (ДПФ), поиска номера F максимальной спектральной составляющей и вычислении значения частоты по формуле fo=F Δf, где Δf=1/T - дискретность спектра;
Т - интервал наблюдения сигнала.
Недостатком данного способа является малый диапазон однозначного определения частоты, верхнее значение которого не может превышать половины значения частоты дискретизации fв=N Δf/2.
Наиболее близким к изобретению является способ определения частоты путем одновременной дискретизации входного сигнала с получением N и N-1 точки, определения номера максимальных составляющих спектров, полученных с помощью ДПФ, сопоставления и точечных дискретных спектров и нахождения истинной частоты в точке, где максимумы периодических спектров совпадают.
Сущность данного способа состоит в следующем.
Значения частоты по каждому спектру в отдельности определяется согласно выражениями fo= (K1+e1V) Δf и fo=[K1+e1(N-1)] Δf, (1) где K1 и К2 - номера максимальных спектральных составляющих N и N-1 точечных дискретных спектров соответственно;
e1 и e2 - номера периодов дискретных спектров для N и N-1 точечных ДПФ соответственно.
После вычисления ДПФ получают дискретные спектры и определяют номера максимальных составляющих спектра, которые для N и N-1 точечных ДПФ изменяются в пределах К1=0,1,...,N-1 и K2=0,1,...,N-2. Значение частоты входного сигнала в соответствии с формулой изобретения, определяется из выражения
fo= Δf 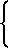
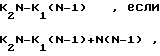
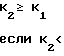
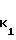
Недостатком данного способа является то, что однозначное определение частоты возможно только в том случае, когда в результате дискретизации формируется последовательность комплексных отсчетов входного сигнала. Это обусловлено тем, что выражения (1) справедливы только для случая, когда в результате дискретизации формируется комплексная последовательность отсчетов входного сигнала.
Целью изобретения является расширение диапазона однозначного определения частоты за счет исключения в нем областей неправильного определения частоты.
Поставленная цель достигается тем, что в способе определения частоты, заключающемся в получении одновременно N-1 и N дискретных значений входного сигнала, определении номера максимальных спектральных составляющих, полученных с помощью дискретного преобразования Фурье, предусмотрено одновременно производить дискретизацию входного сигнала с получением N+1 точек, определение номера максимальной спектральной составляющей из вновь полученного спектра с помощью ДПФ и по полученным номерам максимальных спектральных составляющих, определение возможного формирования значения частоты входного сигнала в соответствии с формулами
F1 = |K1N - K2 ( N - 1) |; (3)
F2 = K1N + K2 (N - 1);
F3 = N (N - 1) - F1;
F4 = N (N - 1) - F2 ;
F5 = | K2 ( N + 1) - K3N |;
F6 = K2 ( N + 1) + K3N ;
F7 = N ( N + 1 ) - F5 ;
F8 = N ( N + 1) - F6 ;
где К1, К2 и К3 - номера максимальных спектральных составляющих N-1, N и N+1 точечных дискретных спектров соответственно;
N - количество точек ДПФ.
При этом в качестве истинного нормированного значения частоты Foвыбирается значение, при котором выполняется равенство
Fo=Fi=Fj, где i=1,2,3,4 ,
j= 5,6,7,8, а абсолютное значение частоты входного сигнала рассчитывается по формуле
fo=Fo Δf, где Δf=1/Т - дискретность спектра;
Т - интервал рассмотрения входного сигнала.
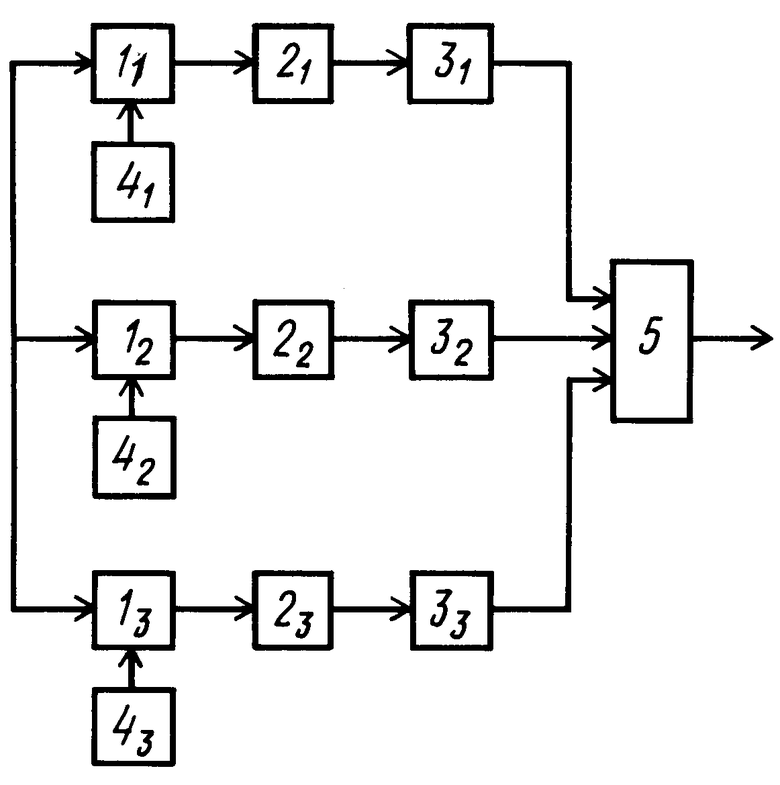
На чертеже приведена блок-схема устройства, реализующая предлагаемый способ.
Сущность изобретения заключается в следующем. Одновременно производят дискретизацию входного сигнала с получением N-1, N и N+1 точки, определяют номера максимальных составляющих спектров, полученных с помощью ДПФ, и по этим номерам определяют возможные нормированные значения частоты входного сигнала в соответствии с формулами
F1 = |K1N - K2 ( N - 1) |;
F2 = K1N + K2 (N - 1);
F3 = N (N - 1) - F1;
F4 = N (N - 1) - F2 ;
F5 = |K2 ( N + 1) - K3N | ;
F6 = K2 ( N + 1) + K3N ;
F7 = N ( N + 1 ) - F5 ;
F8 = N ( N + 1) - F6 ; при этом в качестве истинного нормированного значения частоты Fo выбирается значение, при котором выполняется равенство
Fo=Fi=Fj, а абсолютное значение частоты входного сигнала рассчитывается по формуле
fo=Fo= Δ f.
Устройство содержит аналого-цифровые преобразователи (АЦП) 11, 12 и 13; блоки 21, 22 и 23 ДПФ; блоки 31, 32 и 33 поиска номера максимальной спектральной составляющей; генераторы 41, 42 и 43, блок 5 определения частоты.
Элементы устройства, реализующего предлагаемый способ, соединены следующим образом. Входом устройства являются объединенные входы АЦП 11, 12 и 13, выходы которых соединены соответственно с входами блоков 21, 22и 23 ДПФ, выходы последних соединены соответственно с входами блоков 31, 32 и 33 поиска номера максимальной спектральной составляющей. Выходы блоков 31, 32 и 33 соединены с входами блока 5 определения частоты. Выходы генераторов 41, 42 и 43 соединены с тактовыми входами соответствующих АЦП 11, 12 и 13.
Предлагаемая блок-схема устройства определения частоты получена в результате усовершенствования известного устройства определения частоты. В состав устройства входит два АЦП, два блока ДПФ и два блока поиска номера максимальной спектральной составляющей и блок определения частоты, за счет чего расширяется диапазон однозначного определения частоты. Однако в данном устройстве имеются области частот D1 и D2, где
[i(N-1)-N/2+1]Δf ≅ D1≅ [iN-1]Δf,i=1,2,..., N/2 и
[(N/2+i)N-3N/2+1] Δf≅D2≅[(N/2+i(N-t)-1]Δf,i=1,2,...,N/2, в которых частота входного сигнала определяется неправильно. Введение третьего АЦП/ третьего блока ДПФ и третьего блока поиска номера максимальной спектральной составляющей позволяет исключить области неправильного определения частоты входного сигнала и тем самым расширить диапазон однозначного определения частот известного устройства определения частот.
Устройство работает следующим образом.
Входной сигнал дискретизируется в АЦП 11, 12 и 13 с частотой (N-1) Δ f, NΔf и (N+1) Δ f соответственно. Частота дискретизации задается генераторами 41, 42 и 43. При этом на одной реализации входного сигнала получают соответственно N-1, N и N+1 отсчетов, которые поступают на входы блоков 21, 22 и 23 ДПФ соответственно, где вычисляются дискретные спектры. В блоках 31, 32 и 33 определяются номера максимальных спектральных составляющих К1, К2 и К3 соответственно, которые поступают на блок 5 определения частоты.
Так как на входах АЦП 11, 12 и 13 формируется последовательность действительных отсчетов входного сигнала, то их ДПФ обладает свойством симметрии. В этом случае диапазон однозначного определения частоты для каждого в отдельности дискретного спектра не превышает половины частоты дискретизации. Номера максимальных спектральных составляющих N-1, N и N+1 точечных ДПФ соответственно определяются значениями: К1 и N-1-K1; K2и N-К2; К3 и N+1-К3. При этом значения коэффициентов К1, К2 и К3 могут принимать значения в диапазоне: 0 ≅K1 ≅N/2 -1, 0 ≅ K2 ≅N/2 и 0≅ K3 ≅ N/2. Номера максимальных спектральных составляющих для других периодов N-1, N и N+1 точечных ДПФ определяются соответственно из выражений e1(N-1)+K1 и (e1+1)(N+1)-K1; e2N+K2 и (e2+1)N-K2; e3(N+1)+K3 и (e3+1)(N+1)-K3.
Запишем выражения для определения частоты по каждому спектру в отдельности
fo= 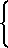
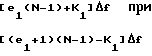
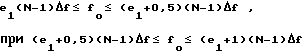

fo= 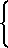
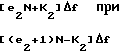
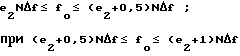

fo= 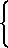
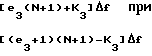
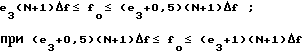

Перейдем к относительной частоте F=fo/ Δf, тогда
F = 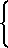
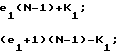
(1)
F = 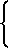
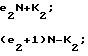
(2)
F = 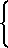
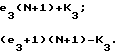
(3)
Так как в блоках 31, 32 и 33 поиска номера максимальных спектральных составляющих определяются соответственно только номера К1, К2 и К3, а коэффициенты e1, e2 и e3 неизвестны, то при определении частоты по каждому дискретному спектру в отдельности возникает неоднозначность определения частоты. При этом в каждом из выражений (1)-(3) только одно значение частоты является истинным. Для исключения неоднозначности определение значения частоты будем производить совместно по двум дискретным спектрам. Рассмотрим первоначально определение частоты по N-1 и N точечным дискретным спектрам. Так как N-1< N , то e1≥e2, тогда e1=e2+ Х1, где Х1=0,1,2,...
Подставляя значения e1 в (1), получим
F = 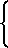
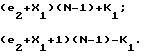
Откуда
e2= 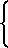
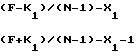
Подставляя поочередно первое и второе значения e2 в первое и второе уравнение (2), получим
F = 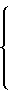
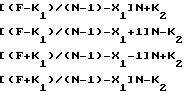
Умножая обе части равенств на -(N-1) и перенося из правой части в левую слагаемое NF, получим
F = 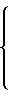
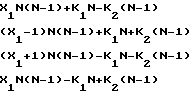 (4)
(4)
Если диапазон однозначного определения частоты ограничить значением 0≅F≅N(N-1), то Х1 принимает только два значения 0 или 1. В этом случае система уравнений (4) преобразуется к виду
F = 
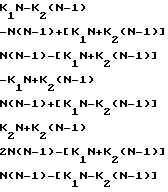



(5)
Поскольку 0≅K1≅N/2-1, а 0≅K2≅N /2, то второе уравнение в (5) принимает всегда отрицательное значение, а седьмое уравнение - значение большее N(N-1), что выходит за границы диапазона однозначного определения частот. Следовательно, второе и седьмое уравнения можно исключить из системы уравнений (5).
Первое и четвертое уравнения в (5) принимают одинаковые по модулю значения, а их знаки противоположны. Поэтому первое и четвертое уравнения в (5) сложно объединить в виде F=| K1N-K2(N-1) |, при этом устраняется неправильный результат в виде отрицательного значения частоты входного сигнала.
Пятое и восьмое уравнения в (5) содержат одинаковые слагаемые, выделенные квадратными скобами, которые отличаются знаком. Если выражение в квадратных скобках принимает положительное значение, то пятое уравнение принимает всегда значение больше N(N-1).
Если выражение в квадратных скобках принимает отрицательное значение, то восьмое уравнение также принимает значение, большее N(N-1), что выходит за границы области однозначного определения частоты. Поэтому пятое и восьмое уравнения в (5) можно объединить в виде
F=N(N-1)- | K1N-K2(N-1) |
C учетом изложенного выше система уравнений (5) приобретает вид
F1 = |K1N - K2 (N - 1)|
F2 = K1N + K2 (N - 1)
F3 = N (N - 1) - F1 (6)
F4 = N (N - 1) - F2
Для уменьшения объема вычислений систему уравнений (6) можно преобразовать к виду F = 
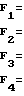
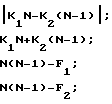 (7)
(7)
Система уравнений (7) позволяет рассчитать 4 значения частоты входного сигнала и только одно из них является истинным. По сравнению с выражением (2) количество неоднозначных значений частоты существенно уменьшилось.
Для дальнейшего исключения неоднозначности определим значения частоты совместно по N и N+1 точечным дискретным спектрам. Так как N< N + 1, то e2 ≥ e3, тогда e2=e3+X2, где Х=0,1,2,...,. Подставляя значения e2 в (2), получим
F = 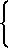
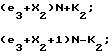
откуда
e3= 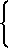
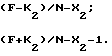
Подставляя поочередно первое и второе значения e3 в первое и второе уравнение (3), получим
F = 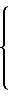
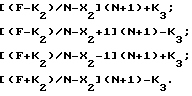
Умножая обе части равенств на -N и перенося из правой части в левую слагаемое -(N+1)F, получим
F = 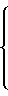
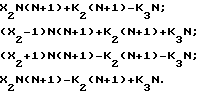 (8)
(8)
Если диапазон однозначного определения частоты ограничить значением 0≅F≅N (N-1), то Х2 принимает, также как и Х1, только два значения 0 или 1. В этом случае система уравнений (8) преобразуется к виду
F = 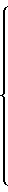
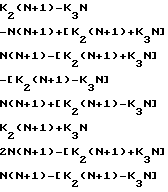



(9)
Поскольку 0 ≅K2≅N/2, а 0≅K3≅N /2, то второе уравнение в (9) принимает всегда отрицательное значение, а седьмое уравнение - значение, большее N(N+1), что выходит за границы диапазона однозначного определения частот. Следовательно, второе и седьмое уравнения можно исключить из системы уравнений (9).
Первое и четвертое уравнения в (9) принимают одинаковые по модулю значения, а их знаки противоположны. Поэтому первое и четвертое уравнения в (9) можно объединить в виде F=|K2(N+1)-K3N|, при этом устраняется неправильный результат в виде отрицательного значения частоты входного сигнала.
Пятое и восьмое уравнения в (9) содержат одинаковые слагаемые, выделенные квадратными скобками, которые отличаются знаком. Если выражение в квадратных скобках принимает положительное значение, то пятое уравнение в (9) всегда принимает значение, большее N(N-1). Если выражение в квадратных скобках принимает отрицательное значение, то восьмое уравнение в (9) всегда принимает значение, большее N(N-1), что выходит за границы диапазона однозначного определения частоты. Поэтому пятое и восьмое уравнения в (9) можно объединить в виде F=N(N+1)- |K2(N+1)-K3N | .
C учетом изложенного выше система уравнений (9) принимает вид
F = 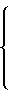
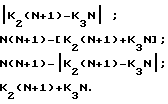 (10)
(10)
Для уменьшения объема вычислений систему уравнений (10) можно преобразовать к виду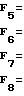
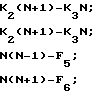 (11)
(11)
Система уравнений (11) позволяет рассчитать 4 значения частоты входного сигнала, одно из которых, как и в (7), является истинным.
В блоке 5 определения частоты по найденным значениям номеров К1, К2и К3 максимальных спектральных составляющих рассчитываются значения частот F1, F2, . . . , F8 в соответствии с (8) и (11). Затем производится перекрестное сравнение значений частот Fi и Fj, где i=1,2,3,4; j=5,6,7,8. Одно из значений Fi и одно из значений Fj являются истинными, следовательно, их численные значения равны между собой. Тогда истинным значением Fo будет значение, при котором выполняется равенство Fo= Fi= Fj, где i=1,2,3,4; j= 5,6,7,8.
Абсолютное значение частоты входного сигнала определяется из выражения fo=Fo Δf; где Fo=Fi=Fj при i=1,2,3,4 и j=5,6,7,8;
Δ f - дискретность спектра.
Технико-экономический эффект предлагаемого способа определения частоты заключается в расширении диапазона однозначного определения частот за счет исключения в нем областей неправильного определения частоты.
Области D1 и D2 неправильного определения частоты в прототипе определяется значением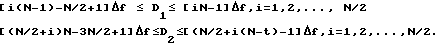
Определим, во сколько раз суммарная область неправильного определения частоты больше суммарной области правильного определения частоты. В диапазоне частот 0≅f<N /2(N-1) Δf.
i-ю область неправильного определения частот можно найти как разность верхней и нижней граничных частот областей
ΔDi= [iN+1]Δf-[i(N-1)-N/2+1]Δf = [i+N/2-2]Δf.
Поскольку таких областей насчитывается N/2, то суммарная их ширина в диапазоне частот 0≅f<N/2(N-1) Δf равна D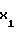 =
= 
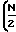 - 2
- 2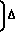 f+
f+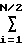 iΔf Учитывая равенство
iΔf Учитывая равенство 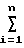 i =
i = 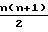 , данное равенство можно преобразовать к виду D
, данное равенство можно преобразовать к виду D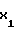 =
= 
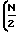 - 2
- 2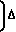 f+
f+ 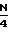
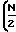 + 1
+ 1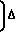 f =
f = 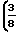 N2-
N2- 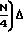 f ≈
f ≈  N2Δf Ширина диапазона частот 0≅ f<
N2Δf Ширина диапазона частот 0≅ f<  (N+1)Δf составляет
(N+1)Δf составляет  (N-1)Δf ≈
(N-1)Δf ≈ 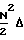 f. Следовательно, ширина суммарной области правильного определения частоты составляет
f. Следовательно, ширина суммарной области правильного определения частоты составляет
D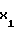 =
= 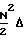 f-D
f-D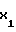 =
=  N2Δf
N2Δf
Таким образом, суммарная область неправильного определения частоты в диапазоне 0≅ f≅  (N-1)Δf больше суммарной области правильного определения частоты приблизительно в M =
(N-1)Δf больше суммарной области правильного определения частоты приблизительно в M = 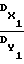 = 3 раза.
= 3 раза.
В диапазоне частот  (N-1)Δf< f≅ [N(N-1)]Δf i-я область неправильного определения частоты находится из выражения
(N-1)Δf< f≅ [N(N-1)]Δf i-я область неправильного определения частоты находится из выражения D
D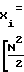
 (
( +
+ )
) N
N 1
1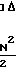 f
f [
[ 2
2 i
i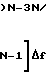 2
2 1
1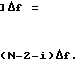
Поскольку таких областей насчитывается N/2, то суммарная их ширина в диапазоне частот N/2·(N-1)Δf<f≅N(N-1)Δf равна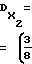
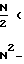 N
N 2
2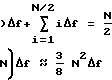 (N-2)Δf+
(N-2)Δf+ 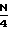
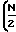 + 1
+ 1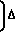 f =
f =
Ширина диапазона частот  (N-1)Δf< f≅ N(N-1)Δf составляет
(N-1)Δf< f≅ N(N-1)Δf составляет  (N-1)Δf ≈
(N-1)Δf ≈ 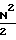 Δf . Следовательно, ширина суммарной области правильного определения частоты составляет D
Δf . Следовательно, ширина суммарной области правильного определения частоты составляет D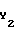 =
= 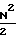 Δf-D
Δf-D =
=  N2Δf. Таким образом, суммарная область неправильного определения частот в диапазоне
N2Δf. Таким образом, суммарная область неправильного определения частот в диапазоне  (N-1)Δf< f≅ N(N-1)Δf больше суммарной области правильного определения частоты приблизительно в M =
(N-1)Δf< f≅ N(N-1)Δf больше суммарной области правильного определения частоты приблизительно в M = 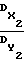 = 3 раза.
= 3 раза.
Таким образом, в известном способе определения частоты, выбранного в качестве прототипа, суммарная ширина области неправильного определения частоты в 3 раза больше суммарной ширины области правильного определения частоты. Исключение областей неправильного определения частот в предлагаемом способе определения частоты позволяет приблизительно в 3 раза расширить область однозначного определения частоты.
Использование предложенного способа позволит производить однозначное определение частоты в диапазоне частот 0≅f≅N/(N-1) Δ f, ширина которого в (N-2) раза превышает максимальную частоту дискретизации (N+1) Δf входного сигнала, используемую в данном способе.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения частоты | 1986 |
|
SU1352390A1 |
| Способ определения радиальной скорости объекта | 2020 |
|
RU2760104C1 |
| Способ определения частоты | 1988 |
|
SU1675793A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СПЕКТРА ЭЛЕКТРИЧЕСКОГО СИГНАЛА ПО ИЗМЕРЕННЫМ ВЫБОРОЧНЫМ ЗНАЧЕНИЯМ ЭТОГО СИГНАЛА | 2011 |
|
RU2475765C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2017162C1 |
| УСТРОЙСТВО ПОИСКА И СЛЕЖЕНИЯ ЗА ШИРОКОПОЛОСНЫМ СИГНАЛОМ | 1983 |
|
SU1840276A1 |
| СПОСОБ ОБНАРУЖЕНИЯ МНОЖЕСТВА УЗКОПОЛОСНЫХ РАДИОСИГНАЛОВ В ШИРОКОЙ ПОЛОСЕ ЧАСТОТ | 2010 |
|
RU2429494C1 |
| СПОСОБ АДАПТИВНОГО ПОДАВЛЕНИЯ ПОМЕХ | 2011 |
|
RU2456743C1 |
| Устройство для определения частоты | 1989 |
|
SU1698816A1 |
| СПОСОБ ИЗМЕРЕНИЯ ВНЕШНЕБАЛЛИСТИЧЕСКИХ ХАРАКТЕРИСТИК СНАРЯДА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2515580C1 |
Область использования в радиолокаци и измерительной технике. Сущность изобретения: заключается в одновременном получении N и N - 1 дискретных значений входного сигнала, определении номера максимальных спектральных составляющих, полученных с помощью дискретного преобразования фурье, отличительной особенностью которого является дополнительная дискретизация входного сигнала с получением N + 1 точек, определении номера максимальной спектральной составляющей вновь полученного спектра с помощью дискретного преобразования Фурье и вычислении по определенным формулам по полученным номерам максимальных спектральных составляющих абсолютного значения частоты входного сигнала. 1 ил.
СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТЫ, заключающийся в получении одновременно N и N - 1 дискретных значений входного сигнала, определении номера максимальных спектральных составляющих, полученных с помощью дискретного преобразования Фурье, отличающийся тем, что, с целью расширения диапазона однозначного определения частоты за счет исключения в нем областей неправильного определения частоты, одновременно производят дискретизацию входного сигнала с получением N + 1 точек, определяют номер максимальной спектральной составляющей из вновь полученного спектра с помощью дискретного преобразования Фурье и по полученным номерам максимальных спектральных составляющих определяют возможные нормированные значения частоты входного сигнала в соответствии с формулами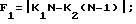
F2 = K1N + K2(N - 1);
F3 = N (N - 1) - F1;
F4 = N (N - 1) - F2;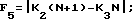
F6 = K2 (N + 1) + K3N;
F7 = N (N + 1) - F5;
F8 = N (N + 1) - F6,
где K1, K2, K3 - номера максимальных спектральных составляющих N - 1, N и N + 1 точечных дискретных спектров соответственно;
N - количество точек дискретного преобразования Фурье,
при этом в качестве истинного нормированного значения частоты выбирается значение, при котором выполняется равенство
F0 = Fi = Fj,
где i = 1,2,3,4;
j = 5,6,7,8,
а абсолютное значение частоты входного сигнала рассчитывается по формуле
fo=FoΔf,
где Δf=1/T - дискретность спектра;
T - интервал рассмотрения входного сигнала.
| Способ определения частоты | 1986 |
|
SU1352390A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1995-02-09—Публикация
1991-06-27—Подача