Изобретение относится к области радиоэлектроники, а именно к спектральному анализу электрических сигналов.
Определение спектра электрического сигнала (спектральный анализ) является актуальной задачей в области обработки и преобразования сигналов. Одним из подходов к решению этой задачи является определение спектра анализируемого сигнала по его временной выборке. По этому принципу реализуется дискретное преобразование Фурье (ДПФ), описанное, например, в [1] - прототип заявляемого способа.
Способ-прототип заключается в том, что анализируемый сигнал f(t) дискретизируют по времени с шагом дискретизации Т, преобразуют выборочные значения сигнала в цифровую форму с помощью аналого-цифрового преобразователя (АЦП) и определяют значения спектра сигнала, исходя из преобразования Фурье по формуле
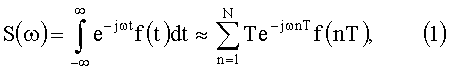
где n - номер шага дискретизации по времени, ω - круговая частота, N - длина временной выборки сигнала.
Определение спектральной составляющей по формуле (1) может выполняться для любых значений частоты ω, однако для цифровой реализации удобно определять спектр в дискретных точках оси частот, отстоящих одна от другой на постоянную величину - шаг дискретизации по частоте Ω. В этом случае выражение (1) приобретает вид
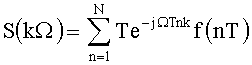
где k - номер шага дискретизации по частоте.
Способ-прототип имеет следующие недостатки. При определении спектра сигнала f(t) по формуле (1) необходимо обеспечить однозначное представление этого сигнала его временной выборкой f(nT). Согласно теореме Котельникова, для этого шаг дискретизации сигнала по времени должен удовлетворять условию 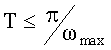 , где ωmax - максимальная частота спектра сигнала. На практике, согласно [2], это условие еще ужесточается, так что шаг дискретизации должен быть
, где ωmax - максимальная частота спектра сигнала. На практике, согласно [2], это условие еще ужесточается, так что шаг дискретизации должен быть 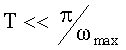 . Таким образом, чем выше частота анализируемого сигнала, тем меньший шаг дискретизации Т необходимо выбирать для выполнения этого условия и, соответственно, тем более быстродействующий и дорогой требуется АЦП, используемый для представления выборочных значений сигнала в цифровой форме. Как следствие, ДПФ имеет ограничение по частоте анализируемого сигнала. Кроме этого повышение частоты анализируемых сигналов сопровождается повышением стоимости анализаторов спектра из-за высоких требований к быстродействию АЦП.
. Таким образом, чем выше частота анализируемого сигнала, тем меньший шаг дискретизации Т необходимо выбирать для выполнения этого условия и, соответственно, тем более быстродействующий и дорогой требуется АЦП, используемый для представления выборочных значений сигнала в цифровой форме. Как следствие, ДПФ имеет ограничение по частоте анализируемого сигнала. Кроме этого повышение частоты анализируемых сигналов сопровождается повышением стоимости анализаторов спектра из-за высоких требований к быстродействию АЦП.
Технической задачей данного изобретения является создание способа определения спектра электрического сигнала по измеренным его выборочным значениям, полученным с произвольным шагом дискретизации по времени, не зависящим от частоты анализируемого сигнала, что позволяет расширить диапазон анализируемых частот в сторону их увеличения, а также снизить стоимость анализаторов спектра за счет применения в них менее быстродействующих, но более дешевых АЦП.
Поставленная задача достигается тем, что в способе определения спектра электрического сигнала, который заключается в дисретизации анализируемого сигнала по времени с шагом дискретизации T и измерении его дискретизированных выборочных значений путем преобразования их в цифровую форму, согласно изобретению, до проведения измерений интервал контролируемых частот (ωн, ωк), который включает спектр анализируемого сигнала, разбивают на элементы разрешения по частоте, размер которых Ω определяется требуемой точностью спектрального анализа, выбирают шаг дискретизации сигнала по времени исходя из удобства проведения измерений, формируют весовую матрицу W с компонентами 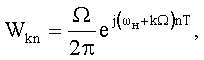 где k - номер элемента разрешения по частоте, n - номер измеренного выборочного значения сигнала, k=1, 2, …, К, n=1, 2, …, N, К - число элементов разрешения по частоте в интервале контролируемых частот, N - число измеренных выборочных значений анализируемого сигнала, измеренные выборочные значения анализируемого сигнала f(T)f(2T)…f(NT) объединяют в вектор
где k - номер элемента разрешения по частоте, n - номер измеренного выборочного значения сигнала, k=1, 2, …, К, n=1, 2, …, N, К - число элементов разрешения по частоте в интервале контролируемых частот, N - число измеренных выборочных значений анализируемого сигнала, измеренные выборочные значения анализируемого сигнала f(T)f(2T)…f(NT) объединяют в вектор 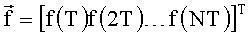 , где индекс Т обозначает транспонирование, составляют векторно-матричное уравнение измерений
, где индекс Т обозначает транспонирование, составляют векторно-матричное уравнение измерений 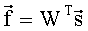 и определяют из него спектр анализируемого электрического сигнала в виде оценки спектрального вектора
и определяют из него спектр анализируемого электрического сигнала в виде оценки спектрального вектора  , компоненты которого представляют собой оценки днскретизированных по элементам разрешения составляющих спектра анализируемого сигнала.
, компоненты которого представляют собой оценки днскретизированных по элементам разрешения составляющих спектра анализируемого сигнала.
Поставленная задача решается за счет того, что вместо определения составляющих спектра сигнала исходя из прямого преобразования Фурье, как это делается в прототипе согласно (1), в заявляемом способе спектральные составляющие определяют исходя из обратного преобразования Фурье 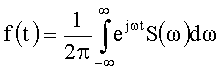 как дискретные значения подынтегральный функции S(ω). При этом определяющим оказывается шаг дискретизации по частоте Ω подынтегральной функции S(ω), а моменты измерений сигнала могут выбираться произвольно, аналогично тому, как в прототипе выражение (1) может быть вычислено для произвольного значения ω, но при достаточно малом шаге дискретизации по времени Т.
как дискретные значения подынтегральный функции S(ω). При этом определяющим оказывается шаг дискретизации по частоте Ω подынтегральной функции S(ω), а моменты измерений сигнала могут выбираться произвольно, аналогично тому, как в прототипе выражение (1) может быть вычислено для произвольного значения ω, но при достаточно малом шаге дискретизации по времени Т.
Особенностью предлагаемого способа является то, что выборочные значения сигнала могут измеряться в любые удобные для измерения моменты времени, точность же спектрального анализа задается априори размером элемента разрешения по частоте, который должен быть достаточно малым.
Обоснование способа.
Запишем обратное преобразование Фурье, связывающее анализируемый сигнал f(t) с его спектром S(ω):
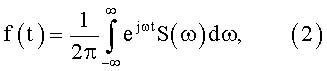
где t - время, ω - круговая частота.
Выберем интервал контролируемых частот (ωн, ωк), включающий в себя спектр анализируемого сигнала. Разобьем этот интервал на малые элементы разрешения, размер которых Ω определяется требуемой точностью спектрального анализа и перейдем от интеграла (2) к интегральной сумме
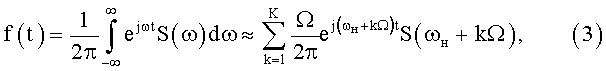
где k - номер элемента разрешения, К - число элементов разрешения в интервале контролируемых частот.
Введем обозначения:
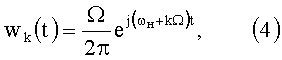
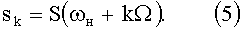
Выражение (4) определяет весовые коэффициенты при дискретных составляющих спектра сигнала (5). Для всех К элементов разрешения сформируем векторы
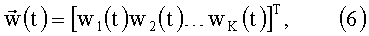
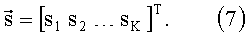
С учетом (4)-(7) перепишем интегральную сумму в правой части (3) в векторной форме:
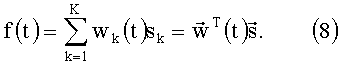
Спектральный вектор (7), входящий в (8) - это вектор дискретизированного по элементам разрешения спектра анализируемого сигнала. Определив этот вектор, мы определим спектр сигнала с точностью элемента разрешения Ω, выбранного априори.
Для определения спектрального вектора проведем измерения выборочных значений анализируемого сигнала в дискретные моменты времени. Для удобства практических измерений будем полагать эти моменты равноотстоящими на шаг дискретизации Т, который, в отличие от прототипа, выбирается исходя из возможностей измерительной техники и удобства измерений, в частности - исходя из ограниченного быстродействия АЦП. Спектр сигнала при этом не влияет на выбор шага дискретизации.
Проведенные измерения выборочных значений сигнала запишем аналогично (8) в виде системы линейных уравнений:
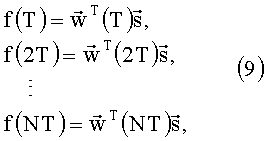
где N - число измеренных значений сигнала.
Перепишем систему уравнений (9) в векторно-матричной форме
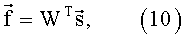
где 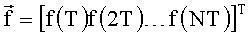 - вектор измерений,
- вектор измерений, 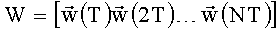 - весовая матрица.
- весовая матрица.
Компоненты весовой матрицы W определяются подстановкой в (4) моментов измерений Т, 2T, …, NT и равны
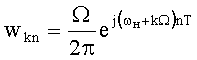
где k - номер элемента разрешения по частоте, n - номер момента измерения сигнала.
Определим оценку спектрального вектора 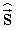 из векторно-матричного уравнения (10). Сделать это можно, например, методом псевдообращения [3]:
из векторно-матричного уравнения (10). Сделать это можно, например, методом псевдообращения [3]:
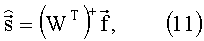
где индекс + обозначает операцию псевдообращения матрицы.
Оценка (11) является оценкой искомого спектрального вектора. Компоненты вектора 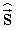 представляют собой оценки дискретизированных по элементам разрешения составляющих спектра анализируемого сигнала, что является решением поставленной задачи. Заметим, что спектральные составляющие - компоненты вектора
представляют собой оценки дискретизированных по элементам разрешения составляющих спектра анализируемого сигнала, что является решением поставленной задачи. Заметим, что спектральные составляющие - компоненты вектора 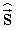 - определены с дискретностью Ω, заданной априори, по значениям временного сигнала, измеренным с шагом дискретизации Т, который задается независимо от частотного спектра сигнала, из соображений удобства проведения измерений. Это позволяет использовать более «редкие», чем в прототипе, измерения при одном и том же частотном спектре сигнала, что, в свою очередь, дает возможность применять менее быстродействующие, зато более дешевые АЦП. Кроме этого возможность выбирать отсчеты временного сигнала независимо от частоты самого сигнала позволяет проводить спетральный анализ сигналов на частотах, недоступных для оцифровки даже быстродействующими АЦП при шаге дискретизации, требуемой в прототипе.
- определены с дискретностью Ω, заданной априори, по значениям временного сигнала, измеренным с шагом дискретизации Т, который задается независимо от частотного спектра сигнала, из соображений удобства проведения измерений. Это позволяет использовать более «редкие», чем в прототипе, измерения при одном и том же частотном спектре сигнала, что, в свою очередь, дает возможность применять менее быстродействующие, зато более дешевые АЦП. Кроме этого возможность выбирать отсчеты временного сигнала независимо от частоты самого сигнала позволяет проводить спетральный анализ сигналов на частотах, недоступных для оцифровки даже быстродействующими АЦП при шаге дискретизации, требуемой в прототипе.
Преимущества предлагаемого способа по сравнению с прототипом следующие.
1. Снижение стоимости спектрального анализа, что обусловлено возможностью использования менее быстродействующих, но более дешевых АЦП по сравнению с прототипом.
2. Возможность расширения диапазона анализируемых частот в сторону высоких частот. Это является следствием того, что в заявляемом способе снимается условие 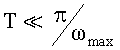 при выборе шага дискретизации временного сигнала, необходимое в прототипе.
при выборе шага дискретизации временного сигнала, необходимое в прототипе.
Источники информации
1. Голд Б., Рэйдер Ч. Цифровая обработка сигналов. Пер. с англ., под ред. A.M.Трахтмана. - М., «Советское радио», 1973, стр.187-191.
2. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. - 4-е изд., перераб. и доп. - М.: Радио и связь, 1986, стр.65.
3. Гантмахер Ф.Р. Теория матриц. 4-е изд. - М.: Наука. Гл. ред. физ.-мат. лит., 1988, с.35.
Изобретение относится к способам определения спектра электрических сигналов. Анализируемый электрический сигнал дискретизируют по времени и измеряют его дискретные выборочные значения, причем до проведения измерений интервал контролируемых частот, который включает спектр анализируемого сигнала, разбивают на элементы разрешения по частоте, размер которых определяется требуемой точностью спектрального анализа, выбирают шаг дискретизации сигнала по времени исходя из удобства проведения измерений, формируют с использованием размеров элемента разрешения и шага дискретизации весовую матрицу, измеренные выборочные значения анализируемого сигнала объединяют в вектор, составляют векторно-матричное уравнение измерений и определяют из него спектр анализируемого сигнала в виде вектора, компоненты которого представляют собой оценки дискретизированных по элементам разрешения составляющих спектра анализируемого сигнала. Технический результат заключается в расширении диапазона анализируемых частот и возможности снижения требований к быстродействию используемых АЦП.
Способ определения спектра электрического сигнала по измеренным выборочным значениям этого сигнала, заключающийся в том, что анализируемый электрический сигнал дискретизируют по времени с шагом дискретизации Т, измеряют его дискретизированные выборочные значения путем преобразования их в цифровую форму, отличающийся тем, что до проведения измерений интервал контролируемых частот (ωн, ωк), который включает спектр анализируемого сигнала, разбивают на элементы разрешения по частоте, размер которых Ω определяется требуемой точностью спектрального анализа, выбирают шаг дискретизации сигнала по времени, исходя из удобства проведения измерений, формируют весовую матрицу W с компонентами 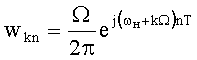 , где k - номер элемента разрешения по частоте, n - номер измеренного выборочного значения сигнала, k=1, 2, …, К, n=1, 2, …, N, К - число элементов разрешения по частоте в интервале контролируемых частот, N - число измеренных выборочных значений анализируемого сигнала, измеренные выборочные значения анализируемого сигнала f(Т)f(2Т)…f(NT) объединяют в вектор
, где k - номер элемента разрешения по частоте, n - номер измеренного выборочного значения сигнала, k=1, 2, …, К, n=1, 2, …, N, К - число элементов разрешения по частоте в интервале контролируемых частот, N - число измеренных выборочных значений анализируемого сигнала, измеренные выборочные значения анализируемого сигнала f(Т)f(2Т)…f(NT) объединяют в вектор  где индекс Т обозначает транспонирование, составляют векторно-матричное уравнение измерений
где индекс Т обозначает транспонирование, составляют векторно-матричное уравнение измерений 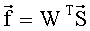 и определяют из него спектр анализируемого электрического сигнала в виде оценки спектрального вектора
и определяют из него спектр анализируемого электрического сигнала в виде оценки спектрального вектора 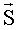 , компоненты которого представляют собой оценки дискретизированных по элементам разрешения составляющих спектра анализируемого сигнала.
, компоненты которого представляют собой оценки дискретизированных по элементам разрешения составляющих спектра анализируемого сигнала.
| Анализатор спектра | 1991 |
|
SU1799474A3 |
| Анализатор комплексного спектра | 1979 |
|
SU917119A1 |
| US 2009076737 А1, 03.19.2009 | |||
| Модуляционный способ спектрального анализа | 1984 |
|
SU1191785A1 |
Авторы
Даты
2013-02-20—Публикация
2011-10-26—Подача