Изобретение относится к физико-химическому анализу, в частности дифференциальному термическому анализу (ДТА). Для получения информации в ДТА ограничивают разными способами площадь пика фазового превращения путем восстановления (получения) базовой линии пика.
Известные способы получения базовой линии пика аналитически не формализованы, следовательно, не точны [1]
Для повышения точности используются способы, при которых считается, что базовая линия пика после окончания превращения в образце является горизонтальной прямой, представляющей собой базу измерения экспоненциального процесса, под которым подразумевается нисходящая ветвь пика ДТА [2] В этих способах полагают, что величина термической инерции образца измерена в отдельном эксперименте и, аппроксимируя нисходящую ветвь пика экспонентой, параметром которой является величина термической инерции, можно аналитически корректно получить базовую линию пика после окончания превращения в образце.
Недостатками известных способов является необходимость восстанавливать базовую линию аналитически не формализованными способами, исходя из эвристических положений, либо считать величину термической инерции образца постоянной, не зависящей от температуры нагрева.
Наиболее близким по технической сущности к предлагаемому способу является способ, основанный на аналитической формализации процесса получения базовой линии путем совокупных измерений [3] Для восстановления базовой линии нисходящей ветви пика составляют систему условных уравнений, в левой части которых записывают сумму двух процессов с искомыми параметрами: полиномиального процесса, описывающего изменение базовой линии пика, и экспоненциального процесса, характеризующего процесс возврата образца в квазистационарное состояние нагрева после фазового превращения, а в правой части величины измерения разности температур между держателем образца и держателем эталона. В результате решения этой нелинейной системы уравнений определяются параметры полинома, позволяющие получить базовую линию пика после окончания превращения в образце.
Недостатком способа является необходимость постулировать постоянство величины термической инерции образца, характеризующей экспоненциальный процесс возврата образца в квазистационарное состояние после фазового превращения (нисходящая ветвь пика), а также обеспечить практическое решение нелинейной системы условных уравнений, которая при составлении часто становится некорректной из-за погрешностей измерения разности температур между держателем образца и эталоном.
Целью изобретения является повышение точности в получении базовой линии пика после окончания превращения в исследуемом образце в ДТА за счет учета зависимости величины термической инерции образца от времени нагрева (температуры).
Способ осуществляется следующим образом.
В основной стадии нагрева в держатель образца (индекс S) помещают исследуемый термоактивный образец и производят нагрев термоаналитической установки, в процессе которого осуществляют дискретные измерения в момент времени ti текущей разности температур между держателем образца и держателем эталона (индекс R) Δ TSR(ti tc) в интервале времени tc ≅ ti≅ tn, где tс момент времени окончания фазового превращения в исследуемом образце и начала измерения; tn момент времени окончания процесса измерения. В дополнительной стадии нагрева в держатель образца помещают индифферентный в диапазоне исследуемого фазового превращения образец, одновременно измеряют текущие скорость 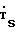 (ti tc) роста температуры при нагреве держателя образца и разность температуры между нагревательным элементом (индекс Р) и держателем образца Δ TSP(ti tc), далее рассчитывают термическую инерцию θ держателя образца по формуле, как величину, зависящую от времени нагрева (температуры)
(ti tc) роста температуры при нагреве держателя образца и разность температуры между нагревательным элементом (индекс Р) и держателем образца Δ TSP(ti tc), далее рассчитывают термическую инерцию θ держателя образца по формуле, как величину, зависящую от времени нагрева (температуры)
θ 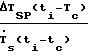 θ(ti-tc), (1) а параметры полинома (ao, a1.am), аппроксимирующего базовую линию пика и предэкспоненциальный множитель А (обусловлен начальной разностью температур ΔTSR(ti to) ao + A при ti tc и является вспомогательным параметром при составлении уравнений), определяют из системы n линейных уравнений
θ(ti-tc), (1) а параметры полинома (ao, a1.am), аппроксимирующего базовую линию пика и предэкспоненциальный множитель А (обусловлен начальной разностью температур ΔTSR(ti to) ao + A при ti tc и является вспомогательным параметром при составлении уравнений), определяют из системы n линейных уравнений
ao+a1(ti-tc)+.+ai(ti-tc)i+.+am(ti-tc)m+A exp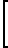 -
- 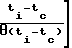 ΔTSR(ti-tc) (2) где i 0, 1, 2.mn; n >> m.
ΔTSR(ti-tc) (2) где i 0, 1, 2.mn; n >> m.
Рассмотрим определение базовой линии пика в соответствии с предлагаемым способом в предположении что базовая линия пика после окончания фазового превращения в образце представляет собой полином первой степени ao + a1(ti tc).
Система уравнений для определения базовой линии в этом случае, согласно (2) принимает вид
ao + A ΔTSR(ti tc)
ao+a1(t1-tc)+A exp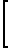 -
- 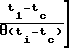 =ΔTSR(t1-tc)
=ΔTSR(t1-tc)
ao+a1(ti-tc)+A exp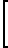 -
- 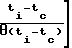 =ΔTSR(ti-tc)
=ΔTSR(ti-tc)
ao+a1(tn-tc)+A exp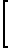 -
- 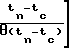 =ΔTSR(tn-tc) где i 0, 1, 2.n; n>>2,
=ΔTSR(tn-tc) где i 0, 1, 2.n; n>>2,
θ(ti-tc) 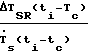 вычисляется по данным дополнительной стадии нагрева.
вычисляется по данным дополнительной стадии нагрева.
Решение линейной системы уравнений с неизвестными ao, a1 и А эффективно осуществляется методом наименьших квадратов, устойчивым к погрешности измерений ΔTSR(ti tc)
Введем обозначения
ti=x1(i); exp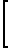 -
- 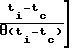 =x2(i); ΔT(ti-tc)=y(i);
=x2(i); ΔT(ti-tc)=y(i);
ao C1; a1 C2; A C3
Тогда можно записать
y(i) C1 + C2x1(i) + C3x2(i) для вычисления С1, С2 и С3 выпишем функционал невязок
F 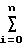 [C1+C2x1(i)+C3x2(i)-y(i)]2, минимизируя его по С1, С2 и С3
[C1+C2x1(i)+C3x2(i)-y(i)]2, минимизируя его по С1, С2 и С3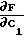 2
2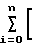 C1+C2x1(i)+C3x2(i)-y(i)
C1+C2x1(i)+C3x2(i)-y(i) =0;
=0;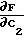 2
2 C1+C2x1(i)+C3x2(i)-y(i)
C1+C2x1(i)+C3x2(i)-y(i)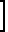 x1(i)=0;
x1(i)=0;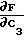 2
2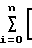 C1+C2x1(i)+C3x2(i)-y(i)
C1+C2x1(i)+C3x2(i)-y(i)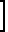 x2(i)=0, получим систему уравнений
x2(i)=0, получим систему уравнений
C1(n+1)+C2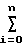 x1(i)+C
x1(i)+C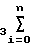 x2(i)
x2(i)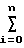 y(i);
y(i);
C1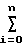 x1(i)+C2
x1(i)+C2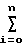 x
x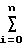 x1(i)x2(i)
x1(i)x2(i) 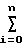 y(i)x1(i);
y(i)x1(i);
C1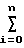 x2(i)+C2
x2(i)+C2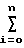 x1(i)x2(i)+C3
x1(i)x2(i)+C3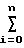 x
x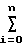 y(i)x2(i).
y(i)x2(i).
Для решения системы уравнений удобно применить правило Крамера, предварительно рассчитав определители Δ Δ1 Δ2 Δ3, а затем C1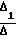 ; C2
; C2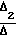 ; C3
; C3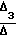 .
.
Использование: в технике измерения параметров физико-химических превращений, осуществляемых методом дифференциального термического анализа. Сущность изобретения: проводят дополнительный нагрев термоаналитической установки, при котором измеряют скорость нагрева держателя образца при нахождении в держателе индифферентного в диапазоне температур фазового превращения образца, измеряют разность температур между держателем образца и нагревательным элементом термоаналитической установки, величину термической инерции образца рассчитывают с учетом временной (температурной) нестационарности по известной формуле, параметры полинома аппроксимирующего базовую линию пика рассчитывают из системы уравнений.
СПОСОБ ОПРЕДЕЛЕНИЯ БАЗОВОЙ ЛИНИИ ПИКА ПОСЛЕ ОКОНЧАНИЯ ФАЗОВОГО ПРЕВРАЩЕНИЯ В ОБРАЗЦЕ В ДИФФЕРЕНЦИАЛЬНОМ ТЕРМИЧЕСКОМ АНАЛИЗЕ, заключающийся в нагреве держателя образца с исследуемым образцом и держателя эталона с помощью нагревательного элемента, измерения текущей разности температур между держателем образца и держателем эталона, расчете параметров полинома, аппроксимирующего базовую линию пика, отличающийся тем, что осуществляют дополнительную стадию нагрева, при которой нагревают в держателе образца индифферентный в диапазоне исследуемого фазового превращения образец, измеряют текущие скорость нагрева держателя образца 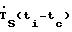 и разность температур между держателем образца и нагревательным элементом ΔTSP(ti-tc), по которым рассчитывают величину термической инерции θ(ti-tc) держателя образца в зависимости от времени нагрева по формуле
и разность температур между держателем образца и нагревательным элементом ΔTSP(ti-tc), по которым рассчитывают величину термической инерции θ(ti-tc) держателя образца в зависимости от времени нагрева по формуле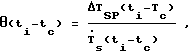
а параметры полинома находят из системы линейных условных уравнений вида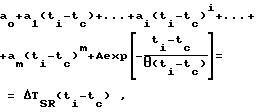
где i 0,1,2. m n; n>>m целые числа;
ti дискретный момент времени измерений, причем tc≅ti≅tn;
tc момент времени окончания фазового превращения в исследуемом образце и начала измерений;
tn момент времени окончания измерений;
a0, a1. ai.am искомые параметры полинома a0+a1(t1-tc) + + ai(ti-tc)i +.+ am(ti-tc)m, аппроксимирующего базовую линию пика;
ΔTSR(ti-tc) разность температур между держателем образца и эталоном в дискретные моменты времени измерений;
A предэкспоненциальный множитель, обусловленный исходной разностью температур, определяемый при ti=tc.
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Егунов В.П | |||
| Традиентная теория термического анализа | |||
| Теория, методика, аппаратура, дисс | |||
| на соиск | |||
| учен | |||
| степени д-а хим | |||
| наук | |||
| М | |||
| Пневматический водоподъемный аппарат-двигатель | 1917 |
|
SU1986A1 |
Авторы
Даты
1995-09-27—Публикация
1991-11-25—Подача