Изобретение относится к автоматике, телемеханике и вычислительной технике, в частности к обработке данных дистанционных измерений, получаемых с помощью метеорологических спутников Земли.
Известно устройство [1] позволяющее эффективно сжимать двумерные массивы информации лишь в случае существования элементов массива, мало отличающихся по строке и/или столбцу. Наиболее близким к изобретению является устройство для сжатия двумерного массива информации [2] обеспечивающее получение более высокого коэффициента сжатия, чем упомянутое выше устройство. Эффект большего сжатия в этом устройстве достигнут благодаря использованию регрессионной модели второго порядка в качестве средства приближенного описания данных, содержащихся в двумерном массиве. Оно содержит блок сокращения избыточности по строкам и столбцам, формирователи (постоянные запоминающие устройства) коэффициентов регрессионного сжатия по строкам и столбцам и синхронизатор. Блок сокращения избыточности по строкам и столбцам содержит шесть одинаковых блоков формирования элементов выходного массива, обеспечивающих умножение элементов входного массива на коэффициенты регрессионного сжатия по строкам и столбцам и накопление шести сумм произведений, являющихся элементами выходного массива информации. При этом информация, содержащаяся во входном массиве размерностью n1 x n2 элементов, передается с помощью шести чисел. Максимальная размерность n1 x n2 входного массива, который может быть сжат с помощью этого устройства, определяется степенью сложности и монотонности двумерной зависимости, соответствующей этому числовому массиву. Формирователи элементов выходного массива, входящие в состав блока сокращения избыточности, содержат каждый два умножителя и два накапливающих сумматора.
Недостатком этого устройства является то, что сжатие информации (с возможностью точного воспроизведения исходных данных при восстановлении) обеспечивается только для числовых массивов, соответствующих монотонным двумерным зависимостям. Это обусловлено тем, что в известном устройстве реализована регрессионная модель невысокого (второго) порядка. Кроме того, это устройство не обеспечивает сжатие информации, если элементы числового массива содержат случайную составляющую.
Целью изобретения является сокращение избыточности передаваемой информации, содержащей случайную составляющую и отображающей сложные немонотонные двумерные зависимости.
Главным существенным отличием изобретения является введение в состав системы блока формирования сжатых данных, блока восстановления и блока формирования корректирующих данных. Вторым существенным отличием является введение в состав блока сокращения избыточности М + 1 формирователей группы правых частей нормальной системы, М + 1-разрядного регистра и умножителя.
Данные отличия являются существенными, так как эти признаки в прототипе и аналогах отсутствуют. Введение первого отличия позволяет до передачи данных произвести восстановление числового массива по сжатой информации, вычислить корректирующий массив разностей элементов исходного и восстановленного массива и передать не только массив сжатых данных, но и этот корректирующий массив разностей. Этим обеспечивается точное восстановление исходного числового массива по сжатой информации после передачи во всех случаях, в том числе и при наличии случайной составляющей в исходном числовом массиве.
Введение второго отличия позволяет обеспечить сжатие двумерных числовых массивов информации, отображающих сложные немонотонные зависимости, так как в предлагаемой системе в блоке сокращения избыточности реализована регрессионная модель сжатия М-го порядка (М ≥ 2).
Рассмотрим сжатие двумерного массива информации TijТ (X1i, X2j), содержащего N (2n1 + 1)(2n2 + 1) чисел, где 2n1 + 1 количество чисел в строке массива; 2n2 + 1 количество чисел в столбце массива; X1i i, -n1 ≅ i ≅ n1; X2j j, -n2 ≅ j ≅ n2.
Рассмотрим полиномиальную регрессионную модель М-го порядка: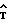 (X1, X2)
(X1, X2)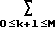 bklX
bklX
Для определения коэффициентов регрессии bkl воспользуемся методом наименьших квадратов. Тогда система уравнений для вычисления коэффициентов имеет вид
Cb d, (1) где С ХтХ; d ХтТ;
b искомый столбец коэффициентов bkl;
d столбец правых частей dkl нормальной системы уравнений.
Матрица С симметрична и ее порядок равен числу базисных функций модели, т.е.
L  (M+1)(M+2)
(M+1)(M+2)
Для вычисления элементов этой матрицы требуется примерно  LN LN операций умножения. Однако для полиномиальной модели в случае равномерной сетки можно построить алгоритм, в котором число операций не зависит от числа узлов сетки, а определяется лишь порядком модели М.
LN LN операций умножения. Однако для полиномиальной модели в случае равномерной сетки можно построить алгоритм, в котором число операций не зависит от числа узлов сетки, а определяется лишь порядком модели М.
Матрица С имеет не более L различных элементов вида
Аkl= Ak(1)Al(2); 0=≅k+l≅M,(2) где A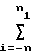 X
X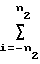 X
X
Коэффициенты вида Ak и Al определяются из рекуррентных формул:
Ak= 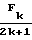 (3) где Fo 2n + 1; ε n (n + 1);
(3) где Fo 2n + 1; ε n (n + 1);
Fk= εkFo-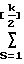
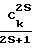 Fk-S . (4) Имеем Ao 2n + 1; ε n (n + 1); (5)
Fk-S . (4) Имеем Ao 2n + 1; ε n (n + 1); (5)
3A1 ε Ao;
5A2 ε 2Ao A1;
7A3 ε 3Ao 5A2;
9A4 ε 4Ao 14A3 A2;
11A5 ε 5Ao 30A4 7A3;
13A6 ε 6Ao 55A5 27A4 A3 и т.д.
Полагая n n1 и ε ε1, находим коэффициенты Ak(1), при n n2 и ε ε2 определяем коэффициенты Al(7), после чего путем перемножения найденных коэффициентов определяем остальные  M (M-1) коэффициентов Akl.
M (M-1) коэффициентов Akl.
Показано, что при подходящей нумерации базисных функций модели матрица коэффициентов нормальной системы является клеточно-диагональной:
C 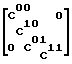 и расщепляется на четыре независимых системы с матрицами коэффициентов С00, С10, С01 и С11. В каждой из этих систем нумерация коэффициентов регрессии bkl и правых частей dkl совпадает с нумерацией диагональных элементов Akl соответствующей матрицы коэффициентов:
и расщепляется на четыре независимых системы с матрицами коэффициентов С00, С10, С01 и С11. В каждой из этих систем нумерация коэффициентов регрессии bkl и правых частей dkl совпадает с нумерацией диагональных элементов Akl соответствующей матрицы коэффициентов:
C diag (C00, C10, C01, C11), (6) что приводит к расщеплению нормальной системы (6) на четыре независимых подсистемы:
C00B00 D00; C01B01 D01;
C10B10 D10; C11B11 D11. (7)
Порядки клеток отдельных матриц связаны с числом базисных функций L и порядком модели М соотношениями
L 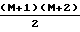 P00+P10+P01+P11 Если М четное, то
P00+P10+P01+P11 Если М четное, то
P00=  (M+2)(M+4);
(M+2)(M+4);
P10= P01=P11=  M(M+2). Если М нечетное, то
M(M+2). Если М нечетное, то
P11=  (M2-1)
(M2-1)
P00= P10= P01=  (M+1)(M+3) Для М ≅ 6 порядки клеток приведены в таблице.
(M+1)(M+3) Для М ≅ 6 порядки клеток приведены в таблице.
Для определения элементов матрицы С моделей меньших порядков применяется следующий алгоритм. Пусть заданы одномерные массивы q (0 10 210 3210 43210 543210 6543210) h (0 01 012 0123 01234 0123456) Тогда
Сrs00 Akl; 1 ≅ r1s ≅ P00;
Crs10 Ak+1,l; 1 ≅ r1s ≅ P10;
Crs01 Ak,l+1; 1 ≅ r1s ≅ P01;
Crs11 Ak+1,l+1; 1 ≅ r1s ≅ P11, где k gr + gs; l hr + hs.
В качестве примера выпишем верхнюю треугольную часть клеток матрицы С для модели шестого порядка:
A00A10A01A20A11A02A30A21A12A03
A20A11A30A21A12A40A31A22A13
A02A21A12A03A31A22A13A04 C00 A40A31A22A50A41A32A23 (8)
A22A13A41A32A23A14
A04A32A23A14A05
A60A51A42A33
A42A33A24
A24A15
A06
A10A20A11A30A21A12
A30A21A40A31A22 C10 A12A31A22A13 (9)
A50A41A32
A32A23
A14
A01A02A11A03A12A21
A03A12A04A13A22 C01 A21A13A22A31 (10)
A05A14A23
A23A32
A41
A11A21A12A31A22A13
A31A22A41A32A23 C11 A13A32A23A14 (11)
A51A42A33
A33A24
A15
При использовании МНК наибольшее количество операций требуется для вычисления правых частей dkl:
dkl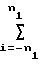
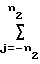 X
X
Двойная сумма может быть преобразована к повторной сумме
S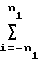 X
X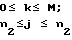 ; (13)
; (13)
Sjkl SjkoX2jl; O ≅ k + l≅ M;
n ≅ j ≅ n2; (14)
dkl= 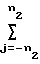 S
S
Это позволяет сократить число операций умножения при вычислении правых частей с 2NL до NM + (2n2 + 1)L и облегчает задачу обработки данных в темпе их поступления по строкам массива Т.
Решив четыре независимых системы уравнений, находим коэффициенты регрессии
B00 (C00)-1 D00;
B01 (C01)-1 D01;
B10 (C10)-1 D10; (16)
B11 (C11)-1 D11;
B00= 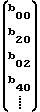 ; B10
; B10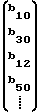 ; B01=
; B01= B11=
B11=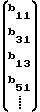 (17)
(17)
Если потребителей информации несколько и требования к точности восстановления данных по сжатой информации различны, возможно представление сжатых данных как комбинации коэффициентов регрессионной модели и массива корректирующих данных, так и только коэффициентов регрессионной модели. В последнем случае коэффициент сжатия максимален, а точность восстановления минимальна.
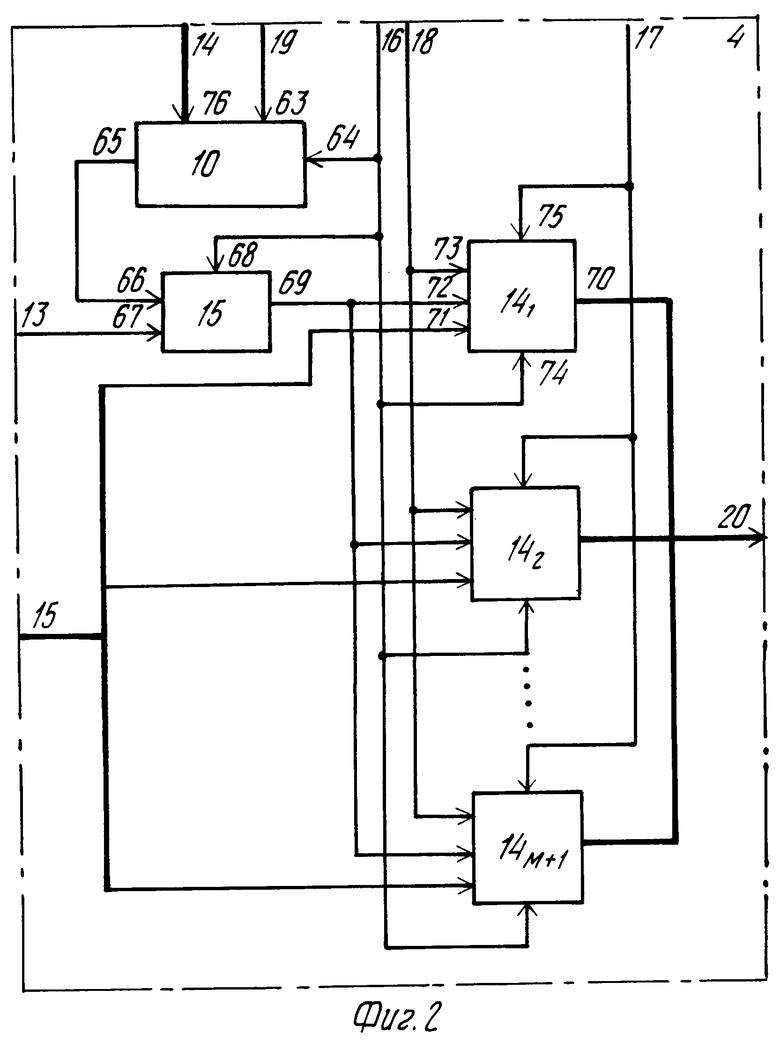
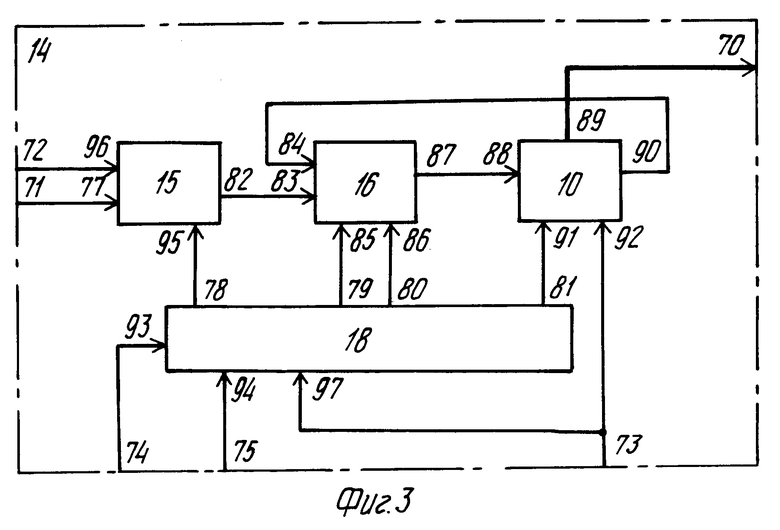
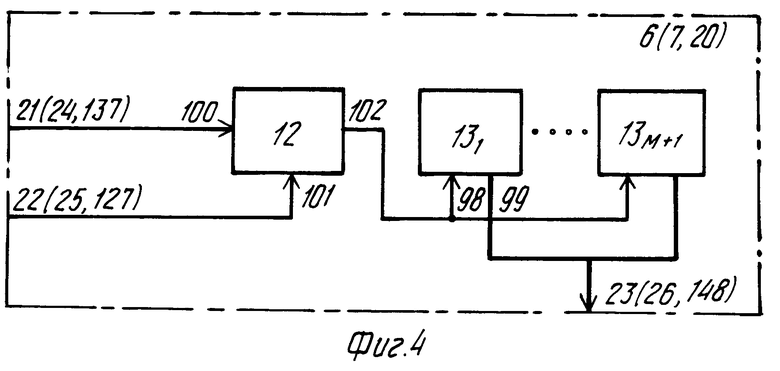
На фиг. 1 изображена блок-схема системы для сжатия двумерного массива информации; на фиг. 2 схема блока сокращения избыточности; на фиг. 3 схема формирователя группы коэффициентов правых частей нормальной системы; на фиг. 4 схема постоянного запоминающего устройства (ПЗУ) коэффициентов регрессионного сжатия по строкам, столбцам и ПЗУ коэффициентов обратной матрицы; на фиг. 5 схема блока формирования сжатых данных; на фиг. 6 схема вычислителя группы коэффициентов регрессионной модели; на фиг. 7 схема накопителя суммы попарных произведений; на фиг. 8 схема блока восстановления; на фиг. 9 схема блока формирования корректирующих данных; на фиг. 10 схема синхронизатора; на фиг. 11-13 временная диаграмма работы системы для сжатия двумерного массива информации; на фиг. 14 схема делителя частоты по модулю Р; на фиг. 15-17 и 18 схемы регистров, используемых в синхронизаторе.
Система для сжатия двумерного массива информации (фиг. 1) включает источник 1 информации, дискретизатор 2, аналого-цифровой преобразователь (АЦП) 3, блок 4 сокращения избыточности, синхронизатор 5, ПЗУ 6 коэффициентов регрессионного сжатия по строкам, ПЗУ 7 коэффициентов регрессионного сжатия по столбцам, блок 8 формирования сжатых данных, блок 9 восстановления, сдвиговый регистра 10 и блок 11 формирования корректирующих данных.
Блок 4 сокращения избыточности (фиг. 2) содержит М + 1-разрядный регистр 10, М + 1 формирователей 14 группы коэффициентов правых частей нормальной системы и умножитель 15.
Формирователь 14 группы коэффициентов правых частей нормальной системы (фиг. 3) содержит умножитель 15, сумматор 16, М + 1-разрядный регистр 10 и четырехразрядный регистр 18.
ПЗУ коэффициентов регрессионного сжатия по строкам (фиг. 4) содержит счетчик 12 и М + 1 блоков 13 памяти.
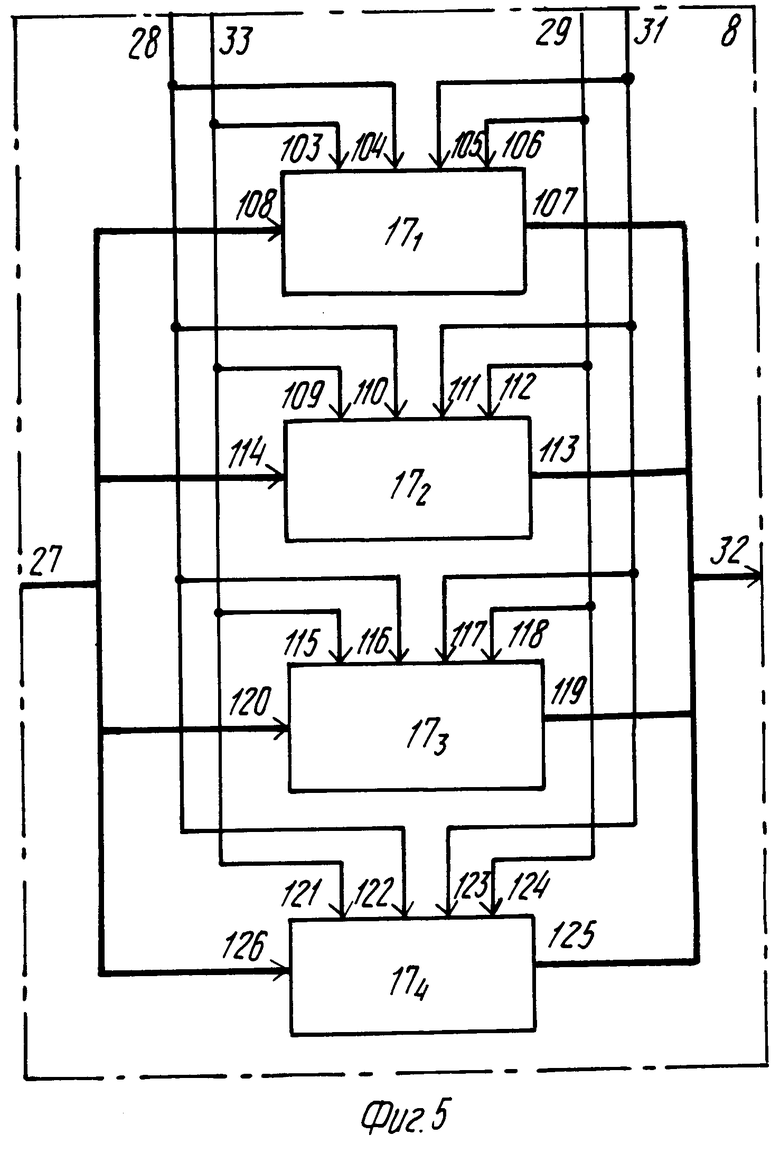
Блок 8 формирования сжатых данных (фиг. 5) содержит четыре вычислителя 17 группы коэффициентов регрессионной модели.
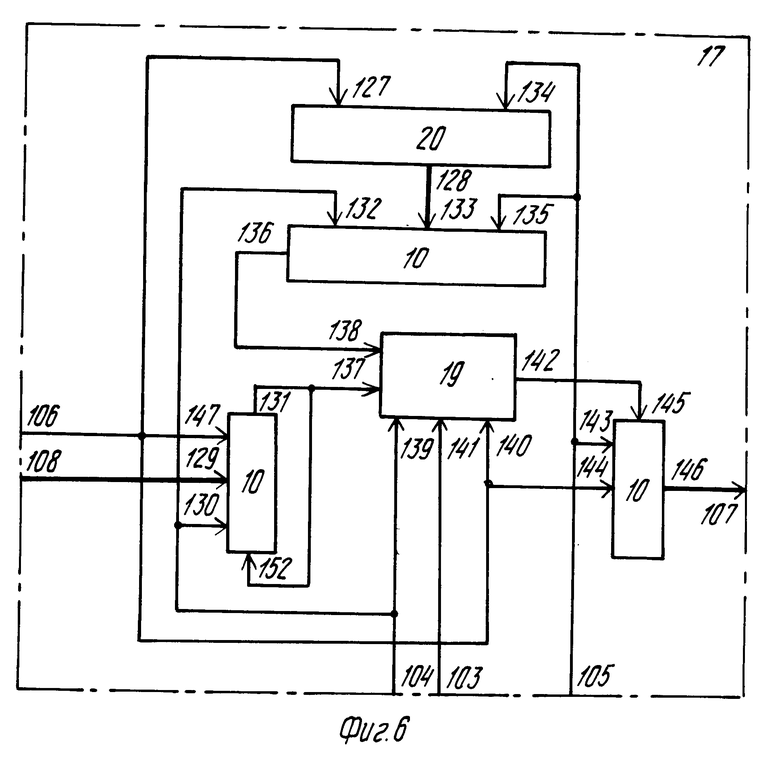
Вычислитель группы коэффициентов регрессионной модели (фиг. 6) содержит три Р-разрядных регистра 10, накопитель 19 суммы попарных произведений и ПЗУ 20 коэффициентов обратной матрицы.
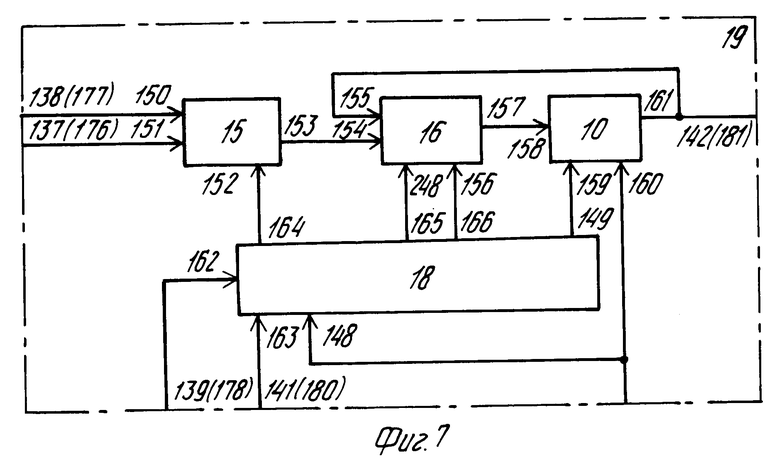
Накопитель 19 суммы попарных произведений (фиг. 7) содержит умножитель 15, сумматор 16, четырехразрядный регистр 18 и одноразрядный регистр 10.
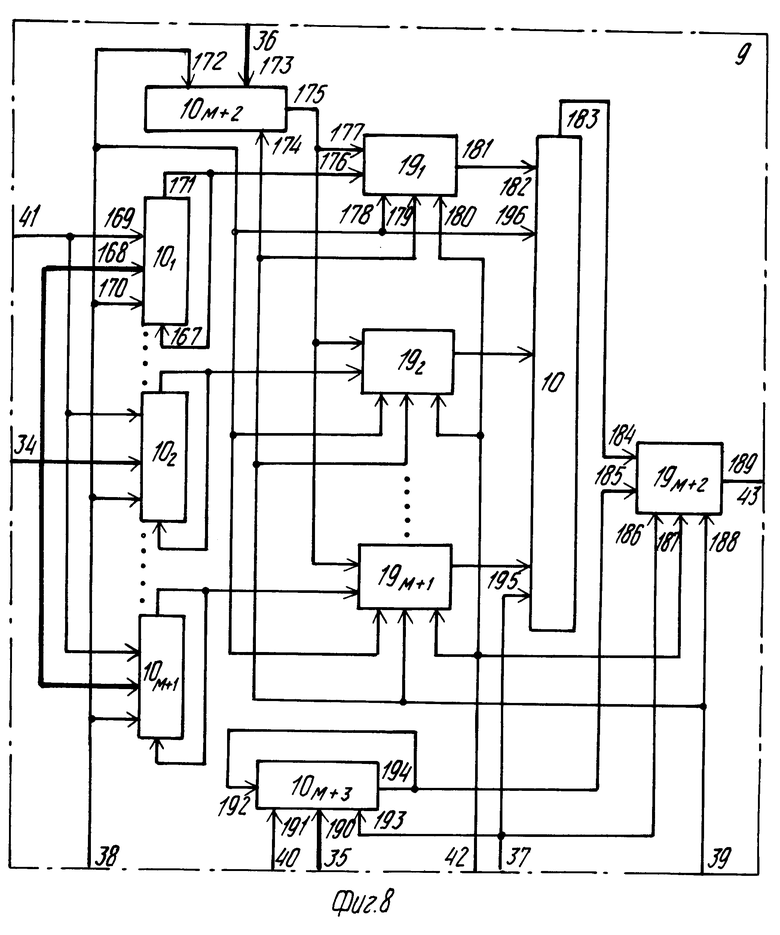
Блок 9 восстановления (фиг. 8) содержит М + 4 М + 1-разрядных сдвиговых регистров 10 и М + 2 накопителей 19 суммы попарных произведений.
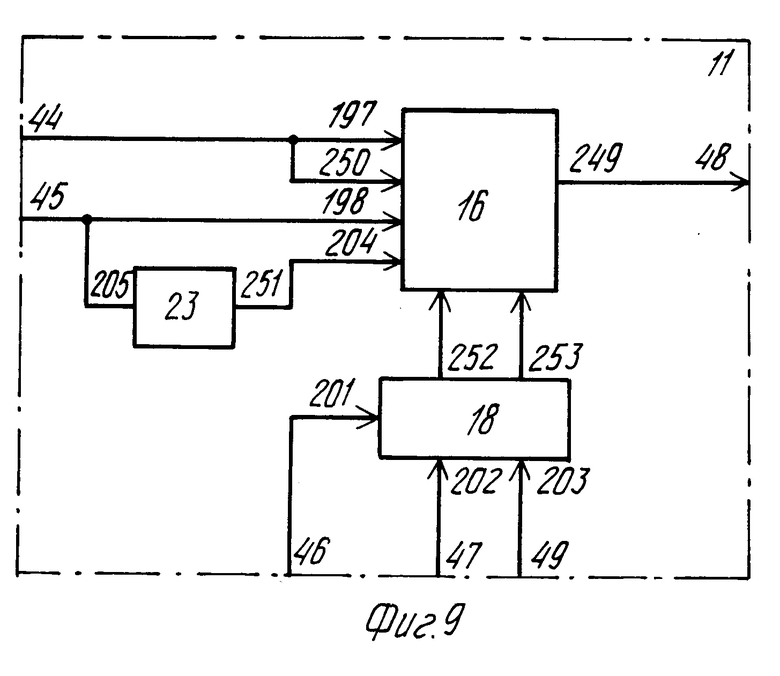
Блок 11 формирования корректирующих данных (фиг. 9) содержит сумматор 16, инвертор 23 и двухразрядный регистр 18.
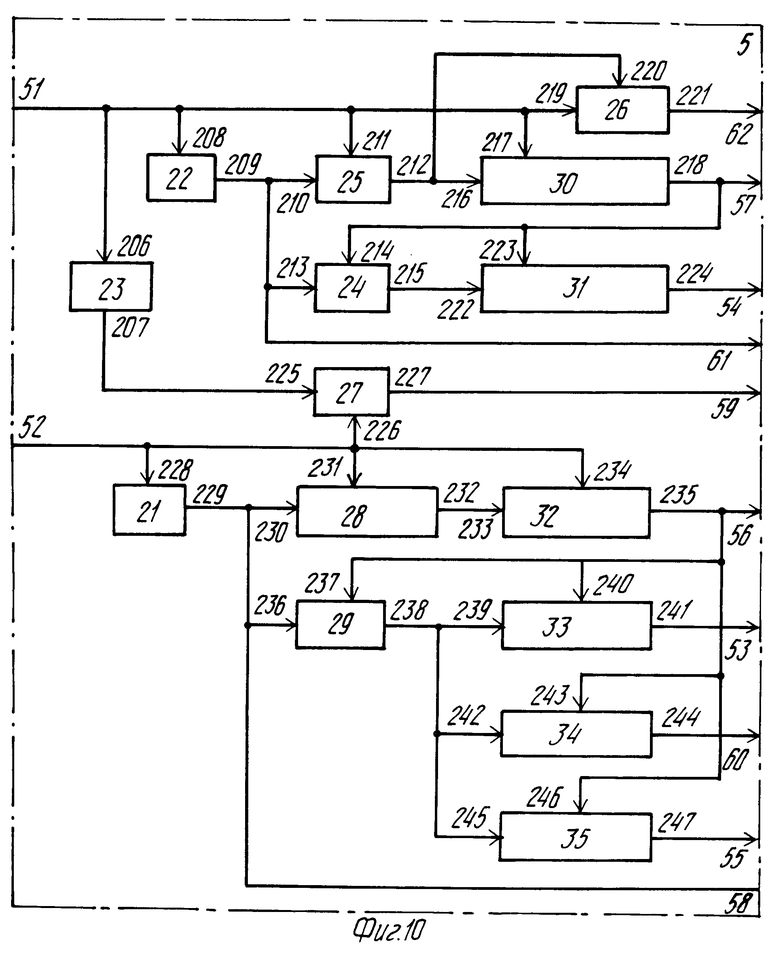
Синхронизатор 5 (фиг. 10) содержит генератор 21 тактовых импульсов ТИ1, генератор 22 тактовых импульсов ТИ2, инвертор 23, делители 24-29 частоты по модулю 4, 4Р, Р + 1, n2 + 1, (2М + 3) ˙ n1, 2М + 3 соответственно, регистры 30, 31, 32, 33, 34, 35 с числом разрядов Р, Р, n1, М + 1, М + 2, 2М + 3 соответственно.
Все входы и выходы элементов и узлов, используемых в системе для сжатия двумерного массива информации, изображенные на фигурах 1-10 и 12-14, имеют сквозную нумерацию с 1 по 247.
Система для сжатия двумерного массива информации работает следующим образом.
Аналоговые сигналы, представляющие функцию двух аргументов и получаемые путем сканирования в фиксированной прямоугольной области пространства аргументов, с выхода источника 1 информации поступают на вход дискретизатора 2, который производит выборку и запоминание мгновенных значений сигнала через фиксированные интервалы времени, обеспечивая тем самым представление двумерной информации в виде набора значений аналогового сигнала. АЦП 3 преобразует аналоговые сигналы, поступающие с выхода дискретизатора 2, в двоичный код. Таким образом, набор кодов на выходе АЦП представляет собой двумерный числовой массив инфоpмации, полученный путем разложения функции двух аргументов на фиксированное число элементов по n2 строкам и n1 столбцам. Элементы этого массива с выхода АЦП последовательно строка за строкой поступают на вход последовательных данных регистра 10 и на вход блока 4 сокращения избыточности. Основой для синхронизации работы всего устройства являются кадровый синхроимпульс (КСИ) и строчный синхроимпульс (ССИ), формируемые источником 1 информации и поступающие потребителям с первого и второго выходов источника соответственно. Импульс синхронизации момента формирования отдельного отсчета Tij в пределах кадра формируется синхронизатором 5 и поступает на пятый вход дискретизатора 2 и восьмой вход АЦП.
Блок 4 сокращения избыточности (фиг. 2) формирует значения правых частей нормальной системы dkl. На четырнадцатый вход блока 4 одновременно подаются коды, соответствующие значениям степеней первого фактора 1, X1i, X1i2, X1iM. С такой же периодичностью на тринадцатый вход поступает значение Tij, где i номер столбца; j номер строки. Умножитель 15 (фиг. 2) формирует значения Tij, X1iTij, X1iMTij, поступающие с частотой следования импульсов С3 на входы 72 формирователей 14 группы коэффициентов правых частей нормальной системы. На третий групповой вход блока 4 (фиг. 2, вход 15) поступают значения второго фактора 1, X2j, X2j2, X2jM причем первое из этих значений поступает на вход 71 первого (верхнего на фиг. 2) формирователя 14, а последнее из значений на аналоговый вход (М + 1)-го формирователя.
Таким образом, на выходе умножителя 15 в схеме первого формирователя (фиг. 2) получается последовательность произведений 1.Tij, X1iTij, X1iMTij, поступающая с частотой управляющих импульсов серии СЗ (фиг. 12) на сумматор 16 (фиг. 3).
В (М + 1)-м формирователе 14 (фиг. 2) на выходе умножителя 15, входящем в его состав (фиг. 3), образуется последовательность произведений 1˙Tij, X1i˙Tij˙X2j, X1iMTijX2jM. После этого меняется значение i, т.е. на четырнадцатый вход блока 4 по- даются значения степеней первого фактора, соответствующих следующей в строке точке отсчета функции Tij. При этом информация на пятнадцатом входе меняется только тогда, когда все значения Tij в строке введены в блок 4. Это обеспечивается тем, что на вход 22 (25) ПЗУ 6 (7) подаются сигналы сброса счетчиков на "0" в моменты формирования строчного синхроимпульса ССИ (или сигнал конца кадрового синхроимпульса ККСИ), а на счетный вход 21 (24) счетчика 12 поступают импульсы серии С1, следующие синхронно с поступлением значений Tij на ПЗУ 6, или ССИ, поступающие с частотой следования строк на ПЗУ 7.
Формирователь 14 (фиг. 3) работает следующим образом.
В регистре 10 формирователя хранятся значения Sjkl, причем О ≅ k + l ≅ 2M, которые суммируются на каждом цикле серии импульсов С3, поступающей на вход 73, с ранее накопленной суммой 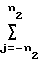 S
S
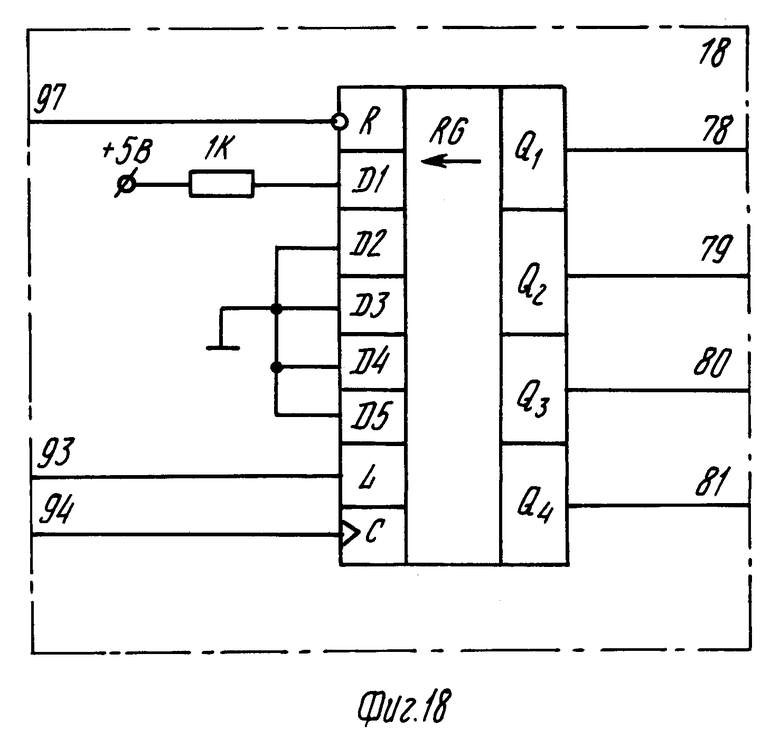
Для синхронизации работы формирователей на вход 93 управления записью регистров 18 (фиг. 14) подаются импульсы серии С3, каждый импульс серии инициализирует одну операцию суммирования. При этом на вход 75 формирователей подаются импульсы сдвига по регистру 18 записанной в него единицы. На выходах разрядов регистра 18 (на фиг. 3) формируются сигналы синхронизации работы умножителя 15 (выход 78), синхронизации записи в регистры сумматора 16 (выход 79), сигнал записи результата суммирования в выходной регистр сумматора 16 (выход 80), сигнал сдвига информации в регистре 10 (выход 81). Начальный сброс регистра 10 и регистра 18 осуществляется подачей сигнала на вход 73 формирователей 14 в начале каждого кадра.
Блок 8 формирования сжатых данных (фиг. 5) вычисляет коэффициенты регрессионной модели bkl, используя значения элементов правых частей dkl, формируемых в блоке 4 сокращения избыточности, и коэффициентов обратной матрицы С-1, которые хранятся в ПЗУ 20 (фиг. 6) коэффициентов обратной матрицы. При этом реализуются выражения (16), причем все четыре подвектора искомых коэффициентов регрессионной модели вычисляются одновременно в соответствии с формулами (17). Для однотипности вычислений матрицы (С00)-1, (С10)-1, (С01)-1, (С11)-1 берутся одинаковых размеров, определяемых наибольшим размером РmaxPij, i, j 0, 1, причем на места недостающих элементов в ПЗУ записаны нули. Подвекторы В00, В10, В01, В11 имеют размеры Р00 Р1, Р10 Р2, Р01 Р3, Р11 Р4.
Блок 8 имеет один групповой вход 27, по которому поступают значения dkl, четыре входа 28, 29, 31, 33 синхронизации и один групповой выход 32, причем на групповой вход поступает L значений dkl, а на групповом выходе получается L значений bkl (четыре подвектора Вij).
Рассмотрим работу первого (верхнего на фиг. 5) вычислителя 17 группы коэффициентов регрессионной модели (фиг. 6). Регистры 10 вычислителя Р-разрядные. С группового входа 108 вычислителя на ортогональные входы 129 регистра 10 поступает одновременно Р1 значений dkl в старшие разряды. Одновременно из ПЗУ 20 коэффициентов обратной матрицы параллельно передается вся строка обратной подматрицы (С00)-1 из Р чисел в регистр 10 (ортогональный вход 133). Значения подвектора D00 и одной из строк матрицы (С00)-1 последовательно выводятся на входы 138 и 137 накопителя 19 суммы попарных произведений. При этом импульсы сдвига подаются на входы 130 и 132 синхронизации сдвига, а синхронизация записи чисел в регистре 10 из ПЗУ осуществляется подачей управляющего сигнала на вход 135. Подвектор D00 при сдвиге регистра 10 одновременно записывается по входу 152 последовательных данных снова в регистр и находится в нем, пока не умножится последовательно на все строки подматрицы (С00)-1. В накопителе суммы попарных произведений (фиг. 7) умножитель 15 производит умножение элемента строки подматрицы (С00)-1 на элемент подвектора D00, произведение поступает на вход 154 сумматора 16, на второй вход 155 которого поступает ранее накопленная сумма, и результат записывается в регистр 10 по входу 158. Под действием импульса сдвига регистра, подаваемого на вход 159, накопленная ранее сумма попарных произведений снова поступает на вход 155 сумматора 16. Таким образом, через Р циклов суммирования на выходе 142 формируется один элемент bkl подвектора В00 коэффициентов регрессионной модели. Это значение записывается по входу 145 в регистр 10 (фиг. 6). После Р повторений этой процедуры в регистре 10 на Р1 ортогональных выходах 146 получается значение всего подвектора В00. Аналогично формированию подвектора В00 формируются подвекторы В01, В10 и В11 на выходах 113, 119 и 125 (фиг. 5). Общее число коэффициентов, формируемых на выходе 32 блока 8, равно L Р1 + Р2 + Р3 + Р4.
В накопителе 19 (фиг. 7) четырехразрядный регистр 18 используется в качестве местного синхронизатора, аналогичного регистру 18 на фиг. 3. При этом в первый разряд сдвигового регистра записывается "1" подачей управляющего сигнала на вход 162, а импульсы сдвига подаются на вход 163 регистра 18 (фиг. 7).
Блок 9 восстановления (фиг. 8) работает следующим образом. На первый групповой вход 34 блока параллельно подаются L коэффициентов регрессионной модели bkl (0 ≅ k + l ≅ M). При этом по регистрам 10 они распределены следующим образом. На ортогональные входы 168 верхнего регистра 10 подаются М + 1 коэффициентов bkl (lo0, 0 ≅ k ≅ M), на ортогональные входы второго регистра 10 подаются М коэффициентов bkl, причем в самый младший разряд ничего не подается, т. е. туда записывается "0" (l 1, 0 ≅ k ≅ M 1). В последний (М + 1)-й регистр по групповому входу 34 поступает лишь один коэффициент bkl (l M, k 0) в самый старший разряд, начиная с которого осуществляется вывод из регистра.
По синхроимпульсу серии С3 (вход 38 фиг. 8) осуществляется запись значений bkl в (М + 1)-й регистр с группового входа и запись значений степеней первого фактора 1, X1i, X1i2, X1iM по второму групповому входу 36 в (М + 2)-й регистр 10, а по строчному импульсу ССИ, поступающему по входу 40, с третьего группового входа 35 в (М + 3)-й регистр записываются значения степеней второго фактора 1, X2j, X2j2, X2jM. На входы 176, 177 (фиг. 8) одновременно поступают значения b00, b10, bM0 и 1, X1i, X1i2, X1iM, а на выходе 181 накопителя 19 суммы попарных произведений получается сумма (М + 1)-го слагаемого регрессионной модели, записываемого в младший разряд (М + 4)-го регистра 10 по ортогональному входу 182. Другими словами, при М 3, например, формируется сумма b00˙1 + b10˙X1i + b20X1i2 + b30˙X1i3. На выходе второго сверху накопителя 19 (фиг. 8) получается сумма b01˙1 + b11˙X1i + b21X1i2. На выходе последнего сверху накопителя 19 получается b0M˙1 и это значение последним выводится из (М + 4)-го регистра на вход 184 выходного накопителя 19, на вход 185 которого поступает из (М + 3)-го регистра 10 последовательность 1, X2j, X2j2, X2jM. С выходов 183 и 194 синхронно поступают вышеуказанные накопленные суммы на входы 184 и 185, обеспечивая получение суммы произведений, аналогичных 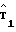 ,
, 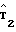 ,
, 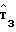 ,
, 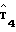 указанным для М 3.
указанным для М 3.
На выходе 189 образуются восстановленные по регрессионной модели значения 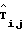 , поступающие на блок 11 формирования корректирующих данных. Блок формирования корректирующих данных (фиг. 9) из значений
, поступающие на блок 11 формирования корректирующих данных. Блок формирования корректирующих данных (фиг. 9) из значений 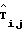 и Тij, поступающих из сдвигового регистра 10 (фиг. 1) на вход 45, формирует разности
и Тij, поступающих из сдвигового регистра 10 (фиг. 1) на вход 45, формирует разности 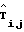 Tij, представляющие собой корректирующие данные. Эти данные, выводимые по второму выходу системы (выход 50 на фиг. 1), дополнительно к коэффициентам bkl регрессионной модели, выводимым по выходу 30, позволяют точно восстановить исходные данные Tij. Инвертор 23 на фиг. 9 служит для подготовки значения Tij к вычитанию на сумматоре 16, причем знаковый разряд числа Тij поступает на отдельный вход 198 сумматора. Местный синхронизатор, выполненный на регистре 18, обеспечивает выдачу корректирующих данных синхронно с серией управляющих сигналов С1.
Tij, представляющие собой корректирующие данные. Эти данные, выводимые по второму выходу системы (выход 50 на фиг. 1), дополнительно к коэффициентам bkl регрессионной модели, выводимым по выходу 30, позволяют точно восстановить исходные данные Tij. Инвертор 23 на фиг. 9 служит для подготовки значения Tij к вычитанию на сумматоре 16, причем знаковый разряд числа Тij поступает на отдельный вход 198 сумматора. Местный синхронизатор, выполненный на регистре 18, обеспечивает выдачу корректирующих данных синхронно с серией управляющих сигналов С1.
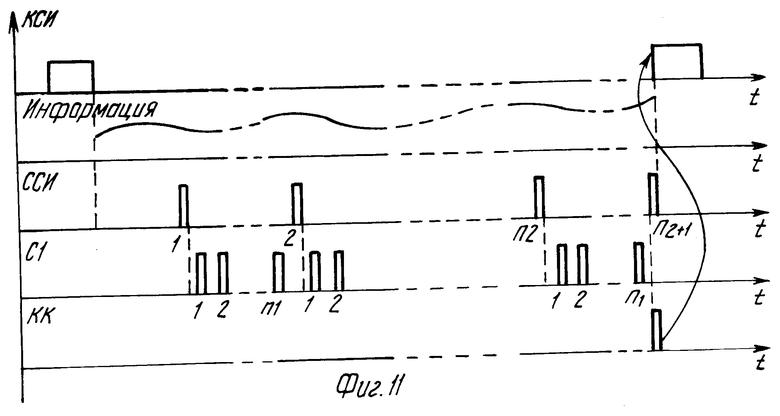
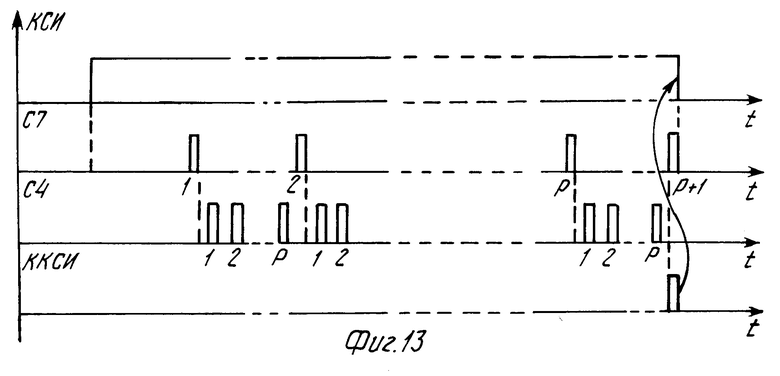
Синхронизация работы всей системы осуществляется блоком синхронизации (фиг. 10). Временная диаграмма представлена на фиг. 11-13. Основными сигналами управления системой являются кадровый синхроимпульс КСИ (вход 51) и строчный синхроимпульс ССИ (вход 52), а также сигналы ККСИ (конец кадрового синхроимпульса) и КК (конец кадра).
Особенностью синхронизации системы является наличие двух генераторов 21 и 22 тактовых импульсов ТИ1 и ТИ2, причем генератор ТИ1 обеспечивает формирование управляющих сигналов С1, С12, С3, С5, а генератор с другой тактовой частотой ТИ2 обеспечивает управляющие сигналы С4 и С7. Второй особенностью синхронизации работы системы является то, что период следования кадров информации содержит два участка: рабочую часть кадра, в течение которой производится передача информации от источника на вход дискретизатора (КСИ 0), и паузу (КСИ 1).
В течение рабочей части кадра формируются управляющие серии С1, С12, С3, С5, обеспечивающие формирование значений правых частей dklнормальной системы, соответствующих (R + 1)-му кадру. Одновременно с вводом данных (R + 1)-го кадра формируются значения корректирующих данных R-го кадра, которые вместе с коэффициентами модели выводятся из системы. В течение паузы формируются значения коэффициентов bklрегрессионной модели (R + +1)-го кадра на основании ранее вычисленных значений dkl. Задержка от начала ввода данных в устройство до начала вывода коэффициентов модели и корректирующих данных равна периоду следования кадровых импульсов. Полностью все сжатые данные выведены спустя время, равное сумме длительности периода следования КСИ и длительности рабочей части кадра КСИ 0.
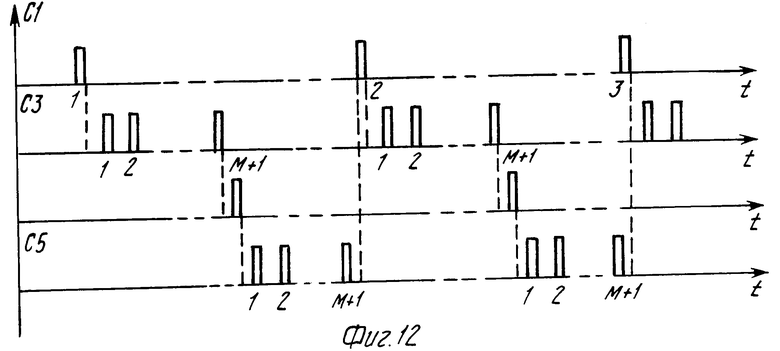
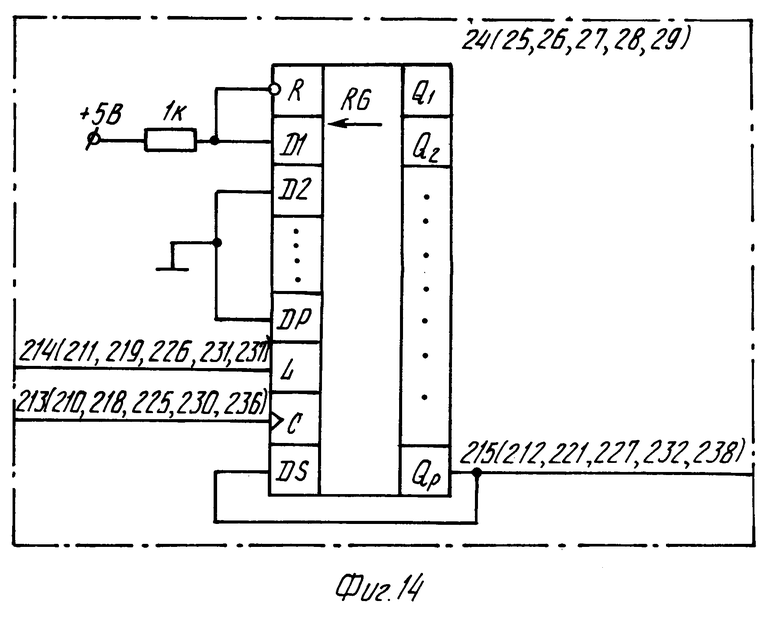
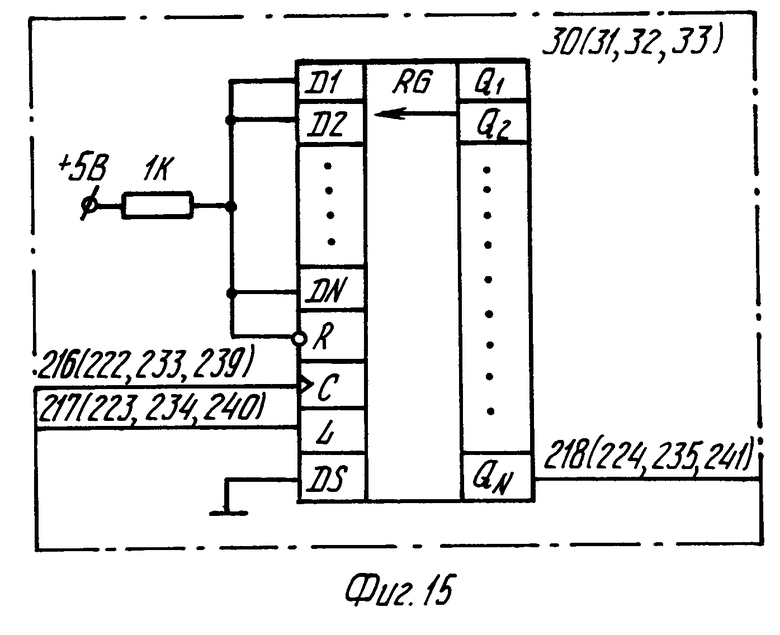
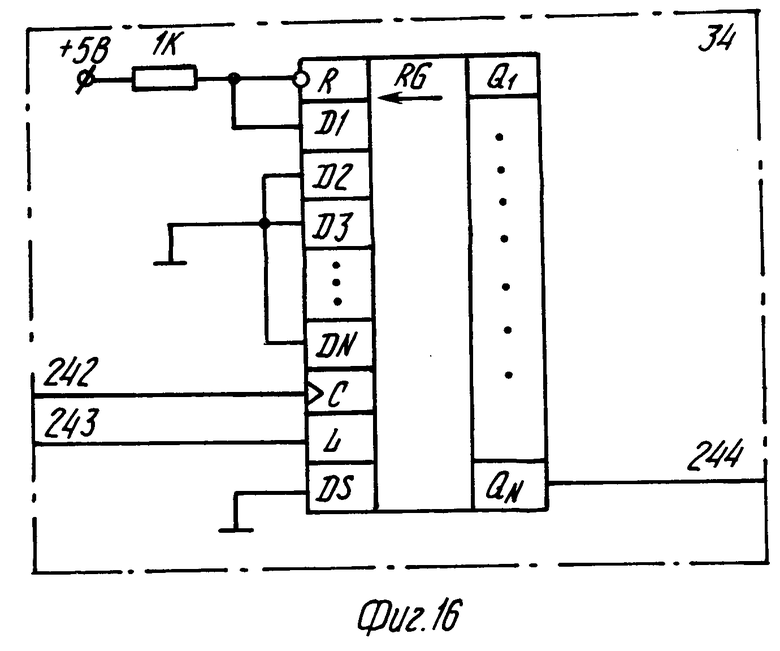
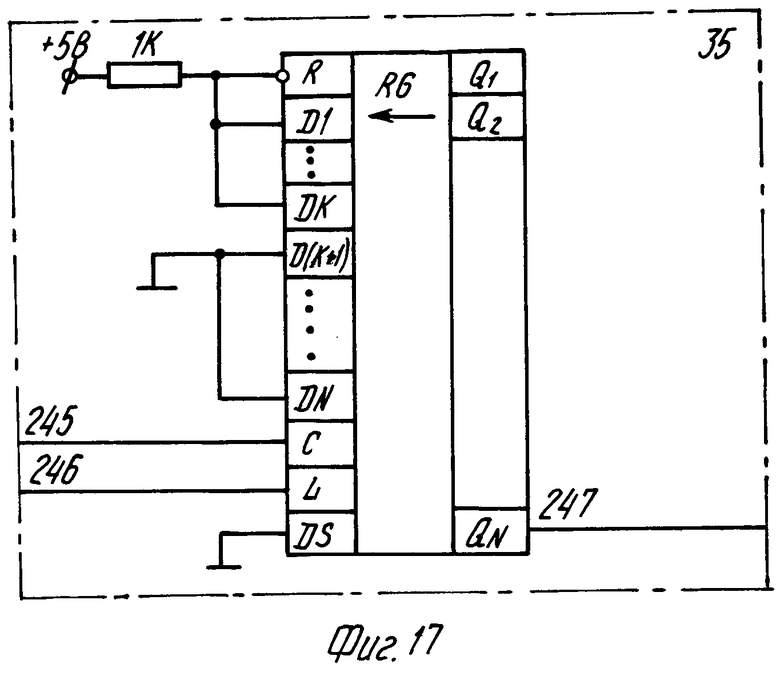
В синхронизаторе (фиг. 10) используются делители частоты 24 по модулю 4, 25 по модулю 4Р, 26 по модулю Р + 1, 27 по модулю n2+1, 28 по модулю (2М+3) n1 и 29 по модулю 2М + 3. Все делители имеют один вход сброса и один счетный вход. Делители могут быть выполнены по схеме фиг. 12 и представляют собой кольцевые регистры, в которые записывается одна "1" подачей сигнала на вход L, а импульсы счета подаются на вход синхронизации сдвига С. Регистры 30-35, формирующие необходимые управляющие последовательности (фиг. 15-17), построены на однотипных элементах и отличаются только числом разрядов и подключением ортогональных входов к уровню логической "1" или "0". Генераторы 22 и 23 синхронизируются по входам 208 и 206 кадровым синхроимпульсом. Синхронизатор формирует следующие серии сигналов (в скобках указаны выходы на фиг. 10): ТИ1 (58), ТИ2 (61), КК (59), ККСИ (62), С1 (56), С3 (53), С12 (60), С4 (54), С5 (55), С7 (57).
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для сжатия двумерных массивов информации | 1987 |
|
SU1497620A1 |
| ТЕЛЕВИЗИОННЫЙ КООРДИНАТНЫЙ ДИСКРИМИНАТОР | 1996 |
|
RU2139640C1 |
| ТЕЛЕВИЗИОННЫЙ КООРДИНАТНЫЙ ДИСКРИМИНАТОР | 1996 |
|
RU2143182C1 |
| УСТРОЙСТВО ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОШИБОК В КАНАЛЕ | 2001 |
|
RU2192038C1 |
| УСТРОЙСТВО ДЛЯ ОЦЕНКИ СТЕПЕНИ ОПТИМАЛЬНОСТИ РАЗМЕЩЕНИЯ | 2000 |
|
RU2177172C1 |
| АКУСТОЭЛЕКТРОННОЕ УСТРОЙСТВО ОБРАБОТКИ СИГНАЛОВ | 1990 |
|
RU2020508C1 |
| УСТРОЙСТВО ДЛЯ ОЦЕНКИ КАЧЕСТВА РАЗМЕЩЕНИЯ | 2000 |
|
RU2171493C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ СУБОПТИМАЛЬНОГО РАЗМЕЩЕНИЯ И ЕГО ОЦЕНКИ | 2001 |
|
RU2193796C2 |
| УСТРОЙСТВО ДЛЯ РАСПОЗНАВАНИЯ СИТУАЦИЙ | 1999 |
|
RU2168207C1 |
| УСТРОЙСТВО ДЛЯ СИНХРОНИЗАЦИИ ПО ЦИКЛАМ | 2003 |
|
RU2231228C1 |

Система для сжатия двумерного массива информации относится к автоматике, телемеханике и вычислительной технике, в частности к обработке дистанционных (например, спутниковых) измерений. Целью изобретения является сокращение избыточности передаваемой информации, отображающей сложные немонотонные двумерные зависимости и содержащей случайную составляющую. Система содержит блок 8 формирования сжатых данных, блок 9 восстановления, сдвиговый регистр 10 и блок 11 формирования корректирующих данных, причем выходы блока 4 сокращения избыточности соединены с групповым входом блока 8 формирования сжатых данных. Введение в состав системы блока формирования сжатых данных, блока восстановления и блока формирования корректирующих данных позволяет до передачи данных произвести восстановление числового массива по сжатой информации, вычислить корректирующий массив разностей элементов исходного и восстановленного массива и передать не только массив сжатых данных, но и этот корректирующий массив разностей. Введение в блок сокращения избыточности М + 1-разрядного регистра, умножителя и М + 1 формирователей группы правых частей нормальной системы обеспечивает сжатие двумерных числовых массивов информации, отображающих сложные немонотонные зависимости, так как в блоке сокращения избыточности реализована регрессивная модель сжатия M-го порядка (M ≥ 2). 9 з. п. ф-лы, 1 табл. 18 ил.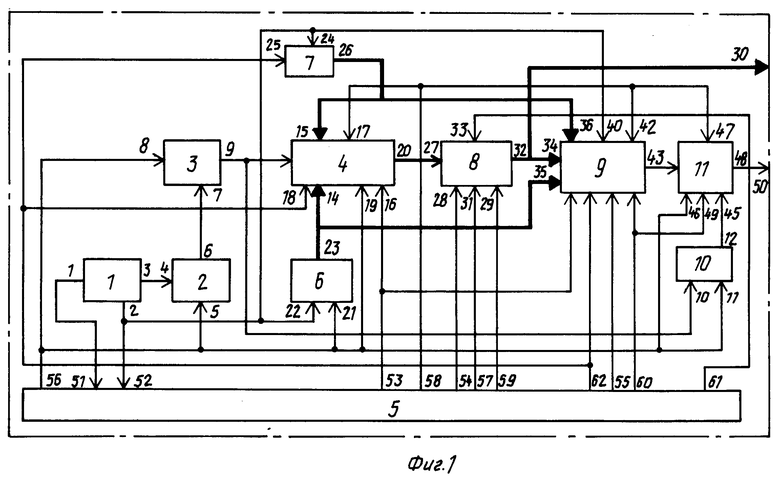
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Устройство для сжатия двумерных массивов информации | 1987 |
|
SU1497620A1 |
| Топка с несколькими решетками для твердого топлива | 1918 |
|
SU8A1 |
| Механизм для сообщения поршню рабочего цилиндра возвратно-поступательного движения | 1918 |
|
SU1989A1 |
Авторы
Даты
1995-10-20—Публикация
1993-02-26—Подача