Изобретение относится к методам исследования тонких пленок и поверхности твердого тела, в частности адсорбированных слоев, находящихся в равновесии с газовой фазой при высоких давлениях.
Известен прибор [1] названный сканирующим туннельным микроскопом (СТМ), и способ его использования для исследования поверхности твердого тела. Объект, представляющий собой проводящую поверхность, располагают в непосредственной близости от острия из проводящего материала, служащего зондом СТМ, так, что через пространственный промежуток зонд поверхность (туннельный зазор) могут туннелировать электроны. Зонд СТМ устанавливают над исследуемой областью поверхности. Обратная связь прибора обеспечивает поддержание во время измерений постоянным одного из параметров, характеризующих туннельный зазор, например, туннельного тока, что при постоянстве напряжения между зондом и проводящей поверхностью объекта эквивалентно стабилизации величины туннельного зазора. Измеряемой величиной обычно является профиль поверхности, который получается в результате сканирования зондом по образцу. Сильная зависимость туннельного тока от величины зазора обуславливает высокую чувствительность прибора к изменению положения зонда по вертикали, а наряду с дополнительными техническими приспоосблениями, обеспечивает высокое (атомарное) разрешение СТМ как по вертикали, так и в плоскости образца. Образец и туннельный зазор располагают в вакууме. Измерения проводят при небольших напряжениях на зонде относительно образца, т.е. в туннельном режиме, при этом величина зазора составляет всего несколько десятых нм. Это обеспечивает высокое пространственное разрешение, однако ограничивает возможности исследования непроводящих объектов со значительно большими размерами по вертикали.
Описан (Янг, Уорд, Скайнер // Приборы для научных исследований. 1972, N 7, с. 36) прибор, названный топографайнером, и способ его применения для исследования профиля поверхности проводящего образца. Объект располагают в непосредственной близости от зонда прибора, через который течет автоэмиссионный ток, формирующийся за счет туннелирования через потенциальный барьер вблизи поверхности острия. Зонд располагают над исследуемой областью поверхности образца. Высокие напряжения на зонде обуславливают эмиссионный режим работы прибора. Величины зазора зонд поверхность проводящего образца варьируют в очень широких пределах, однако топографайнер не может устойчиво работать вблизи туннельного режима (малые величины зазора и напряжения на зонде), что в частности обуславливает меньшее пространственное разрешение, чем в случае СТМ. Измерения также проводят в вакууме, попытки работать в газовой среде с высоким давлением оказались безуспешными.
Прогресс в развитии СТМ привел к возможности выполнения работ с его применением не только в вакууме, но и в газовой среде, в частности на воздухе. Описано [2] исследование при атмосферном давлении адсорбированного слоя атомов серы на поверхности молибдена, который помещают в туннельный зазор СТМ, устанавливают зонд над исследуемой областью и сканируют зондом по поверхности образца, определяя таким образом пространственное расположение атомов серы. Измерения проводят в туннельном режиме (напряжение зонд образец 21 мВ).
С помощью СТМ можно измерять не только пространственные характеристики объектов, но и электронные параметры материала поверхности. Этот способ диагностики, называемый растровой туннельной спектроскопией [3] выбран в качестве прототипа, совпадающего с предлагаемым изобретением по большинству существенных признаков. В соответствии с ним объект помещают в туннельный зазор СТМ, устанавливают зонд над исследуемой областью поверхности объекта, фиксируют ширину туннельного зазора (путем рамызкания на время цепи обратной связи), сканируют напряжением U на туннельном зазоре и одновременно измеряют туннельный ток. Такие измерения можно проводить в каждой точке поверхности образца, что дает локальные зависимости 1(U). Локальная плотность электронных состояний затем вычисляется с использованием полученных экспериментальных зависимостей. Сканирование напряжением U проводят в узком диапазоне значения вблизи нуля (от -3 до +3 В), практически СТМ при этом работает в туннельном режиме. При исследовании таким способом слоев с плохой проводимостью на проводящей подложке их толщины ограничены несколькими монослоями.
Изобретение направлено на обеспечение возможности локальной диагностики с помощью СТМ относительно толстых слоев с плохой проводимостью (диэлектриков) на проводящих подложках. Такими объектами, например, являются адсорбированные слои, находящиеся в равновесии с парами соответствующего вещества, при высоких давлениях и низких температурах поверхности. В частности, такая ситуация возникает в естественных условиях при атмосферном давлении, когда на большинстве поверхностей образуются толстые адсорбированные слои, состоящие из молекул воды и газов воздуха. Аналогичные условия могут быть, например, при использовании металлов в качестве катализаторов в среде газообразных реагентов. Возможность экспериментально исследовать адсорбированные слои, находящиеся в равновесии с газовой фазой при высоких давлениях, особенно ценна в связи с тем, что большинство известных экспериментальных методов изучения поверхности и процесса адсорбции требует высокого и сверхвысокого вакуума, что часто бывает достаточно далеко от реальных условий существования и использования таких слоев.
Поставленная задача решается тем, что в известном способе, в котором объект помещают в туннельный зазор СТМ, устанавливают зонд СТМ над исследуемой областью поверхности объекта, сканируют напряжением U на туннельном зазоре и одновременно измеряют величину, характеризующую состояние туннельного зазора, а затем вычисляют параметры слоя, ряд операций выполняют в особых условиях, а именно: сканирование напряжением при условии стабилизации туннельного тока проводят в диапазоне U, охватывающем, или эмиссионный, или как туннельный, так и эмиссионный режимы работы СТМ, во время сканирования измеряют величину туннельного зазора, а параметры слоя вычисляют, используя один или несколько из характерных элементов зависимости величины зазора от напряжения U. Кроме того, в качестве характерных элементов зависимости величины зазора от напряжения U берут: напряжение U=Uкр, соответствующее скачку величины зазора в сторону меньших значений при уменьшении U, величину скачка зазора при напряжении U=Uкр, наклон линейного участка при U>Uкр, наклон линейного участка при напряжении U<Uкр, значение напряжения U=Uос, соответствующее середине области неустойчивости, разницу величин зазора при напряжении на зонде вблизи О В и минимальной величины зазора при U=Uкр. Кроме того, при сканировании напряжением U измеряют разность величины зазора при постоянном значении напряжения Uo из диапазона сканирования и текущем значении напряжения U, при этом каждый шаг сканирования включает выполнение последовательных операций: установку постоянного значения напряжения Uо, измерение соответствующего значения зазора, изменение напряжения на туннельном зазоре до текущего значения U, измерение нового значения зазора, вычисление разности величин зазоров. Кроме того, время от начала изменения напряжения Uo до начала измерения нового значения зазора выбирают минимальным, но большим времени завершения переходного процесса в СТМ. Кроме того, значение напряжения Uo берут максимальным из диапазона сканирования.
В источниках информации не обнаружено сведений аналогичных предложенному способу диагностики диэлектрического слоя на проводящей поверхности, что позволяет сделать вывод о его новизне.
Кроме того, совокупность признаков предлагаемого способа неочевидна для специалиста из достигнутого уровня техники для решения поставленной задачи, что подтверждает соответствие способа критерию "изобретательский уровень".
Обоснование предлагаемого способа вместе со сведениями, подтверждающими возможность его осуществления, приводятся ниже с использованием графических материалов.
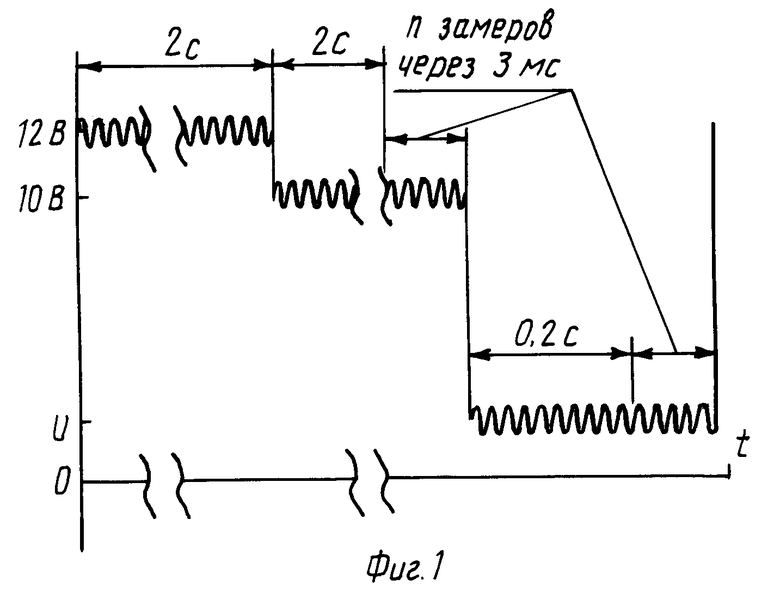
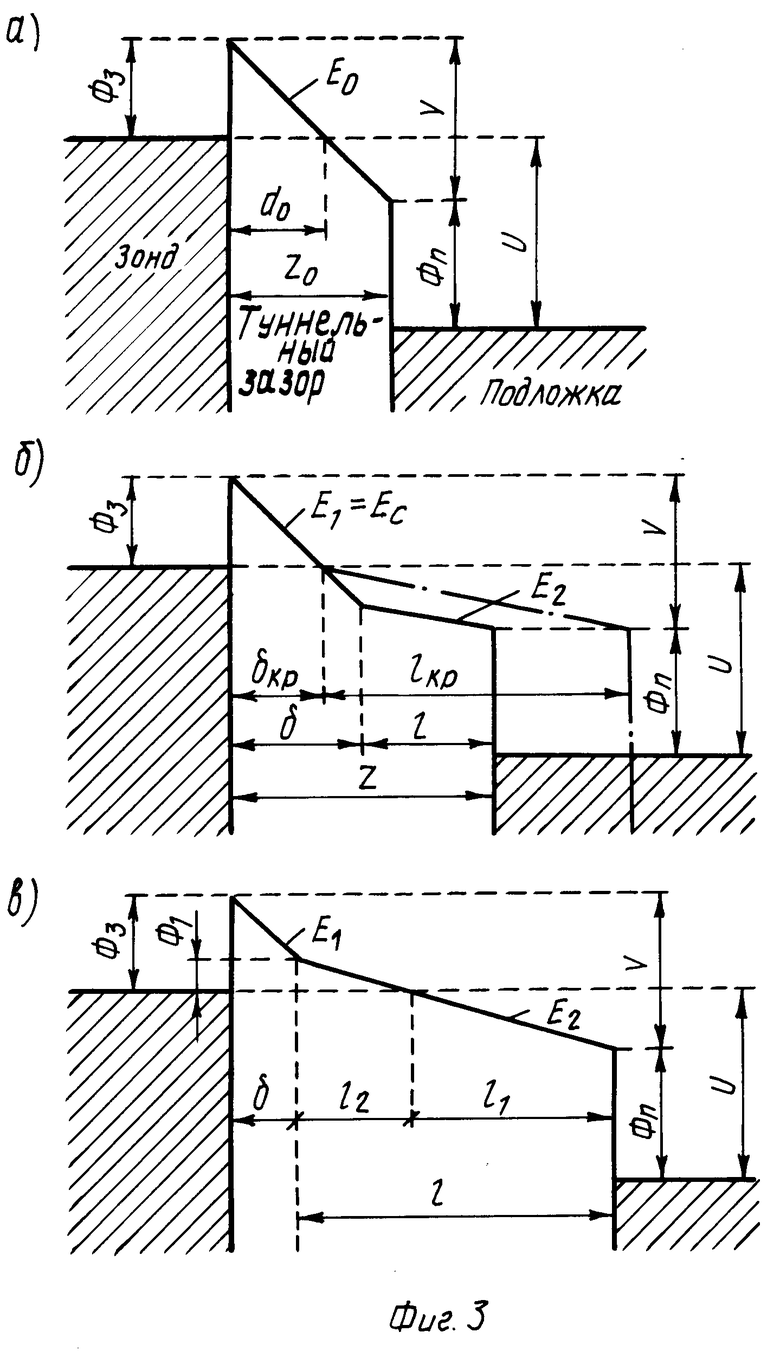
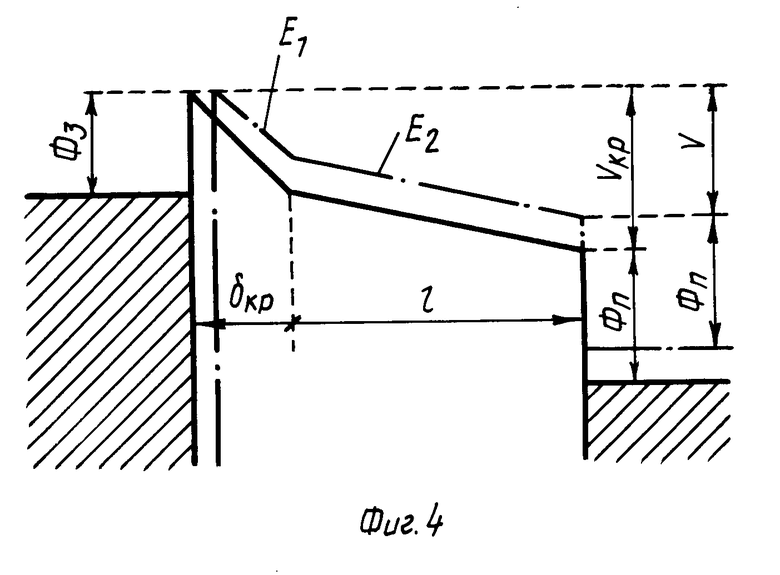
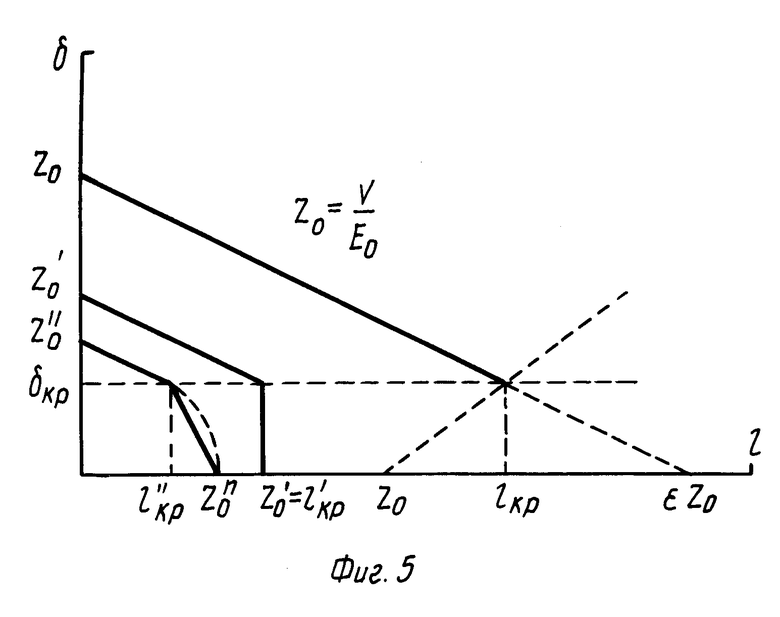
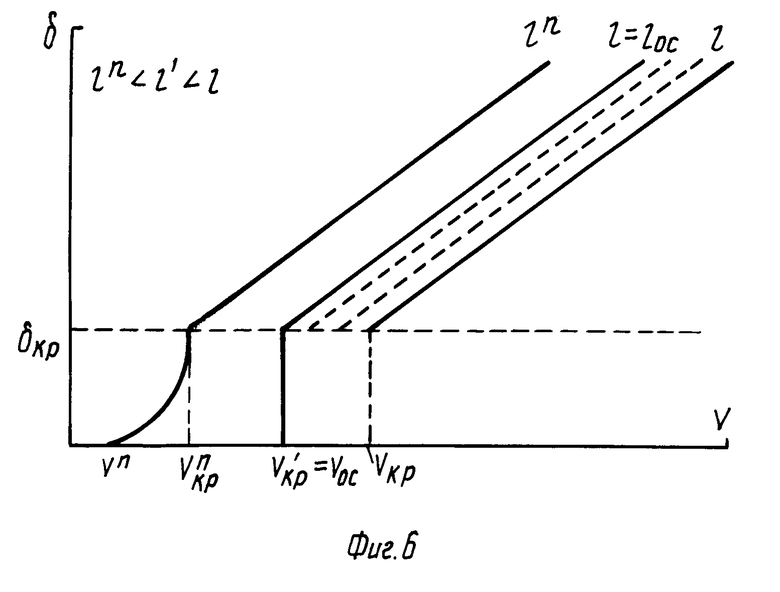
На фиг. 1 изображена временная диаграмма одного шага измерения изменения Δ Z величины туннельного зазора при изменении напряжения на зазоре от 10 В до текущего значения U; на фиг. 2 экспериментальная зависимость величины изменения зазора Δ Z, а также среднего квадратичного отклонения величины Δ Z, от напряжения U; на фиг. 3 потенциальные диаграммы туннельного зазора: при отсутствии в зазоре диэлектрической пленки (а), при наличии в зазоре диэлектрической пленки толщиной l ≅ lкр (б), при наличии в зазоре диэлектрической пленки толщиной l>lкр (в); на фиг. 4 потенциальная диаграмма туннельного зазора при наличии в зазоре диэлектрической пленки и условии U ≅ Uкр; на фиг. 5 теоретические зависимости величины свободного зазора δ от толщины l диэлектрической пленки; на фиг. 6 теоретические зависимости величины свободного зазора δ от напряжения U на туннельном зазоре; на фиг. 7 теоретическая зависимость величины изменения зазора Δ Z от напряжения на туннельном зазоре U; на фиг. 8 потенциальные диаграммы туннельного зазора при наличии адсорбированного слоя и на образце и на острие зонда: при значениях U>Uкр (а), при значениях U<Uкр (б).
Измерения выполнялись на СТМ с электромагнитным сканером, который описан в статье (Корняков Н.В, Левин В.Л. Макаров Е.Б. Мордвинцев В.М. // Электронная техника. Микроэлектроника. 1991, 1, с. 3). В качестве объекта служила тонкая металлическая пленка сплава W-Ti (10% Ti) толщиной около 50 нм, напыленная ионно-плазменным распылением на кремниевую пластину. Эксперимент проводился на воздухе в естественных условиях обеспыленных помещений, в которых образец выдерживался в течение нескольких дней. При этом на поверхности металлической пленки образовывался обычный для таких условий адсорбированный слой из молекул воды и газов воздуха. В качестве зонда использовалось вольфрамовое острие, полученное из проволоки диаметром 0,5 мм электрохимическим травлением. Острие искусственно затуплялось, чтобы обеспечить условие однородного электрического поля в зазоре.
Объект помещался в зазор СТМ, и при визуальном контроле в микроскоп зонд устанавливался над произвольно выбранной исследуемой областью поверхности.
Сканирование напряжением U на туннельном зазоре в диапазоне от 0 до 10 в и измерение при этом величины зазора выполнялось специальным образом. Некоторые особенности прибора (частота первого механического резонанса сканера была около 560 Гц), а также то, что он работал в эмиссионном режиме на воздухе, приводили к высокому уровню шумов. Поэтому для получения надежных данных приходилось прибегать к большому числу измерений каждого значения и последующему их усреднению. Это, в свою очередь, приводило к большим временам снятия зависимости величины зазора от напряжения U, и обуславливало необходимость принятия специальных мер для борьбы с тепловыми дрейфами прибора. В связи с этим эксперимент был организован следующим образом. Прибор работал в режиме стабилизации туннельного тока. Измерялась разность координат положения зонда после прыжка напряжения на нем с 10 В до заданного значения U. На фиг. 1 приведена временная диаграмма одного шага такого измерения. Зонд выдерживался 2 с при напряжении на нем 12 В. Эмпирически было установлено, что такая процедура, т.е. начало цикла измерения с максимальных значений диапазона сканирования, приводит к заметному уменьшению уровня шумов при последующих измерениях. Далее скачком напряжение на зонде менялось до 10 В и после двухсекундной выдержки выполнялся 31 замер координаты зонда Z10 через 3 мс, значения Z усреднялись. Напряжение скачком уменьшалось до заданного U, и после выдержки 200 мс, которая необходима для того, чтобы в системе завершились переходные процессы, выполнялся 31 замер новой координаты ZU. После чего процесс повторялся. Таким образом получалась одна пара значений U и Δ Z= Z10-ZU. Для каждого U измерялось 23 значения Δ Z, они усреднялись и вычислялись средние квадратичные отклонения. Прибор был оснащен ЭВМ типа IBM PC, весь эксперимент был автоматизирован. Выдержка после скачка значения напряжения с 10 В до величины U желательна минимальная, чтобы уменьшить величину дрейфа характеристик прибора между измерениями и минимизировать общее время измерений, но она должна быть больше времени завершения переходного процесса в СТМ, поскольку иначе будут измерены искаженные значения величины зазора и потребуется дополнительная математическая обработка. При использовании более совершенного прибора, обеспечивающего приемлемый уровень шумов, такой сложный способ сканирования по напряжению U и измерения зазора может не потребоваться. Применение же этого способа позволяет получить удовлетворительные результаты и в условиях высоких шумов и дрейфов.
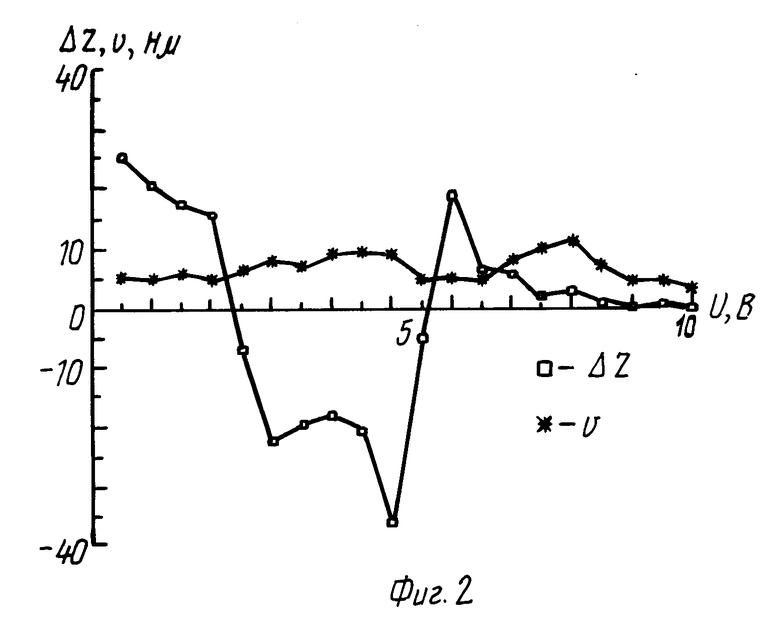
На фиг. 2 показана экспериментальная зависимость изменения величины зазора Δ Z от напряжения на туннельном зазоре U. Она имеет вполне определенные характерные элементы, которые можно использовать для вычисления параметров адсорбированного слоя. В частности, наблюдается скачек величины зазора в сторону меньших значений (на фиг. 2 вверх) при уменьшении напряжения U, и область неустойчивости, в которой зазор значительно увеличен по сравнению с плавным ходом кривой. Для вычисления по характерным элементам этой зависимости параметров адсорбированного слоя должна быть построена модель системы "туннельный зазор СТМ с диэлектрической пленкой", из которой будет ясно, почему и как можно использовать зависимость фиг. 2 для этих целей. Ниже приводятся такие модели и результаты конкретных вычислений.
На фиг. 3 (а) приведена потенциальная (она эквивалентна энергетической) диаграмма туннельного зазора без диэлектрической пленки при напряжении на зонде U и работах выхода из зонда и подложки соотетственно Фз и Фп (в вольтах). Определения используемых величин ясны из фиг. 3. Напряжения U и V связаны соотношением
V=U+Фз-Фп (1)
Эмиссионному режиму соответствует условие U>Фп, при этом электроны, туннелируя через барьер, попадают в область зазора. В туннельном режиме U<Фп и электроны туннелируют непосредственно в зону проводимости металла подложки. Туннельный ток в таких условиях можно записать в виде (Роуэлл Дж.М. // Туннельные явления в твердых телах. М. Мир, 1973, с. 369)
It= АФ'exp(-Bdф' 1/2), (2) где Ф' средняя высота барьера; d ширина барьера, А и В в первом приближении константы.
Для эмиссионного режима (он показан на фиг. 3 (а)) Ф'=Фз/2, a d=dp= Ф3/Eo, где Eo напряженность электрического поля в зазоре, которая графически отображается наклоном соответствующего отрезка прямой. Тогда
It= Ioexp(-B'Ф3/2/Eo), (3) где Io и B' константы. Здесь важно, что ток зависит только от величины напряженности поля вблизи поверхности зонда. В нашем случае
Eo= V/Zo, (4) где Zo величина туннельного зазора. Т.е. принимается условие однородности поля в пределах эмиттирующего участка поверхности зонда, что эквивалентно условию Zo<<r, где r радиус кривизны острия. Практически это часто выполняется, поскольку типичные значения r 50 нм и более. Если при функционировании СТМ стабилизируется туннельный ток It, то Eo=Eo(It) и остается постоянной в ходе всего эксперимента, т.е. Eo и do некоторые характерные для данного значения тока величины. Тогда в силу (4) Zo линейно зависит от напряжения на зонде U.
На фиг. 3 (б) приведена потенциальная диаграмма при наличии в зазоре диэлектрической пленки толщиной l. Целью решения задачи является выяснение равновесного значения свободного зазора δ а также расстояние зонд-подложка (т. е. зазора) Z, при изменении величин U и l в условиях стабилизации туннельного тока. Считаем, что пленка представляет собой идеальный диэлектрик, в частности, в ней отсутствует захват электронов, прошедших барьер, на локализованные состояния. Такой объект будет описываться следующей системой уравнений:
E1 δ +E2 l= V; E2=E1/ ε E1=E0, (5) где E1 и Е2 напряженности поля на соответствующих участках туннельного зазора, ε относительная диэлектрическая проницаемость материала пленки. Последнее равенство следует из условия постоянства туннельного тока при изменении l, в том числе и до значения l=0. Т. е. оно означает неизменность величины и формы барьера, через который туннелируют электроны. Решение этой системы уравнений с учетом (4) дает
δZo-l/ εV/E0-l/ε (6)
В координатах (δ l) эта зависимость изображается (см. фиг. 4) прямой, отсекающей на оси δ отрезок Zo, а на оси l отрезок ε Zo.
Однако, уравнение (6) не описывает поведение системы "туннельный зазор СТМ с диэлектрической пленкой" при всех значениях l. Как видно из фиг. 3 (б), с ростом l достигается критическое положение (показано штрих-пунктиром), после которого начинает меняться форма барьера для туннелирующих электронов. В критической точке
δкр=d0=Ф3/E0; lкр= ε(V-Ф3)/Eo=
ε Zo(1-Ф3). (7)
При l>lкр система уравнений (5) перестает быть справедливой, потенциальная диаграмма для этого случая показана на фиг. 3 (в). Барьер для туннелирующих электронов здесь состоит из двух участков ( δ и l2) с различными напряженностями поля.
Мы принимаем, что условие стабилизации туннельного тока при l>lкр эквивалентно постоянству ширины составного барьера на фиг. 3 (в)
δ +l2= δкр=d0. (8)
Такая модель точно соответствует реальности в крайних точках (l2=0 и δ0) и завышает прозрачность барьера в остальных положениях. Ниже будет показано, как отразится такое приближение на результатах. Совместное решение (8) и системы уравнения, следующих из фиг. 3 (в)
E1 δ +E2l=V; E1δ +E2l2=Ф3;
l1+l2=l; E2=E1/ε (9) дает линейную зависимость δ от l:
δ(l-Z0)/[ γ (ε -1)-ε (10) где γV/Ф3.
На фиг. 5 показаны получающиеся из (6) и (10) кривые δ (l) при различных значениях напряжения на зонде V, соответствующих различным Zo. Для малых V (значение Zo" на фиг. 5, при этом знаменатель в (10) меньше 0) с ростом l при критической толщине диэлектрика (см. (7)) происходит просто изменение наклона прямой. Как легко показать, этот новый наклон не может быть меньше 1, т.е. свободный зазор на этом участке уменьшается значительно быстрее, чем на начальном, и становится равным нулю точно при равенстве l=Zo". Таким образом, когда с ростом l зонд упирается в диэлектрическую пленку, зазор оказывается равным точно величине, соответствующей зазору в отсутствии пленки (правильнее сказать величине, соответствующей однородному по ε материалу в зазоре, поскольку Zo не зависит от ε, а определяется только напряженностью поля). С дальнейшим ростом l зазор не меняется, т.е. происходит вдавливание иглы зонда в материал диэлектрика. Если не принимать приближения (8), то характер зависимости δ на участке от lкр" до Zo" будет соответствовать кривой, показанной пунктиром, поскольку реально прозрачность барьера для туннелирующих электронов должна быть несколько ниже. Это, однако, не меняет основных выводов модели. На фиг. 6 приведено семейство зависимостей δ (V) для различных толщин диэлектрической пленки. При малых l (значение l") кривая на различных участках описывается формулами (6) и (10). Этот случай также соответствует плавному изменению δ. Перегиб кривой происходит при критическом значении напряжения на зонде, определяемом из (7)
Vкр=lEo/ ε +Ф3, (11)
при подстановке l=l". Как легко показать, используя (10), δ становится равным 0 в точке V"=Eol", а на участке от V" до V"кр зависимость δ (V) описывается гиперболой. По соображениям, аналогичным приведенным выше, реальная кривая на этом участке будет несколько иной, на фиг. 6 она изображена пунктиром.
Качественно по иному ведет себя зазор в случае больших напряжений V на зонде (значение Zo на фиг. 5. при этом знаменатель в (10) больше 0). Возрастающая ветвь при l>lкр не имеет физического смысла, поскольку, как легко показать, ей соответствуют l2<0. Т.е. система уравнений (8) и (9) не имеет физически значимых решений в этой области. Что же должно происходить с величиной зазора в точке l=lкр? На фиг. 6 этой ситуации соответствует крайняя правая зависимость и критическое напряжение на зонде Vкр, даваемое выражением (11). Как легко показать, зонд при этом будет приближаться к поверхности диэлектрической пленки и вдавливаться в нее до достижения величины зазора, равной Zo (фиг. 5). Причем такой характер поведения системы не связан с допущением (8), а имеет более общие причины. На фиг. 4 приведена потенциальная диаграмма, поясняющая механизм этого явления. С уменьшением напряжения на зонде V при заданной толщине пленки достигается критическое значение Vкр (см. фиг. 6), т.е. реализуется ситуация, которой на фиг. 4 соответствует сплошная линия. При дальнейшем уменьшении V (штрих-пунктирная линия на фиг. 4) должны уменьшиться и наклоны прямых, соответствующие напряженностям поля Е1 и Е2, поскольку они жестко связаны друг с другом соотношением, выражаемым последним уравнением в системе (9). Но это означает увеличение ширины барьера при сохранении его высоты, уменьшение туннельного тока It, а значит, в силу вполне определенного способа функционирования обратной связи СТМ, приближение зонда к проводящей поверхности образца до того момента, пока It не станет равен стабилизруемому значению. Таким образом, при достаточно больших значениях l и V существует область как бы запрещенных значений δ (от Ф3/Еo до 0), которые по достижении критического условия (11) система проскакивает и стабилизируется при величине зазора Zo. Уравнение (10) правильно описывает такое поведение системы, поскольку точка со значениями δ0, l=Zo (см. фиг. 5) является его решением. С дальнейшим уменьшением V зазор Zo уменьшается в соответствии с (4).
Наконец, еще одна особая точка определяется равенством нулю знаменателя в (10), что означает вполне определенную величину V
Vос=Ф3 ε /(ε -1). (12)
Если при этом еще и толща диэлектрической пленки l=l' такова, что V= V'кр=Vкр(l'), то условие Vос=V'кр дает значение
l'=lос=Ф3 ε /( ε -1)/Eo (13)
и возникает особая ситуация, изображаемая на фиг. 5 и 6 средними линиями из семейств. В этой особой точке любое значение является решением уравнения (10), так как l=l'кр(V'кр)=l'кр=Zo, и равен нулю не только знаменатель, но и числитель в (10). Т.е. система "туннельный зазор СТМ диэлектрическая пленка" как бы "не знает" какое положение при этом занять, ей безразлична величина зазора. Поведение реальной системы в такой точке будет определяться некоторым другим более тонким механизмом, который не учитывается в предлагаемой модели. На первый взгляд, отмеченная особая точка кажется слишком специфической, которая практически очень редко реализуется: нужно совпадение условий V= Voc и l=lос. Однако, второе из них выполняется автоматически при достаточно больших толщинах пленки, поскольку после вдавливания в нее зонда l перестает быть независимой величиной, всегда l=Zo(V), т.е. числитель в (10) равен нулю и система находится на границе области, в которой справедливо решение (10). Это хорошо видно на фиг. 5. Поэтому практически только такая ситуация и реализуется, и можно ожидать проявления этой неустойчивости просто на зависимости величины зазора от V. Кроме того, необходимо учитывать, что для наблюдения системы в такой особой точке соответствующие величины не должны обращаться в ноль точно, достаточно, чтобы зависимости на фиг. 5 и 6 были очень круты. При этом особая точка будет "размазываться" в область конечной ширины по V, т.е. реально надо говорить о некоторой области неустойчивости.
Используя полученные результаты, легко получить зависимость экспериментально измеряемой величины Δ Z от напряжения U. Связь величины U и V дается выражением (1) и не вносит заметных корректив в искомую кривую. Далее необходимо учесть, что Z= δ +l U>Uкр Z=Zo U<Uкрю
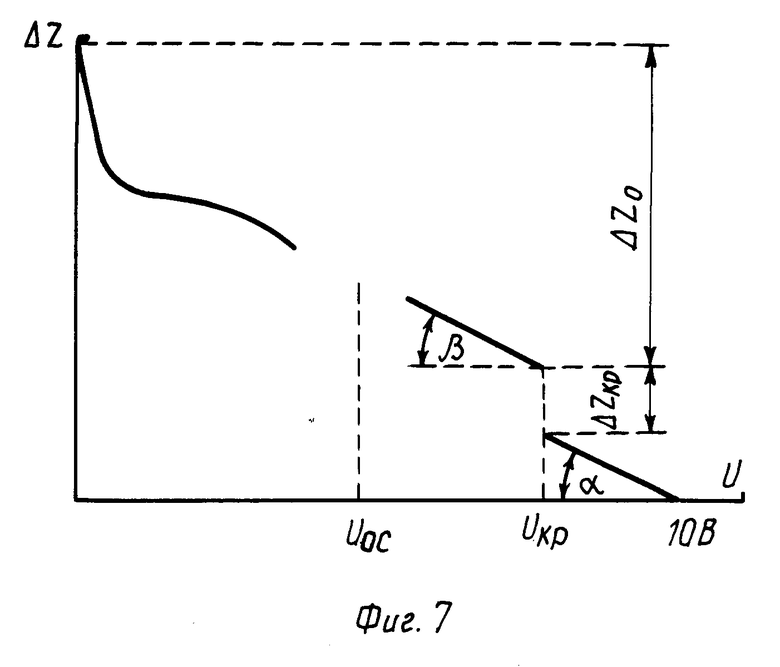
Тогда зависимость Δ Z(U) при условии достаточно больших толщин диэлектрической пленки будет иметь вид, показанный на фиг. 7 (ось Z направлена от поверхности образца наружу). Характерными элементами зависимости величины изменения зазора Δ Z от напряжения U являются: напряжение U=Uкр, соответствующее скачку величины зазора в сторону меньших значений при уменьшении U, величина скачка Δ Zкр зазора при напряжении U=Uкр, наклон α линейного участка при U>Uкр, наклон β линейного участка при напряжении U<Uкр, значение напряжения U=Uос, соответствующее середине области неустойчивости, разница Δ Zo величин зазора при напряжении на зонде вблизи О В и минимальной величины зазора при U=Uкр.
В принятой модели
tg αtg β1/Eo. (14)
Скачок величины зазора при U=Uкр
Δ Zкр= δкр+(l-Zo)=l( ε -1)/ε (15)
Наконец, вблизи Uос возможна некоторая область неустойчивости, поведение системы в которой не описывается предложенной моделью, но само значение U= Uос может служить для определения параметров диэлектрического слоя.
Сравнение фиг. 2 и 7 (при этом надо учитывать, что экспериментальные точки сняты с дискретностью 0,5 В) позволяет определить из экспериментальных данных некоторые значения величин, являющихся, с одной стороны, параметрами предложенной модели, а, с другой стороны характерными элементами зависимости величины зазора от напряжения U Uкр=6 В; Δ Zкр=14 нм; Uос=4 В; tg α1,32 нм/В
(16)
Учитывая близость материалов зонда и поверхности образца по составу, можно принять, что их работы выхода в таких условиях одинаковы: Фз=Фп=Ф тогда U= V. Используя (16) и решая систему уравнений (11), (12), (14), (15), которая сводится к квадратному уравнению, можно получить оценки основных физических параметров, характеризующих адсорбированный слой и туннельный зазор
Eo=I/tg α0,76 В/нм
ε= (D+ 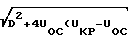 ))/(UКР-UОС)/2= 4,74
))/(UКР-UОС)/2= 4,74
где D=Eo Δ Zкр+Uкр-2Uос;
Ф=( ε -1)Uос/ ε3,16 В;
l= Δ Zкр ε /( ε -1)=17,7 нм.
Разумность полученных величин является дополнительным подтверждением правильности предложенной модели. Параметры ε и l характеризуют собственно адсорбированный слой, Ео и Ф относятся больше к характеристике туннельного зазора, а именно потенциального барьера, через который туннелируют электроды, т.е. несут информацию о взаимодействии адсорбированного слоя с металлической поверхностью.
Таким образом, показано, как используя экспериментальную зависимость фиг. 2 и модель соответствующих процессов, можно определить параметры адсорбированного слоя. Поскольку в модель заложено только общее предположение о диэлектрической природе материала диагностируемого слоя, все сказанное относится к любому диэлектрическому слою, хотя наиболее интересно, конечно, применение способа к адсорбированным слоям, находящимся в равновесии с газовой фазой. Из описанной модели также ясно, что точность определения параметров слоя тем выше, чем больше отличается параметр ε от 1, поскольку в формулы входит разность ( -1). Предполагается также, что материал диэлектрического слоя имеет твердость значительно меньшую, чем материал зонда, что позволяет острию легко вдавливаться в диагностируемый слой. Этому условию удовлетворяют многие материалы, в частности любые органические слои.
Как установлено из приведенных экспериментов, адсорбированный слой очень быстро восставнавливался после вдавливания в него зонда: этот процесс занимал время меньшее, чем несколько секунд, необходимых для одного цикла измерений. Восстановление толщины адсорбированного слоя могло происходить как за счет поверхностной диффузии, так и поступления молекул из объема. Тем не менее, кривая, аналогичная фиг. 2, но снятая в противоположном направлении изменения U (в сторону его увеличения), имела некоторые отличия. Поэтому измерения выполнялись в сторону уменьшения U, чтобы минимизировать возможные эффекты деформации адсорбированного слоя зондом. Это является еще одним аргументом в пользу того, что значение Uo при измерении Δ Z желательно выбирать максимальным из диапазона сканирования.
Кроме рассмотренной модели могут быть и другие, которые дополняют или уточняют друг друга, однако в любом случае они будут использовать характерные элементы экспериментальной зависимости величины зазора от напряжения на нем.
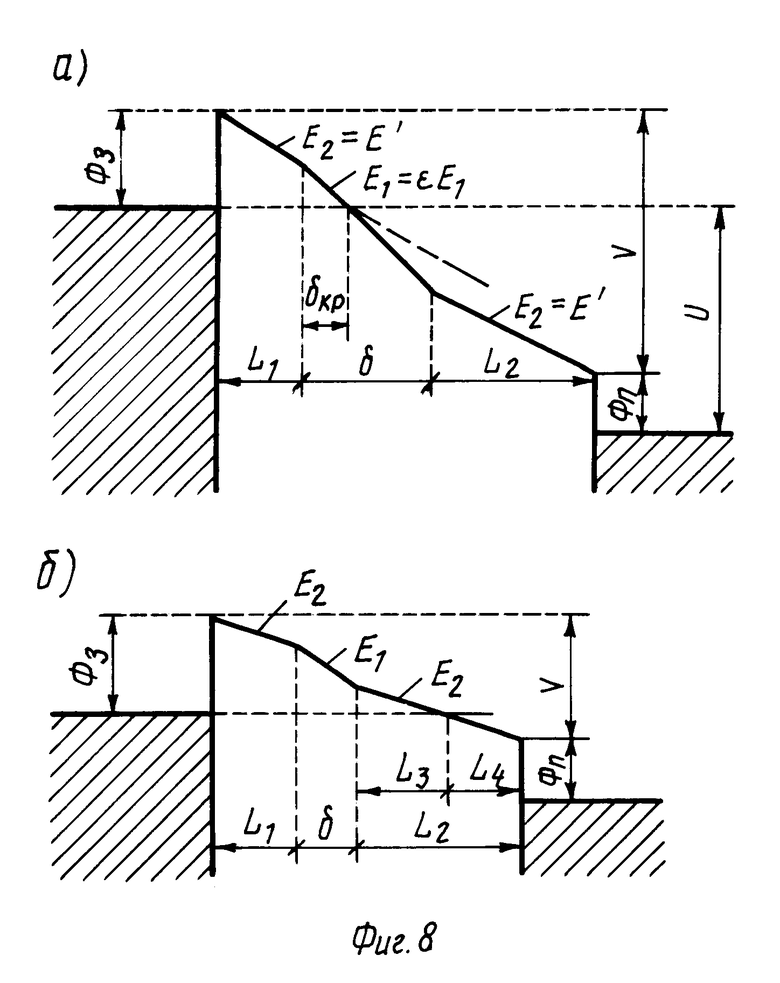
В качестве такого примера рассмотрим модель, которая учитывает возможность наличия такого же адсорбированного слоя не только на образце (его толщина L2), но и на острие зонда (толщина L1). Потенциальная диаграмма этого варианта для малых значений L1 и больших значений U показана на фиг. 8 (а). Путем выкладок, аналогичных приведенным выше, можно получить выражение для свободного зазора
δV/ ε /E'-L/ε (17) где L=L1+L2, E' напряженность поля в адсорбированных слоях. Для случая малых значений U, потенциальная диаграмма которого показана на фиг. 8 (б), записывая для L3, L4, E1 и Е2 систему уравнений, аналогичную (9) и решая ее, получаем
δ(L-Lo)/( γ ( ε -1)-ε ). (18) где Lo= γ (L1+ δкр')
δкр'=(Ф3-E'L1)/ ε /E'. (19)
Таким образом, форма выражений для δ совпадает с аналогичными уравнениями первой модели, а значит и все основные особенности поведения величины зазора в зависимости от напряжения U, будут такими же. Изменятся только некоторые выражения для оценки параметров модели, а поэтому и параметров адсорбированного слоя. Значение поля Е' вблизи зонда определяется из условия Lo= Zo, поскольку в пределе δ->> 0 (18) должно совпадать с (10), откуда для V= Vкр получаем уравнение
(E'L1(ε -1)+Ф3)Vкр/Ф3/ ε /E'= Δ Zo (20)
поскольку после исчезновения свободного зазора (вдавливания зонда в адсорбированный слой) в этой точке Δ Zo=Zo(Vкр). Для напряжения Vкр из фиг. 8 (а) получаем
Vкр=E'L2+Ф3 (21)
Величина скачка зазора при этом Δ Zкр=L2+ δкр'-Zo=L2+(Ф3-E'L1)/ε /E'-Z
(22)
Для величины Uос остается справедливым выражение (12). Из (17) следует, что
tg α=I/ε /E'. (23)
На линейном участке при V<Vкр должно выполняться условие
tgβ I/Eo, (24) поскольку свободный зазор здесь равен нулю и в туннельном зазоре находится однородный по ε материал. На экспериментальной кривой фиг. 2, однако, этот участок отсутствует, и выражением (24) в данном конкретном случае воспользоваться нельзя.
Как и выше, будем считать, что Фз=Фп=Ф, тогда V=U. Решая систему из пяти уравнений (12), (20), (21), (22) и (23), которая тоже сводится к квадратному уравнению, и используя значения (16), а также значение Δ Zo=8 нм (оно получено из фиг. 2 экстраполяцией экспериментальной кривой до оси Δ Z), получаем оценки параметров адсорбированных слоев и туннельного зазора
Ф C/2-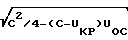 3,16 В где C=( Δ Zкр+ Δ Zo)/tgα
3,16 В где C=( Δ Zкр+ Δ Zo)/tgα
εUос/(Uос-Ф)=4,76;
E'=I/tg α /ε=0,16 В/нм;
L2=(Uкр-Ф)/E'=17,8 нм;
L1= Ф(Δ Zo/Uкр-tg α)=0,04 нм.
Как видно, численные значения совпадают с первым вариантом, а толщина адсорбированного слоя на зонде в данном конкретном случае близка к нулю.
Некоторые из параметров, которые здесь вычисляются, могут быть известны из каких-нибудь предварительных измерений. Тогда для расчета остальных надо брать не все условия, выведенные выше, а только часть или даже одно. При этом конкретные формулы для вычисления могут изменяться, но уравнения соответствующих моделей останутся теми же.
Необходимо обратить внимание на характер поведения величины зазора в области неустойчивости вблизи U= Uос на экспериментальной кривой фиг. 2. Зазор значительно увеличен по сравнению с плавным ходом теоретической кривой, при этом туннельный ток, естественно, стабилизирован на заданном уровне. Это не может и не должно быть объяснено в рамках предложенной модели, но может означать, например, образование проводящих элементов из адсорбата между зондом и подложкой. Как видно из фиг. 2, существует некоторая тонкая структура в поведении Δ Z в области неустойчивости, которая приводит к наличию двух минимумов и локального максимума. Если построить модель, описывающую процессы в этой области напряжений U, можно, очевидно, получить дополнительную информацию об адсорбированном слое. Во всяком случае, отмеченные два максимума и локальный минимум на фиг. 2 тоже могут быть характерными элементами зависимости величины зазора от напряжения на нем.
Таким образом, приведенные выше экспериментальные результаты, а также логические обоснования объясняют смысл существенных признаков изобретения и подтверждают практическую применимость предложенного способа.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЭЛЕМЕНТ УСТРОЙСТВА ПАМЯТИ СО СТРУКТУРОЙ МЕТАЛЛ - ИЗОЛЯТОР - МЕТАЛЛ | 1994 |
|
RU2072591C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРОВОДЯЩЕГО ЭЛЕМЕНТА НАНОМЕТРОВЫХ РАЗМЕРОВ | 2001 |
|
RU2194334C1 |
| ЭЛЕМЕНТ УСТРОЙСТВА ПАМЯТИ СО СТРУКТУРОЙ МЕТАЛЛ-ИЗОЛЯТОР-МЕТАЛЛ | 1997 |
|
RU2108629C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ПОВЕРХНОСТИ МИКРООБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1993 |
|
RU2092863C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТОПОГРАФИИ ПОВЕРХНОСТИ ВЕЩЕСТВА ПОСРЕДСТВОМ СКАНИРУЮЩЕГО ТУННЕЛЬНОГО МИКРОСКОПА | 1992 |
|
RU2072581C1 |
| СПОСОБ ОПЕРАЦИОННОГО КОНТРОЛЯ ИОННО-ЛЕГИРОВАННЫХ СЛОЕВ | 1987 |
|
RU1559983C |
| СПОСОБ ПОЛУЧЕНИЯ НАНОСТРУКТУРЫ "МЕТАЛЛ/ДИЭЛЕКТРИК/ВЫСОКОТЕМПЕРАТУРНЫЙ СВЕРХПРОВОДНИК" | 2001 |
|
RU2197037C1 |
| КОМБИНИРОВАННЫЙ СКАНИРУЮЩИЙ ТУННЕЛЬНЫЙ МИКРОСКОП - РАСТРОВЫЙ ЭЛЕКТРОННЫЙ МИКРОСКОП | 1994 |
|
RU2089968C1 |
| ЯЧЕЙКА МАТРИЦЫ ПАМЯТИ | 2004 |
|
RU2263373C1 |
| ЯЧЕЙКА МАТРИЦЫ ЭНЕРГОНЕЗАВИСИМОЙ ПАМЯТИ | 2005 |
|
RU2302058C2 |
Использование: методы исследования тонких пленок и поверхности твердого тела при помощи СТМ. Сущность изобретения: объект помещают в туннельный зазор СТМ, сканируют напряжением U на туннельном зазоре в диапазоне, охватывающем как туннельный, так и эмиссионный режимы работы СТМ с учетом Uкр соответствующего скачку величины зазора в сторону меньших значений при уменьшении U. 2 з. п. ф-лы, 8 ил.
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Кук Й., Сильверман П | |||
| Приборы для научных исследований, 1989, N 2, с | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1995-11-10—Публикация
1993-03-10—Подача