Изобретение относится к физическим способам анализа размеров частиц и может быть применено в гидрооптике, гидробиологии, биотехнологии.
Известен способ определения размера частиц в суспензии, основанный на измерении показателя ослабления светового потока суспензией на некотором интервале длин волн [1]
Недостатком этого способа является то, что для определения размера частиц требуется знание показателя преломления вещества частиц или их весовой концентрации.
Наиболее близким по технической сущности к предлагаемому является оптический способ определения размеров частиц в суспензии, заключающийся в том, что измеряются показатели ослабления F(θ) светового потока суспензией при двух или более апертурных углах q (угол q пересчитан для среды, в которой взвешены частицы) приемника светового потока, затем рассчитываются отношения F(q)/F(0) и с помощью метода наименьших квадратов сравниваются с теоретическими значениями этого отношения для частиц разных размеров с показателем преломления, равным показателю преломления вещества исследуемых частиц, полученными по теории Ми [2,3] Здесь F(q) и F(0) показатели ослабления светового потока при апертурных углах, равных q и нулю (обычно этот угол равен 30-40 мин) соответственно. И на основании сравнения выбирается наиболее близкая величина размера частиц.
Однако указанный способ трудоемок, требует предварительного знания показателя преломления вещества частиц и применим только для монодисперсных суспензий.
Задачей изобретения является уменьшение трудоемкости определения размеров частиц, расширение границ применимости метода до полидисперсных суспензий и исключение предварительных знаний о частицах.
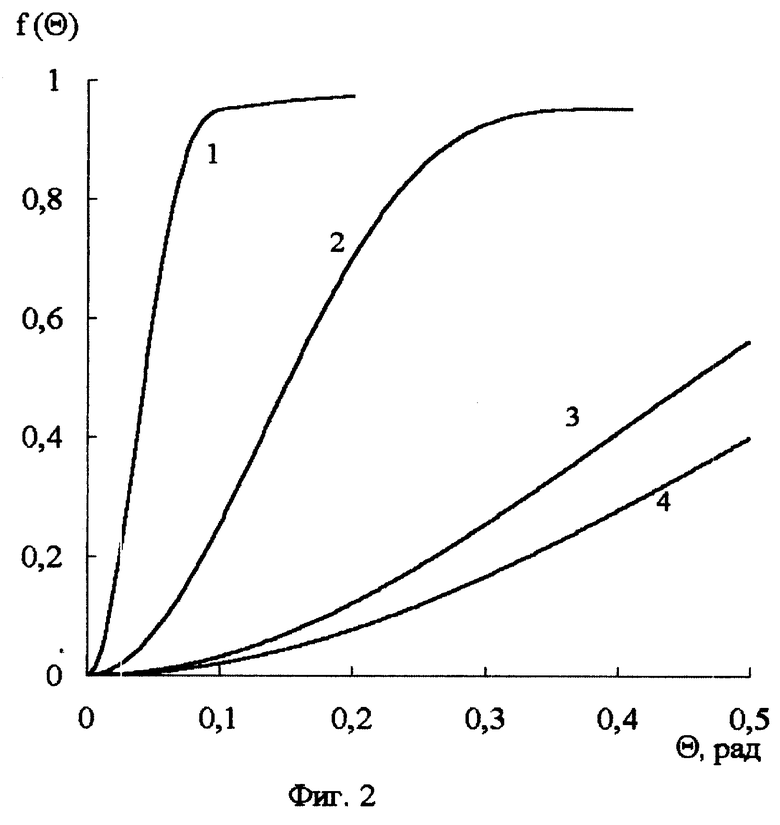
Решение задачи достигается тем, что регистрируется зависимость показателя ослабления F(q) (или показателя рассеяния) светового потока при непрерывном изменении апертурного угла приемника света от 0 до q (интегральная индикатриса), по ней рассчитывается доля светового потока, рассеянного в конус с углом раствора, равным апертурному углу q, и затем по известному алгоритму рассчитывается диаметр d частиц. Сущность этого способа основана на том, что интегральная индикатриса светорассеяния, выраженная в долях света, рассеянного в апертурном угле q, ко всему рассеянному свету для абсолютного большинства монодисперсных взвесей гидрозольных частиц зависит только от произведения дифракционного параметра r частиц на значение апертурного угла приемника светового потока. В то же время доля светового потока, рассеянного в апертурном угле q, для различных r в зависимости от апертурного угла представляет серию кривых с разным углом наклона к оси абсцисс в рабочей области апертурных углов q. Следовательно, если по измеренной интегральной индикатрисе для конкретно выбранной доли светового потока f(q), рассеянной в конусе с углом раствора равным апертурному углу q, находится величина этого угла, а по известной зависимости f(rq) (фиг. 1), находится произведение rq для этой же доли, то подстановкой получаем r и далее диаметр d частиц.
Наиболее точно диаметр определяется, когда доля светового потока, рассеянного в апертурном угле q, равна половине всего рассеянного светового потока. При этом rq 1,8 и дифракционный параметр r равен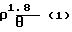
Так как параметр r равен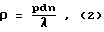
где
n показатель преломления дисперсионной среды суспензии;
l длина волны светового потока в вакууме,
то из (1) и (2) определится диаметр d частиц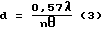
Поскольку форма зависимости f(rq) слабо меняется от r в пределах от r = 3 до ρ = ∞ то данный расчет справедлив и для полидисперсных взвесей с практически любым распределением частиц по размерам. В этом случае определяется средний эффективный диаметр частиц.
Кроме принципиального ограничения на минимальный размер частиц во взвеси ρmin= 3 при котором минимально измеряемый диаметр частиц составляет dmin λ /n, есть еще приборное ограничение, определяемое современным уровнем оптического приборостроения, на максимально возможный размер частиц, который можно измерить данным способом. Как говорилось выше, обычно минимальный угол q, от которого начинаются измерения, составляет 30-40 мин, но есть приборы, позволяющие измерять от q 5 мин. Если взять этот угол, то из равенства (1) rmax 1200 и из уравнения (3) dmax 400 λ /n.
На фиг. 1 изображен график зависимости доли светового потока, рассеянного в конус с углом раствора равным апертурному углу q от произведения дифракционного параметра r на апертурный угол q При изменении rq от 0 до 3 f(rq) изменяется от 0 до 0,9. График представляет S-образную кривую с максимумом первой производной при f(rq) 0,5 и rq 1,8.
На фиг.2 приведены зависимости доли светового потока, рассеянного в апертурный угол q, от величины этого угла для различных дифракционных параметров r. Цифры у кривых соответствуют: 1 r 40; 2 r 15,2; 3 r 3,8 4 r 3, при этом 1 и 4 теоретически рассчитанные кривые, а 2 и 3 получены экспериментально для частиц латекса двух размеров.
Примеры.
Проведены измерения на водных суспензиях стандартизованных по размерам частиц латекса двух классов М050 и М150. Измерения выполнены на спектрофотометре с дополнительным оптико-механическим блоком, позволяющим в непрерывном автоматическом режиме регистрировать показатель ослабления F(q) светового потока при изменении расстояния от кюветы с образцом до входного окна интегрирующей сферы с приемником светового потока, что соответствует изменению апертурного угла приемника светового потока. При этом апертурный угол изменялся от 0,00087 до 0,5 рад. Длина волны излучения составляла 0,55 мкм. Показатель преломления воды для этой длины волны равен n 1,33. По данным измерения рассчитаны доли светового потока, рассеянного в апертурном углеq по формуле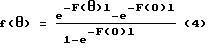
где l длина кюветы, м.
1. Частицы латекса класса М050, диапазон размеров частиц от 0,45 до 0,55 мкм. На фиг.2 расчеты по формуле (4) представлены кривой 3. По этой кривой для доли света, рассеянного в апертурном угле θ, равной половине всего рассеянного светового потока, при которой размер частиц определяется наиболее точно, находим q 0,46 рад и тогда диаметр частиц по формуле (3) равен d 0,57•0,55/(1,33•0,46)=0,51 мкм.
2. Частицы латекса класса М150, диапазон размеров частиц от 1,25 до 1,75 мкм. На фиг. 2 расчеты по формуле (4) представлены кривой 2. Для f(q) 0,5 находим q 0,15 и диаметр частиц равен d 0,57•0,55/(1,33•0,15) 1,57 мкм.
Использование предлагаемого способа позволит уменьшить трудоемкость определения размеров частиц за счет исключения громоздких теоретических расчетов отношения F(q)/F(0) для частиц разных размеров (причем, если неизвестен хотя бы порядок величины размера исследуемых частиц, то необходим расчет для возможно более полного ряда размеров) и исключения предварительного измерения показателя преломления вещества исследуемых частиц.
Кроме того, данный способ позволяет определять средний эффективный (в оптическом отношении) размер частиц полидисперсных суспензий. Последнее может быть использовано для контроля технологических процессов измельчения каких-либо веществ на предприятиях, где требуется размол веществ до определенной степени дисперсности.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРОВЕДЕНИЯ АНАЛИЗОВ КРОВИ И АНАЛИЗАТОР КРОВИ | 2007 |
|
RU2347224C2 |
| ЛАЗЕРНЫЙ АНАЛИЗАТОР МИКРОЧАСТИЦ И БИОЛОГИЧЕСКИХ МИКРООБЪЕКТОВ | 2000 |
|
RU2186362C1 |
| Способ определения параметров функции распределения частиц по размерам | 1988 |
|
SU1548713A1 |
| Способ определения вероятности выживания кванта в дисперсных средах | 1987 |
|
SU1476355A1 |
| СПОСОБ РАЗДЕЛЬНОГО ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ПОГЛОЩЕНИЯ И РАССЕЯНИЯ ФОТОНОВ НА ЕДИНИЦУ ПУТИ В ТВЕРДЫХ ОПТИЧЕСКИХ МАТЕРИАЛАХ | 2013 |
|
RU2533538C1 |
| Способ мониторинга атмосферных примесей | 1990 |
|
SU1800325A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ЖИРА И БЕЛКА В МОЛОКЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1993 |
|
RU2061237C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ СПЕКТРАЛЬНОГО ПОГЛОЩЕНИЯ СВЕТА МОРСКОЙ ВОДОЙ | 2024 |
|
RU2838142C1 |
| АКУСТООПТИЧЕСКИЙ ПЕРЕСТРАИВАЕМЫЙ ФИЛЬТР | 2000 |
|
RU2182347C2 |
| Способ определения содержания жира и белка в молоке | 1986 |
|
SU1441308A1 |
Использование: изобретение относится к физическим способам анализа, применяемым в гидрооптике, гидробиологии, биотехнологии, и предназначено для определения размеров частиц в суспензии. Сущность изобретения: измеряется зависимость показателя F(θ) ослабления (или рассеяния) света от величины апертурного угла θ приемника светового потока для анализируемой суспензии, по ней определяется апертурный угол θ, при котором доля светового потока, рассеянного в этом апертурном угле, равна половине всего рассеянного света. Диаметр d частиц в суспензии определяется по формуле d = 0,57λ/nθ , где λ - длина волны излучения, n - показатель преломления дисперсионной среды суспензии. 2 ил.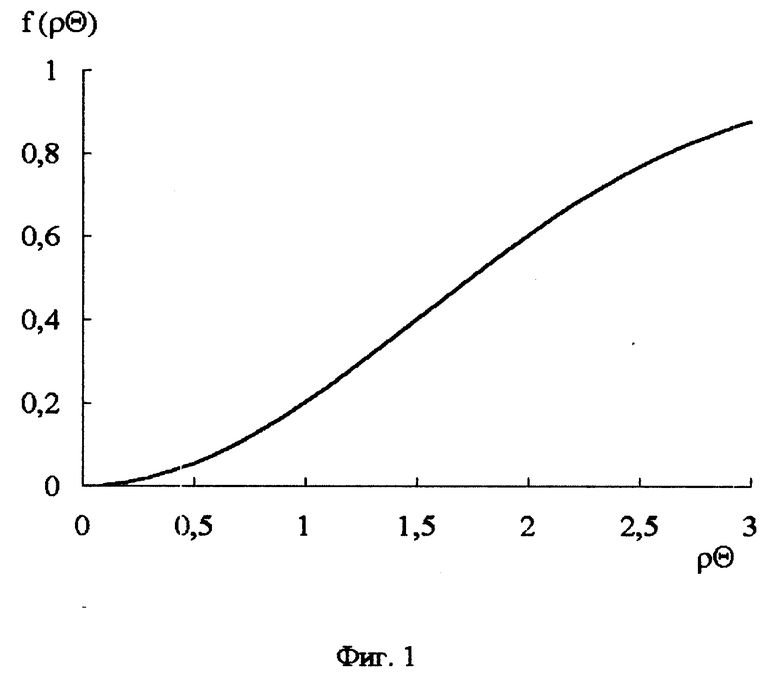
Оптический способ определения размера частиц в суспензии на основе измерения ослабления светового потока, отличающийся тем, что регистрируют зависимость показателя ослабления светового потока от величины апертурного угла θ приемника светового потока, по ней определяют апертурный угол q, при котором световой поток, рассеянный в конусе с апертурным углом θ, составляет половину всего рассеянного светового потока, а диаметр α частиц в суспензии определяют по формуле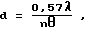
где l - длина волны излучения;
n показатель преломления дисперсионной среды суспензии.
| Кленин В.И | |||
| и др | |||
| Характеристические функции светорассеяния дисперсных систем | |||
| - Изд-во Саратовского университета, 1977, с | |||
| Способ гальванического снятия позолоты с серебряных изделий без заметного изменения их формы | 1923 |
|
SU12A1 |
| Latimer P.et al.Journal of Colloid Interface Science, 1985, v 105, N 2, р.410 - 416 | |||
| Latimer p.N | |||
| IEEE, 1984, Y QE-20, N 12 | |||
| Реверсирующий механизм при джигерсах | 1922 |
|
SU1529A1 |
Авторы
Даты
1997-12-10—Публикация
1994-10-11—Подача