Изобретение относится к области измерения оптических характеристик твердых материалов, определяющих световые потери в них, связанные как с поглощением, так и с рассеянием фотонов.
Основным недостатком известных способов измерения поглощающих и рассеивающих характеристик оптических сред является невозможность с их помощью правильно разделить вклады поглощения и рассеяния в общее ослабление светового потока, обусловленная некорректностью моделей процессов распространения света, используемых при расчетах. При этом сами понятия - показатель рассеяния, коэффициент рассеяния, применяющиеся при оценках интенсивности рассеяния, не соответствуют истиной физической картине данного процесса.
В заявляемом изобретении вводится и обосновывается новое понятие - величина вероятности рассеяния фотона на единицу пути, зависящая от угла рассеяния, позволяющее осуществлять правильную метрологию выпускаемых оптических материалов.
Только в идеальном случае абсолютно не рассеивающего вещества, никогда не реализуемом на практике, строго выполняется экспоненциальный закон ослабления света вследствие поглощения - закон Бугера-Ламберта [1]:

где I0 - интенсивность светового потока, вступающего в слой вещества толщиной h, I - интенсивность светового потока, выходящего из слоя, αа - показатель поглощения.
Так как образец вещества имеет входную и выходную границы, ортогональные лучу, как правило, плоские, гладкие и взаимно параллельные, учет многократных отражений от этих границ внутри образца приводит к известной формуле (формуле Хадсона), связывающей экспериментально измеряемый коэффициент пропускания света T с толщиной образца вдоль луча h и показателем поглощения α [2]

где R=(n-1)2/(n+1)2 - коэффициент отражения света при нормальном падении, n - показатель преломления вещества.
В случаях, когда в веществе наблюдаются заметное рассеяние света, соизмеримое с поглощением, использование указанных формул приводит к грубым погрешностям, обусловленным невыполнением закона Бугера-Ламберта. В частности, рассчитанные согласно этим формулам показатели поглощения αa1 и αa2 у двух образцов с измеренными коэффициентами пропускания T1 и T2 и толщинами h1 и h2, вырезанных из исходного образца толщиной h (h=h1+h2), у которого также измерялся коэффициент пропускания T, оказываются у обоих образцов меньше, чем у исходного: αa1<αa2; αa2<αa [3]. Между тем, если исходный образец однороден по поглощающим и рассеивающим свойствам, то все три величины должны быть одинаковыми: αa1=αa2=α, а если неоднороден, то одна из величин - αa1 или αa2 - должна быть больше, а другая меньше, чем величина αa у исходного длинного образца.
Невыполнение экспоненциального закона ослабления света при наличии рассеяния обусловлено тем, что часть однократно рассеянных фотонов может поглощаться внутри образца, но другая часть фотонов в результате последующих актов рассеяния и (или) отражения от боковых поверхностей образца может вновь двигаться в исходном направлении и вносить вклад в общий световой поток, выходящий из образца и фиксируемый фотоприемником. При этом не выполняется и более точное соотношение, в которое входит показатель экстинкции (ослабления) света α, являющийся суммой показателей поглощения αa и рассеяния αs [4]:
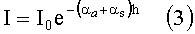
По сравнению с таким модифицированным законом Бугера-Ламберта процесс прохождения излучения через поглощающую и рассеивающую среду значительно точнее описывается нестандартным уравнением переноса (УПИ) [5-7], в которое входит такая важная характеристика, как индикатриса рассеяния - зависимость интенсивности рассеяния света элементарным объемом вещества от угла рассеяния I(Θ). Однако интегрально-дифференциальное уравнение переноса в общем случае не имеет аналитического решения и на практике используют те или иные его упрощения, например двухпотоковую модель, диффузионное приближение, осевую модель и т.д. Недостатком указанных моделей является применение не имеющего вследствие невыполнения закона Бугера-Ламберта физического обоснования таких понятий и величин, как показатели рассеяния и экстинкции. В частности, в рамках так называемой осевой модели получена формула для оценки относительной доли баллистических фотонов (фотонов, идущих в исходном осевом направлении) в общем излучении, прошедшем сквозь рассеивающую среду [8]:
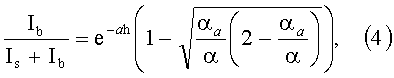
где Ib - интенсивность баллистических фотонов, Is - интенсивность рассеянных фотонов, α - показатель экстинкции, αа - показатель поглощения, h - толщина образца вдоль луча.
Выражение (1) выведено без учета индикатрисы рассеяния, без учета актов многократного рассеяний фотонов внутри образца и отражения фотонов от его границ. Если измерить коэффициенты пропускания света T1 и T2 образцами из одного и того же исследуемого вещества, но с различными толщинами h1 и h2, то, в пределах справедливости формулы (4), можно получить значения показателя поглощения αа и показателя рассеяния αs путем решения системы уравнений (2), вытекающей из (4) [8]:

Известен способ определения оптических характеристик рассеивающей среды, основанный на измерении сдвига фазы прошедшего через образец модулированного лазерного излучения с различными (как минимум двумя) частотами модуляции и определении коэффициента поглощения и редуцированного коэффициента рассеяния по результатам измерений на базе диффузионного приближения уравнения переноса излучения [8]. Недостатками способа являются необходимость применения сложного оборудования, в частности источника модулированного лазерного излучения с изменяемой частотой модуляции, а также использование при расчетах диффузионного приближения, дающего грубые погрешности вследствие упрощенной модели процесса распространения излучения в поглощающем и одновременно рассеивающем веществе.
Известен способ определения потерь света, связанных с рассеянием, с помощью фотометрического шара [9], применяемый в ГОИ им. С.В. Вавилова. Недостатком способа является невозможность получения с его помощью данных о распределении рассеянного света по углам, т.е. об индикатрисе рассеяния, поскольку измеряется только общий рассеянный световой поток, вышедший из кристалла.
Известны также способ определения индикатрисы рассеяния света в кристаллах с помощью измерения функции рассеяния линии (ФРЛ), описанных в [10], а также способ, основанный на измерении угловой зависимости интенсивности рассеяния лазерного света, апробированный на кристаллах германия и кремния [11]. Недостатком указанных способов является то, что угловое распределение рассеянного света, вышедшего из образца, в общем случае не совпадает с угловым распределением света, рассеянного элементарным объемом вещества внутри образца.
Известен способ фотометрии рассеивающих сред и реализующий его фотометрический модуль [12], основанный на измерении двух коэффициентов пропускания света образцами из одного вещества с различными толщинами вдоль луча и последующем решении системы уравнений (5), взятый в качестве прототип для предлагаемого изобретения.
Недостатком прототипа, как и других известных аналогичных способов, является неточность физической модели процесса распространения света и основанной на ней системы уравнений, из которых вычисляются показатели поглощения и рассеяния света в исследуемой среде.
Действительно, из любого из уравнений (5) следует, что в абсолютно нерассеивающей среде (αs=0) коэффициент пропускания света T будет равен

т.е. световой поток должен строго подчиняться экспоненциальному закону Бугера-Ламберта. Однако учет многократного отражения от входной и выходной границ образца дает другое - правильное выражение для коэффициента пропускания в виде

где R - коэффициент отражения, зависящий от показателя преломления вещества n.
Также из любого из уравнений (5) следует, что в абсолютно непоглощающей среде (αa→0) измеряемый коэффициент пропускания света T будет равен

T=1/(1+αsh).
Этот результат означает, что при достаточно малых значениях произведения показателя рассеяния на толщину образца (αsh) коэффициент пропускания света образцом может быть сколь угодно близким к единице. Между тем коэффициент пропускания света веществом с показателем преломления n не может иметь значение, больше чем

где R - коэффициент отражения. Например, для воды (n=1,33) имеем T<0,98; для стекла (n=1,5) T<0,96; для кристаллов парателлурита (n=2,5) Т<0,82, для кристаллов германия (n=4 в ИК диапазоне) T<0,64. На самом деле вследствие многократного отражения внутри образца величина T еще меньше.
Таким образом, даже в предельных случаях чисто поглощающего или чисто рассеивающего вещества система уравнений (5), основанная на приближенной осевой модели и используемая при расчетах в способе, взятом за прототип, дает физически некорректные результаты и не отражает истинного характера зависимости между свойствами вещества и коэффициентами пропускания света изготовленных из него образцов.
Неправильное определение рассеивающих и поглощающих характеристик оптических материалов возможное при использовании известных способов - как аналогов, так и прототипа - может приводить к грубым ошибкам при сертификации и выборе материала для оптических устройств. Два образца одинаковых размеров из различных кристаллов одного и того же вещества, у которых оказались равными коэффициенты пропускания света, с точки зрения известных способов будут считаться одинаковыми по рассеивающим и поглощающим свойствам. Однако при равных коэффициентах пропускания в одном образце может быть выше вероятность поглощения, но ниже вероятность рассеяния фотонов по сравнению с другим образцом. Тогда в первом образце будут меньшими оптические искажения изображений и его можно использовать в качестве линз объективов, но он будет нагреваться сильнее и, возможно, разрушаться (лазерный пробой) при использовании в качестве элемента проходной оптики для мощных лазеров. Второй образец будет давать большие оптические искажения и его не следует использовать, например, в тепловизионных устройствах, но зато его можно использовать в устройствах, связанных с мощными лазерными пучками.
Целью предлагаемого изобретения является повышение точности раздельного определения истинных значений характеристик интенсивностей поглощения и рассеяния света у твердых веществ в диапазонах их прозрачности, используемых в качестве элементов оптических, оптоэлектронных и лазерных устройств.
Заявляемое изобретение иллюстрируется фиг.1÷9.
Фиг.1 - Разбиение образца на N слоев толщиной d, в каждом из которых вероятность поглощения фотона равна р.
Фиг.2 - Система координат для цилиндрического образца, используемая при моделировании траектории фотонов.
Фиг.3 - Возможные варианты траекторий фотонов в поглощающем и рассеивающем веществе.
Фиг.4 - Определение истинных значений вероятностей поглощения 



Фиг.5 - Отполированный шарик диаметром 8 мм, изготовленный из кристалла парателлурита и предназначенный для измерения индикатрисы рассеяния света.
Фиг.6 - Зависимости вероятностей рассеяния ps от вероятностей поглощения pa фотонов на 1 см, дающего экспериментально измеренные коэффициенты пропускания света с длиной волны 535 нм двумя образцами с различной толщиной, вырезанными из одного кристалла парателлурита.
Фиг.7 - Монокристалл германия, использованный при определении вероятностей поглощения и рассеяния фотонов.
Фиг.8 - Вид индикатрисы рассеяния света с длиной волны 10,6 мкм кристаллом германия.
Фиг.9 - Зависимости вероятностей рассеяния ps от вероятностей поглощения pa фотонов на 1 см, дающие экспериментально измеренные коэффициенты пропускания света с диной волны 10,6 мкм двумя образцами с различной толщиной, вырезанными из одного кристалла германия.
Сущность изобретения
Способ включает последовательное измерение коэффициентов пропускания света T1 и T2 двумя образцами с взаимно параллельными, отполированными торцами, изготовленными из одного и того же материала, но имеющими различные толщины h1 и h2 вдоль оси луча. Это могут быть, например, исходный образец и отрезанная от него часть с вновь отполированным торцом со стороны среза.
Далее, в отличие от известных способов и в том числе прототипа, производится компьютерный расчет поглощающих и рассеивающих характеристик материала с помощью математического моделирования процесса распространения изначально параллельного пучка света в образце с плоскопараллельными торцами, ортогональными оси пучка.
При этом используется следующая объемная модель взаимодействия пучка фотонов с веществом внутри образца и на его поверхностях.
Внутри образца ослабление светового потока, связанное с поглощением, подчинятся закону Бугера-Ламберта согласно формуле (1). Образец толщиной h условно разбивается вдоль оси пучка на N слоев толщиной d каждый.
В качестве исходного параметра задается величина p - вероятность поглощения фотона внутри слоя. Таким образом, вероятность того, что фотон преодолеет один слой без поглощения, равен (1-p), а вероятность того, что фотон преодолеет весь образец, равен (1-p)N, Фиг.1.
Поскольку, согласно (1), прошедший расстояние h=Nd световой поток должен быть ослаблен из-за поглощения в 

откуда вытекает связь между параметрами, характеризующими поглощение:

Так как величина р зависит от выбора толщины элементарного слоя d, удобно ввести такой параметр, как вероятность pa поглощения фотона на пути в 1 см:

Таким образом, обе величины αa и pa полностью характеризуют поглощающую способность вещества.
Ослабление светового потока из-за рассеяния не подчиняется экспоненциальному закону Бугера-Ламберта, поэтому при моделировании введение в рассмотрение показателя αs, аналогичного по физическому смыслу показателю поглощения αa, является некорректным упрощением и следует использовать только величину ps(Θ) - вероятность того, что фотон в слое толщиной d будет рассеян в направлении, составляющем угол Θ с направлением, вдоль которого фотон входил в слой. Функция p(Θ) является индикатрисой рассеяния и экспериментально определяется при реализации предлагаемого способа.
Для численного моделирования должны быть также известны или измерены:
h1 - толщина первого образца вдоль луча;
h2 - толщина второго образца вдоль луча;
D - диаметр образца (в случае образца цилиндрической формы);
l×m - размеры образца в поперечных оси направлениях (в случае образца с прямоугольным сечение);
Dф - диаметр входного окна фотоприемника;
S - расстояние между выходным торцом образца и входным окном фотоприемника;
n - показатель преломления вещества для длины волны λ используемого при измерениях излучения.
В совокупности с измеренными значениями коэффициента пропускания света образцами T1 и T2 указанные величины достаточны для определения показателя поглощения света αa, вероятности поглощения фотона pa на 1 см пути в веществе и ps(Θ) - вероятности рассеяния фотона под углом Θ к исходному направлению на 1 см пути в веществе.
Моделирование
Процесс прохождения излучения через образец моделируется как совокупность актов отражения, поглощения, рассеяния или свободного движения, происходящих с каждым из виртуальных фотонов, направляемых перпендикулярно входному торцу образца в виде равномерного по плотности потока интенсивностью I0. Интенсивность излучения на выходе из образца I измеряется суммой траекторий всех фотонов, пересекающих входное окно фотоприемника. Каждая такая траектория входит в сумму со своим косинусом угла, составляемого ею с осью образца. Торцы и боковая поверхность предполагаются идеально гладкими. Излучение предполагается неполяризованным, интерференционные эффекты не учитываются.
Геометрическая форма образца задается математически с помощью совокупности поверхностей, в случае образца цилиндрической формы - двух плоскостей и цилиндрической поверхности радиуса R=D/2, Фиг.2.

Образец длиной h разбивается на N элементарных слоев перпендикулярно оси.
Положение фотона в компьютерном эксперименте изменяется дискретно с шагом d=h/N и в каждый момент времени задается декартовыми координатами [xj, yj, zj). Также заполняется предыдущее положение фотонов (xj-1, yj-1, zj-1). Если при подстановке текущих и предыдущих координат фотона в одно из выражений (9) его значение изменяет знак, считается, что фотон пересек соответствующую поверхность. В этом случае вычисляются координаты точки пересечения и угол падения i1. Далее вычисляются вероятности каждого из возможных случаев - отражения фотона или преломления с выходом за пределы образца, и с учетом значений этих вероятностей случайным образом выбирается одно из событий. Вероятности отражения po считаются равными коэффициентам отражения r, которые вычисляются согласно формулам Френеля [1]:
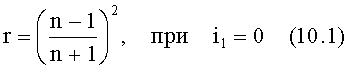


при 
Поскольку никаких событий, кроме отражения или преломления на границе образца происходить не может, вероятность преломления pn считается равной pn=1-po.
На пути длиной d=h/N вдоль любого направления внутри образца задаются вероятность поглощения фотона pa и вероятность рассеяния фотона ps так, чтобы выполнялось условие (pa+ps)<1. На каждом шаге фотон может испытать поглощение или рассеяние, если сгенерированное программой псевдослучайное число оказывается меньше заданных вероятностей поглощения или рассеяния.
На Фиг.3 показаны различные типы траекторий фотонов, получаемые в ходе компьютерного эксперимента.
Число используемых при моделировании фотонов Ф, достаточное для достижения требуемой точности вычисления параметров поглощения и рассеяния, должно составлять не менее 106-107 шт.
По результатам измерений коэффициентов пропускания света T1 и T2 обоими образцами вычисляются приближенные значения показателей поглощения αa1 и αa2 согласно формуле (2), в которой не учитывается расстояние.
Далее согласно формуле (8) вычисляются приближенные значения вероятностей поглощения pa:

Диапазоны значений pa от 0 (чистое рассеяние) до pa1 и pa2 (чистое поглощение) разбивается на М участков, и для каждой из образовавшихся точек: 0, pa1/М, 2pa1/М…pa1; 0, pa2/М, 2pa2/М…pa2 путем моделирования находятся такие М значения вероятностей рассеяния 
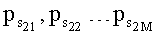
Результатом моделирования являются две зависимости 

Поскольку на самом деле образцы изготовлены из одного и того же материала, полученные зависимости должны иметь три общие точки - для чисто рассеивающего вещества (pa=0; ps≠0), для чисто поглощающего вещества (pa≠0; ps=0), а также еще одну точку, значения pa≠0 и ps≠0 в которой и являются истинными значениями 

Примеры применения способа согласно изобретению.
Пример 1. Определение вероятностей поглощения и рассеяния фотонов на единицу пути в крупногабаритном монокристалле парателлурита (α-ТеО2), выращенном способом Чохральского и имеющего диметр 66 мм и высоту 45 мм, для длин волны излучения 535 нм.
Из части кристалла вырезают и полируют по классу Р II шарик диаметром 8 мм с шестью попарно ортогональными площадками, Фиг.5, через которые вводился луч лазера с длиной волны излучения 535 нм. С помощью измерителя лазерной мощности определялась индикатриса рассеяния - зависимость интенсивности рассеяния от угла рассеяния Θ, которая соответствовала рэлеевской индикатрисе ps(Θ)=(1+cos2Θ).
Далее из кристалла вырезают и полируют по классу Р II цилиндрический образец диаметром D=60 мм и толщиной вдоль оси [110] h1=30 мм. После разрезания исходного образца и полировки толщины образовавшихся частей составляли h2=16 мм и h3=12 мм. У исходного и одного из меньших образцов измеряют коэффициенты пропускания Т1 и T2 света лазера с длиной волны излучения λ=535 нм по схеме, в которой фотоприемником служил измеритель лазерной мощности (Laser Power Meter. PHOTON Inc.).
Для расчета величин pa и ps методом моделирования траекторий фотонов используют следующие значения параметров:

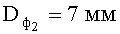
Результаты компьютерного расчета зависимостей ps(pa) представлены на Фиг.6. Искомые вероятности поглощения и рассеяния на пути 1 см в кристалле найдены по точке пересечения двух графиков и равны, соответственно, pa=0,003 и ps=0,012.
Пример 2. Определение вероятностей поглощения и рассеяния фотонов на единицу пути в кристалле германия для длины волны излучения 10,6 мкм.
В качестве исследуемого материала были использованы образцы, вырезанные из монокристалла германия, выращенного из расплава в направлении [111] способом Чохральского (Фиг.7) и имеющего диаметр 63 мм и высоту 330 мм.
Из кристалла был вырезан и отполирован по классу Р III цилиндрический образец диаметром D=64 мм с толщиной вдоль оси [111] h1=80 мм. Индикатриса рассеяния p(Θ) материала определялась для длины волны λ=10,6 мкм экспериментально методом ФРЛ (функции рассеяния линии) [10]. Она имела вид, представленный на Фиг.8, и соответствовала индикатрисе малоуглового рассеяния Ми с несколькими максимумами и минимумами.
При компьютерных расчетах индикатриса была аппроксимирована наиболее точно полиномами Лежандра согласно выражению:
p(Θ)=0,565+0,224cos(Θ)+0,425(cosΘ)2-4,191(cosΘ)3+3,807(cosΘ)4+17,467(cosΘ)5-8,155(cosΘ)6-26,918(cos©)7+51252(cosΘ)8+13,951(cosΘ)8
Далее исходный образец разрезался, и после повторной полировки толщины образовавшихся частей составляли h2=38 мм и h3=11 мм. У исходного и после разрезания у одного из меньших образцов измерялись коэффициенты пропускания света T1 и T2 с помощью инфракрасного спектрофотометра ИКС-29. Для расчета величин pa и ps методом моделирования траекторий фотонов использовались следующие значения параметров:
Результаты компьютерного расчета зависимостей ps(pa) представлены на Фиг.9. Искомые вероятности поглощения и рассеяния на пути 1 см в кристалле найдены по точке пересечений двух графиков и равны, соответственно, pa=0,0045 и ps=0,0085.
Изобретение может найти применение в метрологии оптического качества выпускаемых стекол, поликристаллов и монокристаллов, используемых во всех участках оптического диапазона - от жесткого УФ излучения (200-250 нм) и до среднего ИК-диапазона (20-25 мкм). Область использования изобретения включает в себя производство оптических материалов и устройств оптики, оптоэлектроники и фотоники.
Источники информации
1. Ландсберг Г.С. Оптика. М.: Физматлит. . 848 с.
2. Уханов Ю.И. Оптические свойства полупроводников. М.: Наука. 1977. 368 с.
3. Каплунов И.А. Зависимость коэффициентов пропускания света кристаллами от их толщины // Оптический журнал. 2005. T.72. №12, с.59-65
4. Физическая энциклопедия в 65-и томах. М.: Советская энциклопедия. Под. ред. A.M. Прохорова. 1988.
5. Кольчужин A.M., Учайкин В.В. Введение в теорию прохождения частиц через вещество. М.: Атомиздат. 1978.
6. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. М.: Мир. T.1. 1981.
7. Кейз К., Цвайфель П. Линейная теория переноса. М.: Физматлит. 2004.
8. Y. Tsuchiya. Apparatus for measuring optical information in scattering medium and method therefore. Patent US 5477051. Dec. 19. 1995.
9. Шайович С.Л., Каплунов И.А., Колесников А.И. Контроль рассеяния инфракрасного излучения в германии методом фотометрического шара. // Заводская лаборатория. Диагностика материалов. 2005. Т.71. №9. С.47-50.
10.Kaplunov S.A., Kolesnikov A.I., Shaiovich S.L. Methods for Measuring Lights Scattering in Germanium and Paratellurite Crystals // Crystallography Reports. V.50 Suppl. 1. 2005. Р.546-552.
11.Воронков В.В., Воронкова Г.И., Зубов Б.В. и др. Рассеяние света, обусловленное микродеффектами в Si и Ge. // ФТТ. 1977. Т.19. Вып.6. С.1784-1791.
12. Данилов А.А., Маслобоев Ю.П., Селищев С.В., Терещенко С.А. Способ фотометрии рассеивающих сред и реализующий его фотометрический модуль. Патент РФ 2377540. 10.06.2008.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В КРОВИ | 2013 |
|
RU2536217C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ СВОЙСТВ НАНОЧАСТИЦ | 2014 |
|
RU2586938C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЧАСТИЦ, ВЗВЕШЕННЫХ В ЖИДКОСТИ, ПО СПЕКТРАМ МАЛОУГЛОВОГО РАССЕЯНИЯ СВЕТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2321840C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ И БИОФИЗИЧЕСКИХ ПАРАМЕТРОВ БИОТКАНИ | 2012 |
|
RU2510506C2 |
| СПОСОБ ФОТОДИНАМИЧЕСКОЙ ТЕРАПИИ ОНКОЛОГИЧЕСКИХ ЗАБОЛЕВАНИЙ | 2013 |
|
RU2539367C1 |
| СПОСОБ ФОТОМЕТРИИ РАССЕИВАЮЩИХ СРЕД И РЕАЛИЗУЮЩИЙ ЕГО ФОТОМЕТРИЧЕСКИЙ МОДУЛЬ | 2008 |
|
RU2377540C1 |
| Способ определения коэффициента поглощения и коэффициента диффузии излучения в твердых слабопоглощающих сильнорассеивающих материалах | 1988 |
|
SU1567936A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В БИОЛОГИЧЕСКИХ ТКАНЯХ | 2013 |
|
RU2517155C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАЗМЕРОВ ЧАСТИЦ | 1992 |
|
RU2035036C1 |
| СПОСОБ КВАНТОВОЙ КРИПТОГРАФИИ С ИСПОЛЬЗОВАНИЕМ ПАССИВНЫХ ОТРАЖАЮЩИХ И ПЕРЕНАПРАВЛЯЮЩИХ ЭЛЕМЕНТОВ, РАСПОЛАГАЕМЫХ НА КОСМИЧЕСКИХ АППАРАТАХ | 2014 |
|
RU2566664C1 |









Изобретение относится к области измерения оптических характеристик материалов, определяющих световые потери в них, связанные как с поглощением, так и рассеянием. Способ состоит в том, что измерения коэффициента пропускания света производят для двух образцов с различной толщиной, изготовленных из одного и того же исследуемого материала. Измеренные значения коэффициентов пропускания, данные о толщинах и диаметрах образцов, значение показателя преломления и определенная экспериментально индикатриса рассеяния (зависимость интенсивности рассеяния от угла рассеяния) используются для расчета вероятностей поглощения и рассеяния фотонов на единицу пути с помощью математического моделирования. При моделировании для обоих образцов находятся зависимости вероятностей рассеяния фотонов от вероятностей поглощения, которые дают измеренные экспериментально коэффициенты пропускания. Поскольку оба образца с разными толщинами вдоль луча изготовлены из одного и того же материала, обе модельные зависимости должны пересекаться в точке, в которой обе вероятности не равны нулю, а значения вероятностей в этой точке должны являться истинными вероятностями поглощения и рассеяния фотонов на единицу пути в исследуемом материале, одинаковыми для обоих образцов. Изобретение позволяет с максимально возможной точностью определять вероятности поглощения и рассеяния фотонов, что позволяет правильно производить классификацию и сертификацию партий материалов, а также подбор материала с необходимыми поглощающими и рассеивающими свойствами с целью повышения воспроизводимости характеристик соответствующих оптических, оптоэлектронных и лазерных устройств. 9 ил.
Способ раздельного определения вероятностей поглощения и рассеяния фотонов на единицу пути в твердых оптических материалах, включающий облучение материала источником направленного излучения, измерение индикатрисы рассеяния света материалом, поочередное измерение коэффициентов пропускания света двух образцов материала различной толщины, отличающийся тем, что на основе ранее произведенных инструментальных измерений для каждой толщины образца дополнительно проводят компьютерное моделирование траекторий фотонов в материале с построением зависимостей вероятностей рассеяния от вероятностей поглощения, причем из общей точки этих зависимостей проводят горизонталь и вертикаль до пересечения с осями координат с получением искомых величин.
| СПОСОБ ФОТОМЕТРИИ РАССЕИВАЮЩИХ СРЕД И РЕАЛИЗУЮЩИЙ ЕГО ФОТОМЕТРИЧЕСКИЙ МОДУЛЬ | 2008 |
|
RU2377540C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ОБЪЕМНОГО РАССЕЯНИЯ И ПОГЛОЩЕНИЯ В ОПТИЧЕСКИХ МАТЕРИАЛАХ | 1991 |
|
RU2035037C1 |
| Способ определения коэффициента поглощения и коэффициента диффузии излучения в твердых слабопоглощающих сильнорассеивающих материалах | 1988 |
|
SU1567936A1 |
| ФОТОМЕТР | 2008 |
|
RU2371703C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК ОДНОРОДНОГО РАССЕИВАЮЩЕГО ВЕЩЕСТВА | 2009 |
|
RU2413930C1 |
| Устройство для отсоса загрязненного воздуха | 1973 |
|
SU580414A1 |
| US 6335792 B1, 01.01.2002 | |||
| EP 0627619 A1, 07.12.1994. | |||
Авторы
Даты
2014-11-20—Публикация
2013-08-19—Подача