Изобретение относится к области машиностроения и может быть использовано для замены прямозубых цилиндрических передач в условиях повышенных требований к долговечности и габаритам подшипниковых узлов и снижению вибрации и соответствующего им шума в осевом направлении.
Известна зубчатая передача, содержащая зацепляющиеся между собой косозубые цилиндрические колеса, у которой рекомендуемый угол наклона зубьев на делительных цилиндрах β≥7o [1] Считается, что выполнять косозубые цилиндрические передачи с углами менее указанных не следует, т.к. утрачиваются преимущества косозубых передач перед прямозубыми [2]
Недостатком указанных передач является возникновение осевой силы Fa, величина которой, без учета сил трения, равна
Fa = Ft•tgβ,
где Ft окружная сила в зацеплении.
Осевая сила дополнительно нагружает подшипники, снижая их долговечность и повышая габариты.
Известна также зубчатая передача, состоящая из цилиндрических косозубых колес, зубья которых имеют угол наклона на делительных цилиндрах, выбираемый в интервале 15' 1,5o [3]
Недостатком известной передачи является отсутствие конкретных рекомендаций для выбора оптимального угла наклона зуба на делительных цилиндрах для обеспечения минимальной величины осевой силы, нагружающей подшипники. Более того, возможен выбор такого угла наклона зубьев, который приводит к увеличению осевой силы и увеличению переменной составляющей осевой силы, вызывающей вибрации в осевом направлении.
Целью настоящего изобретения является повышение долговечности, снижение габаритов и массы подшипниковых узлов за счет уменьшения величины осевой силы и снижение вибраций в осевом направлении зубчатых колес и сопутствующего шума.
Поставленная цель достигается тем, что у косозубой цилиндрической передачи, содержащей зацепляющиеся между собой ведущее и ведомое колеса, угол наклона зубьев на делительных цилиндрах в интервале
0,1° ≤ β ≤ 3,5°
выбирается так, чтобы удовлетворялись условия: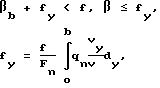
где f коэффициент трения скольжения между зубьями;
fy приведенная величина коэффициента трения скольжения зубьев вдоль мгновенной оси вращения-скольжения;
qn закон распределения нормальной силы по длине контактной линии;
Fn нормальная сила между контактирующими зубьями;
βb угол наклона зубьев на основных цилиндрах;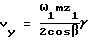 линейная скорость скольжения зубьев в направлении мгновенной оси вращения-скольжения (с достаточной для практических целей точностью);
линейная скорость скольжения зубьев в направлении мгновенной оси вращения-скольжения (с достаточной для практических целей точностью);
m нормальный модуль зацепления на начальных цилиндрах;
Z1 число зубьев ведущего зубчатого колеса;
V суммарная линейная скорость относительного скольжения зубьев в точках контакта: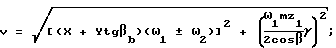
X абсциссы точек линии контакта в выбранной системе координат;
Y ординаты точек линии контакта;
ω1 и ω2 угловые скорости соответственно ведущего и ведомого зубчатых колес;
γ суммарный угол перекоса осей зубчатых колес в плоскости, перпендикулярной межосевому расстоянию.
Знак (+) для внешнего зацепления; знак (-) для внутреннего зацепления.
На фиг.1 изображена косозубая цилиндрическая передача в торцевой плоскости колес с выбранным положением осей координат XYZ с полюсом P, лежащим в торцевой плоскости.
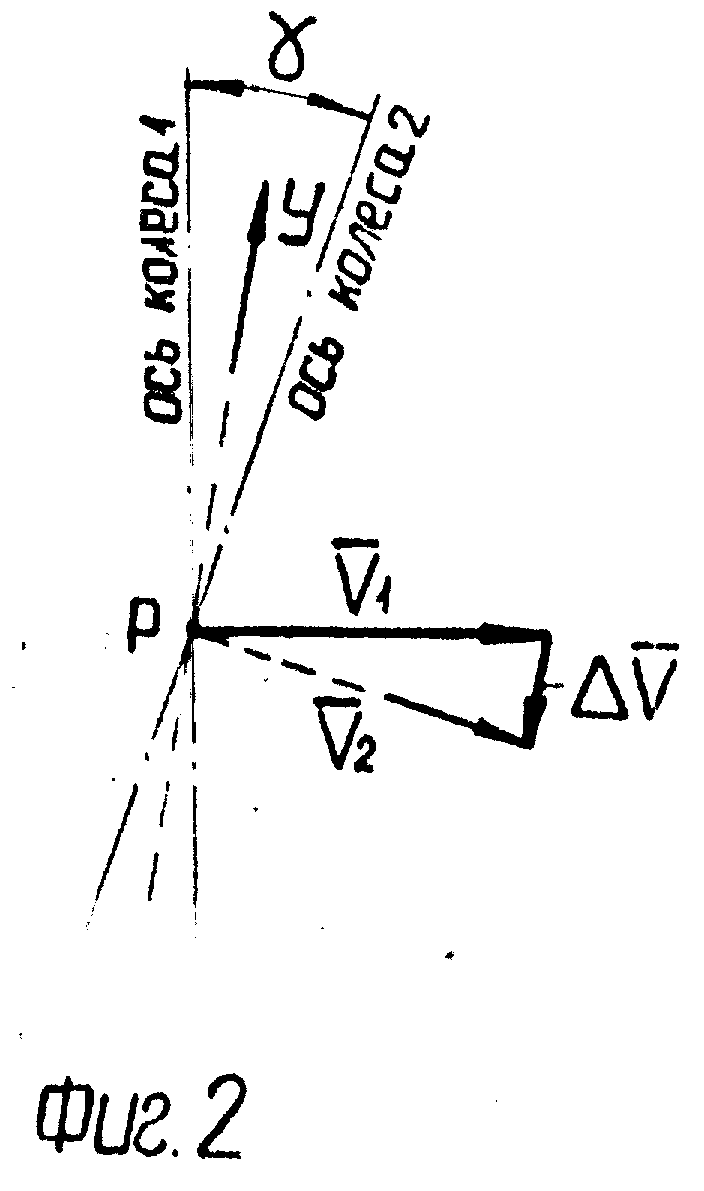
На фиг.2 изображен вид А зацепления колес фиг.1 с положение зубчатых колес в условиях перекоса из осей в плоскости, перпендикулярной межосевому расстоянию с указанием векторов линейных скоростей начальных окружностей.
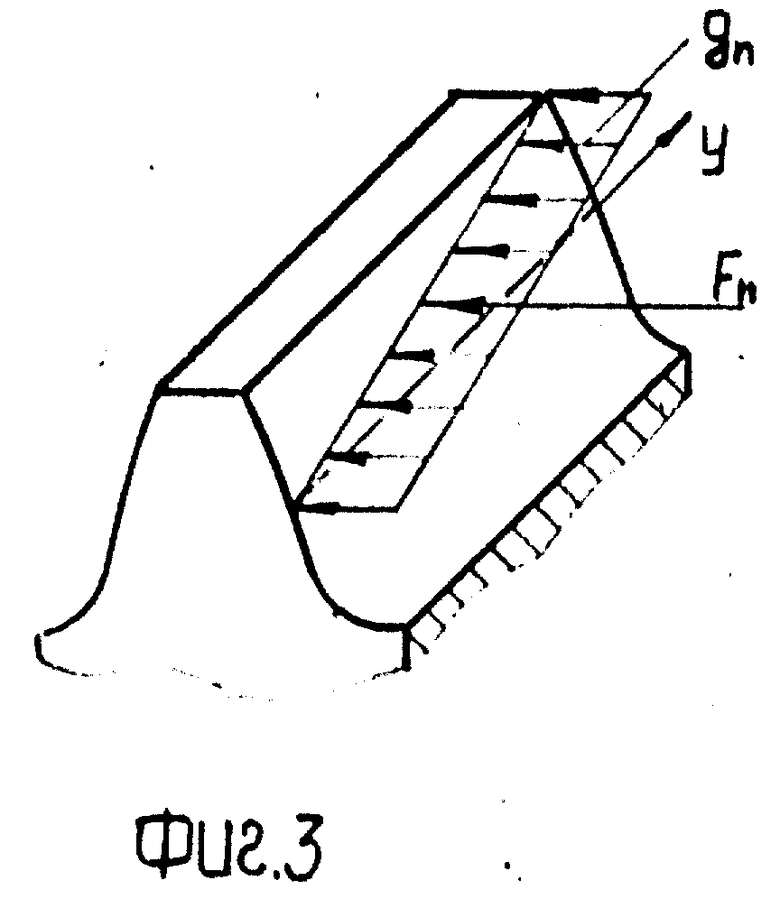
На фиг. 3 изображен частный случай нагружения косого зуба равномерно распределенной по контактной линии нагрузкой qn=const с указанием ее равнодействующей Fn, лежащей в плоскости зацепления.
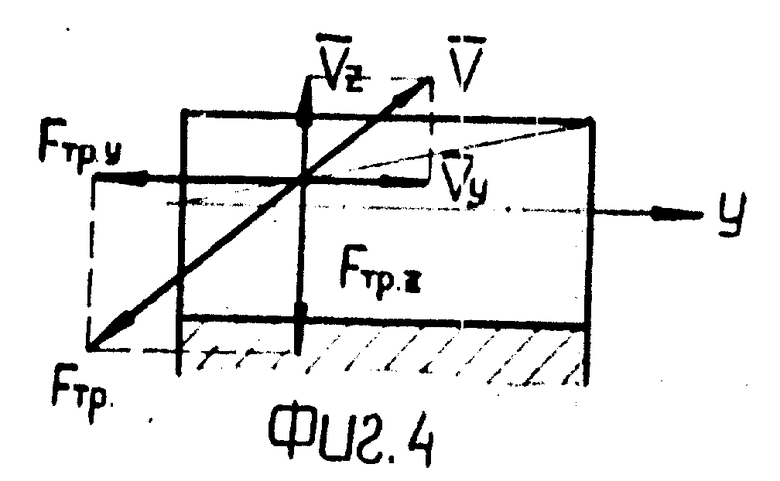
На фиг.4 показаны положения векторов скоростей относительного скольжения зубьев в произвольной точке контакта:
Vz направленный касательно к профилю зуба и Vy - направленный вдоль оси мгновенного вращения-скольжения Y в сечении Б-Б фиг.1, и положение векторов сил трения скольжения, направленных против векторов скоростей скольжения при равнодействующей Fn=1. Тогда силы трения
Fтр.у=Fn•fy=fy; Fтр.z=Fn•fz=fz,
полная сила трения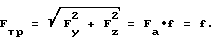
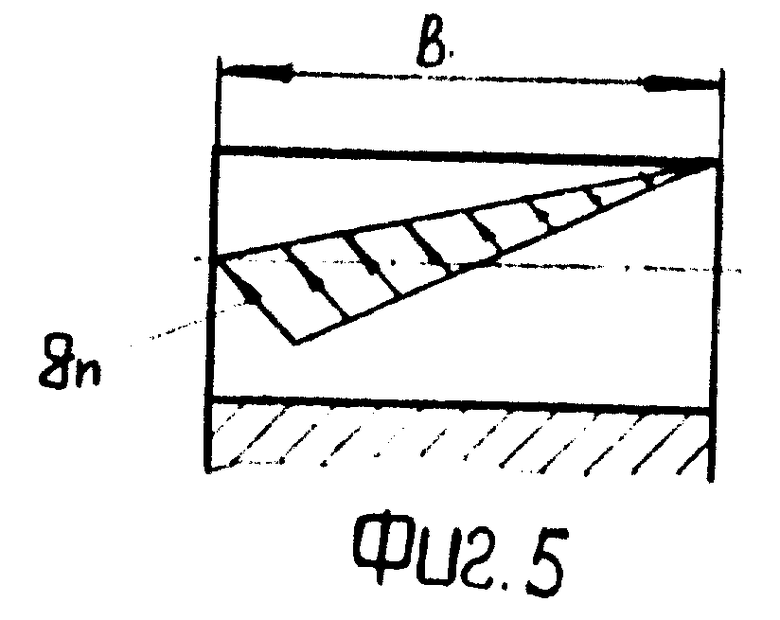
На фиг. 5 изображен частичный случай нагружения косого зуба при наличии концентрации нагрузки по длине контактной линии.
Исходя из подобия треугольников скоростей относительного скольжения и сил трения скольжения (фиг.4), можем записать: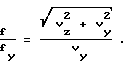
Из последнего выражения следует, что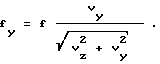
Косозубая цилиндрическая передача состоит из двух зацепляющихся колес: 1 ведущее зубчатое колесо, 2 ведомое (фиг.1).
Если ω1 угловая скорость ведущего колеса, а ω2 угловая скорость ведомого колеса, то при наличии в реальной передаче перекоса осей зубчатых колес зубья обязательно проскальзывают в направлении оси мгновенного вращения-скольжения (в нашем случае ось Y-ов) с линейной скоростью Vy (фиг.2). С достаточной для практических целей точностью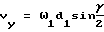
(при 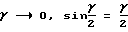 ).
).
(См. кн. Артоболевский И.И. Теория механизмов и машин. М. Наука, 1988, с. 486),
где d1 диаметр начального цилиндра колеса 1.
В то же время точки боковых поверхностей зубьев проскальзывают в поперечном направлении со скоростью (фиг.3)
v = X(ω1± ω2)
(знак "плюс" для внешнего зацепления, знак "минус" для внутреннего зацепления колес)
(См. кн. Артоболевский И.И. Теория механизмов и машин. М. Наука, 1988, с.444),
где X абсцисса точки контакта зубьев относительно начала координат - полюса зацепления.
Для зацепления косозубых колес абсцисса каждой точки контактной линии имеет величину
X = Xt+ Y•tgβb,
где βb угол наклона зубьев на основных цилиндрах;
X абсцисса точки контактной линии, расположенной в торцевой плоскости передачи.
Тогда vz = (Xt+ Ytgβb)(ω1± ω2).
Суммарная скорость скольжения для каждой точки (фиг.3)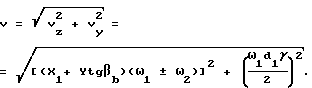
Используя положение, что скорости проскальзывания пропорциональны силам трения, получаем для каждой точки контактной линии косозубых колес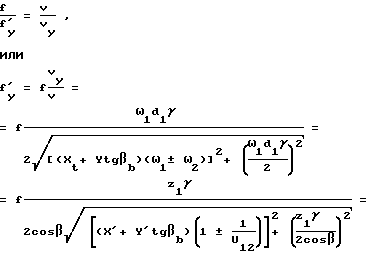
где X'= Xt/m; Y'= Y/m координаты точек контакта в выбранной системе в долях нормального модуля на начальных цилиндрах;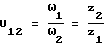 передаточное число передачи.
передаточное число передачи.
Из последнего выражения следует, что для прямозубой передачи, когда β = 0, βb = 0 при зацеплении в полюсе, т.е. X'=0, fy=f, т.е. у прямозубой цилиндрической передачи в условиях перекоса осей действует осевое усилие, максимальная величина которого возникает, когда контактная линия проходит через полюс зацепления, равное 
У косозубой цилиндрической передачи каждая точка линии контакта зубьев имеет свои координаты, значит, и свое значение 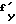 .
.
Расчетное значение для косозубой цилиндрической передачи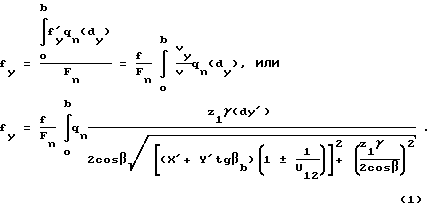
Тогда максимальная величина полного осевого усилия косозубой передаче с учетом сил трения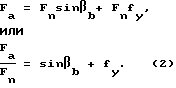
Принимая для малых углов sin βb = βb, а максимальное значение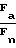 принимаем равным f для прямозубой передачи, получаем:
принимаем равным f для прямозубой передачи, получаем:
f = βb + fy. (3)
Из выражения (3) следует, что возможна косозубая передача, у которой полное осевое усилие будет меньше, чем у прямозубой передачи, т.е.
βb + fy < f. (4)
Второе условие для косозубой цилиндрической передачи β>fy принимается из условия нераскрытия контактов в подшипниках.
Найдем минимальное значение левой части выражения (4) в интервале углов b 0,1' 3,5o.
Выбор крайнего значения интервала b ≥0,1o объясняется стремлением исключить те прямозубые цилиндрические передачи, которые из-за наличия погрешности направления зубьев подпадают под действие настоящего изобретения. Выбор крайнего значения интервала b≤3,5o объясняется стремлением существенно снизить максимальную величину переменной составляющей осевой силы (приблизительно в 2 раза) по сравнению с прототипом.
То, что выполнение такой передачи возможно, рассмотрим на конкретных численных примерах.
Пример 1. Определить оптимальный угол наклона зуба передачи с параметрами: Z2=Z1=17; a 20o угол исходного контура; at 20o угол зацепления; m 5 мм нормальный модуль; b 30 мм - ширина зубчатого венца; γ 0,001 угол перекоса осей; f 0,1 коэффициент трения скольжения стальных зубьев. Распределение нагрузки равномерное, qn const (фиг.3).
Расчетная часть
1. В целях упрощения все расчеты ведутся при измерении длины в долях нормального модуля на начальных цилиндрах. Тогда, например, ширина зубчатого венца b 30 мм 6m.
2. В целях упрощения расчетов условно принимается m 1.
3. В целях упрощения расчетов принимается Ft 1, тогда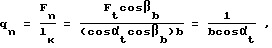
где lк = b/cosβb длина контактной линии;
αt угол зацепления в торцевой плоскости.
4. По формуле (1) с достаточной для практических целей точностью имеем: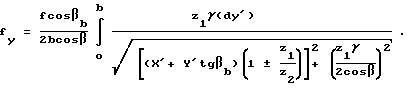
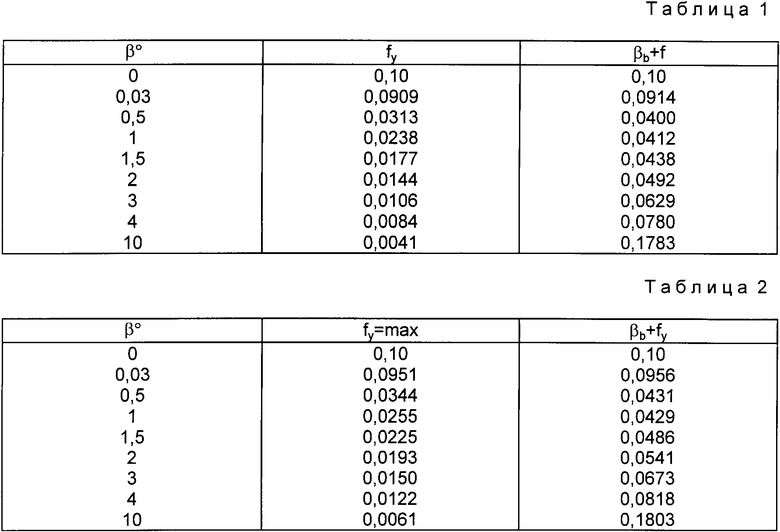
Значения fy fymax приведены в табл. 1 и взяты из распечаток значений fy в зависимости от угла β, полученных на ЭВМ для данного численного примера tgβb = tgβcosα.
Из последней выборки видно, что на большом интервале значений β:βb+fy<f, но минимального значения суммарная осевая сила достигает при β=0,5o.
Из этой выборки видно, что второе условие b≥f выполняется при b=1,5o.
Окончательно назначаем угол b для данной передачи b=1,5o.
При выбранном значении угла b=1,5o, полученного на основании настоящей заявки bb+fy= 0,0438, а величина амплитуды переменной составляющей осевой силы fy=0,0177.
Для крайнего значения угла наклона зуба прототипа при β=15' эти величины соответственно равны: bb+fy 0,070, fy=0,065, что в 1,6 и 3,68 раза больше, чем аналогичные значения по настоящей заявке.
Пример 2. Определить оптимальный угол наклона зуба для передачи с параметрами примера 1 при наличии концентрации нагрузки по длине контактной линии: распределение нагрузки по треугольнику (см. фиг.5).
Расчетная часть
1. Так же, как и в примере 1, измерения длины ведется в долях модуля.
2. В целях упрощения расчетов так же, как и в примере 1, условно принимается m 1 мм.
3. В целях упрощения расчетов так же, как в примере 1, условно принимается Ft 1, тогда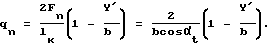
4. По формуле (1) имеем: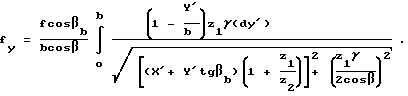
Значения fy= max приведены в табл.2 и взяты из распечаток значений fy в зависимости от угла β, полученных на ЭВМ, для данного численного примера 2.
Из данных табл.2 следует, что минимального значения осевая сила в этом случае, с учетом сил трения, достигает при b=1o.
Второе условие b≥fу выбирается при b=1,75o.
И в этом случае величины суммарной осевой силы bb + fy 0,0513 и осевой переменной составляющей, вызывающей вибрации зубчатых колес в осевом направлении fy 0, 0209 соответственно в 1,38 и 3,2 раза меньше, чем у прототипа со значениями β=15', соответственно равными bb+fy 0,071 и fy 0,067, а выбранное значение угла β 1,75o уже не входит в интервал рекомендуемых в прототипе значений.
Из рассмотренных примеров видно, что предлагаемая косозубая цилиндрическая передача имеет неоспоримое преимущество перед прототипом и в основном рекомендуется для замены прямозубых цилиндрических передач. Это преимущество состоит в снижении максимальной величины осевого усилия, в снижении амплитуды переменной составляющей осевого усилия, что приводит к повышению долговечности подшипниковых узлов, к снижению вибраций в осевом направлении и сопутствующего им шума.
Так как существующие прочностные расчеты дают резкое снижение внутренних динамических сил при переходе от прямозубых цилиндрических передач к косозубым, то предлагаемая передача будет иметь и большую плавность хода по сравнению с прототипом.
Использование: машиностроение. Сущность изобретения: в зубчатой передаче колеса выполнены косозубыми с углом наклона зубьев на делительных цилиндрах, выбранных в пределах 0,1o...3,5o. Использование зубчатой передачи позволяет увеличить долговечность подшипников, снизить габариты и вибрацию в осевом направлении зубчатых колес особенно по сравнению с цилиндрическими прямозубыми передачами. 2 табл.,5 ил.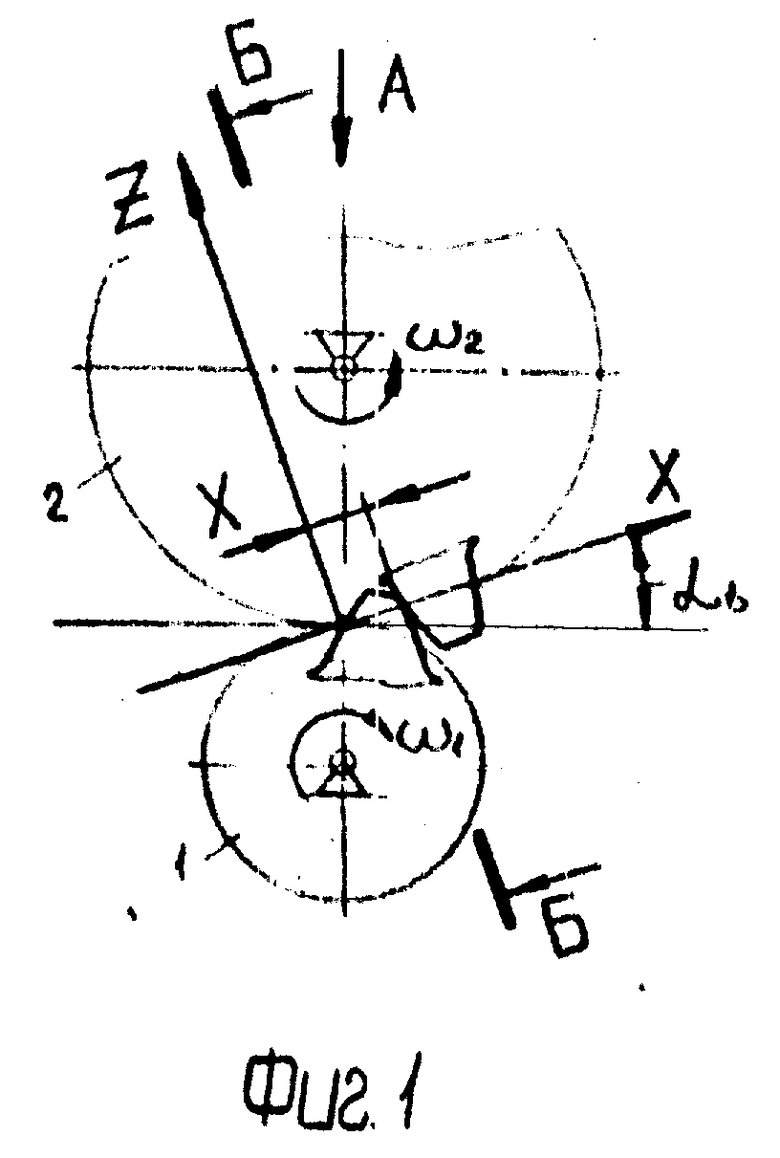
Зубчатая передача, содержащая ведущее и ведомое косозубые цилиндрические колеса, отличающаяся тем, что угол наклона зубьев на делительных цининдрах принимается в пределах 0,1°≤ β ≤ 3,5° и удовлетворяет следующим условиям:
βв + fy < f, β ≥ fy;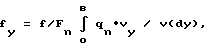
где βв- угол наклона зубьев на основных цилиндрах;
fy приведенная величина коэффициента трения скольжения вдоль мгновенной оси вращения скольжения зубьев;
f коэффициент трения скольжения зубьев;
Fn нормальная сила между контактирующими зубьями;
qn закон распределения нормальной силы по длине контактной линии;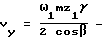 линейная скорость скольжения зубьев вдоль мгновенной оси вращения-скольжения;
линейная скорость скольжения зубьев вдоль мгновенной оси вращения-скольжения;
m нормальный модуль зацепления на начальных цилиндрах;
g - суммарный угол перекоса осей зубчатых колес в плоскости, перпендикулярной межосевому расстоянию;
z1 число зубьев ведущего зубчатого колеса;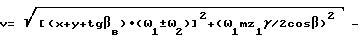 суммарная скорость скольжения в точках контакта зубьев;
суммарная скорость скольжения в точках контакта зубьев;
x и y абсциссы и ординаты точек контактной линии в выбранной системе координат;
ω1 и ω2- угловые скорости соответственно ведущего и ведомого зубчатых колес;
знак (+) для внешнего зацепления, знак (-) для внутреннего зацепления.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Калашников С.Н., Калашников А.С | |||
| Изготовление зубчатых колес | |||
| - М.: Высшая школа, 1980, с.21 | |||
| Иосилевич Б.Г | |||
| Детали машин | |||
| - М.: Машиностроение, 1988, с.166 | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| US, патент, 4294132, кл | |||
| Устройство для электрической сигнализации | 1918 |
|
SU16A1 |
Авторы
Даты
1998-01-20—Публикация
1993-11-04—Подача