Изобретение относится к учебным приборам для демонстрации оптических явлений в курсе физики и представляет собой портативный дифракционный прибор, предназначенный для выявления в ходе демонстрации основополагающего для теории дифракции от решетки влияния числа элементов (щелей) решетки на распределение освещенности в дифракционной картине. Отметим сразу два обстоятельства. 1. Учебный опыт такого рода имеет важное значение в дидактическом плане, поскольку демонстрируемое явление лежит в основе теории широкого класса оптических приборов, включающего дифракционные решетки разных типов, а также другие многолучевые интерференционные оптические системы 2. Необходимые для успешной учебной демонстрации явления устройства не разработаны и в учебной практике отсутствуют.
Наиболее близким по технической сущности к изобретению является учебный прибор по оптике, содержащий источник света, экран и расположенный между ними держатель с диафрагмой и дифракционной решеткой (см. [1], описание авт. св. N SU 1043725 A G 09 B 23/22; авторы С.С.Ветохин, В.Н.Наумчик и М.П. Огриньш: "Учебный прибор по оптике").
Существенным недостатком известного прибора является принципиальная невозможность получения с его помощью протяженной и яркой дифракционной картины, что лишает демонстрацию наглядности и убедительности, а стало быть и дидактической эффективности. Такой вывод однозначно следует из рассмотрения основополагающих закономерностей дифракции света, устанавливающих соответствие между параметрами дифракционной решетки (ширина a одной щели решетки, периодом C, общим числом n щелей), длиной световой волны λ , удалением L решетки от экрана наблюдения Э и размерами дифракционной картины на экране Э. Исходя из этих закономерностей, нетрудно сделать вывод о том, что если параметры известного прибора таковы, что с его помощью формируют достаточно протяженную дифракционную картину (что, вообще говоря, нереально по техническим соображениям), то эта картина должна иметь неудовлетворительную видимость в силу ничтожной ее освещенности. Если же параметры таковы, что картина имеет заметную освещенность (что более реально по техническим соображениям), то она при этом должна оказаться неразличимой в силу неудовлетворительно малых ее размеров. Рассмотрим этот вопрос более подробно, конкретизируя условия опыта. В соответствии с фиг. 3 в описании [1] речь идет о прозрачной дифракционной решетке. Обозначим ширину непрозрачных участков между соседними щелями решетки через b. Тогда постоянную решетки можно представить в виде: c = a + b, где a - ширина одной щели. Из описания [1] следует, что методика работы с известным прибором состоит в том, что в ходе опыта осуществляют диафрагмирование щелей решетки, так сказать, поштучно: сперва открывают одну щель, потом две и т.д. По этой причине ширина ступенек диафрагмирующей пластины (на фиг. 2 в [1] - это пластина 1) должна быть равной c. Но с учетом технических возможностей рабочие края пластины 1 ([1], фиг. 2) вряд ли можно отработать на параллельность с точностью, превосходящей 0,1 мм. К тому же неизбежный люфт диафрагмы 1, перемещаемый вдоль вертикальных направляющих должен сопровождаться неконтролируемым смещением краев диафрагмы, которое вряд ли может быть меньше 0,1 мм на ступень. В силу сказанного не имеет смысла использовать прибор, для которого c <0,2 мм и допустимо положить c ≥ 0,2 мм. Учитывая, что с точки зрения протяженности дифракционной картинки на экране Э предпочтительней оказывается решетка с меньшим возможным значением периода c, примем для определенности, что c = 0,2 мм. Теория дифракции в параллельных лучах (см., например, книги: Ландсберг Г.С. Оптика. -М. : Наука, 1976, 39, 46; Сивухин Д.В. Общий курс физики. Оптика. -М. : Наука, 1980, 45, 46; Савельев И.В. Курс общей физики, т. 2 - М. : Наука, 1978, 129, 130, приводит к известному условию формирования минимумов (нулей) освещенности дифракционной картины от одной щели в виде:
a•sinψK= Kλ ,
где
K - порядок минимума (темной полосы) от одной щели, K = 1, 2, 3... ; ψK - угол дифракции, соответствующий этому минимуму. В частности для первого минимума освещенности имеем
a•sinψ1= λ (1)
Вместе с тем, теория дифракции в параллельных лучах от решетки (в данном случае - от нескольких эквидистантных щелей) дает условие формирования главных дифракционных максимумов в виде
c•sinψm= mλ, (2)
где
ψm - угол дифракции, соответствующий m-му главному максимуму. Из приведенного в описании [1] на фиг. 5 распределения освещенности видно, что главный дифракционный максимум второго порядка (m = 2) в картине от двухщелевой решетки приходится на первый минимум от одной щели. Сопоставление формул (1) и (2) с учетом, что ψm= ψ1 , дает для приведенного случая: a = c/2. Полагая c = 0,2 мм, будем иметь a = 0,1 мм. Угловая область Δψ , в пределах которой распределяется подавляющая часть проходящего через решетку светового потока простирается между первыми нулями освещенности картины дифракции от одной щели, т.е. Δψ = 2ψ1= 2arcsin(λ/a) . Поскольку λ ≪ a (при λ = 6•10-7 м и a = 10-4 имеем: λ/a = 6•10-3) допустимо принять arcsin(λ/a) = λ/a и Δψ = 2λ/a . Вводя расстояние L от решетки до экрана Э, может выразить поперечную протяженность ΔX дифракционной картины в области Δψ в виде: ΔX = LΔψ = 2Lλ/a. . Полагая L = 2 м, λ = 6•10-7 м и a = 10-4 м, получим ΔX = 12 мм, что для демонстрационного опыта совершенно недостаточно и совершенно неприемлемо. Этот результат и представляет собой количественное обоснование высказанного выше утверждения о невозможности достижения посредством известного прибора необходимой наглядности демонстрации.
Отмеченные существенные недостатки известного прибора полностью устранены в предлагаемом учебном приборе по оптике. Принципиальное отличие предлагаемого прибора от известного состоит в том, что в предлагаемом приборе используются дифракционные решетки, которые состоят из структурных элементов - ячеек, имеющих соответственно двухточечную, трехточечную или в общем случае n-точечную структуру. Обозначим общее число ячеек в данной дифракционной решетке через N. Все эти N ячеек имеют одну и ту же структуру, т.е. одно и то же число одинаковых в пределах данной ячейки точек при одинаковом как по величине, так и по направлению смещения lo между соседними элементами (точками) ячейки. При этом расстояние liK между соседними ячейками в пределах поверхности дифракционной решетки изменяется совершенно хаотически. При освещении такой дифракционной решетки и соответствующих условиях наблюдения дифракционной картины имеют место для эффекта: 1) одинаковый дифракционно-интерференционный эффект от каждой из N ячеек и 2) изменяющийся в зависимости от величины liK эффект взаимной (межячеечной) интерференции от разных ячеек. В силу хаотичесности значений параметра liK в пределах освещенной поверхности дифракционной решетки эффект межячеечной интерференции практически полностью стирается, тогда как постоянство параметра lo приводит к наслоению и N-кратному усилению одинаковых дифракционных картин от множества одинаковых ячеек. Это позволяет получить контрастную дифракционную картину большой протяженностью и яркости, вид которой и распределение в ней освещенности определяется числом точек в ячейке. Технология изготовления дифракционных решеток, используемых в предлагаемом учебном приборе по оптике, состоит в том, что на фотопластинку высокого разрешения двухкратно, трехкратно или в общем случае n-кратно фотографируют одну и ту же спекл-картину в спекл-поле, формируемом лазерным излучением, рассеянным матовой поверхностью. Фотографирование осуществляется при эквидистантном и однонаправленном смещении фотопластинки между экспозициями. Такая технология позволяет получить дифракционные решетки с двухточечными или многоточечными ячейками при очень малых размерах d точек и достаточно малых значениях параметра lo. Поэтому, наряду с большой освещенностью дифракционной картины за счет многократного усиления эффекта, эта картина имеет и большие размера за счет малости параметров d и lo .
Указанные специфические особенности дифракционных решеток, используемых в предлагаемом учебном приборе по оптике, и позволяет получить и продемонстрировать светосильную, т.е. протяженную и яркую картину дифракции от двухточечного (опыт Юнга), трехточечную и в общем случае - многоточечную (вплоть до n = 20) объекта в условиях резко выраженного и отчетливо наблюдаемого влияния числа n на распределение освещенности в дифракционной картине, приводящего к характерной деформации этой картины. Сделанные выше оценки приводят к однозначному выводу о том, что указанный результат принципиально недостижим при использовании одиночного объекта дифракции, состоящего из двух, трех или в общем случае - из n элементов (точек, щелей). Он недостижим, в частности, и при использовании известного учебного прибора по оптике.
Конструкция предлагаемого учебного прибора по оптике поясняется фиг. 1. Прибор включает держатель 1 на стержне-стойке 2. Внутренняя круглая подвижная оправа 3 держателя имеет в средней части квадратное отверстие размером 3,7 • 3,7 см. Способная поворачиваться в своей плоскости эта оправа 3 имеет направляющие 4, в которые встроена плоская обойма 5 с внешними размерами 5 • 35 см и прямоугольным внутренним вырезом размером 3,8 • 25 см, содержащая расположенные друг за другом пять дифракционных решеток 6 с ячеистой структурой. Дифракционные решетки имеют размер 4,8 4,8 см при n = 2, 3, 4, 6, 10. Вставленные в обойму, дифракционные решетки 6 удерживаются бортами обоймы и крепящим винтиком 7. Обойма с дифракционными решетками может свободно перемещаться по направляющим 4 оправы, при этом в момент расположения каждой из дифракционных решеток против отверстия-окна оправы 3 имеет место мягкая фиксация обоймы, сопровождающаяся слабым щелчком. Жесткая фиксация обоймы достигается при помощи крепящего винта 8. Имеющие квадратную форму дифракционные решетки вырезаны из фотопластинок со спекл-картиной так, чтобы цепочки ячеек были ориентированы параллельно одному из краев своего квадрата. Для предохранения от повреждений и удобства в эксплуатации каждая из дифракционных решеток покрыта прозрачной пластинкой тонкого стекла того же размера и окантована по краям полосками черной бумаги так, чтобы открытая часть пластинки имела размеры 3,8 • 3,8 см. Дифракционные решетки вставлены в обойму с таким расчетом, чтобы цепочки ячеек простирались параллельно длине обоймы при горизонтальной ориентации направляющих оправы и чтобы число n от решетки к решетке изменялось монотонно.
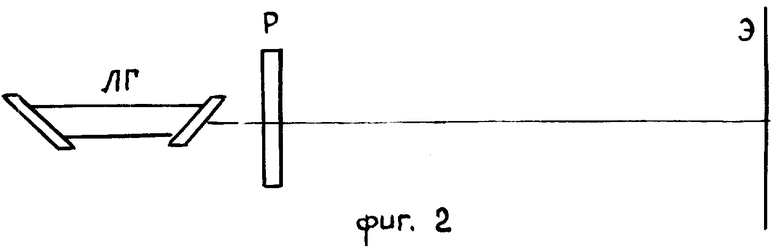
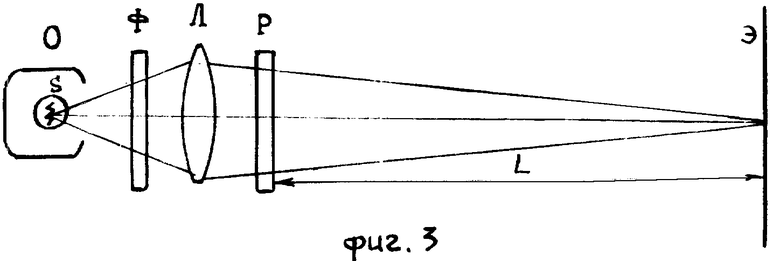
В лазерном пучке опыт выполняют по схеме фиг. 2: здесь ЛГ-газовый лазер непрерывного действия, Р - учебный прибор по оптике с ячеистой дифракционной структурой. Э - экран наблюдения, удаленный на несколько метров от прибора Р. В свете лампы накаливания опыт выполняют по схеме фиг. 3: здесь О - осветитель с маломощной лампой накаливания на 21 Вт (12 В), имеющий прямую спиральную нить (длина нити около 6 мм, диаметр витков спирали около 0,6 мм); Ф - съемный светофильтр (оранжевое или светлокрасное стекло), Р-прибор, Э-экран, Л-линза (F=20 см), фокусирующая изображение нити S на экран Э, удаленный от прибора Р на базисное расстояние L = 2-3 м. При выполнении опыта по схеме фиг. 3 сначала фокусируют изображение нити S на экран Э при выведенной из светового пучка обойма с дифракционными решетками, а затем вводят обойму, передвигая ее, последовательно помещают в световой пучок дифракционные решетки, для которых n = 2, 3, 4, 6, 10 и демонстрируют влияние числа n на распределение освещенности в дифракционной картине. Целесообразно сперва показать опыт с оранжевым светофильтром, а потом удалить светофильтр и, повторяя опыт в белом свете, продемонстрировать картину в виде системы ярких и красочных хроматических полос. Графики фиг. 4а-г в сопоставлении со снимками фиг. 5а-г наблюдаемых в опытах дифракционных картин, иллюстрируют достигаемые при помощи предлагаемого учебного прибора по оптике результаты.
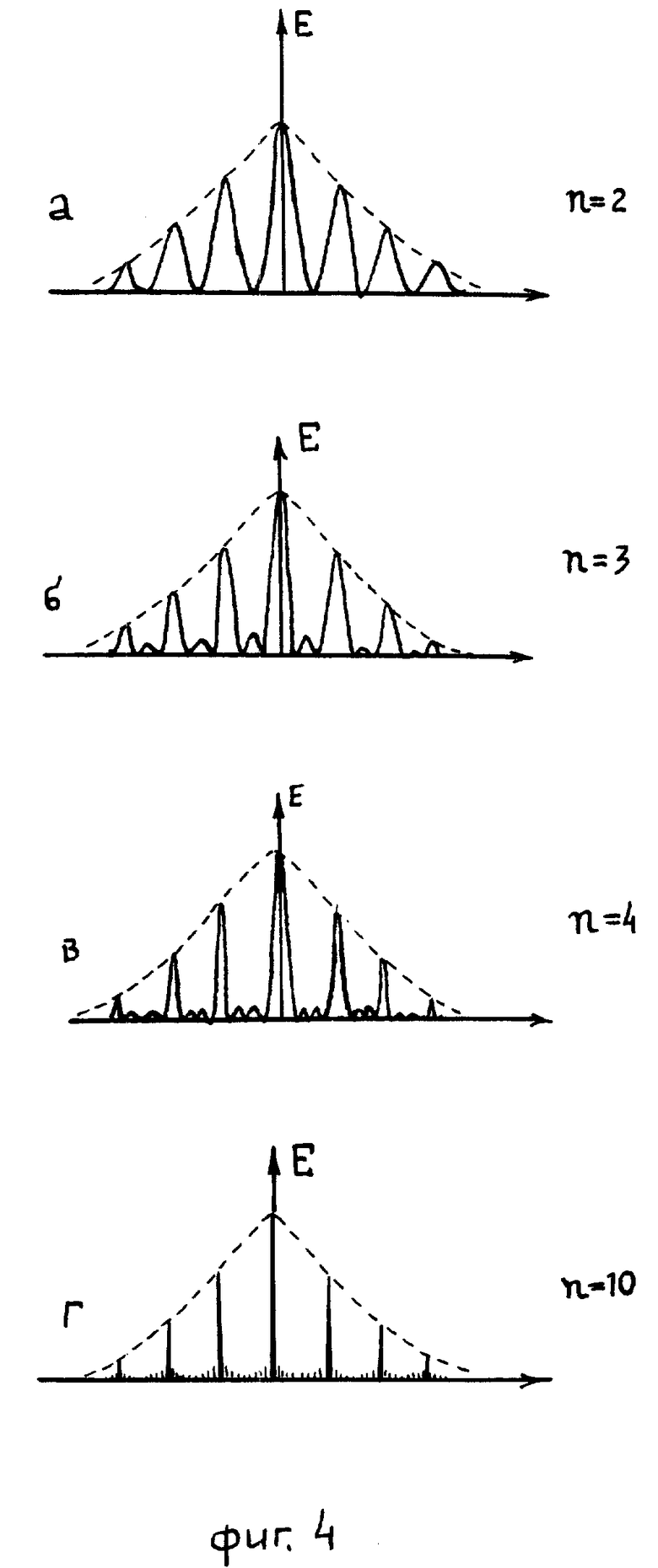
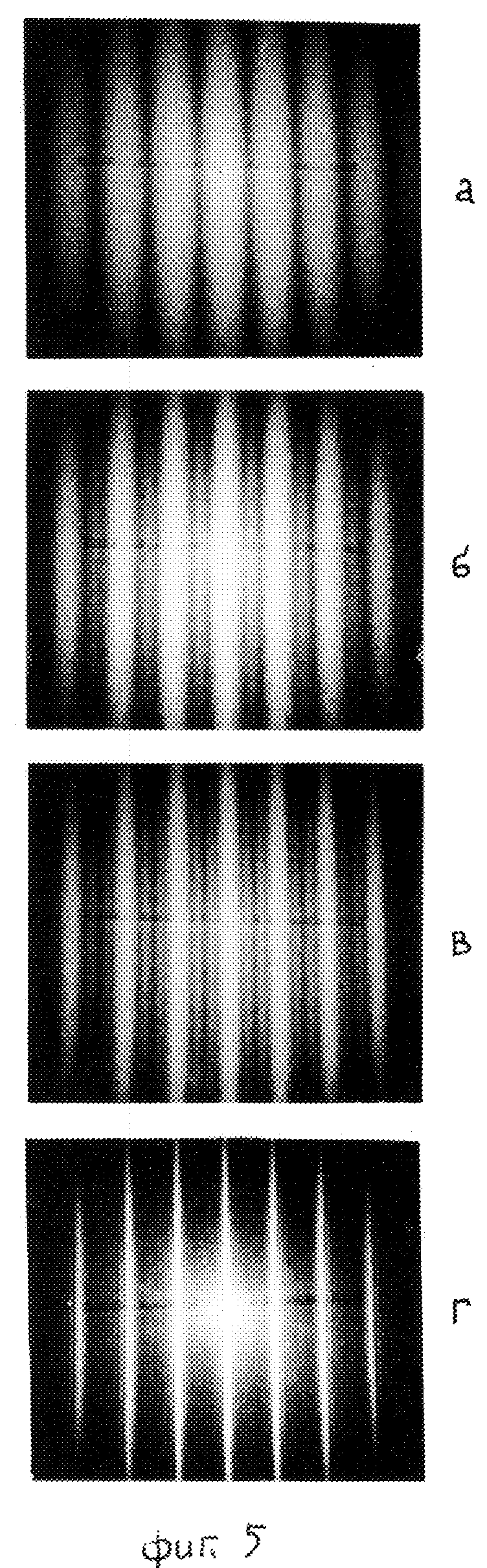
На фиг. 4 приведены графики распределения освещенности в дифракционной картине на экране Э в направлении, перпендикулярном к длине полос при n = 2, 3, 4, 10, соответствующие известной теории явления (заметим, что при n = 2 картина представляет собой систему полос Юнга). Согласно этой теории при увеличении числа n происходит сужение главных дифракционных максимумов освещенности, ширина которых h ≈ 1/n, и появление между соседними главными максимумами слабых вторичных максимумов, число которых n' = n-2. Наблюдаемые при помощи предлагаемого учебного прибора по оптике дифракционные эффекты (фиг. 5а-г) убедительно и полностью подтверждают эти важные выводы теории. Снимки фиг. 5а-г получены в опытах, выполненных по схеме фиг. 2: источник света гелий-неоновый лазер ЛГ-75, базисное расстояние L=5 м, картина снята с большого экрана, поперечные размеры дифракционного поля на экране Э превосходят 1,5 м, а расстояние между полосами H ≅ 20 см.
Предлагаемый учебный прибор по оптике позволяет выполнить все опыт этой важной демонстрации быстро и эффективно. Положительный эффект использования предлагаемого прибора состоит в том, что он дает возможность получить протяженную и яркую картину явления, основополагающего для теории многих оптических приборов. Светосильность прибора обеспечивает наглядность и убедительность демонстрации и ее дидактическую эффективность.
| название | год | авторы | номер документа |
|---|---|---|---|
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1995 |
|
RU2077073C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЛИНЕЙНОЙ ДИСПЕРСИИ ПРИЗМЕННОГО СПЕКТРАЛЬНОГО ПРИБОРА | 1994 |
|
RU2082115C1 |
| УЧЕБНЫЙ ОПТИЧЕСКИЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР | 2001 |
|
RU2206064C2 |
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1996 |
|
RU2114462C1 |
| УЧЕБНЫЙ ОПТИЧЕСКИЙ ИНТЕРФЕРОМЕТР | 1998 |
|
RU2154307C2 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С КРИСТАЛЛОМ ИСЛАНДСКОГО ШПАТА | 2001 |
|
RU2219490C2 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С ОДИНОЧНОЙ ПРОЗРАЧНОЙ ПЛАСТИНОЙ | 2011 |
|
RU2463666C2 |
| Учебный прибор по оптике | 1983 |
|
SU1156115A1 |
| Способ изготовления интерференционного учебного прибора | 1987 |
|
SU1503036A1 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С КРИСТАЛЛООПТИЧЕСКОЙ СИСТЕМОЙ | 2003 |
|
RU2250436C1 |
Прибор содержит набор дифракционных решеток с разными структурными характеристиками и выполнен с возможностью их последовательной установки в окне диафрагмы. Дифракционные решетки изготовлены посредством многократного фотографирования на фотопластинку высокого разрешения одной и той же спекл-картины при эквидистантном и однонаправленном перемещении фотопластинки между экспозициями и при разной кратности экспозиций. Прибор позволяет получить протяженную и яркую картину дифракции. 5 ил.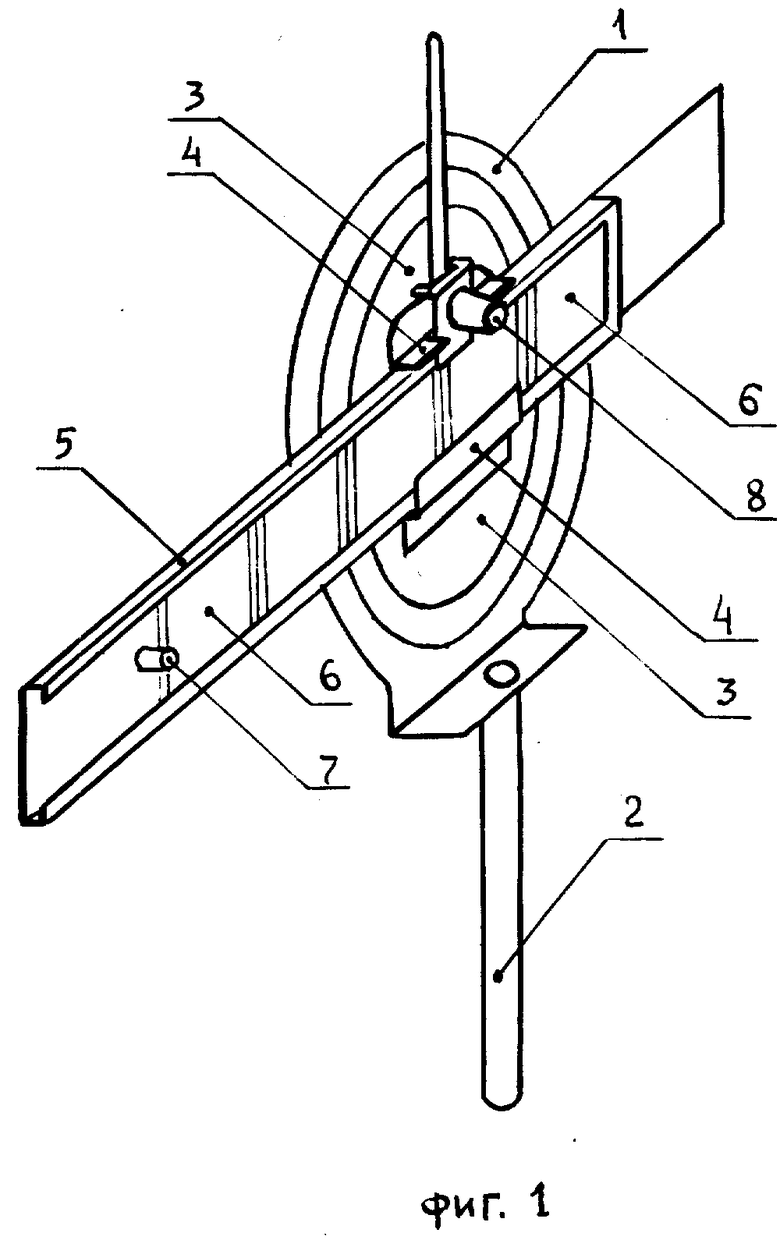
Учебный прибор по оптике, содержащий источник света, экран и расположенный между ними держатель с диафрагмой и дифракционной решеткой, отличающийся тем, что дифракционная решетка установлена в обойме, содержащей набор дифракционных решеток с разными структурными характеристиками, обойма имеет возможность перемещения и фиксации относительно диафрагмы с последовательной установкой дифракционных решеток в окне диафрагмы, а дифракционные решетки изготовлены посредством многократного фотографирования на фотопластинку высокого разрешения одной и той же спекл-картины при эквидистантном и однонаправленном перемещении фотопластинки между экспозициями и при разной кратности экспозиций.
| Учебный прибор по оптике | 1982 |
|
SU1043725A1 |
Авторы
Даты
1998-05-27—Публикация
1996-04-11—Подача