Как известно, возникновение интерференционной картины в любом интерференционном приборе обусловлено перекрыванием когерентных световых пучков. Перекрывание световых пучков обеспечивается конструкцией самого прибора, а когерентность - выполнением ряда требований, предъявляемых к используемому в приборе источнику света, и юстировкой самого прибора.
Так, для достижения пространственной когерентности перекрывающихся пучков необходимо в должной степени ограничить размеры источника света. Во многих интерференционных схемах в качестве источника света используют ярко освещенную щель. Расчет (см., например, книги: [1] Ландсберг Г.С. Оптика. -М. : Наука, 1976, 928 с., с.82. [2] Сивухин Д.В. Общий курс физики. Оптика. - М.: Наука, 1980, 752 с., с.207. [3] Калитеевский Н.И. Волновая оптика. -М. : Высшая школа, 1978, 480 с., с.156) приводит в этом случае к условию пространственной когерентности в виде:
a•tg2u≤λ/2, (1)
где λ - длина световой волны, а - ширина щелевого источника света, а 2u - апертура интерференции, т.е. угол между двумя лучами, исходящими из одной точки источника, которые после прохождения интерференционного прибора перекрываются в данной точке поля наблюдения.
Для достижения временной когерентности в области перекрывания необходимо в должной степени монохроматизировать освещающий пучок. Расчет (см., например, [1] с. 92; [2] с.220; [3] с.185) приводит к условию временной когерентности в виде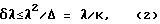
где Δ - разность хода интерферирующих лучей, 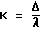 - целочисленный порядок интерференции, а δλ - допустимая степень немонохроматичности используемого излучения - ширина его спектрального интервала. При наблюдении картины в белом свете набор длин волн δλ захватывает всю видимую часть спектра. Высококонтрастная система интерференционных полос в этом случае может формироваться только в той части интерференционного поля (если таковая существует), которой соответствуют полосы самых первых порядков К=0, 1, 2......
- целочисленный порядок интерференции, а δλ - допустимая степень немонохроматичности используемого излучения - ширина его спектрального интервала. При наблюдении картины в белом свете набор длин волн δλ захватывает всю видимую часть спектра. Высококонтрастная система интерференционных полос в этом случае может формироваться только в той части интерференционного поля (если таковая существует), которой соответствуют полосы самых первых порядков К=0, 1, 2......
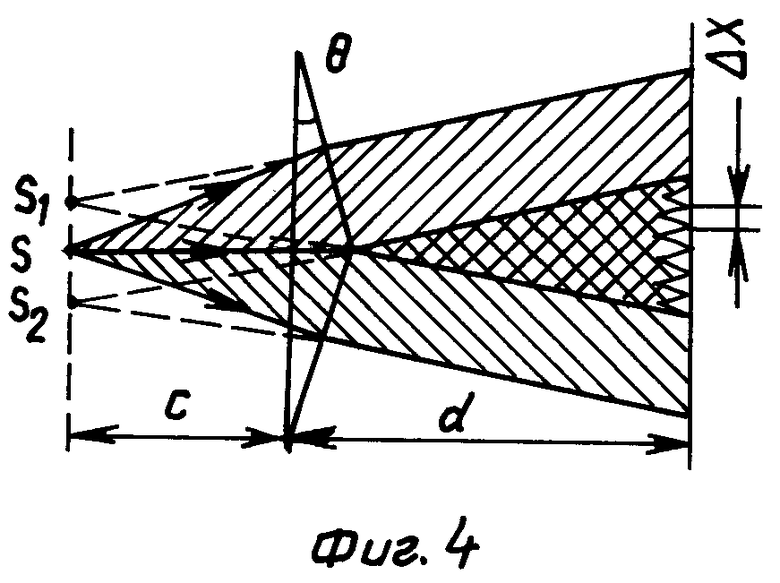
Трудности, обусловленные малостью длины световой волны λ, приводят к тому, что в учебной практике удается успешно использовать лишь очень небольшое число интерференционных приборов. Одним из них является бипризма Френеля. Описание устройства работы и практического приложения бипризмы Френеля в учебных целях см., например, в книгах: [4] Савельев И.В. Курс общей физики, т. 2. -М.: Наука, 1978, 480 с., с.351-352, рис.121.2, формула 121,3; [5] Демонстрационный эксперимент по физике в средней школе, ч. 2 (под ред. А. А.Покровского). -М.: Просвещение, 1979, 288 с., с.188-192. Схема расположения бипризмы Френеля в световом пучке от источника S в соответствии с [4] с.351, рис.121.2 представлена на фиг.4.
При соблюдении условия пространственной когерентности (1) бипризма Френеля формирует в белом свете интерференционную картину в виде семейства прямых хроматических полос первых порядков с ахроматической центральной нулевой полосой. Расчет ширины ΔХ полос картины, полученной в монохроматическом свете с длиной волны λ, приводит к формуле
ΔX = (C+d)•λ/[2C(n-1)•Θ], (3)
где С и d - расстояния, указанные на чертеже, n - абсолютный показатель преломления материала бипризмы, а Θ - преломляющий угол бипризмы (см. [4], с.352, формула 121.3).
К важным в плане дидактики обучения недостаткам бипризмы Френеля, как учебного прибора, можно отнести следующие.
1. Для расчета разности хода Δ перекрывающихся лучей необходимо вводить фиктивные (мнимые) источники света S1 и S2, заменяющие реальный источник S. Это лишает расчет наглядности и очевидности.
2. Сам расчет, как и вытекающая из него формула (3), оказывается громоздким.
3. В ходе опытов с бипризмой Френеля можно посредством прямых и простых измерительных операций измерить ширину полос ΔХ (при помощи окулярного микрометра) и расстояния С и d (при помощи линейки). Но остаются еще три входящие в (3) величины: Θ, n и λ. Экспериментальная учебная задача может заключаться в отыскании одной из этих трех величин, например, λ. Для ее решения требуется измерить две другие величины: n и Θ. Но для выполнения измерений такого рода нужны специальные измерительные приборы. Отсюда громоздкость измерительной методики при использовании бипризмы Френеля, как учебного измерительного прибора, и ограниченность возможностей этого прибора.
Предлагаемый в данной заявке и описываемый ниже учебный оптический измерительный прибор прост по конструкции и доступен в изготовлении, а природа наблюдаемой в учебном оптическом интерференционном приборе картины и вывод рабочей формулы отличается наглядностью. Таким образом, предлагаемый прибор лишен тех недостатков, которые присущи бипризме Френеля.
Схема расположения оптических деталей в приборе приведена на фиг.1. Здесь S - лампа накаливания в кожухе осветителя Ос, которая освещает щель Щ шириной а, выполняющую роль одномерного источника света; Пл - засвеченная слабопрозрачная фотопластинка с прорезом Пр шириной b в слое эмульсии Э (толщина слоя эмульсии t, показатель преломления n, коэффициент пропускания (по интенсивности) Т). Пластинку Пл удаляют от щели Щ на расстояние С и ориентируют так, чтобы прорез Пр оказался параллельным щели Щ. Картину наблюдают в плоскости I-I - фокальной плоскости окуляра Ок, удаленной от Пл на расстояние d.
В соответствии с фиг.1 в точку А2 плоскости наблюдения I-I приходят и здесь перекрываются два луча, исходящие из одной и той же точки О источника света - щели Щ под углом 2u (2u - апертура интерференции; для описываемой установки, как показывает количественный расчет и опыт, имеем 2u≅0,005). Первый из них луч OO1А2 идет от точки O к точке O1 прореза Пр и далее в результате дифракции на прорезе изменяет направление распространения на угол ψ и идет по направлению O1А2. Этот луч толщу t прореза проходит в воздухе (n0= 1). За счет дифракции на прорезе интенсивность II дифрагированного O1А2 уменьшается по сравнению с интенсивностью первичного луча OO1.
Второй луч OА1А2 идет от точки O в точку А2 напрямик через слой эмульсии, также имеющей толщину t, но показатель преломления n(n>1). Луч А1А2 также оказывается ослабленным по сравнению с первичным лучом OА1, но по другой причине - за счет поглощения в засвеченном слое фотоэмульсии.
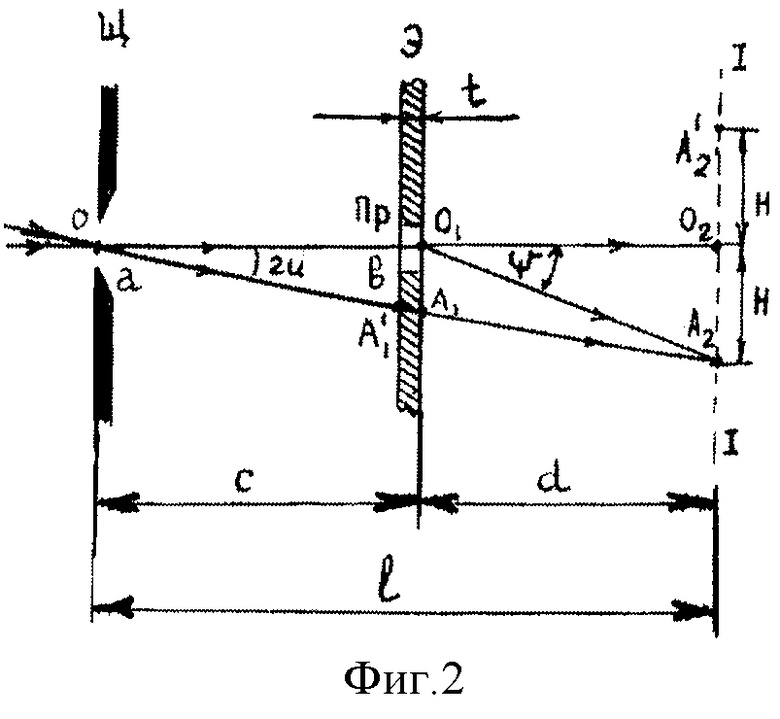
Для упрощения дальнейших выкладок оценим влияние на оптические пути лучей OO1А2 и OА1А2 самой подложки П. Первый из лучей проходит подложку нормально к поверхности подложки и его оптический путь в подложке составляет tпnп, где tп - толщина подложки, а nп - ее показатель преломления. Второй луч проходит подложку под углом 2u/nп к нормали и его путь в подложке составляет tпnп[1+(2u/nп)2]1/2=tпnп[1+(2u/nп)2/2]. Различие этих путей δΔп = tп(2u)2/2nп. При tп=1,2 мм, 2u=0,005 рад и nп=1,5 имеем δΔп≅0,01 мкм, что представляет собой величину пренебрежимо малую даже по сравнению с длиной световой волны λ. Поэтому влияние подложки можно не учитывать и производить подсчеты величины Δ, полностью исключив подложку из рассмотрения, т.е. исходя из схемы расположения оптических деталей прибора, приведенной на фиг.2.
Интенсивность II первого луча O1А2 зависит от угла дифракции ψ и по мере увеличения угла ψ, сопутствующего увеличения смещения Н=O2А2, интенсивность II заметно изменяется. Интенсивность I2 второго луча А1А2, ослабленного за счет поглощения в эмульсии, определяется плотностью почернения фотослоя и по мере удаления точки А2 от точки O2 интенсивность I2 не изменяется. Поэтому появляется возможность отыскать такое место в области перекрывания, в котором интенсивности обоих лучей оказываются одинаковыми.
Геометрический путь первого луча определяется ломаной линией OO1А2, причем, весь этот путь первый луч проходит в воздухе. Поэтому оптический путь первого луча совпадает с длиной этой ломаной OO1А2. Геометрический путь второго луча определяется прямой линией OА1А2, которая короче ломаной OO1А2. Но часть этого пути второй луч проходит в толще фотоэмульсии, имеющей показатель преломления n>1, и испытывает дополнительное запаздывание, определяемое величиной t(n-1). Таким образом, оптический путь второго луча оказывается больше отрезка OА2А2 на величину t(n-1). Поэтому при данных значениях t и n всегда можно отыскать такое место картины, например, вблизи точки А2, для которого разность хода лучей оказывается близкой к нулю. Если перекрывающиеся здесь лучи будут при этом характеризоваться и высокой степенью пространственной когерентности, то произойдет их интерференция и вблизи точки А2 будут формироваться полосы самых первых интерференционных порядков с центральной нулевой полосой. А такую картину можно наблюдать в белом свете.
Картина эта будет иметь высокую контрастность, если одновременно выполняются следующие условия.
1. Ширина а щели Щ оказывается малой в такой степени, что для точки А2 выполняется условие (1) пространственной когерентности.
2. Разность хода Δ в точке А2 оказывается достаточно малой (Δ≅0); в соответствии с условием (2) это обеспечивает высокую степень временной когерентности перекрывающихся лучей.
3. Интенсивности II и I2 этих лучей, один из которых ослаблен за счет дифракции, а другой - за счет поглощения в слое фотоэмульсии, оказываются близкими по величине: I1≅I2.
Вместе с тем, необходимо, чтобы была достигнута высокая степень параллельности щели Щ и прореза Пр и чтобы сам прорез и слой фотоэмульсии в области прореза имели высокую степень однородности по параметрам b и t.
С целью конкретизации необходимых условий подсчитаем разность хода Δ перекрывающихся в точке А2 лучей. Из фиг.2 следует, что
Δ = OA1A2+t•(n-1)-OO1A2 (4)
Учтем введенные ранее обозначения: OO1=С, OO2=l, O1O2=d, O2А2=Н. Тогда на основании фиг.2 и простых алгебраических преобразований с использованием теоремы Пифагора можем записать
OO1A2=С+(d2+H2)1/2=C+d[1+(Н/d)2]1/2, (5)
OА1А2=(l2+H2)1/2=l[1+(H/l)2]1/2, (6)
Принимая во внимание малость отношений (Н/d) и (Н/l) (и то и другое не превосходит 0,01), перепишем соотношения (5) и (6) в виде
OO1A2=С+d[1+(Н/d)2/2]=l+H2/2d, (7)
OА1А2=l[1+(H/l)2/2]=1+H2 /2l, (8)
Подставляя соотношения (7) и (8) в (4), получим
Обозначим смещение нулевой полосы, для которой К=0 и Δ = Kλ = 0, через Но. Для нулевой полосы (9) запишется в виде
t•(n-1)-H0 2•С/(2ld)=0, (10)
В белом свете нулевая полоса оказывается ахроматической и, имея высокую контрастность, заметно выделяется в интерференционной картине. Придадим соотношению (10) вид
n=1+H0 2C/(2t•l•d), (11)
Все величины, входящие в правую часть соотношения (11), можно измерить: расстояния С, d и l= C+d - посредством линейки, смещение Но - при помощи окулярного микрометра, а толщину t - оптиметром. Поэтому формула (11) позволяет оценить показатель преломления n поглощающего слоя.
Ширина полос интерференционной картины или иначе - расстояние h между соседними полосами картины зависит от смещения Н. Опыт показывает и расчет это подтверждает, что с увеличением Н ширина полос убывает. Больший интерес представляет оценка ширины полос h≅h0 в области максимальной контрастности картины, т. е. - вблизи нулевой полосы, для которой Н Н0. Для такой оценки воспользуемся соотношением (10), определяющим положение нулевой полосы, и соотношением (9), записанным для полосы первого порядка (К=1, Δ = λ), прилегающей изнутри к нулевой полосе (Н=Н0-h0). Вычитая из второго соотношения первое, получим
Н0. Для такой оценки воспользуемся соотношением (10), определяющим положение нулевой полосы, и соотношением (9), записанным для полосы первого порядка (К=1, Δ = λ), прилегающей изнутри к нулевой полосе (Н=Н0-h0). Вычитая из второго соотношения первое, получим
h0(2H0-h0)•C/(2l•d) = λ. (12)
Учитывая, что h0<<2Н0, можем записать приближенно
h0 = λld/(H0C). (13)
В случае, когда d=C формулы (11) и (13) упрощаются и принимают вид
n=1+H0 2/(2t•l), (11а)
h0 = λl/H0, (13a)
Оценим теперь допустимую ширину a щели Щ. Из фиг.2 имеем: tg 2u=H0/l, поэтому условию (1) можно придать вид
a≤λl/(2H0). (14)
Третье из упомянутых выше условий требует равенства интенсивностей I1=I2 перекрывающихся пучков. Это достигается подбором коэффициента пропускания Т пластинки Пл.
Для достижения одинаковой контрастности полос по обе стороны дифракционного поля необходимо, чтобы прорез Пр по всей длине своей рабочей части не имел сужений и расширений, т.е. таких мест, где противоположные края прореза не параллельны друг другу. Важно также, чтобы прорез не имел зазубрин и чтобы толщина поглощающего слоя оставалась одинаковой в пределах рабочей части прореза. Поэтому в подготовленной засвеченной фотопластинке с подходящим коэффициентом пропускания Т канавку-прорез проделывают при помощи острого без зазубрин ножа (лучше - скальпеля) и стальной линейки при несильном и однородном давлении на нож.
Учебный оптический интерференционный прибор собирают на оптической скамье. Конденсатор осветителя удаляют и вплотную к кожуху осветителя с кинопроекционной лампой придвигают раздвижную щель Щ, закрепленную в стандартном держателе на высоте спирали лампы. Из подготовленной засвеченной фотопластинки Пл с прорезом Пр при помощи стеклореза вырезают квадратный участок размером 50•50 мм2 с прорезом вдоль средней линии квадрата. Эту светоделительную часть прибора закрепляют в стандартной оправе, позволяющей плавно поворачивать препарат в своей плоскости, т.е. вокруг оси светового пучка, и закрепляют стойку оправы в ползунке оптической скамьи так, чтобы щель Щ и прорез Пр были ориентированы вертикально и их центры находились на одной горизонтальной оси.
Для достижения картины хорошего качестве необходимо добиться высокой степени параллельности Щ и Пр. Поэтому в ходе юстировки учебного оптического интерференционного прибора после грубой - на глаз - установки пластинки Пл на параллельность Пр и Щ необходимо, рассматривая интерференционную картину в окуляр прибора, собранного по схеме фиг.1, очень медленно методом малых смещений, практически почти плавно, поворачивать пластинку Пл вокруг оси пучка и добиться максимальной контрастности картины.
Пластинку Пл удаляют от щели Щ на расстояние С=0,2 м, а окуляр Ок с микрометрической шкалой, имеющей цену деления 0,1 мм, закрепляют в стандартном держателе на высоте оси светового пучка и устанавливают на расстоянии d÷(0,1-0,3) м от Пр.
Предметом учебного опыта может являться наблюдение самой необычайной дифракционно-интерференционной картины и изучение феноменологии возникновения двух симметрично расположенных относительно средней линии дифракционного поля систем хроматических интерференционных полос высокой контрастности. Вместе с тем, учебный интерес представляет выполнение необходимых измерений и проведение расчетов с использованием формул (11), (13), (14).
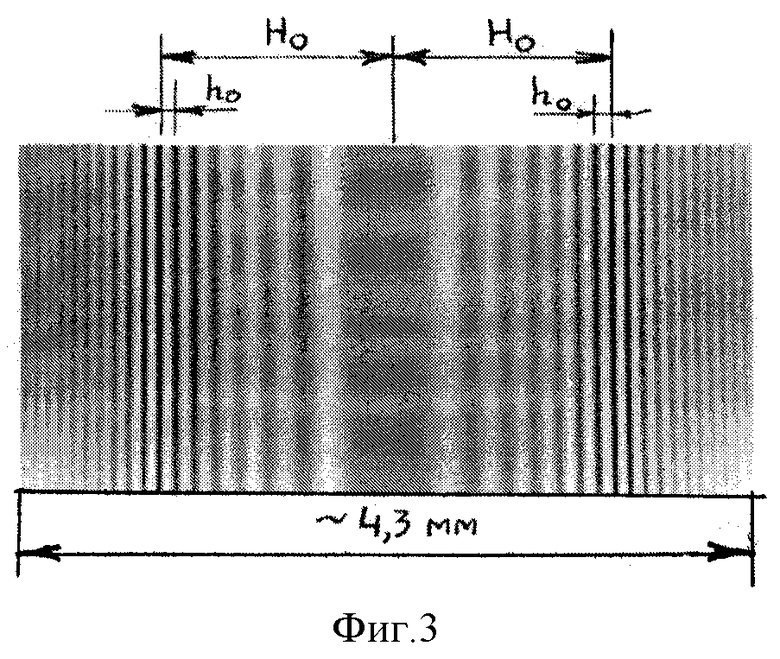
В одном из наших опытов при С=d=0,2 м измерения дали: Н0=2,15 мм. Принимая для средней части видимой области спектра λ=540 нм, получим на основании (13а) и (14): h0=0,1 мм и a≤0,05 мм. Вместе с тем, при t=11 мкм и l=0,4 м на основании (11а) имеем n≅1,52.
На фиг. 3 представлена интерферограмма, иллюстрирующая явление. Снимок сделан в белом свете (без светофильтра) при следующих параметрах установки: a≅0,03 мм, b≅0,02 мм, С=0,2 м, d=0,1 м, t≅11 мкм, Н0=1,35 мм, Т=0,0035.
| название | год | авторы | номер документа |
|---|---|---|---|
| УЧЕБНЫЙ ОПТИЧЕСКИЙ ИНТЕРФЕРОМЕТР | 1998 |
|
RU2154307C2 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С КРИСТАЛЛОМ ИСЛАНДСКОГО ШПАТА | 2001 |
|
RU2219490C2 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С КРИСТАЛЛООПТИЧЕСКОЙ СИСТЕМОЙ | 2003 |
|
RU2250436C1 |
| УЧЕБНЫЙ ИНТЕРФЕРЕНЦИОННЫЙ ПРИБОР С ОДИНОЧНОЙ ПРОЗРАЧНОЙ ПЛАСТИНОЙ | 2011 |
|
RU2463666C2 |
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1996 |
|
RU2112283C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЛИНЕЙНОЙ ДИСПЕРСИИ ПРИЗМЕННОГО СПЕКТРАЛЬНОГО ПРИБОРА | 1994 |
|
RU2082115C1 |
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1996 |
|
RU2114462C1 |
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1995 |
|
RU2077073C1 |
| Учебный прибор по оптике | 1991 |
|
SU1781694A1 |
| Учебный прибор по оптике | 1987 |
|
SU1481843A1 |
Учебный оптический интерференционный прибор состоит из осветительной части, содержащей лампу накаливания и щель, выделяющую узкий световой пучок, светоделительной системы, формирующей два когерентных перекрывающихся пучка белого света одинаковой интенсивности, и наблюдательной части в виде окуляра с окулярным микрометром. Светоделительная система представляет собой слабопрозрачный слой оптически плотной среды с узким прорезом в виде щелевидной прозрачной воздушной полости и формирует два перекрывающихся световых пучка, один из которых возникает за счет дифракционного расширения части первичного пучка с ослаблением интенсивности пучка в результате дифракции на воздушной полости, а второй возникает за счет сквозного прохождения другой части первичного пучка через слабопрозрачный слой с ослаблением интенсивности пучка за счет поглощения в слое, при этом в интерференционном слое при определенных параметрах установки и поглощающего слоя формируется картина, в которой образуются две системы хроматических полос первых порядков, симметрично смещенные относительно средней линии интерференционного поля. Технический результат - простота конструкции и доступность изготовления. 4 ил.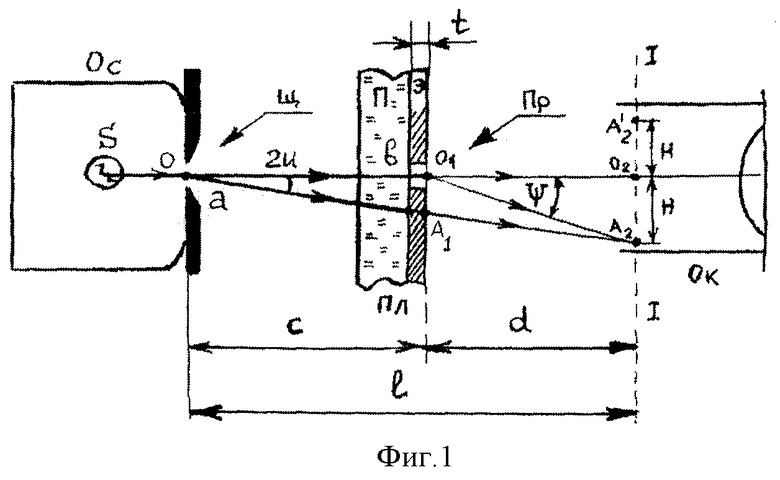
Учебный оптический интерференционный прибор, состоящий из осветительной части, содержащей лампу накаливания и щель, выделяющую узкий световой пучок, светоделительной системы, формирующей два когерентных перекрывающихся пучка белого света одинаковой интенсивности, и наблюдательной части в виде окуляра с окулярным микрометром, отличающийся тем, что светоделительная система представляет собой слабопрозрачный слой оптически плотной среды с узким прорезом в виде щелевидной прозрачной воздушной полости и формирует два перекрывающихся световых пучка, один из которых возникает за счет дифракционного расширения части первичного пучка с ослаблением интенсивности пучка в результате дифракции на воздушной полости, а второй возникает за счет сквозного прохождения другой части первичного пучка через слабопрозрачный слой с ослаблением интенсивности пучка за счет поглощения в слое, при этом в интерференционном слое при определенных параметрах установки и поглощающего слоя формируется картина, в которой образуются две системы хроматических полос первых порядков, симметрично смещенные относительно средней линии интерференционного поля, причем величина смещения высококонтрастной центральной ахроматической полосы в каждой из двух систем однозначно связана с показателем преломления поглощающей среды.
| САВЕЛЬЕВ И.В | |||
| Курс общей физики | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| - М.: Наука, 1978 | |||
| Демонстрационный эксперимент по физике в средней школе | |||
| Ч | |||
| II | |||
| Под ред | |||
| Покровского | |||
| - М.: Просвещение, 1979 | |||
| УЧЕБНЫЙ ОПТИЧЕСКИЙ ИНТЕРФЕРОМЕТР | 1998 |
|
RU2154307C2 |
| УЧЕБНЫЙ ПРИБОР ПО ОПТИКЕ | 1996 |
|
RU2114462C1 |
| US 4493555 C1, 15.01.1985 | |||
| СЫРЬЕВАЯ СМЕСЬ ДЛЯ ИЗГОТОВЛЕНИЯ КОНСТРУКТИВНОГО ТЕПЛОИЗОЛЯЦИОННОГО ПЕНОБЕТОНА | 2003 |
|
RU2237041C1 |
Авторы
Даты
2003-06-10—Публикация
2001-06-29—Подача