Изобретение относится к космической технике, преимущественно к орбитальным тросовым системам.
Орбитальная тросовая система в общем случае представляет собой совокупность Искусственных космических объектов, соединенных длинными тонкими гибкими элементами (тросами, кабелями, шлангами и т.п.), совершающую орбитальное движение. В простейшем и наиболее часто рассматриваемой случае орбитальная тросовая система представляет собой тросовую связку двух космических объектов. Длина троса в такой связке может достигать десятков и сотен километров. При невозмущенном движении по круговой орбите такая связка имеет устойчивое положение, в котором связка вытянута по местной вертикали.
Орбитальные тросовые системы в отличие от обычных космических аппаратов обладают следующими особенностями: очень большой протяженностью, гибко изменяемой конфигурацией, способностью активно взаимодействовать с окружающей средой. Эти особенности орбитальных тросовых систем позволяют в будущем эффективно использовать их для решения в космосе таких задач, которые невозможно, нецелесообразно или неэкономично решать с помощью существующих космических аппаратов.
В частности, орбитальные тросовые системы могут использоваться в качестве протяженных измерительных систем, например, космических интерферометров с очень большой базой. Орбитальные тросовые системы с размещенными вдоль троса датчиками могут использоваться, например, для исследования геофизических полей и околоземной космической среды с проведением синхронных измерений на нескольких различных высотах. Орбитальные тросовые системы с атмосферными зондами могут использоваться для длительных исследований земной атмосферы на высотах 90-120 км, для проведения экспериментов с аэродинамическими моделями, низковысотной фотосъемки поверхности Земли.
Под действием гравитационных и центробежных сил на борту космических объектов, входящих в состав орбитальной тросовой системы, может возникать малая искусственная тяжесть. Этот эффект может быть использован для проведения различных медицинских, биологических, технологических и других экспериментов в условиях малой тяжести, уровень которой можно регулировать. Искусственная тяжесть, возникающая в орбитальной тросовой системе, может использоваться при создании комфортных условий для жизни и работы космонавтов, для выращивания в космосе растений, для дозаправки космических аппаратов топливом и т. п.
Орбитальные тросовые системы могут также использоваться для выполнения различных орбитальных маневров космических объектов без затрат топлива или с уменьшенными затратами топлива. Путем простого отделения объекта от троса в статической, раскачивающейся или быстро вращающейся связке можно сообщить этому объекту достаточно большую дополнительную скорость. Таким образом можно осуществить перевод объекта на высшую или низшую орбиту, его спуск на Землю или даже перевод на траекторию межпланетного полета. Определенным образом изменяя длину троса в связке, можно осуществлять медленные эволюции параметров ее орбиты, а также взаимное маневрирование объектов, входящих в связку.
Орбитальная тросовая система с электропроводным тросом способна осуществлять активное электродинамическое взаимодействие с магнитным полем и ионосферой Земли. Используя эффекты такого взаимодействия, можно получать электроэнергию за счет снижения орбиты связки ("генераторный режим") или повышать орбиту связки за счет расхода электроэнергии ("двигательный режим"). Определенным образом регулируя электрический ток в тросе, можно изменять отдельные параметры орбиты связки. При пропускании в тросе переменного тока орбитальная тросовая система способна эффективно излучать радиоволны сверхнизкочастотного диапазона, что позволяет использовать такую систему в качестве передающей антенны в космической связи.
Развертывание орбитальной тросовой системы на орбите является самостоятельной задачей, техническое решение которой может быть достигнуто различными способами. Все известные способы развертывания связки двух космических объектов основаны на следующей общей схеме. В исходном состоянии два объекта, соединенных тросом, состыкованы друг с другом, а трос компактно уложен. В начальный момент времени объекты расстыковываются и одному из объектов или обоим объектам сообщают начальную скорость расхождения, например, с помощью пружинных толкателей. После этого объекты осуществляют взаимное расхождение, во время которого производится выпуск соединяющего их троса. Выпуск троса может осуществляться в неуправляемом или управляемом режиме с помощью различных устройств: простых невращающихся катушек или же лебедок с электроприводом, способных регулировать скорость выпуска троса, силу его натяжения и т. п. В процессе расхождения с выпуском троса объектам могут сообщаться дополнительные скорости, например, с помощью реактивных двигателей. Целью развертывания орбитальной тросовой системы является, как правило, ее приведение в устойчивое вертикальное положение.
Известны способы развертывания орбитальных тросовых систем, предусматривающие неуправляемый выпуск троса в процессе расхождения объектов. При этом трос обычно выпускается с помощью невращающейся ("безынерционной") катушки, которая должна обеспечивать упорядоченный выход троса с небольшим сопротивлением. Такие способы развертывания использовались в следующих космических экспериментах с орбитальными тросовыми системами:
- в двух американских космических экспериментах с кораблями "Джемини" и ракетной ступенью "Аджена", соединенных синтетической лентой длиной 30 м в 1966 г. [1];
- в четырех американо-японских экспериментах на зондирующих ракетах с полезными грузами массой 75 кг, отводимыми на электропроводных тросах длиной 400 м в 1981-1985 г. [2];
- в двух канадских экспериментах на зондирующих ракетах с полезными грузами массой 100 кг, отводимыми на электропроводных тросах длиной 958 М OEDIPUS-A в 1989 г. и OEDIPUS-C в 1995 г. [3];
- в американском эксперименте SEDS-1 на ракете "Дельта-2" с полезным грузом массой 25 кг, отводимым на полиэтиленовом тросе длиной 20 км в 1993 г. [4];
- в американском эксперименте PMG на ракете "Дельта-2" с полезным грузом, отводимым на тросе длиной 500 м в 1993 г. [5].
Неуправляемый выпуск троса придает процессу развертывания орбитальной тросовой системы случайный и неустойчивый характер, что может воспрепятствовать достижению заданного конечного положения связки. Так, в первых двух американо-японских экспериментах фактическое сопротивление выходу троса существенно превышало расчетную величину, вследствие этого в первом эксперименте трос был выпущен всего на 30 м, а во втором эксперименте - на 60 м вместо предполагавшихся 400 м. В эксперименте SEDS-1 фактическое сопротивление выходу троса было намного меньше расчетной величины, что привело к рывку и разрыву троса в конце развертывания вследствие слишком большой скорости отхода полезного груза.
Известны способы развертывания орбитальных тросовых систем, предусматривающие выпуск троса с регулированием скорости его выпуска. При выпуске троса с постоянной скоростью реализуется так называемое "равномерное" развертывание, а при выпуске троса со скоростью, пропорциональной длине его выпущенной части, - так называемое "экспоненциальное" развертывание. Известны также многочисленные модификации такого способа развертывания, когда скорость выпуска троса регулируется в зависимости от длины его выпущенной части и в соответствии с заданным угловым движением связки относительно местной вертикали. Описание и анализ различных способов развертывания орбитальных тросовых систем с регулированием скорости выпуска троса имеются в источниках [6-17].
Способ развертывания орбитальной тросовой системы с регулированием скорости выпуска троса использовался в американо- итальянских космических экспериментах на корабле "Спейс Шаттл" с привязным спутником массой 500 кг, отводимым на электропроводном тросе длиной 20 км: в эксперименте TSS-1 в 1992 г. [18] и в эксперименте TSS-1R в 1996 г. [19]. Выпуск троса в этих экспериментах осуществлялся с помощью сложной лебедки ("The Deployer"), состоящей из барабана с намотанным тросом, автоматизированного электропривода, двух вытягивающих роликовых механизмов и выдвижной фермы. Привязной спутник был снабжен реактивными двигателями для разгона спутника в начале его отведения.
Все способы развертывания орбитальных тросовых систем с регулированием скорости выпуска троса имеют один общий недостаток. При таком управлении выпуском троса невозможно осуществить гашение продольных колебаний связки, возникающих вследствие упругости троса. Увеличение интенсивности продольных колебаний способно привести к полному ослаблению троса, что в свою очередь может вызвать перебои в работе устройств выпуска троса. По-видимому, этот недостаток явился причиной неудачного развертывания орбитальных тросовых систем в экспериментах TSS-1 и TSS-1R. В эксперименте TSS-1 трос был выпущен на длину 265 м, после чего произошло его заедание в механизмах выпуска. В эксперименте TSS-1R трос удалось выпустить почти полностью, но в самом конце развертывания произошел разрыв троса в месте его выхода из механизмов выпуска.
Известны способы развертывания орбитальных тросовых систем, предусматривающие выпуск троса с регулированием силы его натяжения. Основным преимуществом таких способов развертывания является возможность непосредственного гашения продольных колебаний связки в процессе выпуска троса. Описание таких способов развертывания и устройств для их реализации имеется в источниках [20-24] . Способ развертывания орбитальной тросовой системы с регулированием силы натяжения троса использовался в американском космическом эксперименте SEDS-2 на ракете "Дельта-2" с полезным грузом, отводимым на тросе длиной 20 км в 1994 г. [25].
Е. М. Левиным был предложен способ развертывания орбитальной тросовой системы с регулированием силы натяжения троса пропорционально длине его выпущенной части [9,26]. Подробный анализ этого способа развертывания имеется в источниках [6,8]. В частности, показано, что при определенных условиях этот способ позволяет осуществить в процессе развертывания так называемое вертикальное расхождение ("вертикальный дрейф") соединенных тросом объектов по прямолинейным траекториям, параллельным местной вертикали, с постоянной скоростью. Недостатком этого способа является высокая чувствительность процесса развертывания к реальным ошибкам в обеспечении начальных условий и погрешностям регулирования силы натяжения выпускаемого троса.
Наиболее близким аналогом изобретения является способ развертывания орбитальной тросовой системы, описание которого имеется в источнике [27]. Описанный в этом источнике способ предусматривает развертывание орбитальной тросовой системы в три этапа: выведение объектов на траекторию вертикального расхождения, вертикальное расхождение объектов и приведение связки к местной вертикали. На разных этапах развертывания используются различные законы регулирования силы натяжения троса в зависимости от текущей длины его выпущенной части и скорости выпуска, причем для каждого закона зависимость заданной силы натяжения троса от его длины и скорости выпуска является линейной.
Этот способ заключается в следующем. В исходном состоянии два соединенных тросом объекта ("основной спутник" и "субспутник") состыкованы друг с другом, а трос компактно уложен ("намотан на лебедку"). В начальный момент времени t = 0 одному объекту сообщается начальная скорость V0 относительно другого объекта, направленная вдоль местной вертикали. Затем выпускается трос с регулированием силы его натяжения по закону, формируемому в соответствии с данными о длине и скорости выпуска троса. Трос выпускается до достижения его конечной длины и установки системы вдоль местной вертикали.
На первом этапе развертывания сила натяжения троса регулируется в соответствии с законом, выражаемым формулой: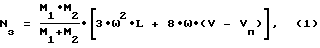
где
N3 - заданная сила натяжения троса;
M1 и M2 - масса первого и второго объекта соответственно: ω - - средняя угловая скорость орбитального движения системы;
L - длина выпущенной части троса;
V - фактическая скорость выпуска троса;
VП- программная скорость выпуска троса, определяемая по формуле: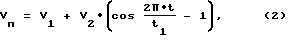
где
V1 = 0,9•V0, V2 = 0,3•V1, t1 = 0,7/ω . Этот закон регулирования силы натяжения троса обеспечивает выведение объектов на траекторию вертикального расхождения.
В момент времени t = t1 осуществляется переход на второй этап развертывания, на котором сила натяжения троса регулируется по закону, также выражаемому формулой (1), в которой программная скорость VП = V1. Этот закон регулирования силы натяжения троса обеспечивает вертикальное расхождение объектов по траекториям, асимптотически приближающимся к прямым линиям, параллельным местной вертикали.
В момент времени t = t2, определяемый из условия непрерывности управления, осуществляется переход на третий этап развертывания, на котором сила натяжения троса регулируется по закону, выражаемому формулой: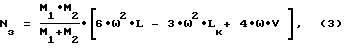
где
LК - номинальная длина троса в развернутой системе. Этот закон регулирования силы натяжения троса обеспечивает максимально быстрое гашение остаточных колебаний системы в плоскости орбиты и ее установку в вертикальное положение с конечной длиной троса, близкой к номинальной.
Недостатком способа, принятого в качестве прототипа, является сложность практической реализации развертывания орбитальной тросовой системы, связанная со сложным алгоритмом регулирования силы натяжения выпускаемого троса. Развертывание орбитальной тросовой системы осуществляется в три этапа, на каждом из которых используются различные законы регулирования силы натяжения троса. При выпуске троса используется управление силой натяжения троса не только по фазовым переменным (длине и скорости выпуска троса), но и по времени. Для выпуска троса при таком развертывании потребуется сложное устройство, снабженное системой датчиков, вычислительными и логическими схемами и автоматизированным приводом-регулятором.
Изобретение направлено на решение технической задачи развертывания орбитальной тросовой системы, предусматривающее простоту практической реализации развертывания. Это достигается за счет упрощения алгоритма регулирования силы натяжения выпускаемого троса.
Сущность изобретения заключается в том, что два соединенных тросом объекта расстыковывают и по крайней мере одному объекту сообщают относительную скорость расхождения вдоль местной вертикали. Затем выпускают трос, регулируя силу его натяжения в зависимости от длины его выпущенной части и скорости выпуска.
В отличие от прототипа силу натяжения троса регулируют по закону
N3=A•V/1-B•L/Lk,
где
N3 - заданная сила натяжения троса;
V - скорость выпуска троса;
L - текущая длина выпущенной части троса;
LК - заданная конечная длина троса в развернутой системе;
A и B - постоянные положительные величины, причем B меньше единицы. В отличие от прототипа выпуск троса прекращают в момент, когда длина выпущенной части троса станет равной заданной конечной длине троса.
Сущность изобретения поясняется чертежом.
Процесс развертывания орбитальной тросовой системы описывается в орбитальной системе координат XOY, где центр O совпадает с центром масс одного ("верхнего") объекта, ось Y направлена вниз по местной вертикали, а ось X лежит в плоскости орбиты и направлена перпендикулярно оси Y вперед по направлению полета системы. Система движется по околокруговой орбите. В исходном состоянии объекты состыкованы, а трос компактно уложен. В процессе развертывания системы "нижний" объект движется относительно "верхнего" объекта, описывая траекторию в координатах XOY.
В начальный момент времени объекты расстыковывают и одному из объектов или обоим объектам, например, с помощью пружинных толкателей и/или реактивных двигателей, сообщают начальную скорость взаимного расхождения, направленную вдоль местной вертикали, т.е. по оси Y. Затем выпускают трос, регулируя силу его натяжения N таким образом, чтобы она поддерживалась на уровне заданной величины N3, определяемой по формуле (4). Величины A и B в формуле (4) можно задать, исходя из условий точности приведения орбитальной тросовой системы к устойчивому вертикальному положению, допустимости остаточных колебаний системы после развертывания и требуемой длительности развертывания. Выпуск троса прекращают в момент, когда длина выпущенной части троса L достигнет заданной конечной длины троса LК.
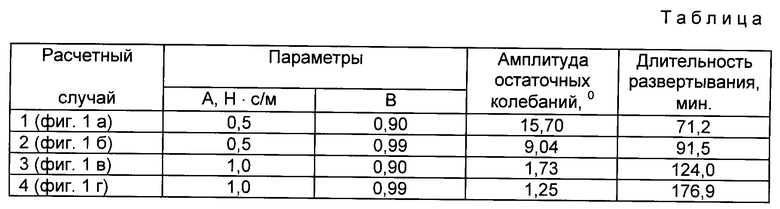
На чертеже показаны расчетные траектории движения "нижнего" объекта относительно "верхнего" объекта в процессе развертывания орбитальной тросовой системы. Расчет проводился для следующих параметров: масса "верхнего" объекта 5000кг, масса "нижнего" объекта 250 кг, средняя угловая скорость орбитального движения системы 0,001 рад/с, заданная конечная длина троса 1000 м, начальная скорость расхождения объектов 0,5 м/с. В таблице приведены исходные данные и расчетные параметры, соответствующие четырем расчетным случаям, показанным на чертеже. Из таблицы видно, что увеличение значений коэффициентов A и B приводит к улучшению точности приведения системы к устойчивому вертикальному положению, но при этом развертывание становится более длительным.
Список литературы
1. Lang D. D., Nolting R.R. Operations with tethered space vehicles // Gemini Summary Conference, February 1-2, 1967, Houston, Texas, NASA SP-138. - P. 55-66.
2. Sasaki S., Oyama K.I., Kawashima N. et al. Results from a series of tethered rocket experiments // Journal of Spacecraft and Rockets. - 1987. - V. 24, N 5. - P. 444-453.
3. Tyc G., Vigneron F.R., Jablonski A.M. Tether dynamics investigations for the Canadian OEDIPUS and BICEPS missions // International Round Table on Tethers in Space. - ESTEC, Noordwijk, The Netherlands. - 28-30 September 1994.
4. Bergamaschi S., Loria A., Wood G.M. SEDS-I features and dynamics during deployment // International Round Table on Tethers in Space. - ESTEC, Noordwijk, The Netherlands. - 28-30 September 1994.
5. Chlouber D., Jost R. 3., McCoy 3. E., Wilson T. L. Plasma Motor Generator (PMG) mission report // Houston, Texas, NASA JSC-26714.- August 15, 1984.
6. Белецкий B.B., Левин E. M. Динамика космических тросовых систем. - M: Наука, 1990.
7. Иванов В. А. , Лаптырев Д. А. Исследование относительного движения связки двух космических объектов при регулировании длины троса // Космические исследования. - 1986. - T. XXIV, вып. 4. - с. 544-552.
8. Иванов В.А., Ситарский Ю.С. Динамика полета системы гибко связанных космических объектов. - M: Машиностроение, 1986.
9. Левин E. M. О развертывании протяженной связки на орбите // Космические исследования. - 1983. - T. XXI, вып. l. - с. 678-688.
10. Eades J.В.J. Analytical solution for extensible tethers // Journal of Spacecraft and Rockets. - 1974. - V. II. - N 4. - P. 254- 255.
11. Kane T. R., Levinson D.A. Deployment of a cable- supported payload from an orbiting spacecraft // Journal of Spacecraft and Rockets. - 1977. - V. 14.- N 7. - P. 409-413.
12. Misra A. K., Modi V. 3. Deployment and retrieval of a subsatellite connected by a tether to the Space Shuttle // AIAA Paper. - 1980. - N 1693. - 9 p.
13. Misra A. K. , Modi V. 3. Deployment and retrieval of Shuttle supported tethered satellites // Journal of Guidance, Control and Dynamics. - 1982. - V. 5.- N 3. - P. 278-285.
14. Modi V.3., Misra A.K. Deployment dynamics and control of the Space Shuttle based tethered subsatellite systems // Proceedings of 13 International Symposium on Space Technology and Science. - Journal of Astronautical Sciences. - 1983. - V. 31. - N l. - P. 135-149.
15. Modi V. 3. , Misra A.K. Deployment dynamics of tethered satellite systems // AIAA Paper. - 1978. - N 1398. - P. lO
16. Modi V.3., Misra A.K. On the deployment dynamics of tether connected two-body systems // Journal of the Academy of Astronautics. - 1979. - V. 6.- P. 1179-1183.
17. Von Flotow A.H., Williamson P.R. Deployment of a tethered satellite pair into low earth orbit for plasma diagnostics // Journal of the Astronautical Sciences. - 1986. - V. 34. - N l. - P. 65-90.
18. Space Shuttle mission STS-46 press kit. NASA, July 1992.
19. The Tethered Satellite System Reflight. NASA, February 1996.
20. Eades J. B. J. A control system for orbiting tethered- body operations // Proceedings IFAC 6-th World Congress. - Boston- Cambriedge. - 1975. - Part. 4. - Pittsburgh. - 1975, 14.2/1 - 14.2/6.
21. Rupp C.C., Kissel R.R. Tetherline system for orbiting satellites. U. S. Patent N 4083520, April II, 1978, Int. Cl. B. 64 G 1/100, US Cl. 244/167; 244/161.
22. Rupp C. C., Laue 3. H. Shuttle/Tethered Satellite System // Journal of Astronautical Sciences. - January-March 1978. - V. XXVI. -NI. -P. 1-17.
23. Swet C. J. Method for deployment and stabilising orbiting structures. U.S. Patent Office N 3532298, Oct. 6, 1970, Int. Cl. B 64 G 1/00, U.S. Cl. 244-1.
24. Swet C. J., Whisnant 3. M. Deployment of a tethered orbiting interferometer // Journal of Astronautical Sciences. - July- August, 1969. - V. XVII. -N 1. - P. 44-59.
25. Wood G.M. et al. The Small Expendable Deployer System (SEDS) end mass experiments // International Round Table on Tethers in Space. - ESTEC, Noordwijk, The Netherlands, 28-30 September 1994.
26. Левин E. M. Динамика орбитальной тросовой системы: Автореф. дис. канд. физ.-мат. наук / МГУ, М., 1983.
27. Левин E. M. Метод выделения быстрых и медленных составляющих управляемых движений орбитальных тросовых систем // Техническая кибернетика, 1991, N 2, с.195-199.
Изобретение относится к космической технике и касается процесса развертывания на орбите тросовой системы в виде связки двух объектов обеспечением простоты реализации процесса, в начале которого два соединенных тросом объекта расстыковывают и хотя бы одному из них сообщают скорость расхождения вдоль местной вертикали, после чего выпускают трос, регулируя силу его натяжения по закону N3=A•V/(1-B•L/Lк), где N3 - заданная сила натяжения троса. V - скорость выпуска троса; L - текущая длина выпущенной части троса, Lк заданная конечная длина троса, А и В - постоянные положительные величины, причем В меньше единицы. Выпуск троса прекращают в момент, когда его длина станет равной заданной конечной. 1 табл., 1 ил.
Способ развертывания орбитальной тросовой системы, включающий расстыковку двух соединенных тросом объектов, сообщение по крайней мере одному объекту начальной скорости расхождения вдоль местной вертикали и выпуск троса с регулированием силы его натяжения, отличающийся тем, что силу натяжения троса регулируют по закону
N3 = (A • V)/(I - B • L/Lк),
где N3 - заданная сила натяжения троса;
V - скорость выпуска троса;
L - текущая длина выпущенной части троса;
Lк - заданная конечная длина троса;
A и B - положительные постоянные величины, выбираемые из требования заданных точности и длительности развертывания тросовой системы и устойчивое вертикальное положение, причем B меньше единицы;
выпуск троса прекращают в момент, когда длина выпущенной части троса станет равной заданной конечной длине троса.
Авторы
Даты
1998-06-10—Публикация
1996-10-03—Подача